一、线索二叉树的概念
1.1 普通二叉树的局限性
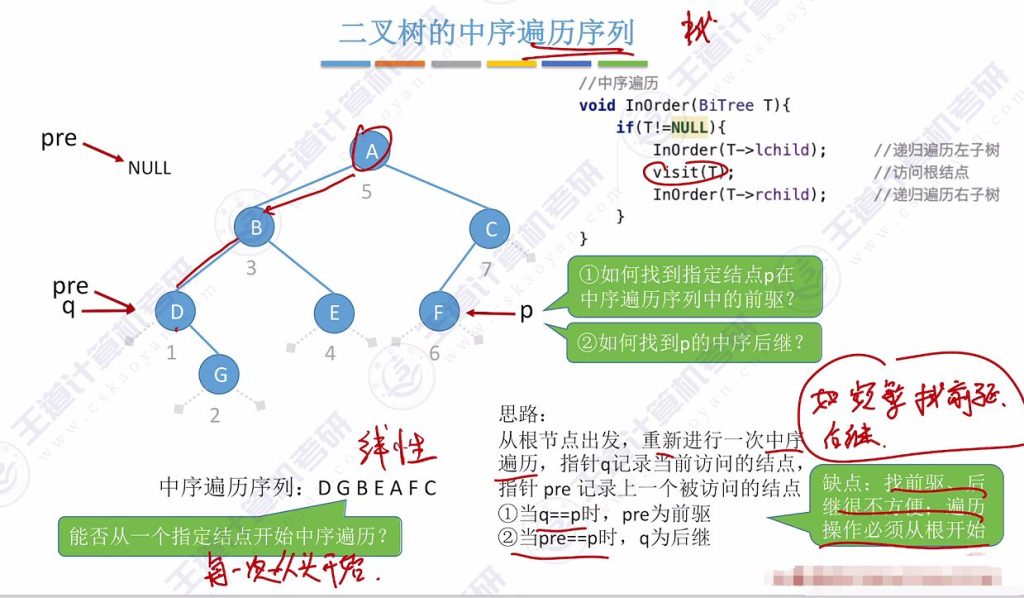
- 遍历起点限制:普通二叉树必须从根节点开始遍历,无法从任意节点开始遍历
- 前驱查找困难:要找到指定节点p的中序前驱,需要从根节点重新进行完整的中序遍历,用指针q记录当前节点,pre记录前驱节点
- 后继查找困难:原理与前驱查找类似,需要完整遍历才能确定后继关系
为什么要有线序二叉树?
需要频繁的访问前驱和后继
1.2 中序线索二叉树
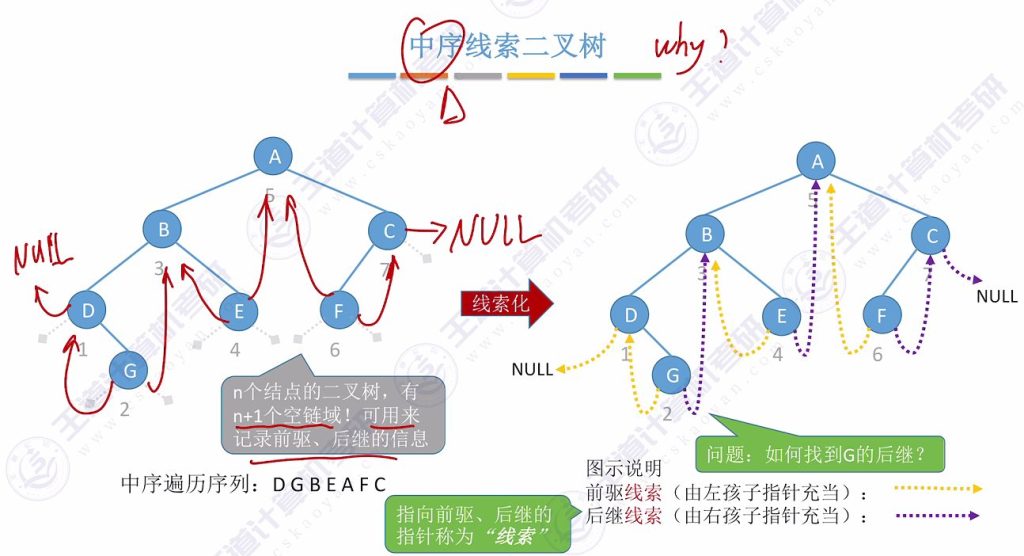
- 利用空链域:n个节点的二叉树有n+1个空链域,可用这些空指针记录前驱后继信息
- 快速查找:通过线索可直接找到任意节点的前驱和后继
- 便利遍历:可以从任意节点开始遍历,只需沿着后继线索即可
1.3 线索二叉树的存储结构
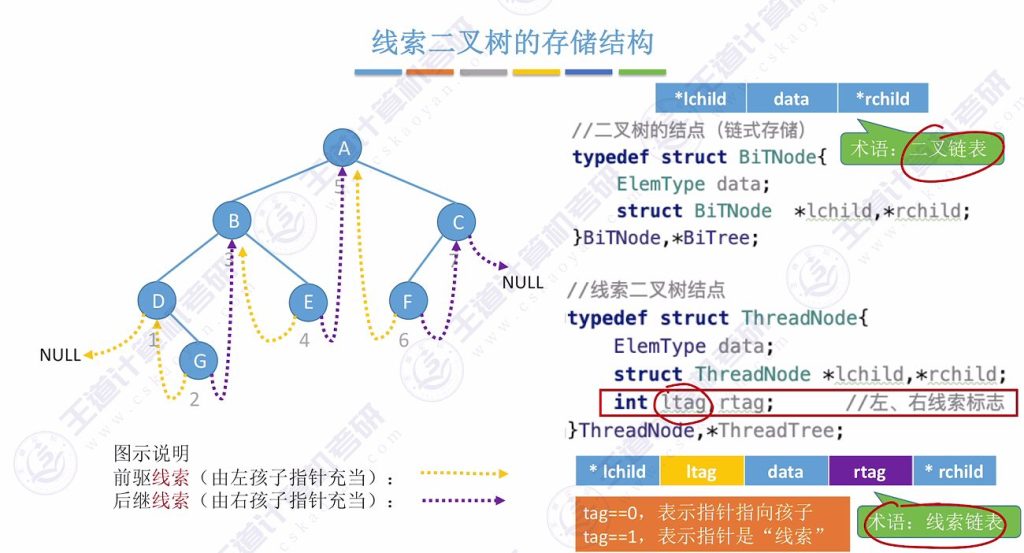
普通二叉树称为”二叉链表”
线索二叉树称为”线索链表”
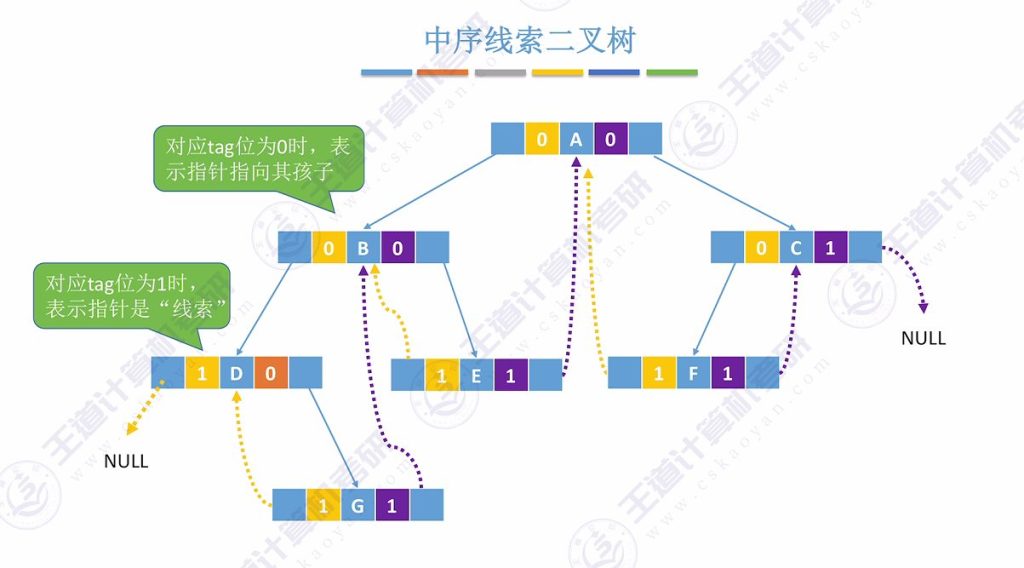
1.4 中序线索二叉树的存储结构
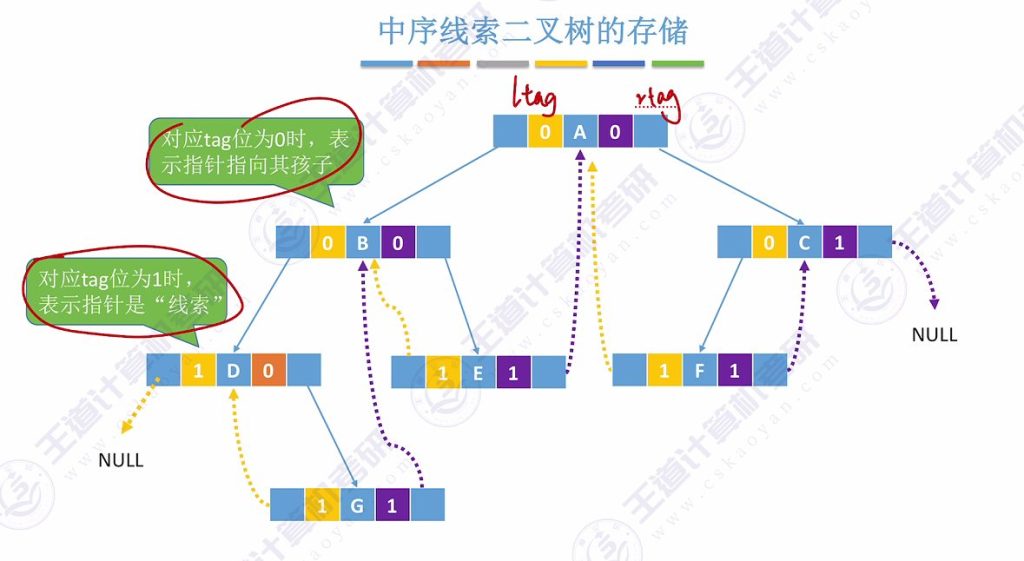
- 存储表示:tag位标记线索状态,1表示线索,0表示孩子指针
1.5 先序线索二叉树
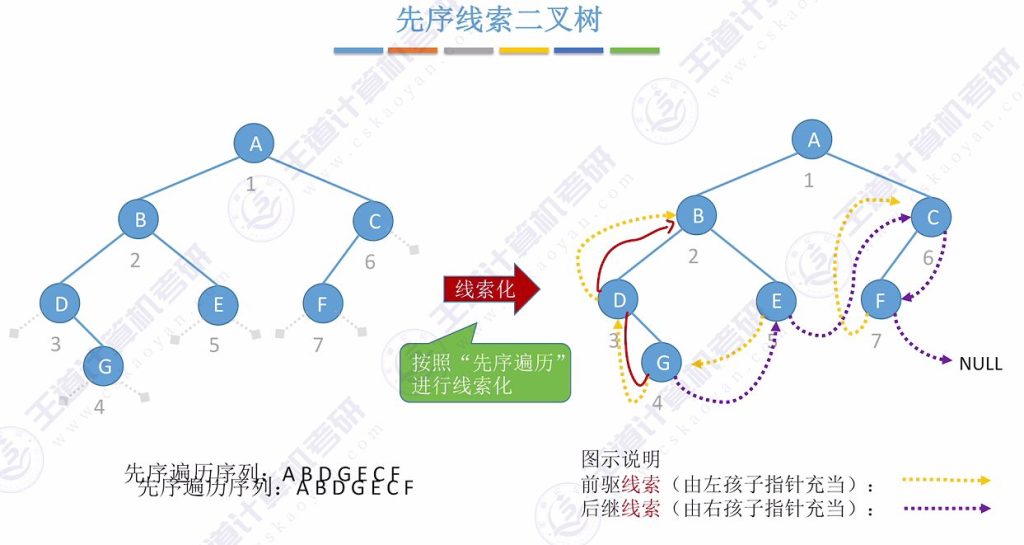
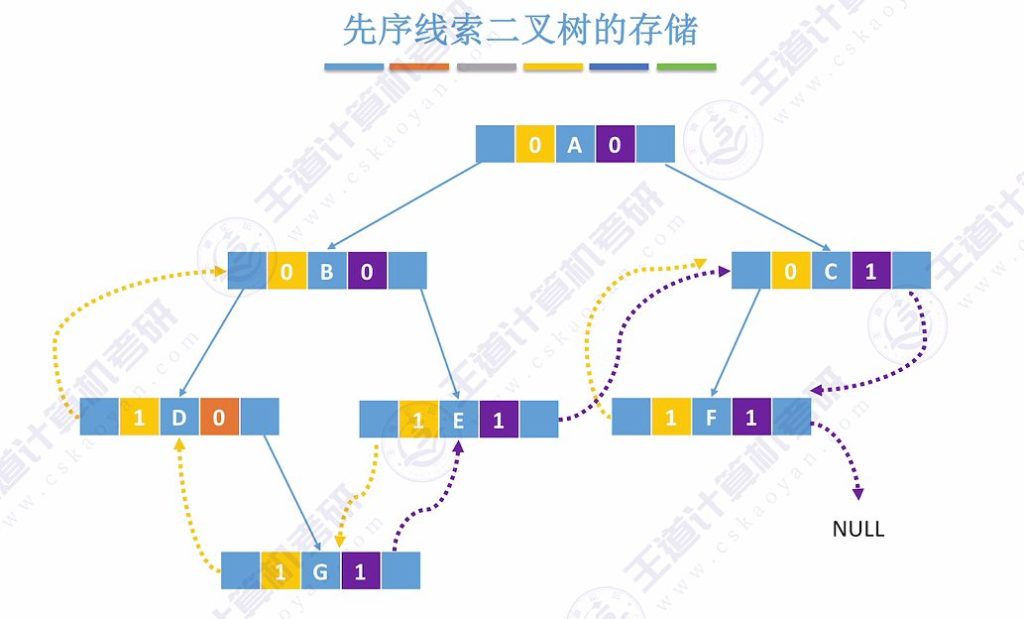
- 构建方法:按照先序遍历序列确定前驱后继关系
- 存储表示:tag位标记线索状态,1表示线索,0表示孩子指针
1.6 后序线索二叉树
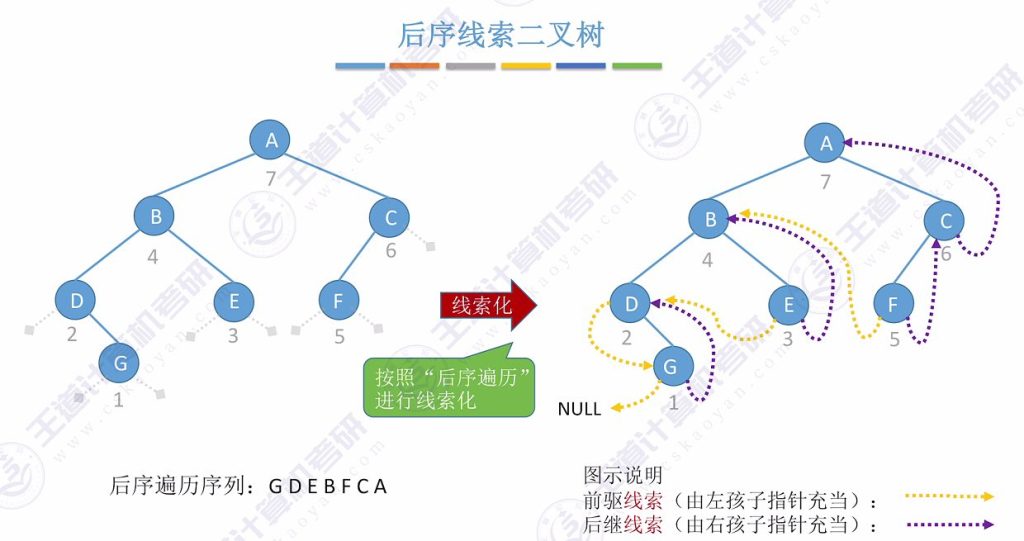
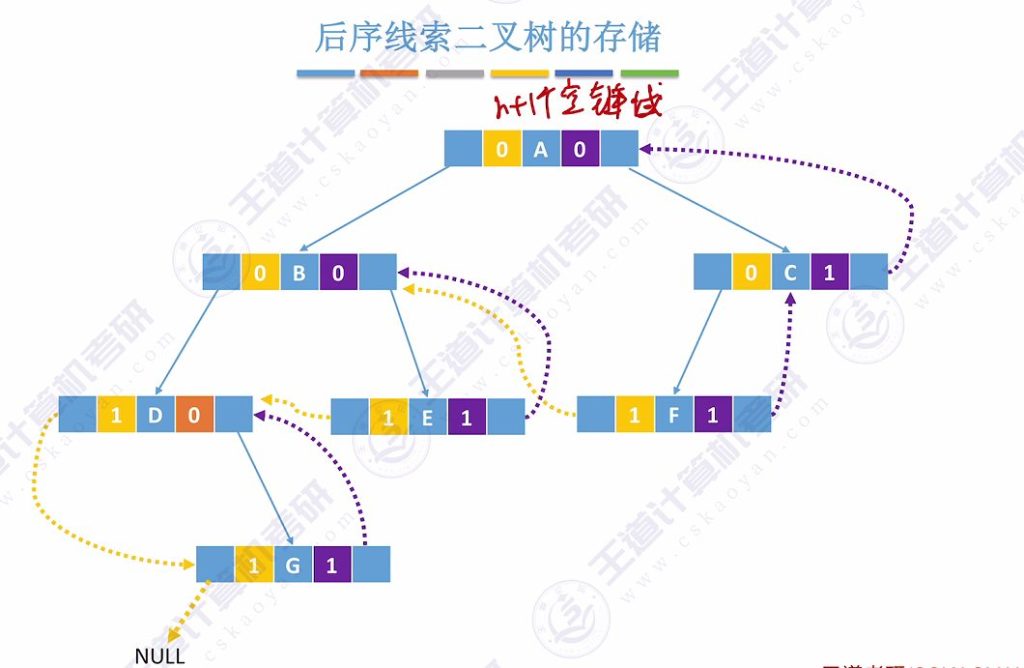
- 构建方法:按照后序遍历序列确定前驱后继关系
- 首节点处理:第一个访问的节点左指针指向NULL
1.7 三种线索二叉树的对比
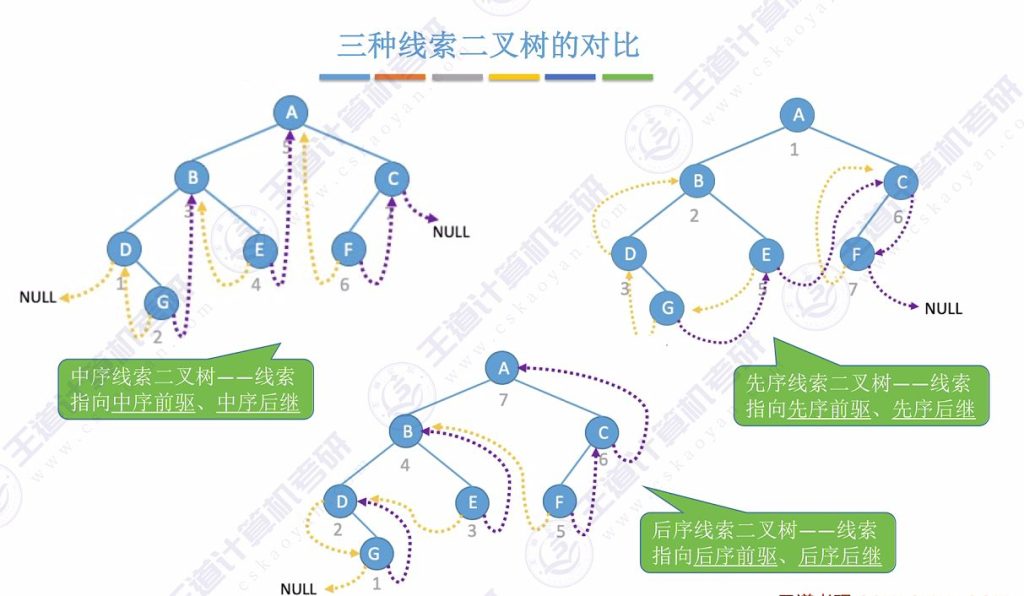
- 区分依据:根据构建时使用的遍历序列类型
- 中序线索二叉树:基于中序遍历序列
- 先序线索二叉树:基于先序遍历序列
- 后序线索二叉树:基于后序遍历序列
- 概念区分:
- 中序前驱/后继:中序遍历序列中的前后关系
- 先序前驱/后继:先序遍历序列中的前后关系
- 后序前驱/后继:后序遍历序列中的前后关系
1.8 知识回顾与重要考点
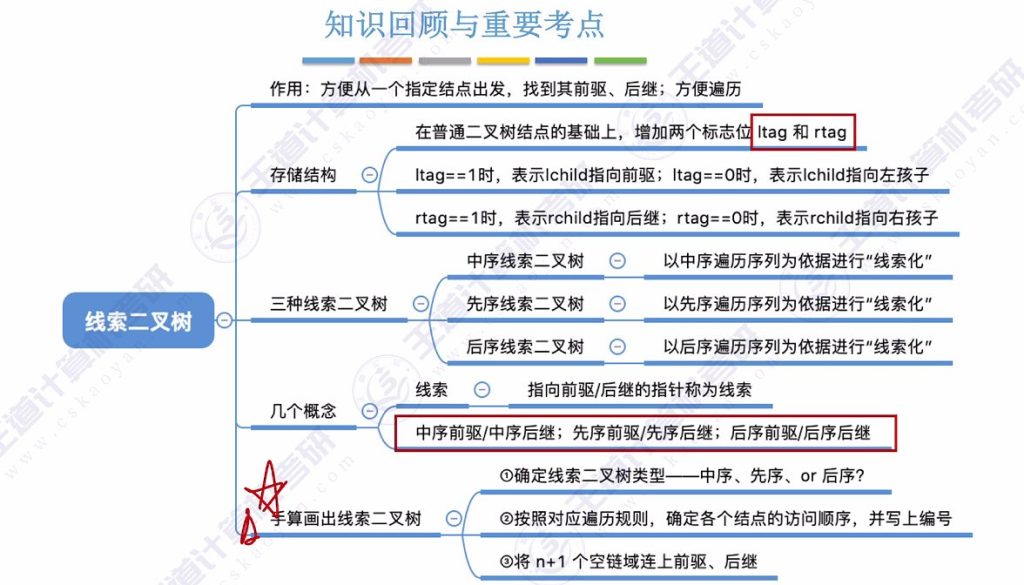
- 核心作用:
- 方便查找任意节点的前驱和后继
- 支持从任意节点开始的遍历
- 存储关键:
- 增加ltag和rtag标志位
- tag=1表示线索,tag=0表示孩子指针
- 手算要点:
- 确定线索二叉树类型(中序/先序/后序)
- 按对应遍历规则确定节点访问顺序并编号
- 将n+1个空链域连上前驱和后继
二、二叉树的线索化
- 三种线索化方式:根据遍历顺序不同分为中序线索化、先序线索化和后序线索化
- 实现本质:都是对相应遍历算法的改造,在访问节点时建立前驱/后继线索
2.1 普通二叉树中序前驱的代码实现
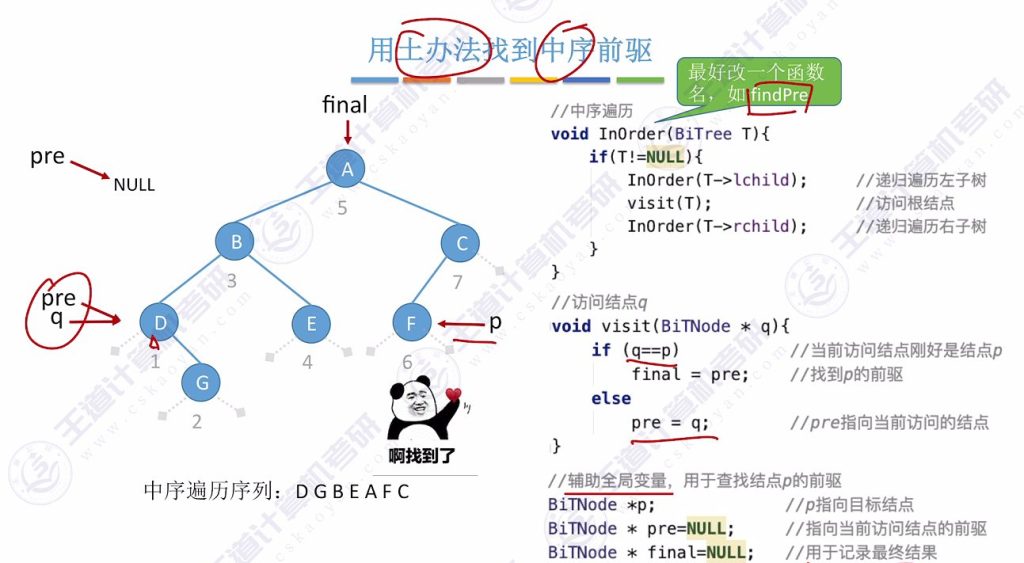
- 核心思想:通过中序遍历整棵树,用pre指针记录前驱节点
- 实现步骤:

- 时间复杂度:O(n),需要完整遍历整棵树
2.2 中序线索化
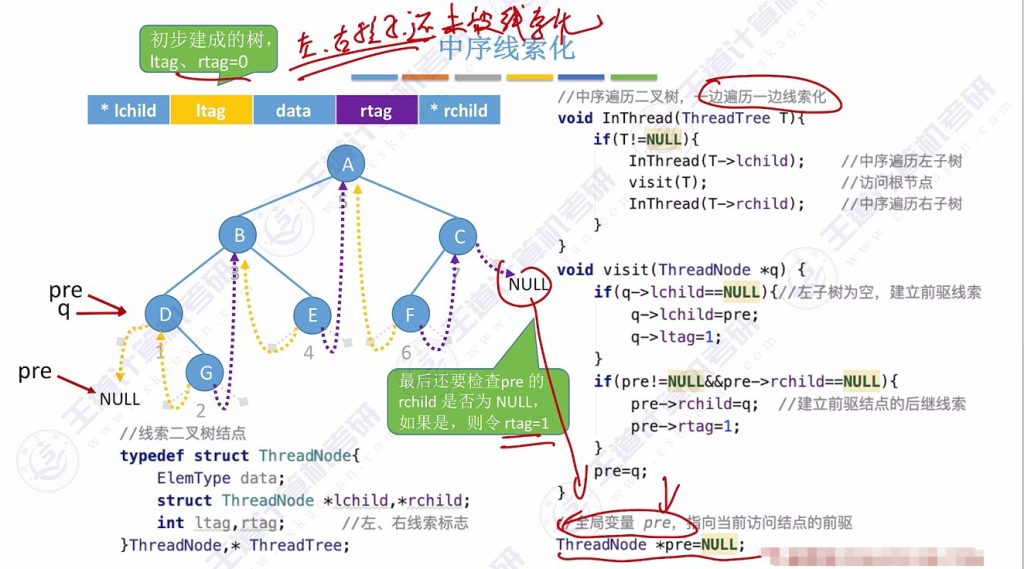

- 节点结构:
- 包含ltag和rtag标志位(0表示孩子,1表示线索)
- 使用ThreadNode结构体存储数据和孩子指针
- 算法流程:
- 中序遍历左子树
- 访问根节点时:
- 若左孩子为空,建立前驱线索指向pre
- 若pre的右孩子为空,建立后继线索指向当前节点
- 中序遍历右子树
- 特殊处理:遍历完成后需检查最后一个节点的右指针,若为空则设置rtag=1
注意:这里的pre是全局变量
2.3 中序线索化王道教材版

- 关键区别:
- 使用引用参数pre替代全局变量
- 最后一个节点处理时直接设rtag=1(因为中序遍历最后一个节点必无右孩子)
- 递归过程:
- 左子树线索化 → 处理当前节点 → 右子树线索化
- 注意事项:引用参数pre确保各层递归共享同一个前驱指针
这里的pre指针是局部变量
2.4 先序线索化
visit(T) 存在问题
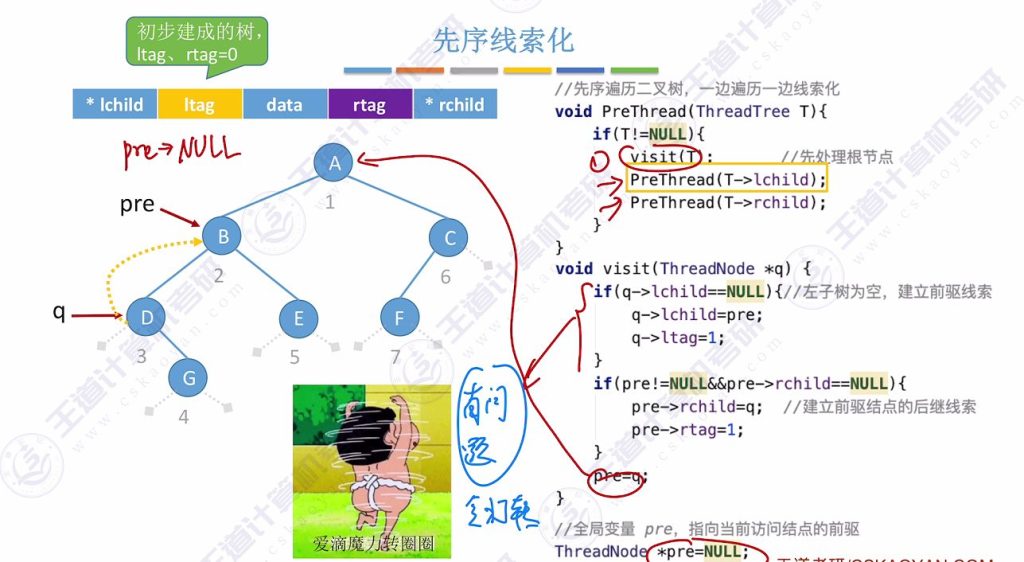
- 核心问题:“爱滴魔力转圈圈”现象
- 原因:线索化后的左指针可能指向前驱,导致无限递归
- 解决方案:
- 添加判断条件:仅当ltag==0ltag==0ltag==0时才递归处理左子树
- 算法特点:
- 访问顺序:根 → 左 → 右
- 必须处理最后一个节点的右指针(可能为空)
解决问题的方法
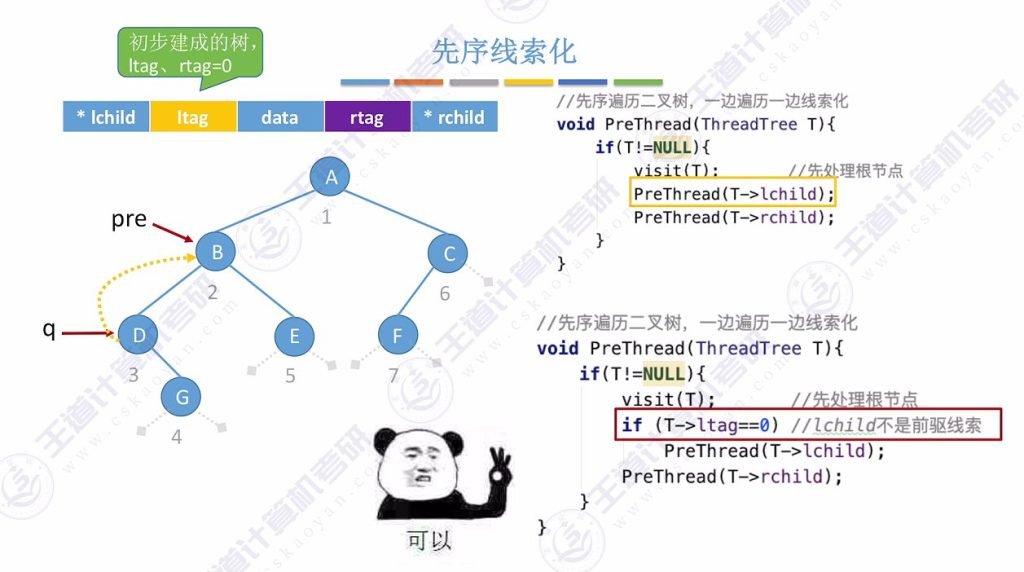
完整版代码

2.5 先序线索化王道教材版

2.6 后序线索化

- 执行顺序:左 → 右 → 根
- 优势:天然避免转圈问题(子树已完全处理)
- 处理逻辑:
- 左子树线索化 → 右子树线索化 → 处理当前节点
- 无需特殊条件判断(类似中序线索化)
2.7 后序线索化王道教材版
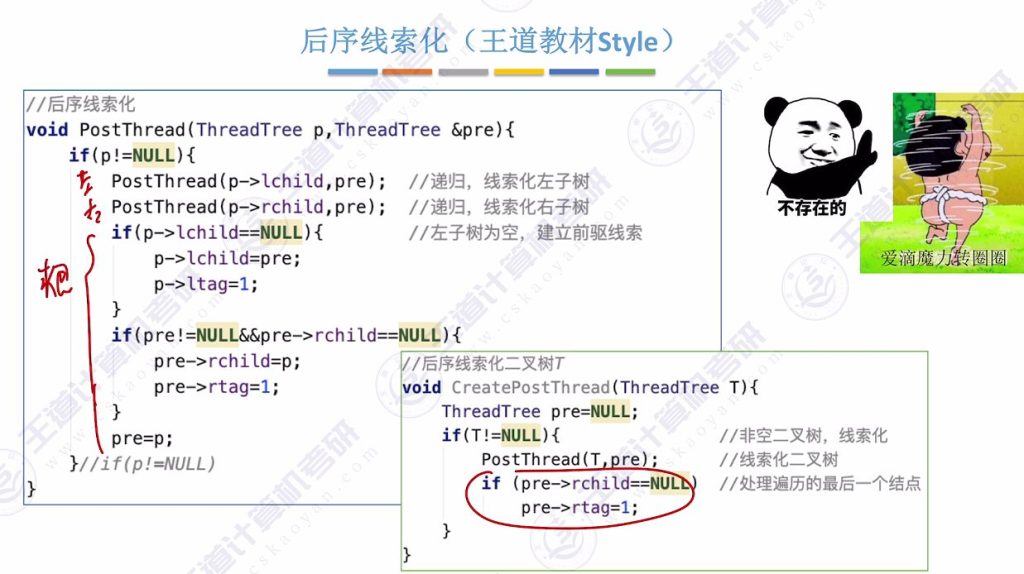
2.8 知识要点

- 核心要点:
- 三种线索化都是对应遍历算法的改造
- 必须用pre指针记录前驱节点
- 最后节点需特殊处理(rtag=1)
- 易错点:
- 先序线索化必须检查ltagltagltag避免转圈
- 中序/后序无此问题(子树已处理完成)
- 实现差异:
- 全局变量pre vs 引用参数pre
- 最后一个节点处理方式(判断右指针是否为空)
三、线索二叉树找前驱 / 后继
- 建立初衷:通过线索化更方便地从一个节点找到其前驱或后继节点
- 主要内容:中序、先序、后序三种线索二叉树的前驱/后继查找方法
3.1 中序线索二叉树找中序后继
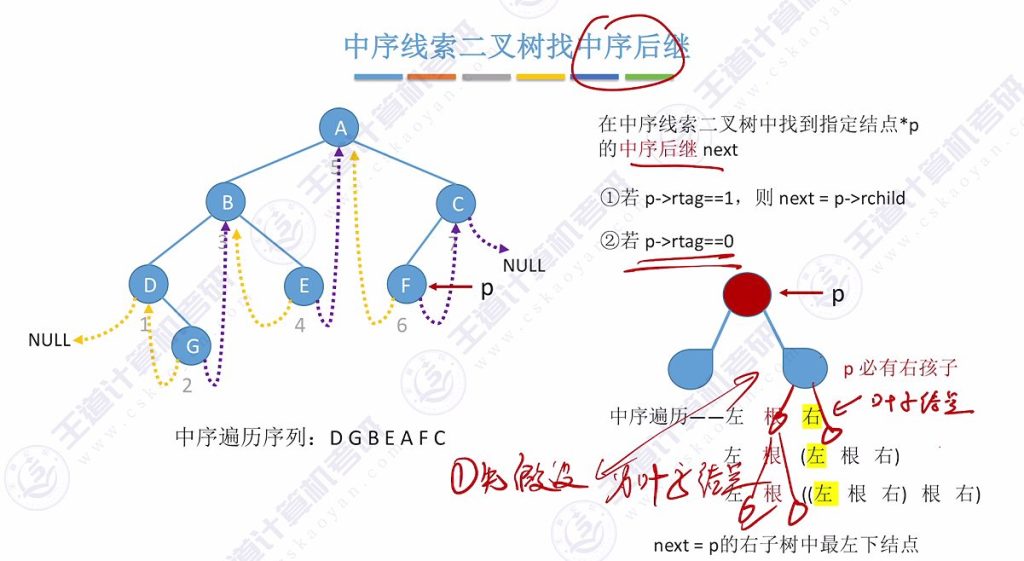
- 右指针线索化情况:当rtag=1时,右指针直接指向中序后继
- 右指针未线索化情况:
- 必有右子树(rtag=0)
- 后继为右子树中最左下角节点
- 示例:若p只有右孩子且为叶子节点,则该右孩子即为后继
3.2 对中序线索二叉树找中序后继(代码)
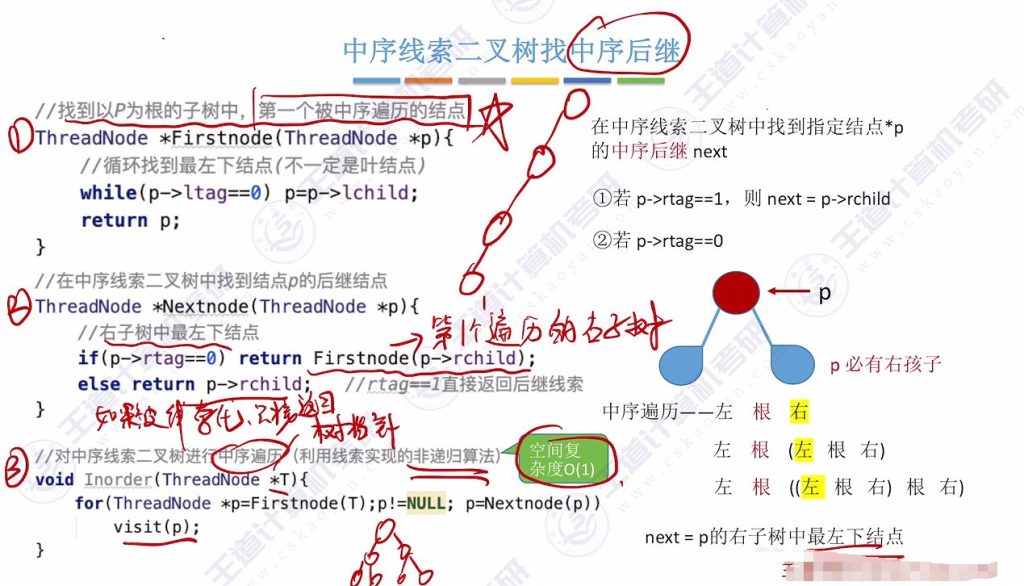
1、找到P为根的子树中,第一个被中序遍历到的结点
Firstnode函数:循环找到子树最左下节点(不一定是叶节点)
2、在中序线索二叉树中找到结点p的后继结点
- Nextnode函数:
- rtag=0时返回右子树的Firstnode
- rtag=1时直接返回右指针
3、遍历算法:
- 空间复杂度O(1)
- 非递归实现:从Firstnode开始,通过Nextnode依次访问
3.3 中序线索二叉树找中序前驱
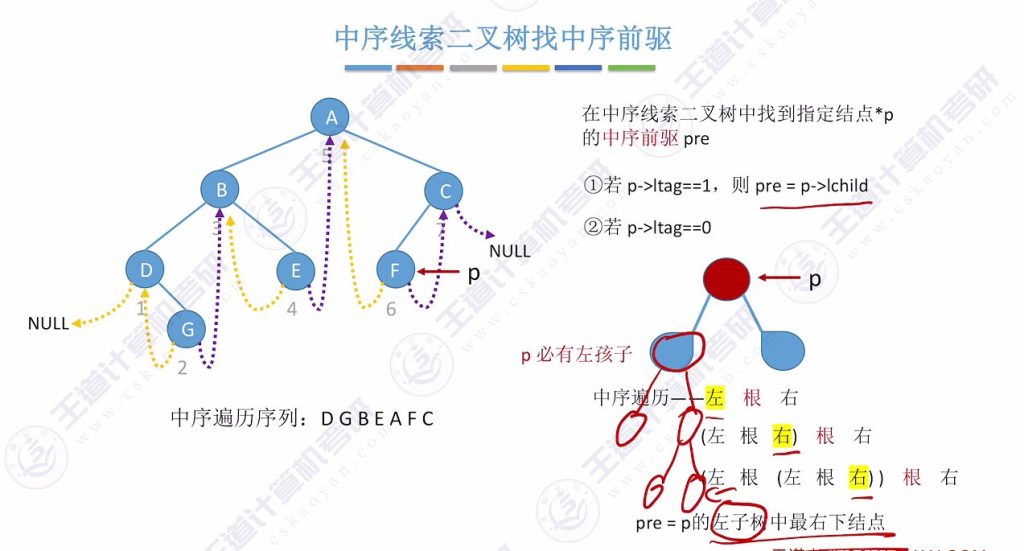
- 左指针线索化情况:当 ltag=1 时,左指针直接指向中序前驱
- 左指针未线索化情况:
- 必有左子树(ltag=0)
- 前驱为左子树中最右下角节点
- 示例:若左子树只有一个节点,则该节点即为前驱
3.4 中序线索二叉树找中序前驱
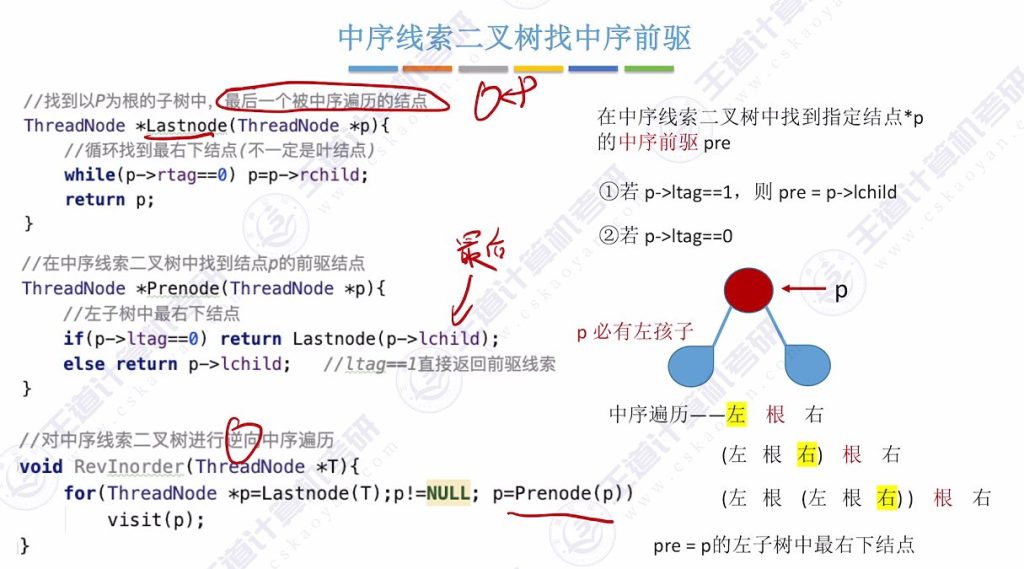
Lastnode函数:循环找到子树最右下节点
逆向遍历
3.5 先序线索二叉树找先序后继
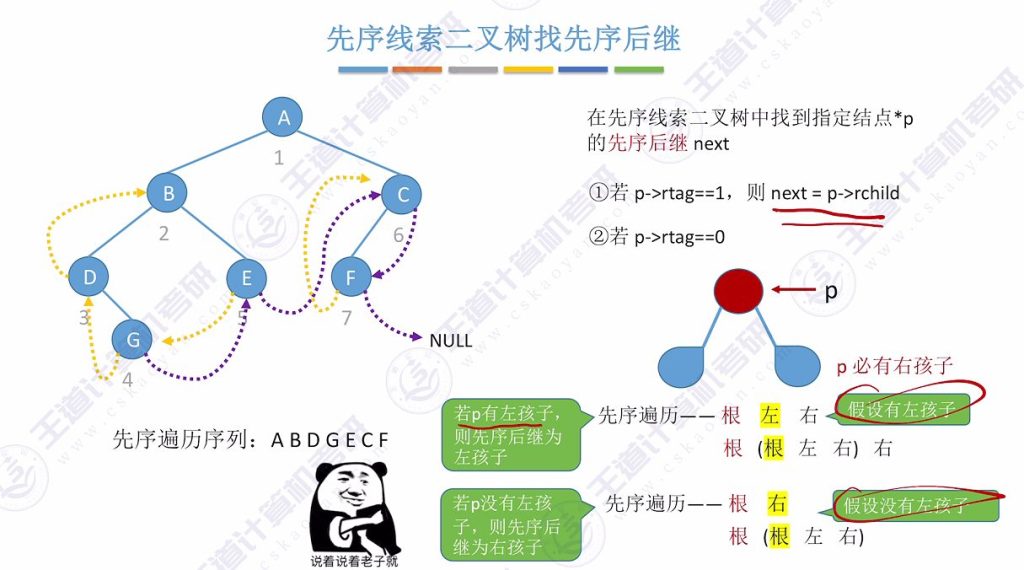
右指针线索化情况:rtag=1时直接返回右指针
- 右指针未线索化情况:
- 有左孩子时:先序后继为左孩子
- 无左孩子时:先序后继为右孩子
- 示例:序列ABDGECF中,B的后继为D,E的后继为C
3.6 先序线索二叉树找先序前驱
找不到先序前驱,除非土办法遍历
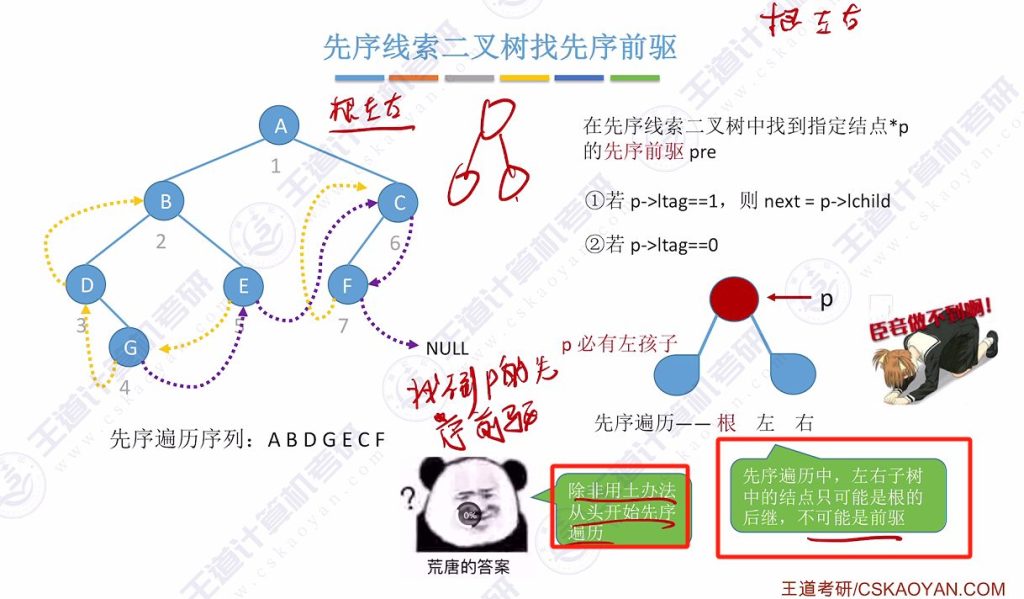
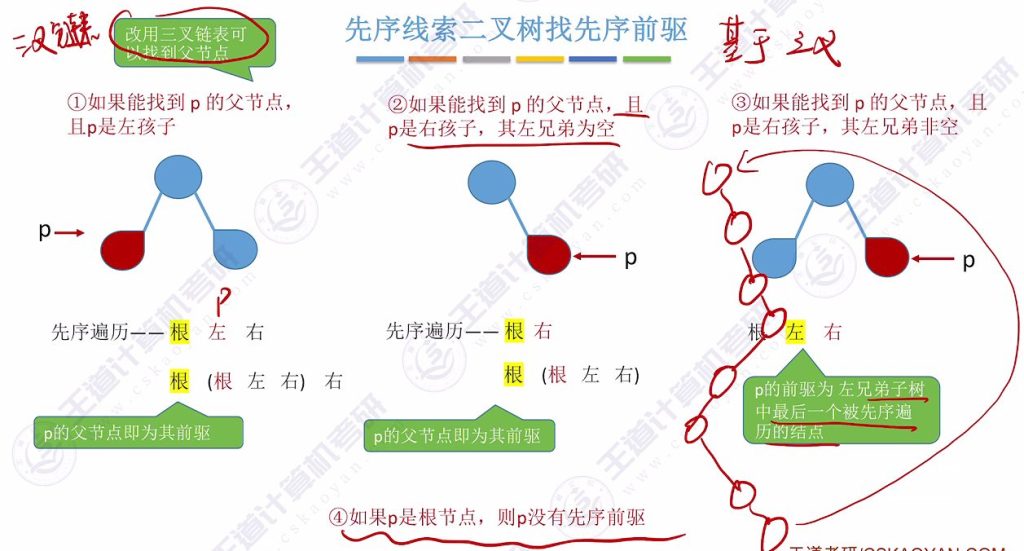
- 三叉链表解决方案:
- p是左孩子:父节点即前驱
- p是右孩子且左兄弟为空:父节点即前驱
- p是右孩子且左兄弟非空:前驱为左兄弟子树最后一个被先序遍历的节点
- p是根节点:无前驱
3.7 后序线索二叉树找后序前继
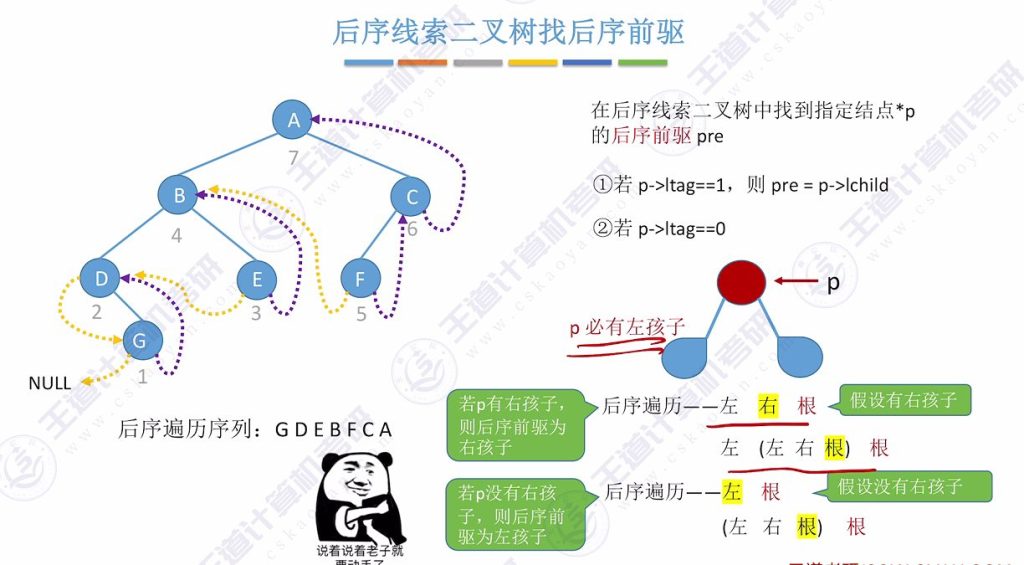
后续前驱
- 有右孩子时:后序前驱为右孩子
- 无右孩子时:后序前驱为左孩子
- 示例:序列ABDGECF中,G的前驱为D,C的前驱为F
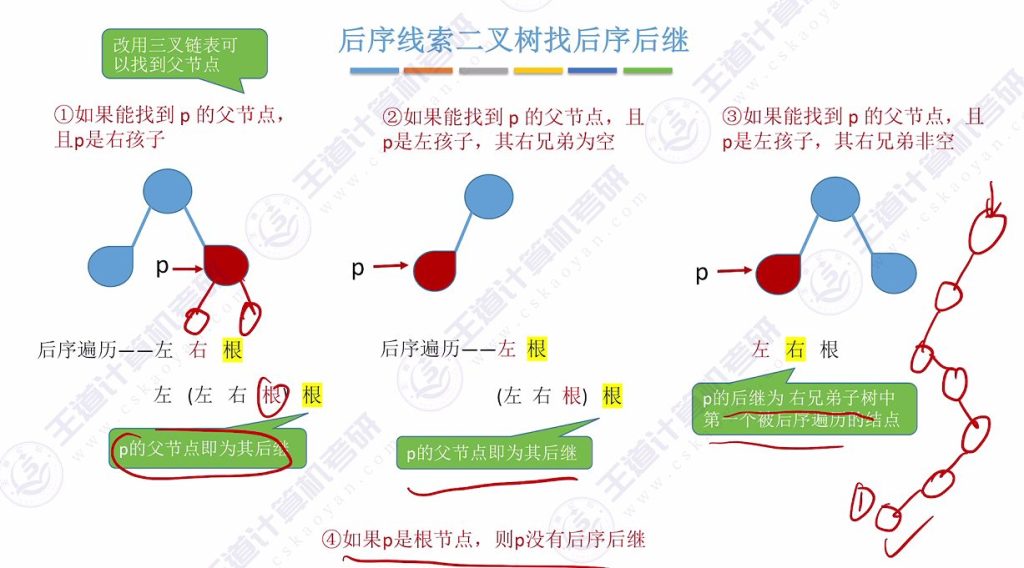
3.8 后序线索二叉树找后序前继
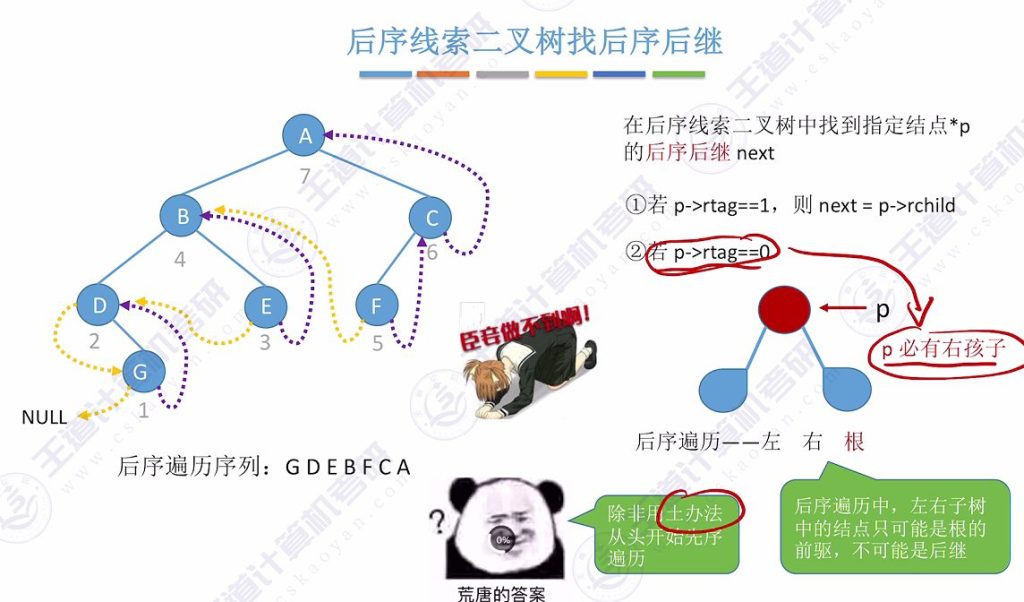
常规限制:无法通过孩子指针找到后继(左右子树只可能是前驱)
- 三叉链表解决方案:
- p是右孩子:父节点即后继
- p是左孩子且右兄弟为空:父节点即后继
- p是左孩子且右兄弟非空:后继为右兄弟子树第一个被后序遍历的节点
- p是根节点:无后继
3.9 知识回顾
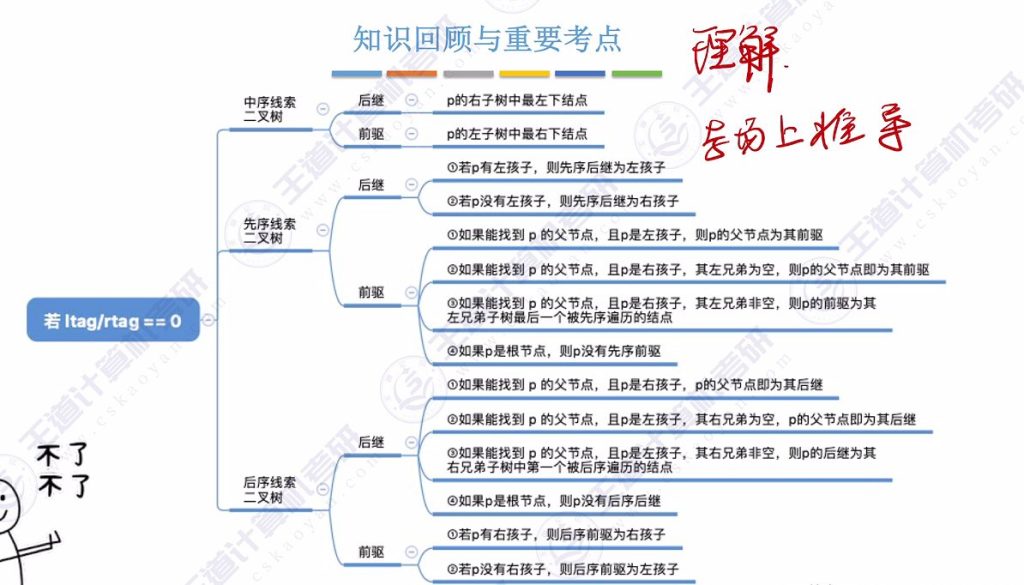
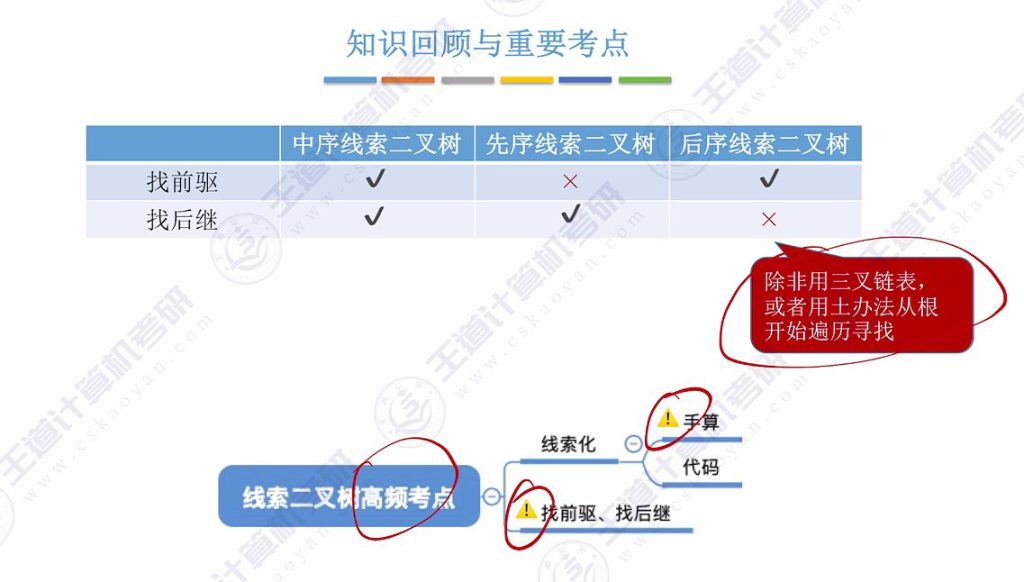
- 中序线索二叉树:
- 可双向遍历(前驱和后继均可找)
- 前驱:左子树最右下节点
- 后继:右子树最左下节点
- 先序线索二叉树:
- 只能正向遍历(仅可找后继)
- 特殊情况:三叉链表可找前驱
- 后序线索二叉树:
- 只能逆向遍历(仅可找前驱)
- 特殊情况:三叉链表可找后继
- 高频考点:
- 手算线索化过程
- 前驱/后继查找算法
- 不同线索二叉树的遍历特性对比
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


