一、树的存储结构
1.1 树的逻辑结构
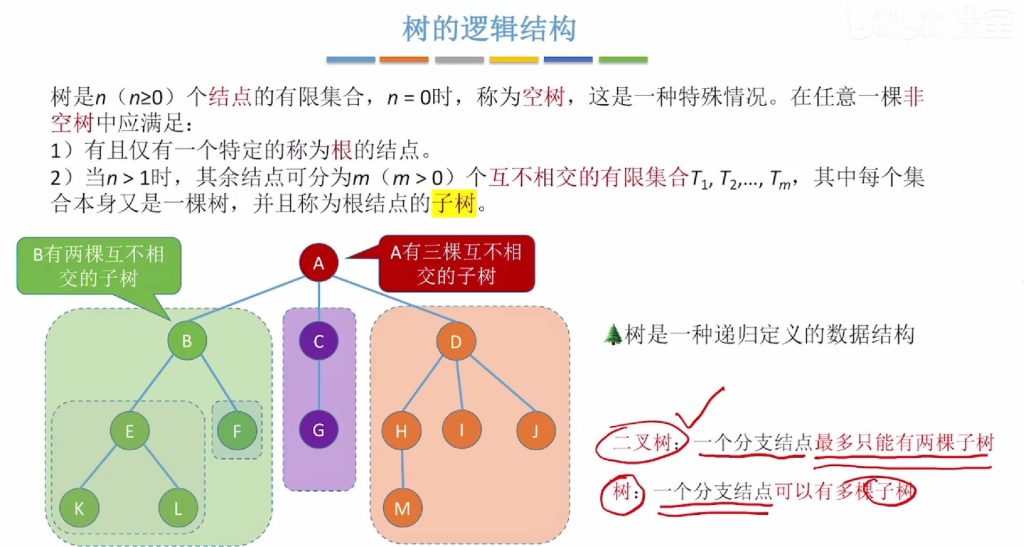
与二叉树的区别: 普通树对分支节点的子树数量无限制,而二叉树最多只能有两棵子树
1.2 二叉树的顺序存储
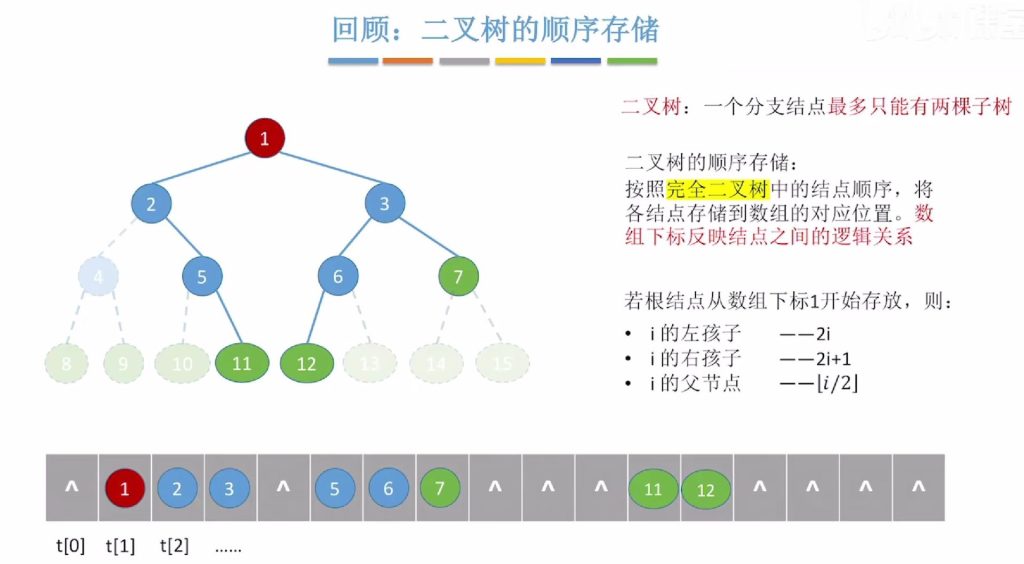
实现方式: 按完全二叉树结点顺序编号并存储在数组中

1.3 如何实现树的顺序结
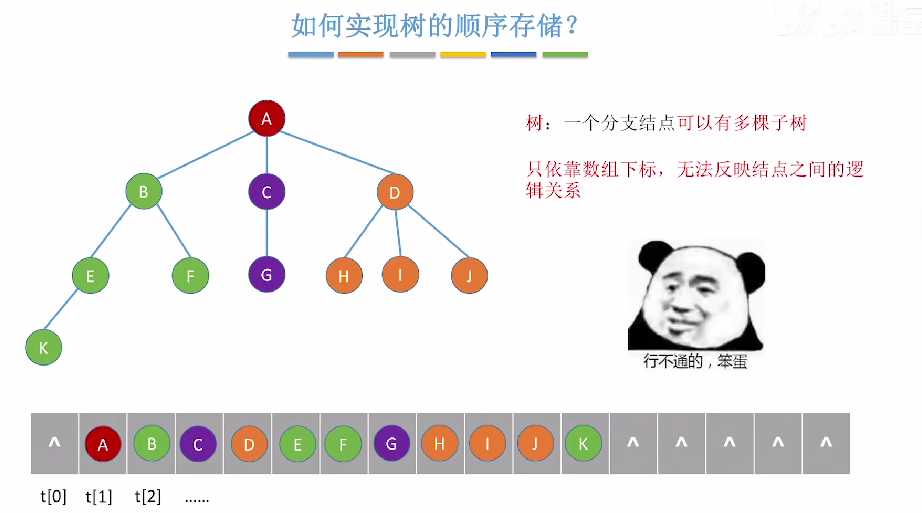
核心问题: 普通树无法像二叉树那样通过数组下标反映逻辑关系
1.4 双亲表示法
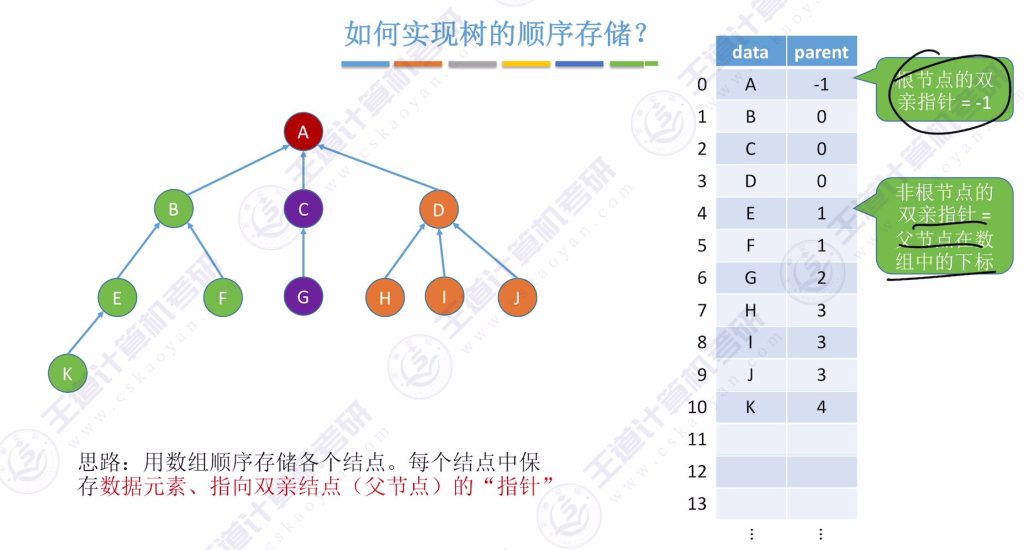
如何实现树的顺序存储?
解决思路: 利用每个非根结点有且仅有一个双亲的特性
树的存储:双亲表示法
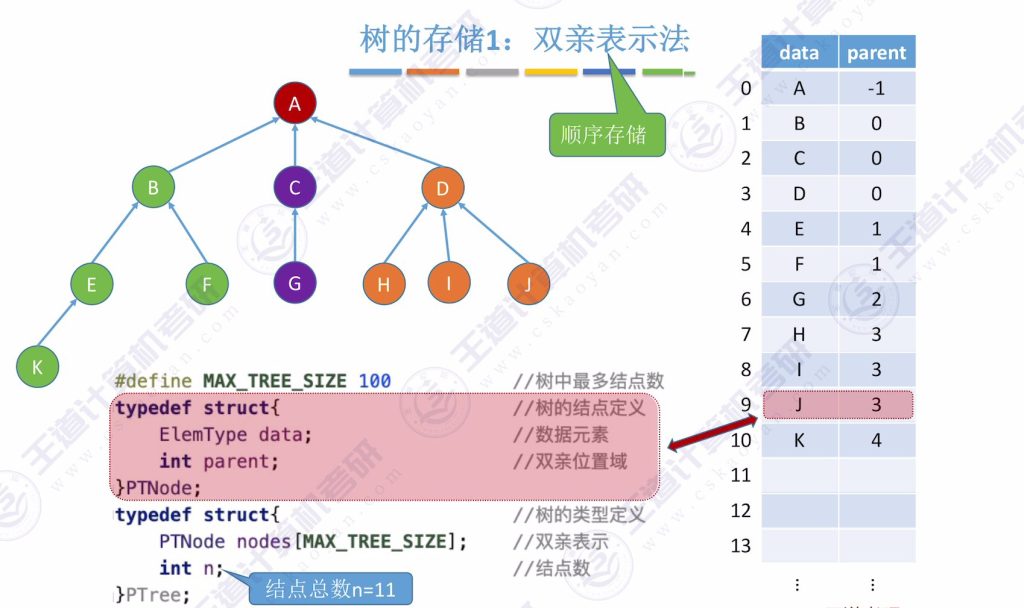
- 存储方式:
- 用数组顺序存储结点
- 每个结点保存数据元素和双亲结点在数组中的下标
- 根结点的双亲指针设为-1
双亲表示法存储“森林”
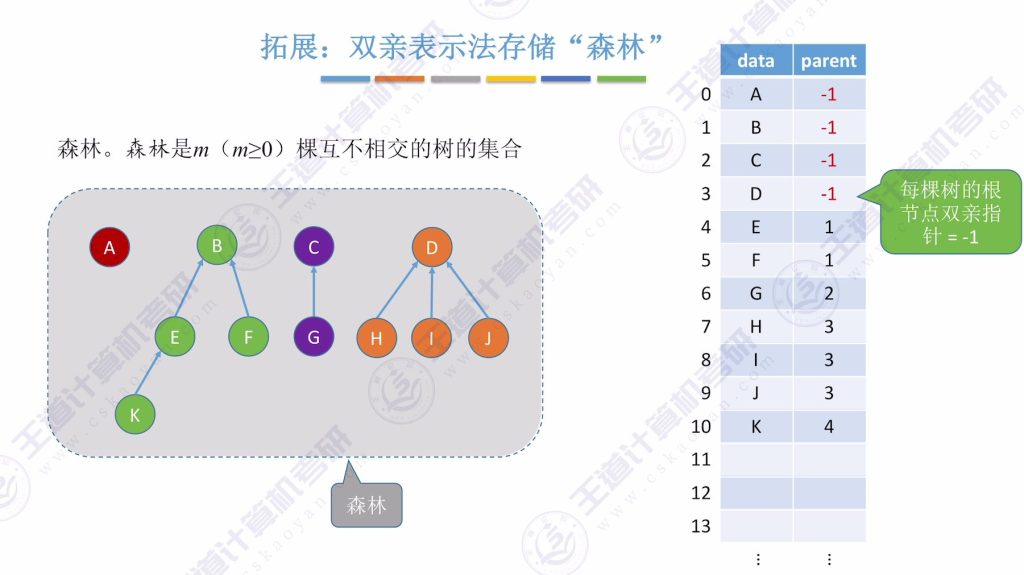
- 森林定义:m(m≥0) 棵互不相交的树的集合
- 存储方式: 将各棵树的根结点的双亲指针都设为-1
双亲表示法的优缺点
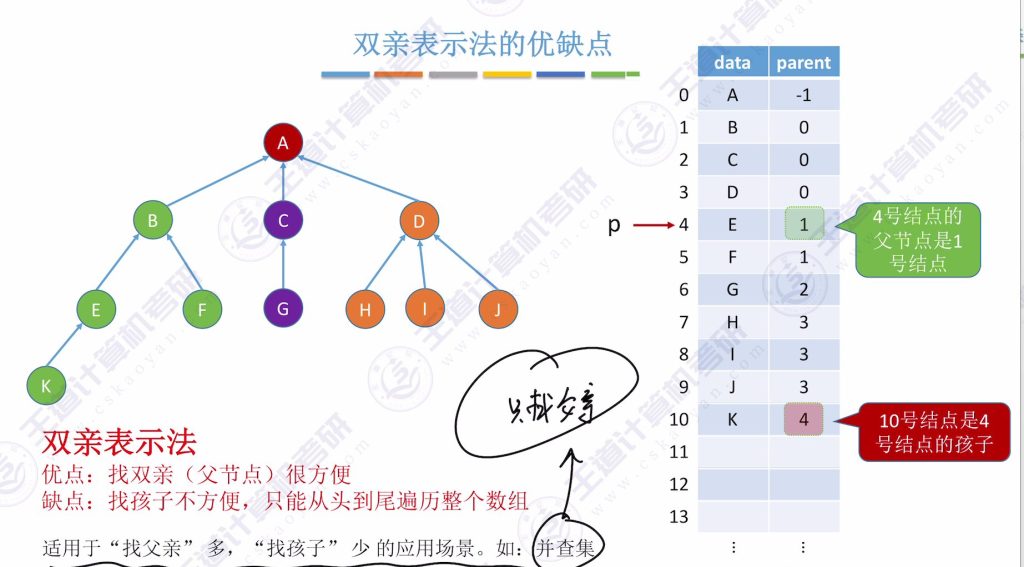
- 优点: 找父节点方便(直接访问parent域)
- 缺点: 找孩子需要遍历整个数组
- 适用场景: “找父亲”多,”找孩子”少的场景(如并查集)
1.5 孩子表示法
树的存储:孩子表示法
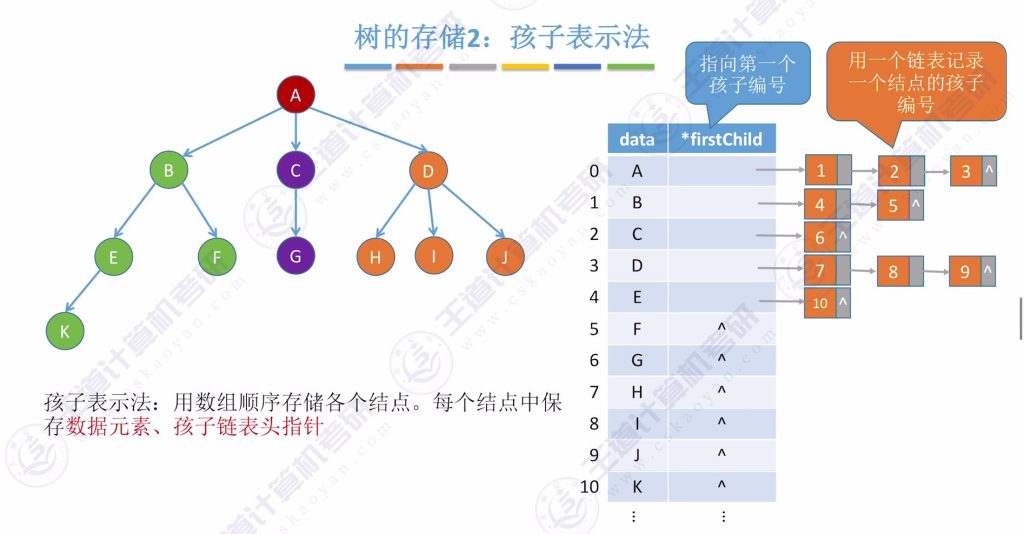
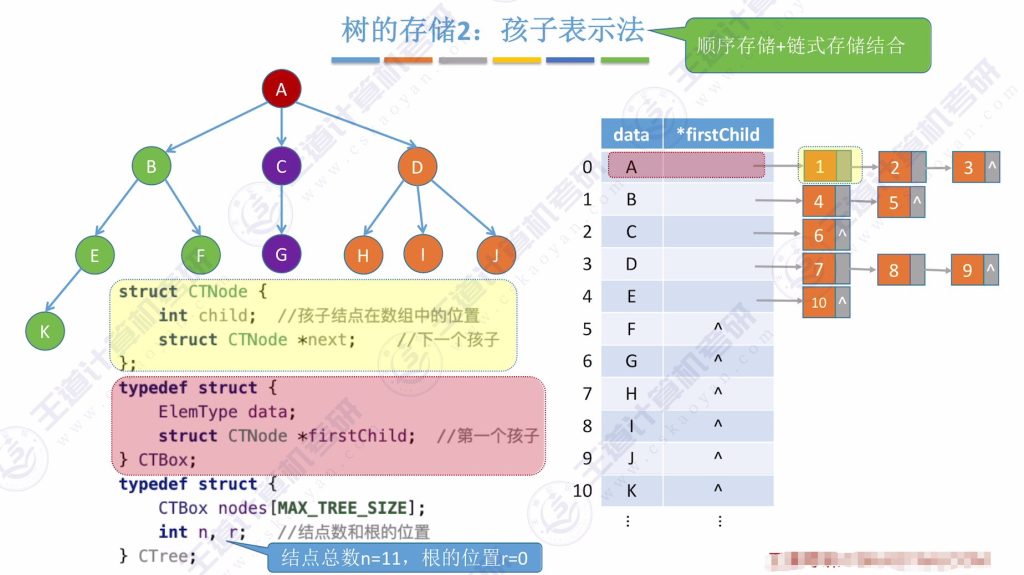
- 存储方式:
- 数组顺序存储结点
- 每个结点保存数据元素和孩子链表头指针
- 链表结点保存孩子在数组中的位置
孩子表示法存储森林
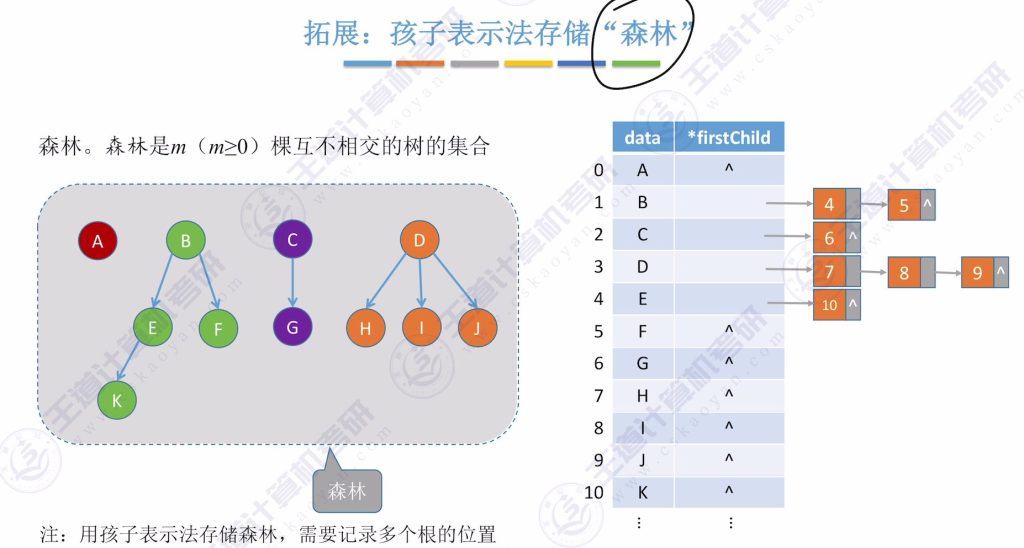
存储方式: 类似树的存储,但需要记录多个根的位置
孩子表示法的优缺点
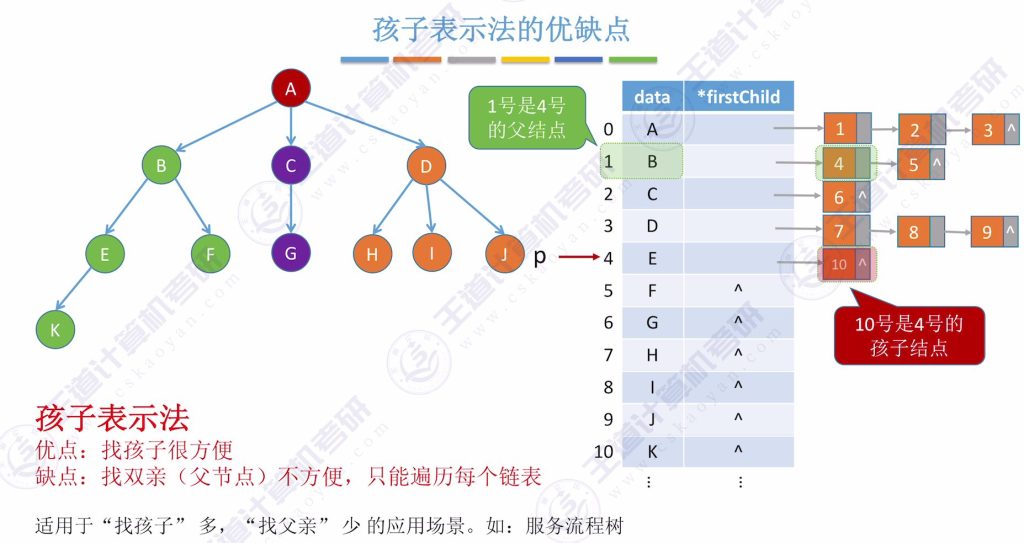
- 优点: 找孩子方便(通过firstChild指针)
- 缺点: 找父节点需要遍历所有链表
- 适用场景: “找孩子”多,”找父亲”少的场景(如服务流程树)
1.6 孩子兄弟表示法
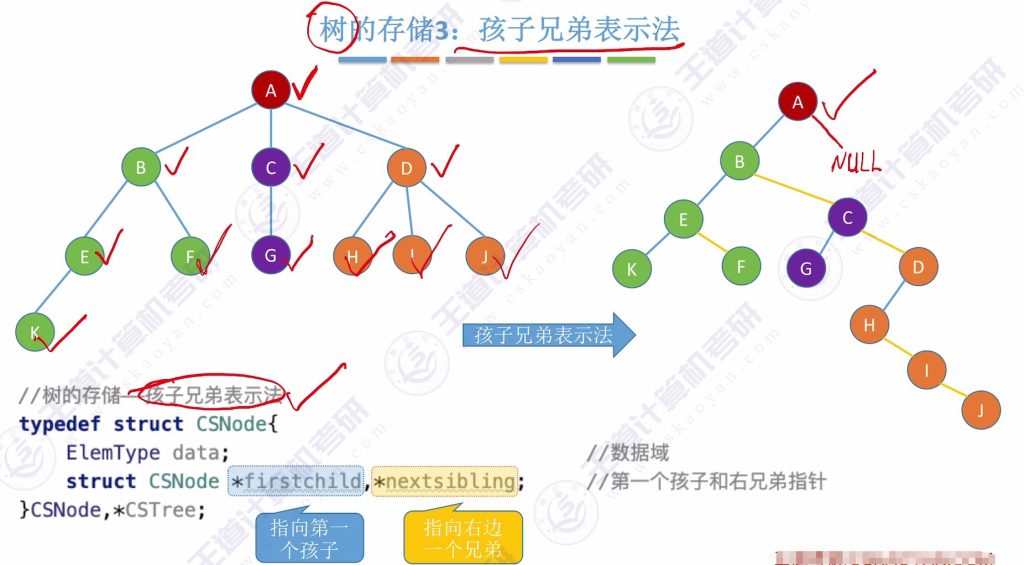
树的孩子兄弟表示法的定义
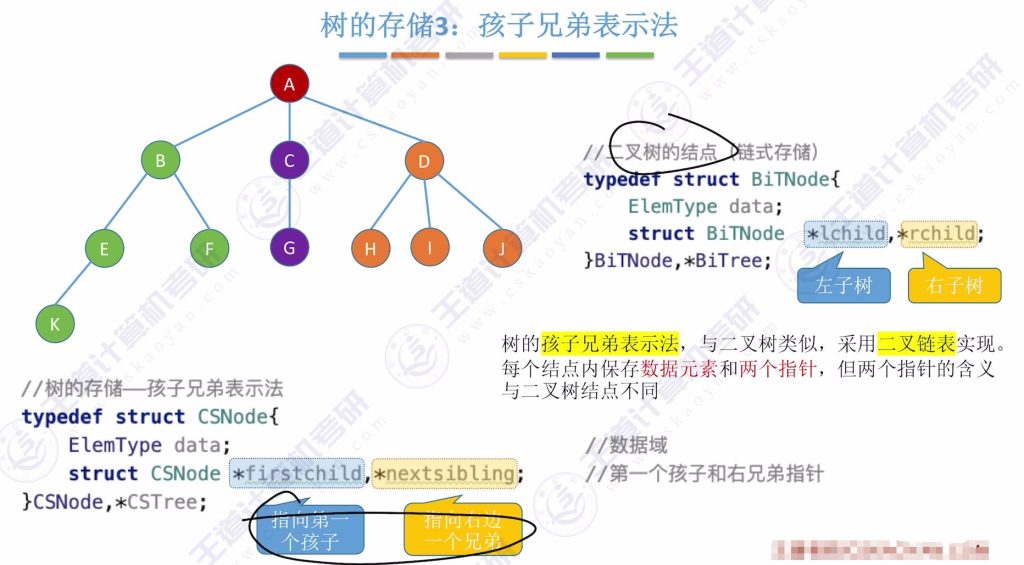
- 存储方式:
- 采用二叉链表
- 结点包含数据域和两个指针:
- firstchild:指向第一个孩子
- nextsibling:指向右边第一个兄弟
孩子兄弟表示法存储森林
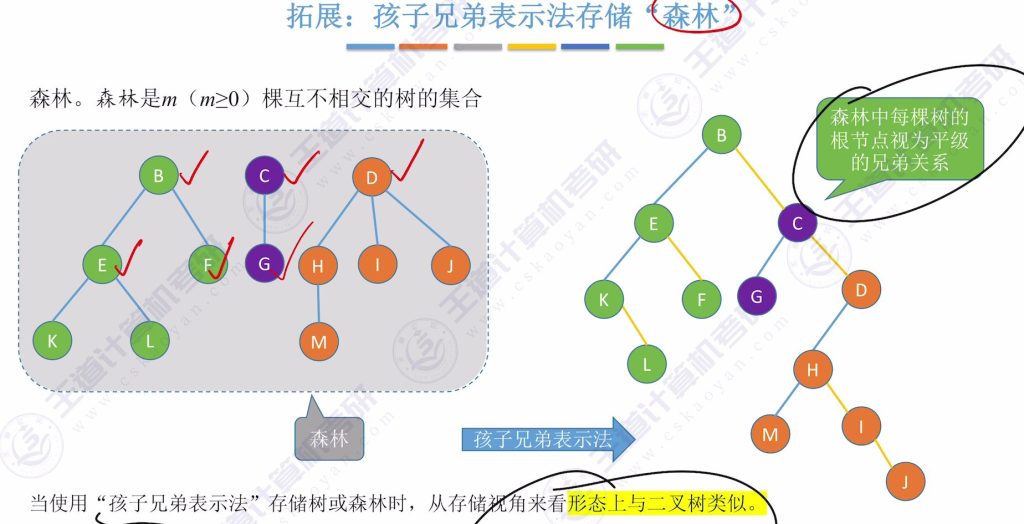
- 存储方式: 将森林中每棵树的根节点视为平级的兄弟关系
- 特点: 存储形态上与二叉树类似,便于树、森林与二叉树之间的转换
1.7 知识回顾
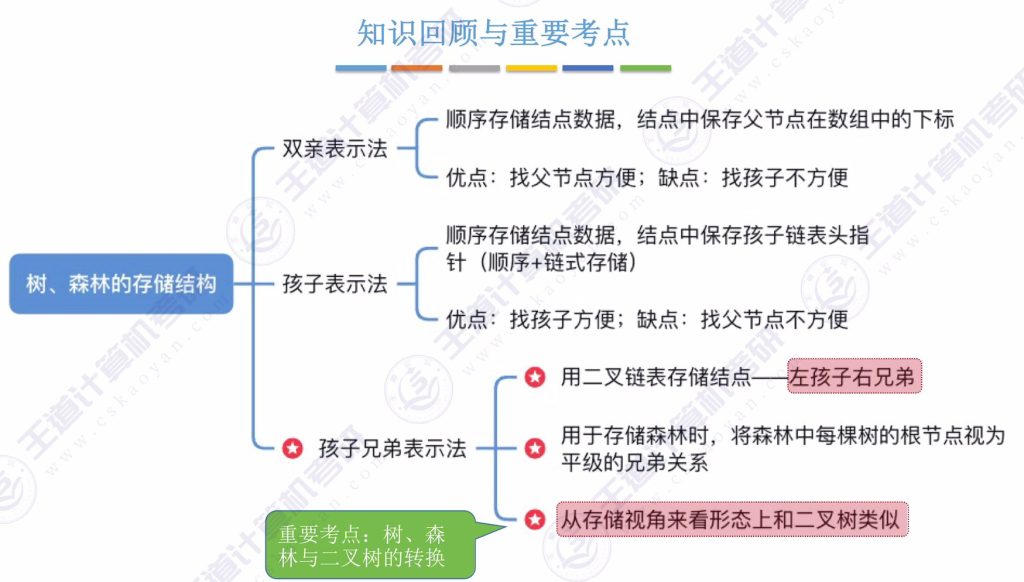
二、树、森林与二叉树的转换(重点)
- 本质:采用孩子兄弟表示法存储树或森林时,其形态与二叉树类似
- 转换类型:包含树转二叉树、森林转二叉树、二叉树转树、二叉树转森林四种转换关系
2.1 树 -> 二叉树的转换
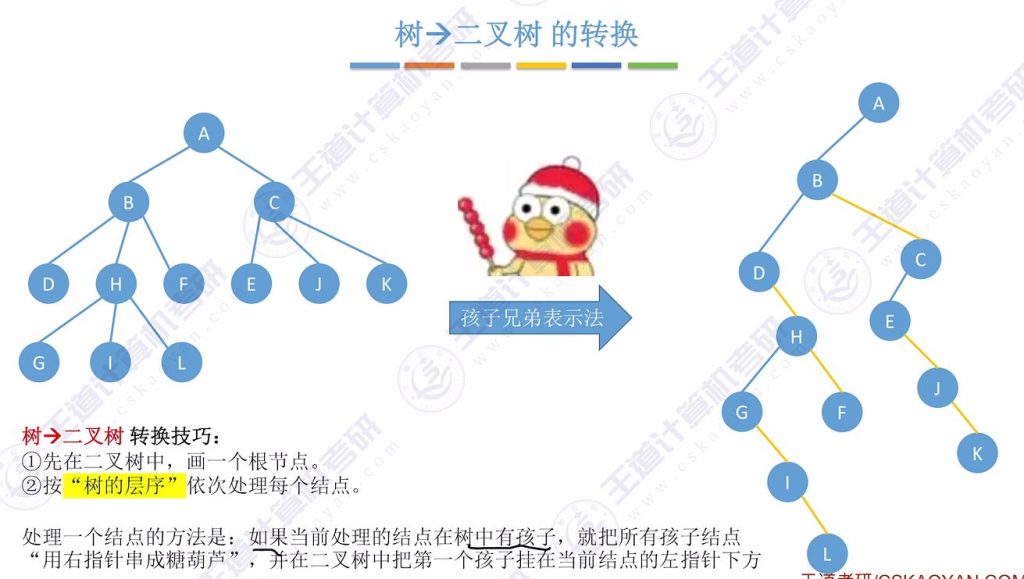
- 转换技巧:
- 在二叉树中画出树的根节点
- 按树的层序依次处理每个节点
- 处理方法:
- 若当前节点有孩子,将所有孩子用右指针串成”糖葫芦”结构
- 将第一个孩子挂在当前节点的左指针下方
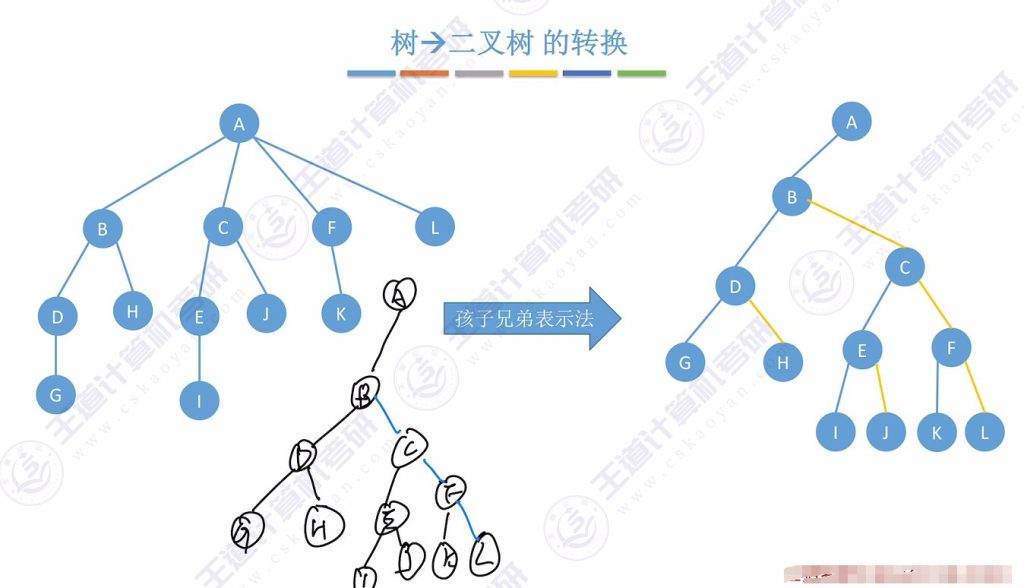
- 示例说明:
- 处理节点A:将孩子B、C用右指针连接,B挂在A的左下方
- 处理节点B:将孩子D、H、F用右指针连接,D挂在B的左下方
- 处理节点C:将孩子E、J、K用右指针连接,E挂在C的左下方
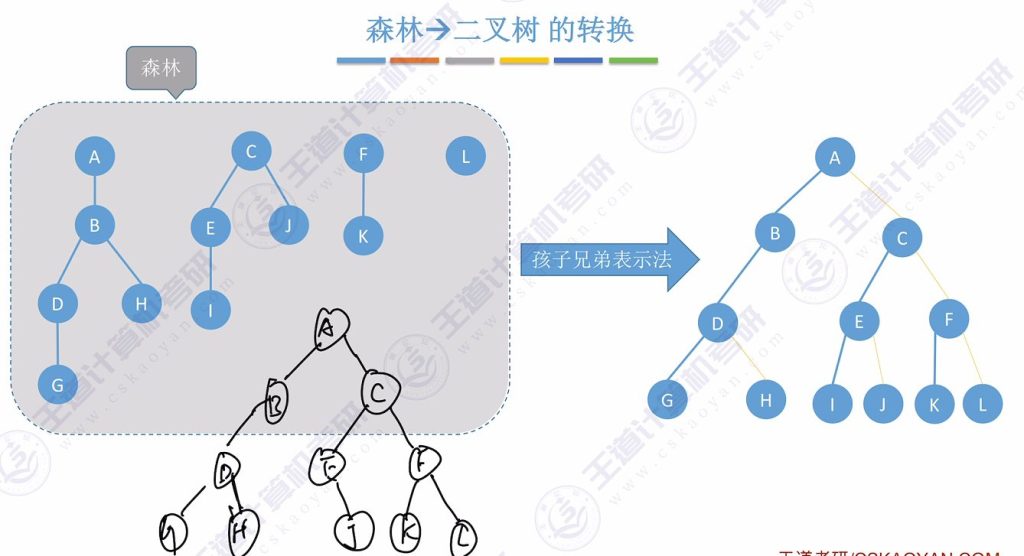
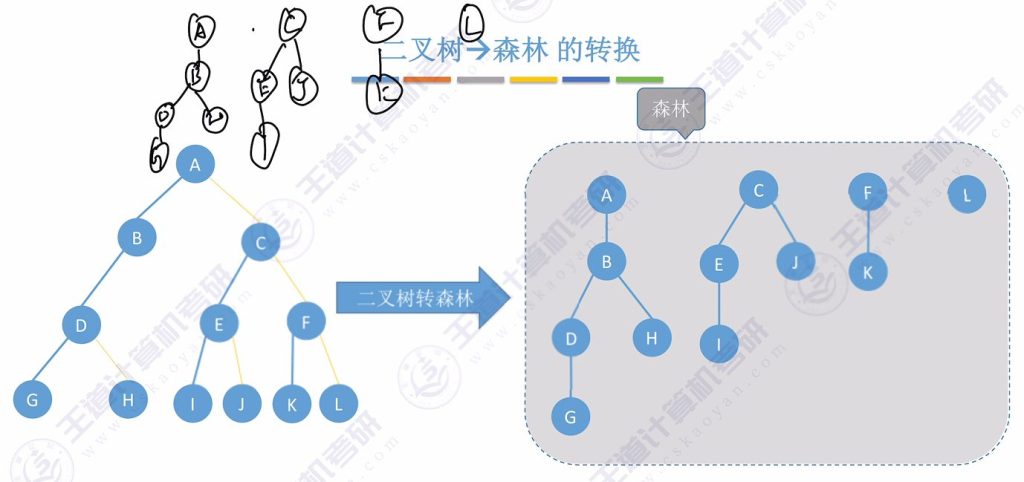
2.2 森林 -> 二叉树的转换
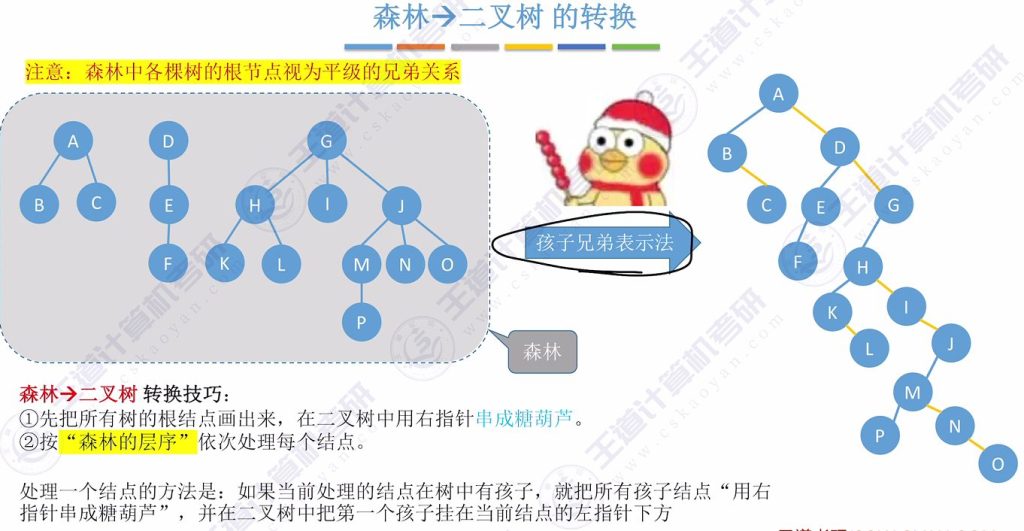
- 关键区别:将森林中各树的根节点视为平级兄弟关系
- 转换步骤:
- 将所有树的根节点用右指针串成”糖葫芦”
- 按森林层序处理每个节点(方法与树转二叉树相同)
- 示例解析:
- 初始连接:根节点A、D、G用右指针串联
- 处理节点A:孩子B、C串联,B挂在A左下方
- 处理节点D:孩子E挂在D左下方
- 处理节点G:孩子H、I、J串联,H挂在G左下方
2.3 二叉树 -> 树的转换
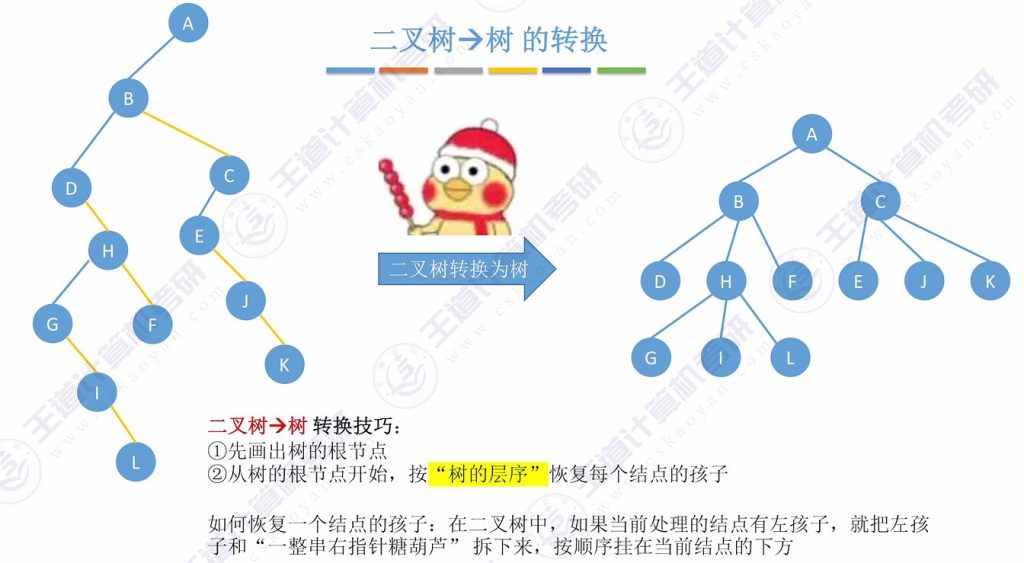
- 转换技巧:
- 画出树的根节点
- 按树层序恢复每个节点的孩子
- 恢复方法:
- 若当前节点有左孩子,将左孩子及其右指针”糖葫芦”整体拆下
- 按顺序挂在当前节点下方作为孩子
- 示例演示:
- 恢复节点A:拆下B、C作为孩子
- 恢复节点B:拆下D、H、F作为孩子
- 恢复节点C:拆下E、J、K作为孩子
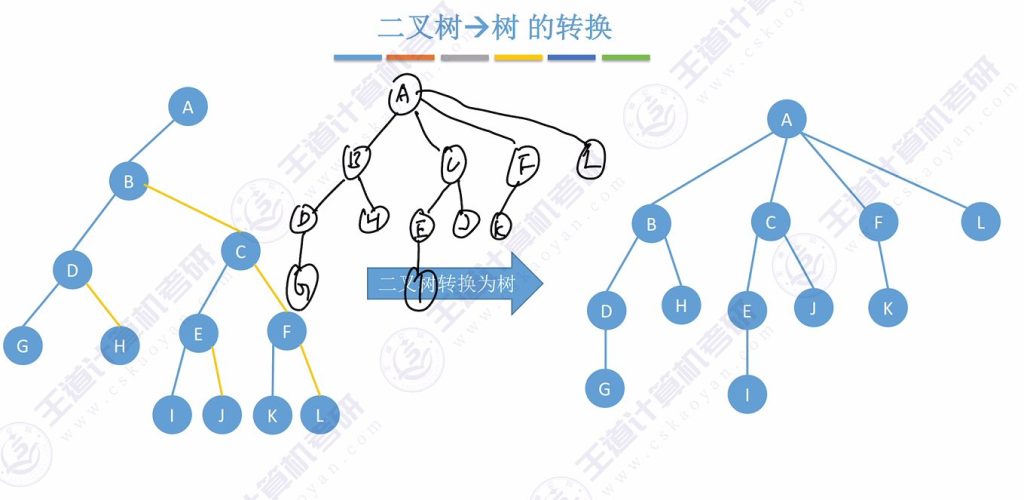
2.4 二叉树 -> 森林的转换
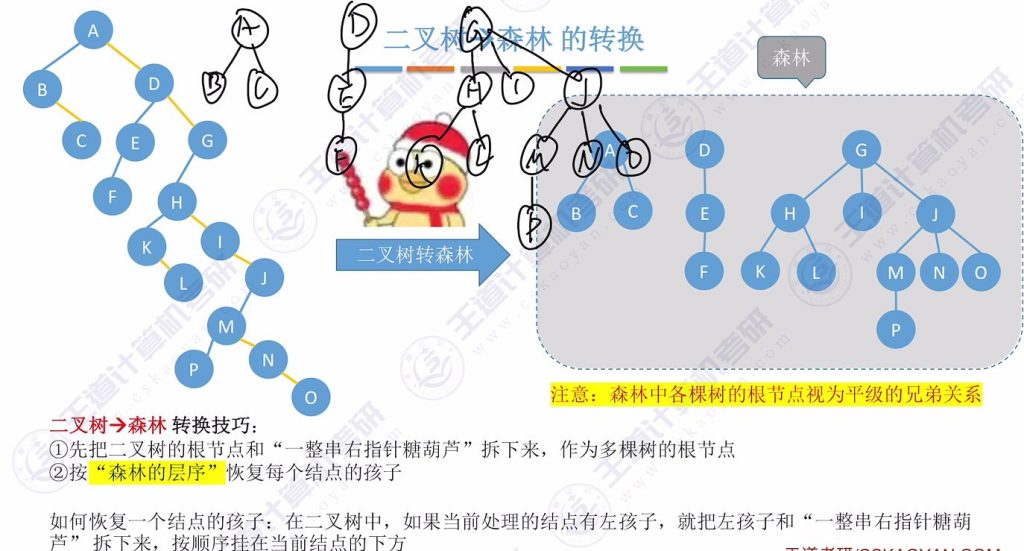
- 关键步骤:
- 将根节点及其右指针”糖葫芦”拆分为多棵树根
- 按森林层序恢复每个节点的孩子(方法与二叉树转树相同)
- 示例分析:
- 初始拆分:A、D、G作为三棵树根
- 恢复节点A:拆下B、C作为孩子
- 恢复节点D:拆下E作为唯一孩子
- 恢复节点G:拆下H、I、J作为孩子
2.5 知识回顾
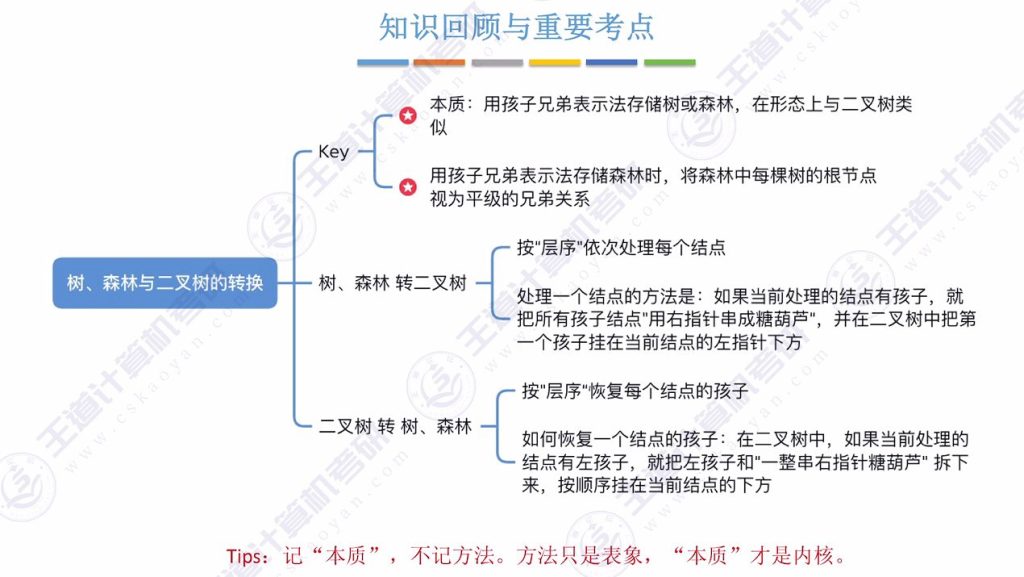
- 核心原理:所有转换本质都是孩子兄弟表示法的应用
- 森林特殊点:必须将各树根视为平级兄弟关系
- 记忆建议:理解存储原理比记忆方法更重要
- 操作规律:
- 转二叉树:孩子变右指针,首孩挂左边
- 转树/森林:左孩加右串变回孩子集合
- 处理顺序:层序处理可避免遗漏和混乱
三、树、森林的遍历
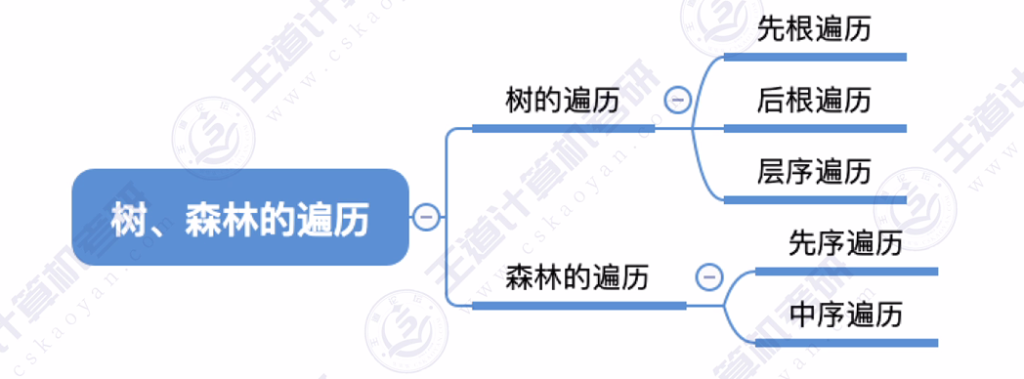
树遍历类型:先根遍历、后根遍历、层序遍历
森林遍历类型:先序遍历、中序遍历
递归特性:树和森林都是递归定义的数据结构,可采用递归算法实现遍历
3.1 树的逻辑结构
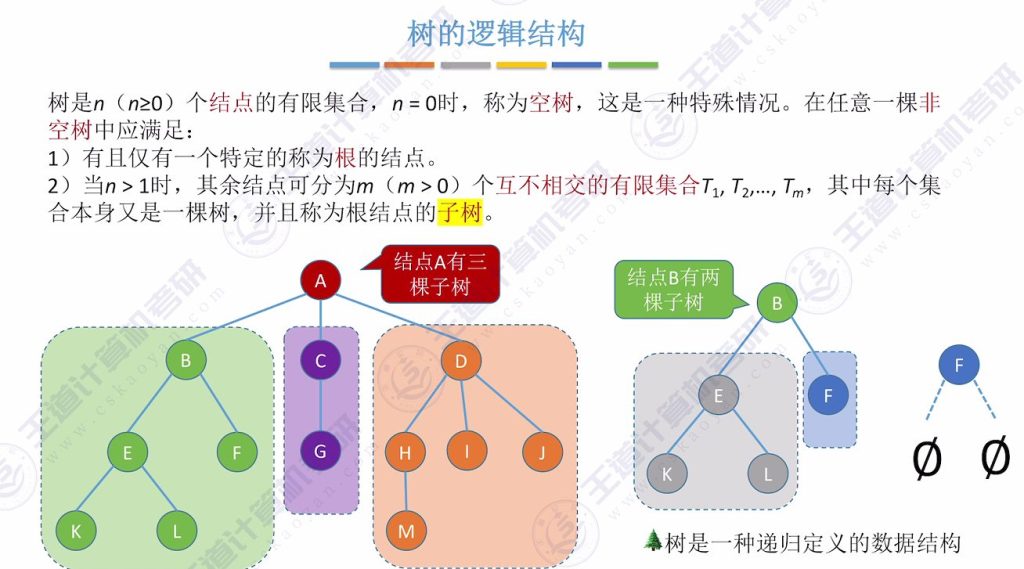
3.2 树的先根遍历
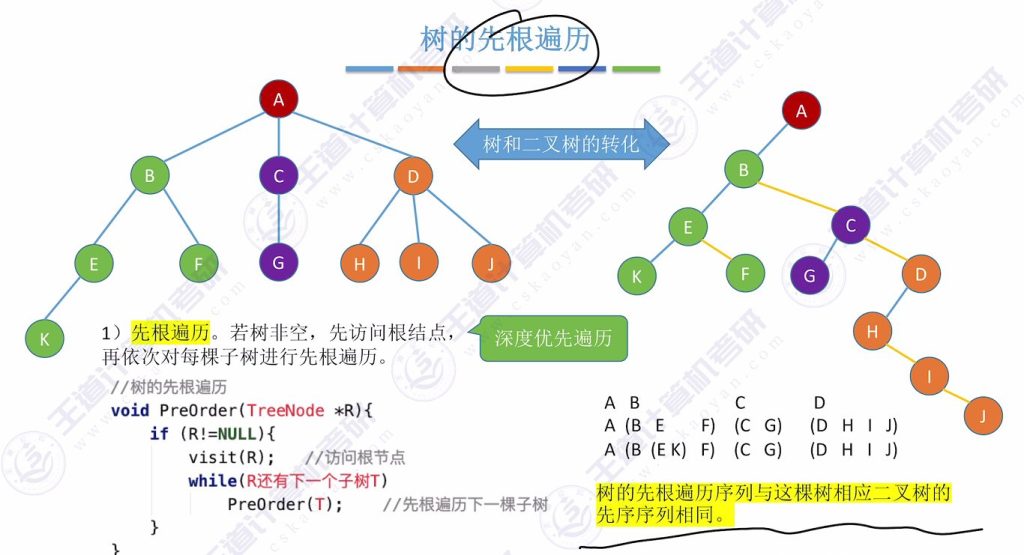
- 定义:若树非空,先访问根结点,再依次对每棵子树进行先根遍历
- 算法实现:
- 访问顺序:根节点→左子树→右子树(与二叉树先序遍历类似)
- 示例:对图示树先根遍历序列为A→B→E→K→F→C→G→D→H→I→J
- 与二叉树关系:树的先根遍历序列与其对应二叉树(孩子兄弟表示法)的先序序列相同
3.3 树的后根遍历
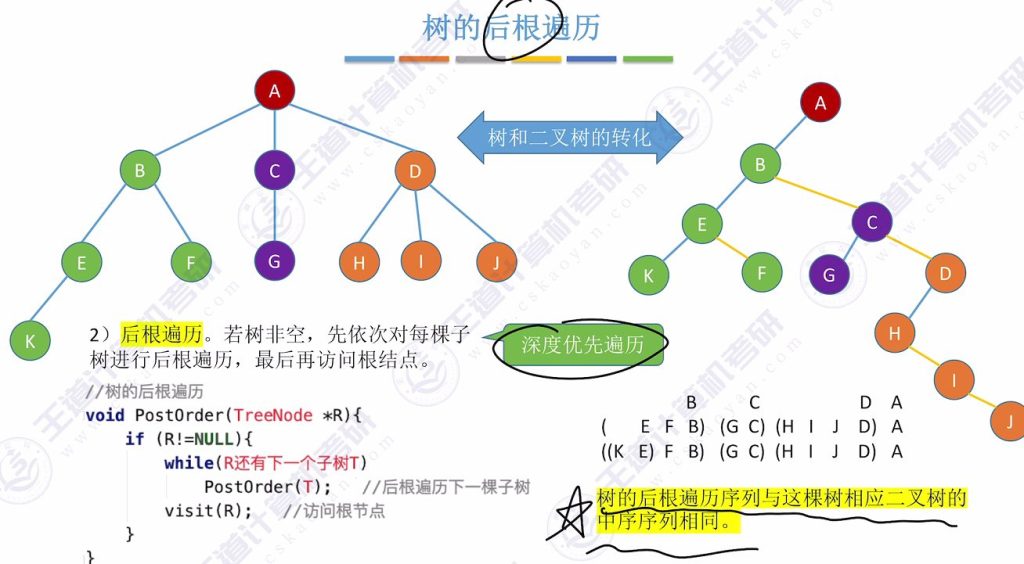
- 定义:若树非空,先依次对每棵子树进行后根遍历,最后访问根结点
- 算法实现:
- 访问顺序:子树遍历完成后再访问根节点
- 示例:图示树后根遍历序列为K→F→E→B→G→C→H→I→J→D→A
- 与二叉树关系:树的后根遍历序列与其对应二叉树的中序序列相同
- 遍历特性:属于深度优先遍历(优先往深处探索)
3.4 树的层次遍历
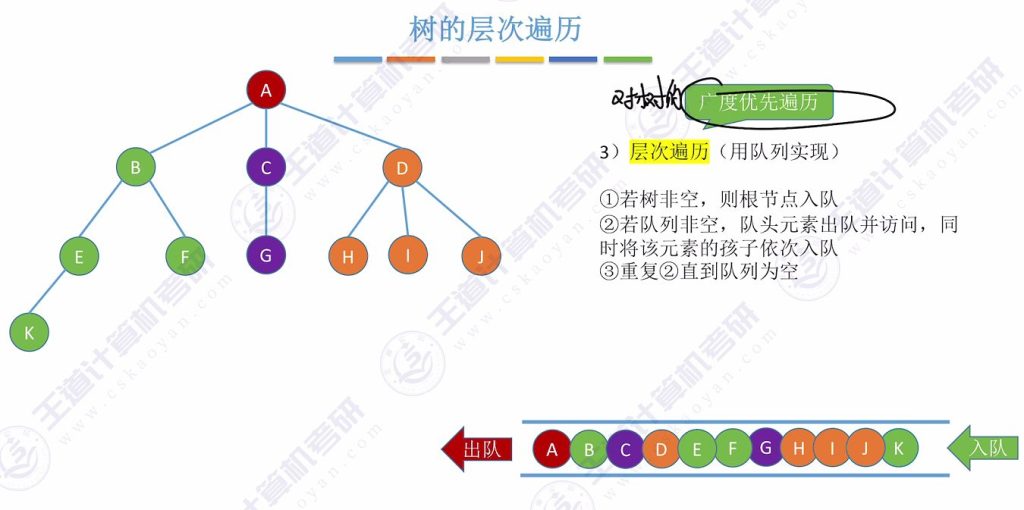
- 实现方法:使用辅助队列
- 根节点入队
- 队头元素出队并访问
- 将该元素的孩子依次入队
- 重复2-3直到队列为空
- 示例:图示树层次遍历序列为A→B→C→D→E→F→G→H→I→J→K
- 遍历特性:属于广度优先遍历(优先横向探索)
- 与深度优先对比:先根/后根遍历是深度优先,层次遍历是广度优先
3.5 森林的先序遍历
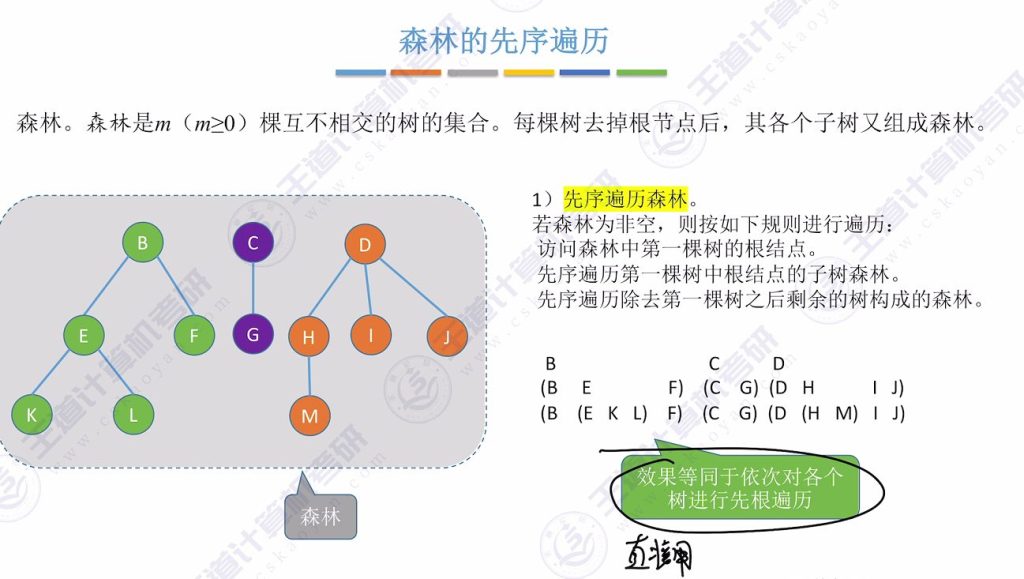
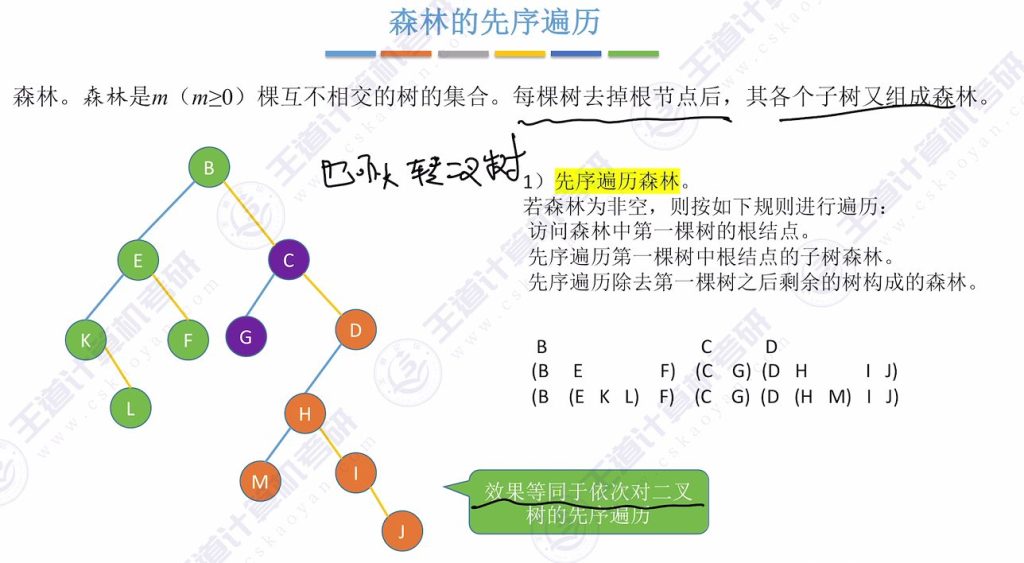
- 定义:森林由 m (m≥0)棵互不相交的树组成
- 遍历规则:
- 访问第一棵树的根结点
- 先序遍历第一棵树的子树森林
- 先序遍历剩余树构成的森林
- 等效方法:
- 依次对各树进行先根遍历
- 转换为二叉树执行先序遍历
- 递归特性:包含两层递归嵌套(森林递归+树递归)
3.6 森林的中序遍历
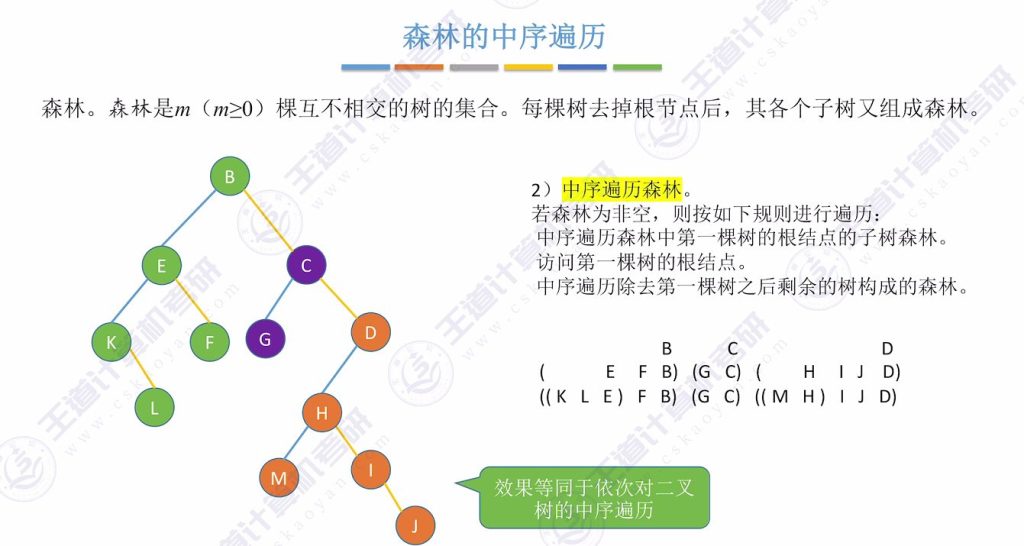
- 遍历规则:
- 中序遍历第一棵树的子树森林
- 访问第一棵树的根结点
- 中序遍历剩余树构成的森林
- 等效方法:
- 依次对各树进行后根遍历
- 转换为二叉树后执行中序遍历
- 实现技巧:建议用孩子兄弟表示法存储森林,转换为二叉树遍历问题
3.7 重要知识点回顾

- 对应关系:
- 树先根遍历 ≡ 二叉树先序遍历
- 树后根遍历 ≡ 二叉树中序遍历
- 森林先序遍历 ≡ 二叉树先序遍历
- 森林中序遍历 ≡ 二叉树中序遍历
- 解题技巧:
- 优先选择熟悉的解题角度(直接遍历或转换为二叉树)
- 森林遍历可分解为对各树的单独遍历
- 注意递归定义的特性在算法实现中的应用
树和森林遍历操作关键知识点:
1、树的遍历包括三种方式:先根遍历(先访问根节点,然后依次对各个子树执行先根遍历)、后根遍历(先对各个子树进行后根遍历,然后访问根节点)、层序遍历(使用辅助队列实现,根节点入队后队头元素出队并访问,该元素的所有孩子节点依次入队,重复此过程直到队列为空)。
2、深度优先遍历包括先根遍历和后根遍历,特点是尽可能往深处探索到达尽头后才返回。广度优先遍历即层序遍历,特点是尽可能横向探索。
3、森林的遍历包括先序遍历和中序遍历。先序遍历是访问森林中第一棵树的根节点,然后先序遍历第一棵树的子树森林,最后先序遍历除第一棵树外的剩余树组成的森林。中序遍历定义较复杂有两层递归嵌套。
4、简化方法:森林先序遍历等同于依次对各个子树执行先根遍历,森林中序遍历等同于依次对各个子树执行后根遍历。
5、重要的等价关系:树的先根遍历等价于二叉树先序遍历,树的后根遍历等价于二叉树中序遍历,森林先序遍历等价于二叉树先序遍历,森林中序遍历等价于二叉树中序遍历。
6、解题策略有三种:直接遍历法(按定义递归遍历)、转换法(将树或森林转换为二叉树后对二叉树进行相应遍历操作)、编程实现(使用孩子兄弟表示法存储森林并将森林遍历转换为二叉树遍历)。
7、关键提示:理解递归特性,掌握等价关系,选择合适方法,避免复杂递归,实际编程推荐使用孩子兄弟表示法转换为二叉树操作
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


