第五章 06并查集（王道）

一、知识总览

二、如何表示集合关系

2.1 逻辑结构—集合

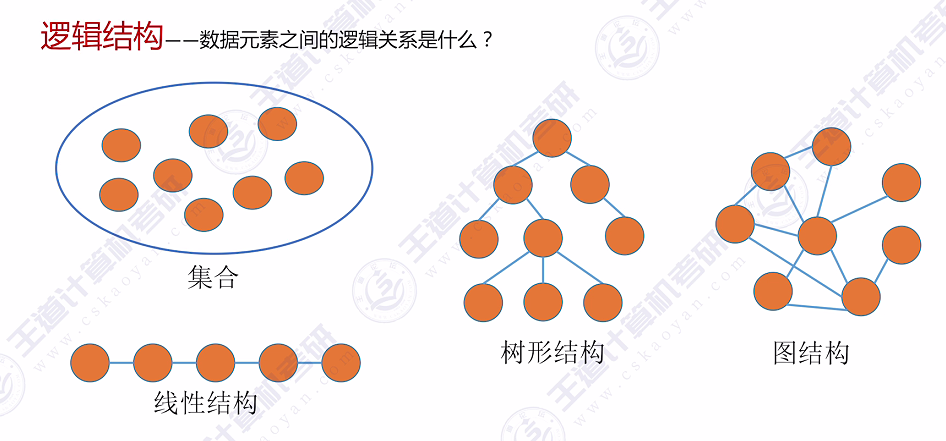
本质特征: 并查集本质上是表示集合类型的逻辑结构，数据元素之间呈现集合关系

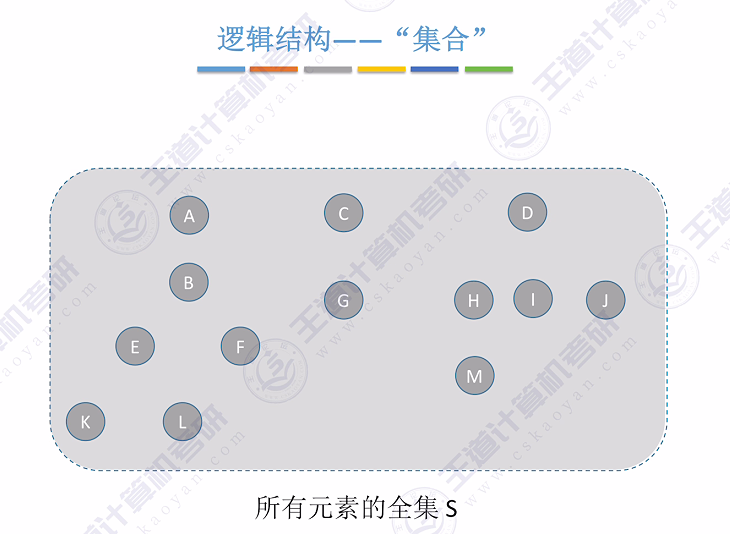
数学概念: 集合在数学中很常用，如一个班所有同学构成集合S，元素a,b,c,d等代表各个同学

2.2 如何表示集合的逻辑关系？

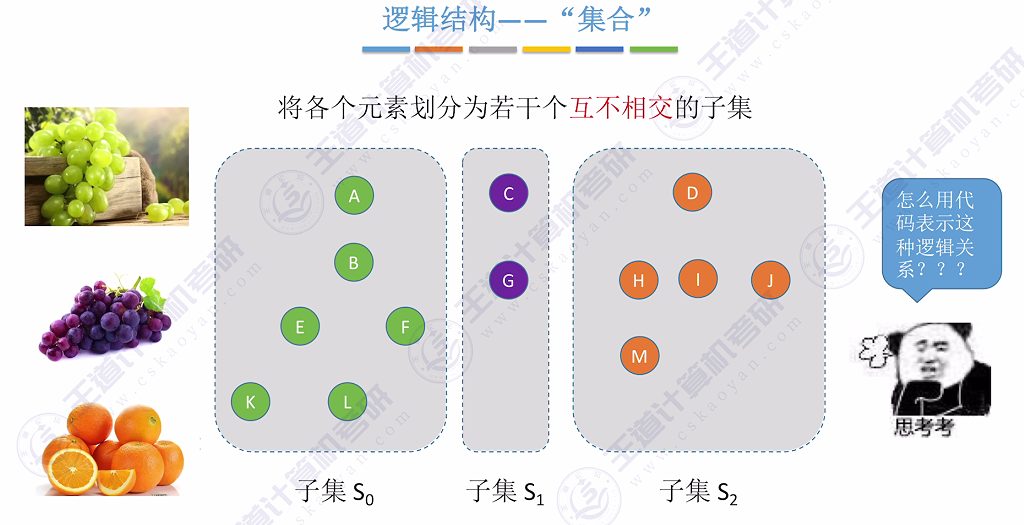
子集划分: 可按不同维度将全集划分为若干互不相交的子集，如按水果喜好分类

元素关系: 任意两元素间只存在两种关系——同属一个集合或分属不同集合

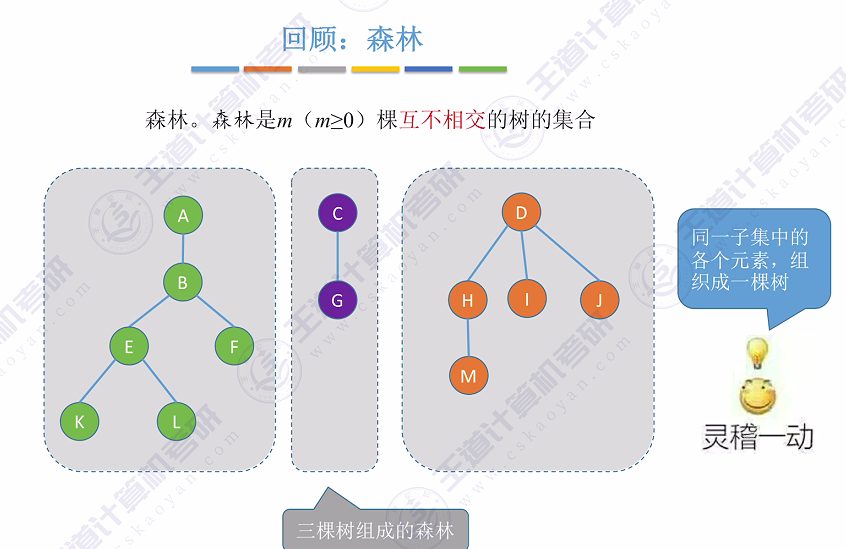
• 森林定义: 森林是m(m≥0)棵互不相交的树的集合
• 结构类比: 森林中互不相交的树与集合中互不相交的子集具有相似性

2.3 用互不相交的树表示多个集合

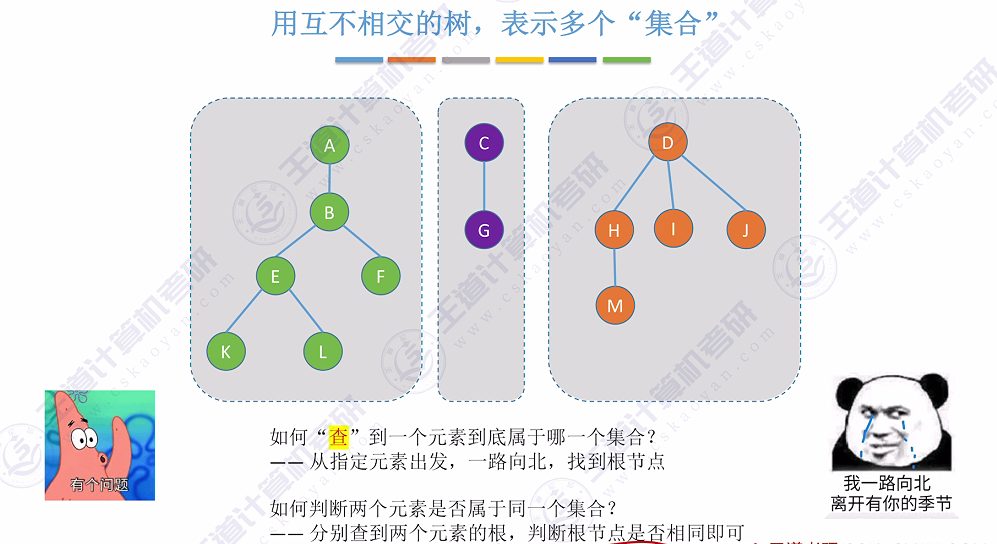
• 存储思路: 将同一子集的元素组织成一棵树，不同子集对应不同树
• 实现原理: 通过树形结构表示元素归属关系，树根代表集合标识符

2.4 回顾：树的双亲表示法

• 优势分析:
  • 查操作高效：指针向上指，便于查找根节点
  • 并操作简单：只需修改根节点的父指针
• 实现原理: parent=4表示父节点的数组下标为4

2.5 并查集的存储结构

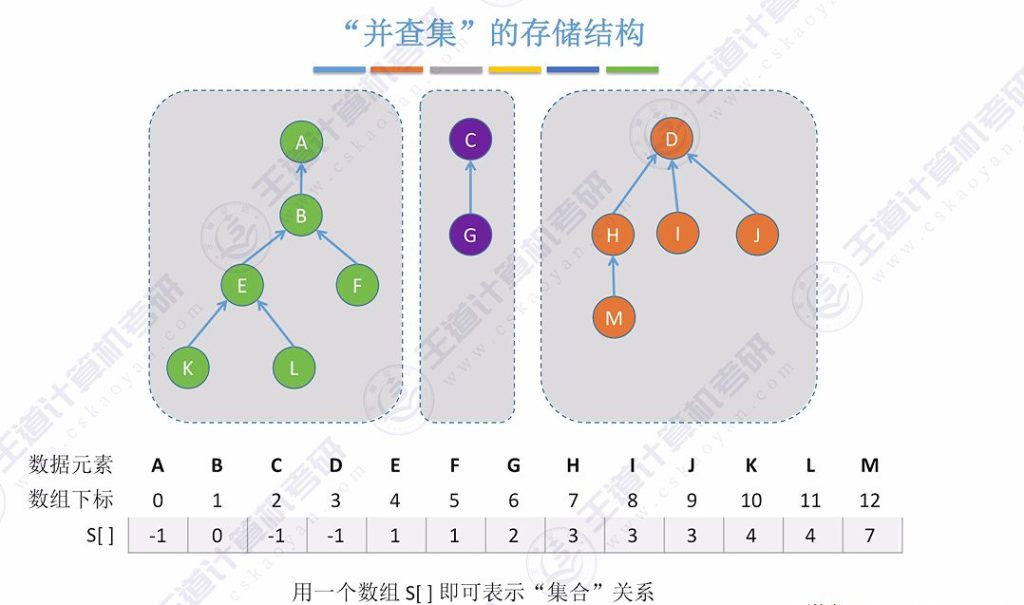
• 核心结构: 使用长度为n的int型数组 S[ ] 表示集合关系
• 存储原理: 采用双亲表示法，数组元素值表示父节点的数组下标
• 根节点标识: 根节点的数组值为-1
• 示例解析: 如元素l(下标11)的父节点是e(下标4)，故S[11]=4；A为根节点故S[0]=−1.

2.6 并查集的基本操作

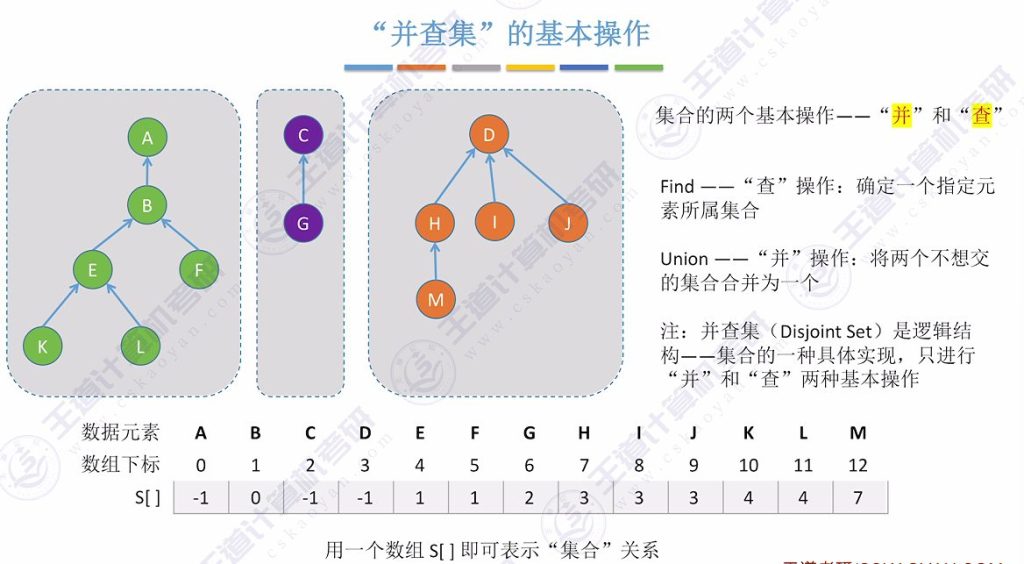
• 逻辑结构：并查集(Disjoint Set)是集合逻辑结构的具体实现，专门处理不相交集合的合并与查询问题
• 核心操作：
  • Find操作：确定指定元素所属的集合（通过查找根节点实现）
  • Union操作：将两个不相交集合合并为一个集合
• 存储方式：使用数组S[]表示集合关系，数组下标对应元素编号，数组值表示父节点索引（负值表示根节点）

查操作

• 操作定义: 查找指定元素所属的集合
• 实现方法: 从该元素出发”一路向北”查找根节点，根节点即代表集合标识
• 判断原理: 不同树的根节点不同，相同树的根节点相同

并操作

• 操作定义: 将两个集合合并为一个集合
• 实现方法: 使一棵树成为另一棵树的子树，如将c连到a的根节点下
• 名称由来: “并查集”名称即来源于需要实现”并”和”查”两个基本操作

三、并查集的代码实现

3.1 并、查的代码实现

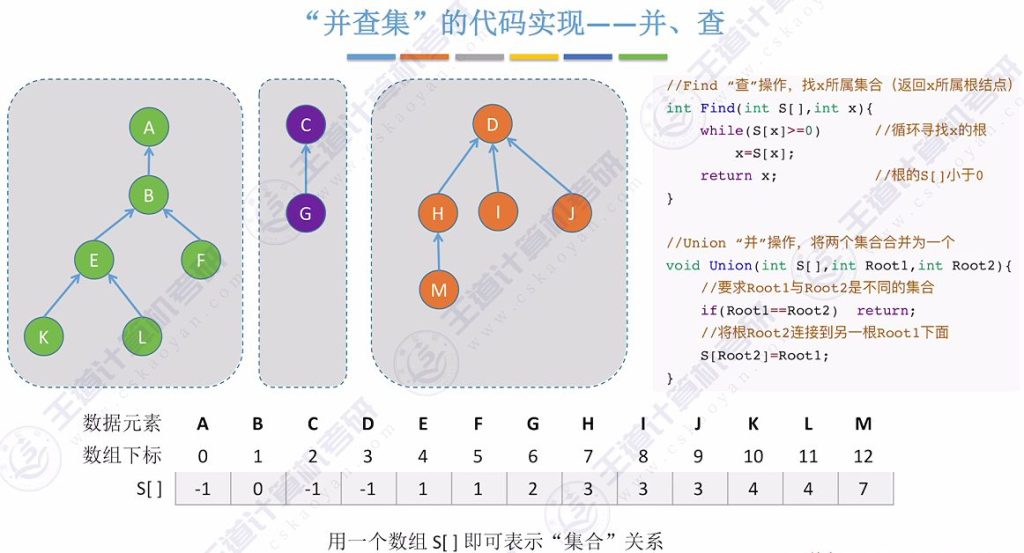
初始化并查集

• 实现原理：将每个元素初始化为独立的子集，数组元素值设为−1
• 代码示例：
• 初始状态：所有元素自成集合，如元素A(0)、B(1)…L(11)对应的S[]值均为−1

查操作实现

• 算法流程：从指定元素开始，沿父指针向上查找直到根节点（S[x]<0的节点）
• 实例演示：查找元素L(11)的归属路径为11→4→1→0，最终返回根节点A(0)
• 时间复杂度：与树的高度成正比，最坏情况O(n)

并操作实现

• 合并条件：必须确保两个集合的根节点不同（避免重复合并）
• 实现方法：将一个集合的根节点指向另一个集合的根节点
• 操作示例：合并根节点为A(0)和C(2)的集合时，执行S[2]=0
• 合并策略：常规合并可能导致树高度增加，后续可优化（按秩合并）
• 复合操作：合并两个非根元素时，需先执行Find确定根节点再Union

3.2 并、查时间复杂度分析

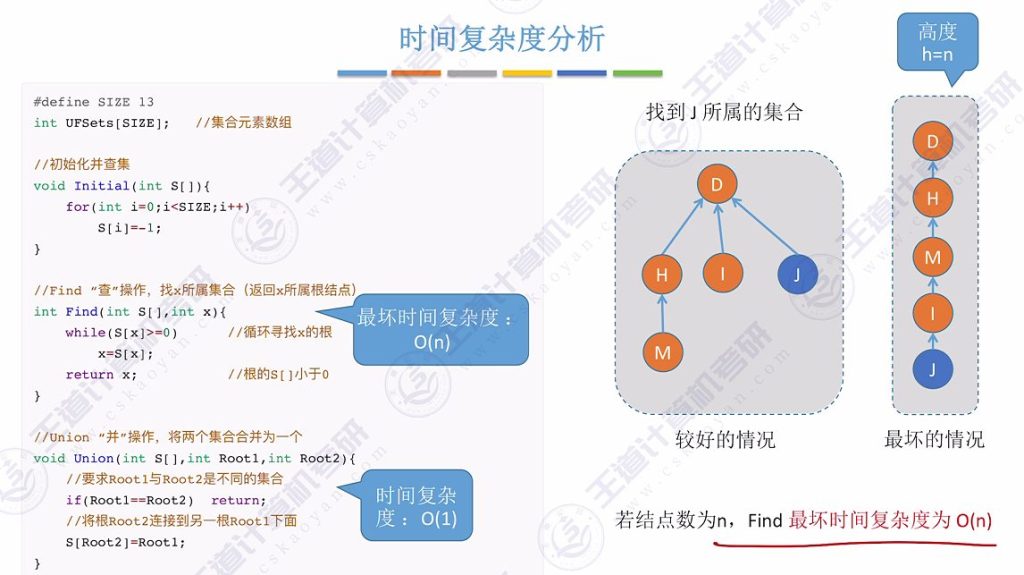
1）基本操作时间复杂度

• Union操作复杂度: 仅需给出两个集合的根节点，时间复杂度为常数级O(1)
• Find操作复杂度: 最坏情况下需要O(n)时间复杂度

2）时间复杂度影响因素

• 关键因素: Find操作的时间复杂度直接与树的高度h相关
• 优化思路: 通过控制树的高度来降低时间复杂度，使树结构尽量扁平而非瘦高
• 极端情况示例:
  • 理想情况：只需向上查找一次即可找到根节点
  • 最坏情况：需要从叶子节点逐层向上遍历整棵树

3）优化方向

• 核心目标: 降低Find操作的时间复杂度
• 实现方法: 在构造树结构时控制其高度增长
  • 避免形成线性链式结构
  • 采用平衡策略使树结构更加扁平化
• 预期效果: 将最坏时间复杂度从O(n)降低到更优级别

四、Union 操作的优化

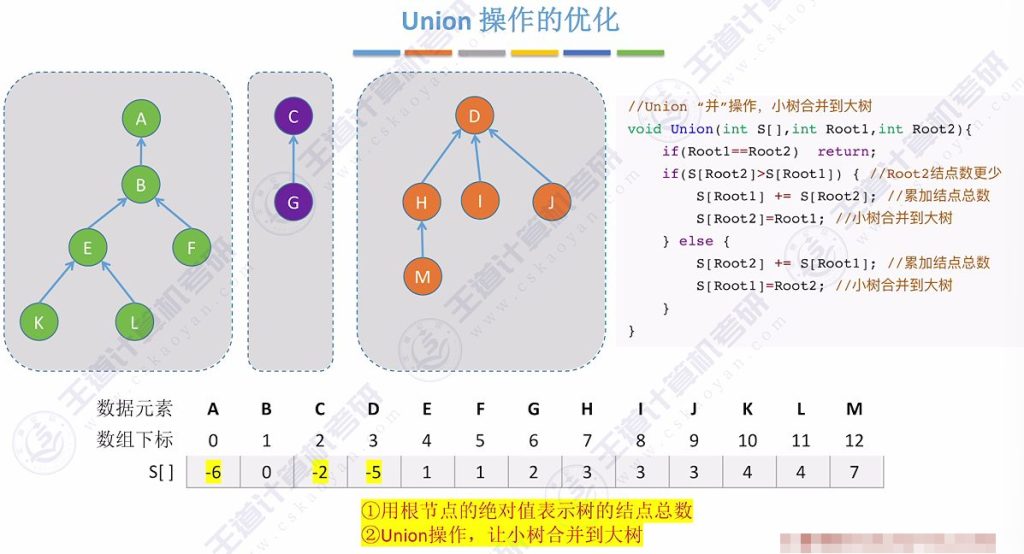
4.1 Union 操作的优化

优化思路

• 核心目标: 在每次Union操作构建树时，尽可能让树不长高
• 实现方法:
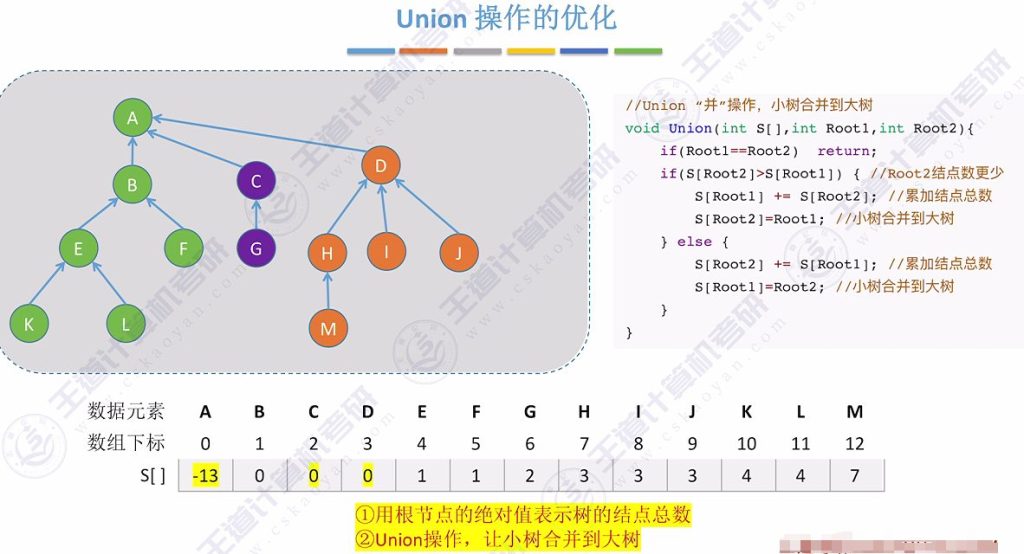
  • 用根节点的绝对值表示树的结点总数
  • Union操作时让小树合并到大树
• 具体实现:
  • 初始化数组元素为-1
  • Find操作时间复杂度最坏为O(n)
  • Union操作时间复杂度为O(1)

优化原理

• 合并策略:
  • 将结点数少的树合并到结点数多的树下
  • 避免让大树成为小树的子树导致高度增加
• 示例说明:
  • 假设一棵大树有多个结点，小树只有3个结点
  • 让小树成为大树的子树，合并后树高不变
  • 若反向合并，会导致树高增加

4.2 Union 操作的优化过程

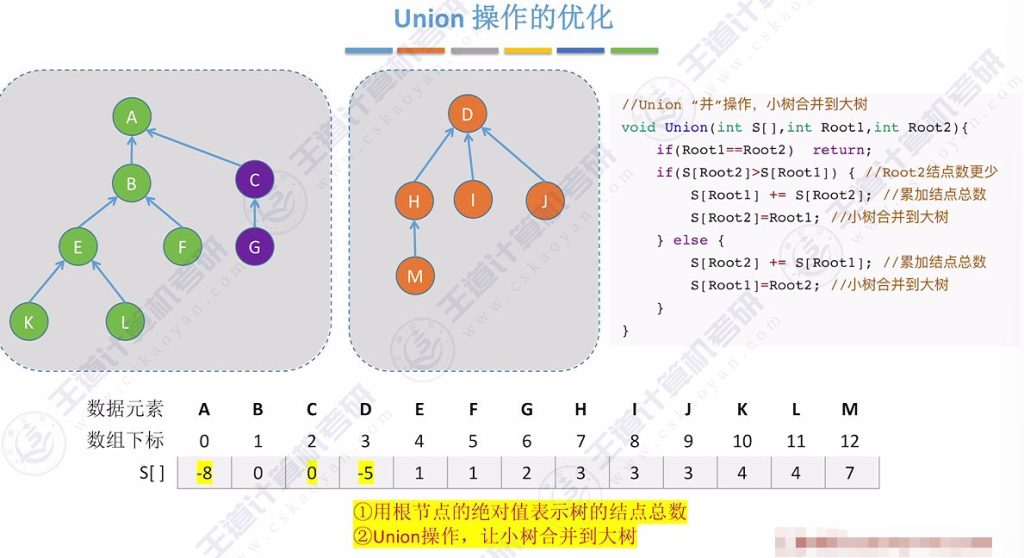
4.3 Union 操作的优化后的时间复杂度

• 结点总数表示:
  • 根节点存储负的结点总数，如-6表示6个结点
  • 通过比较绝对值判断树的大小
• 合并步骤:
  • 比较两棵树的结点数
  • 将小树的根指向大树的根
  • 更新大树的结点总数(两树结点数相加)
• 代码实现:
  • 使用if-else判断树的大小
  • 累加结点总数并修改指针

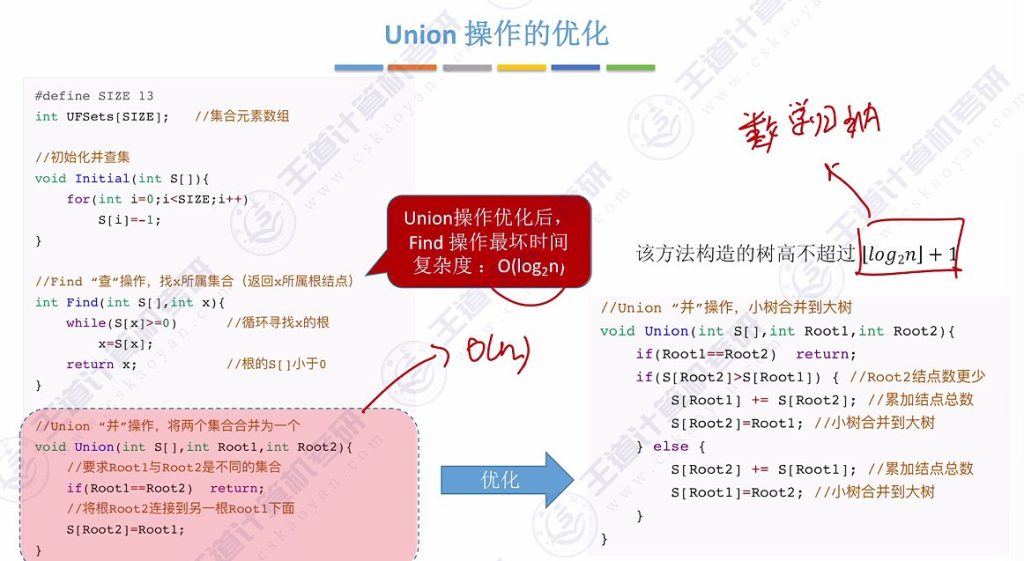
4）优化效果分析

• 树高限制:
  • 优化后树高不超过[log⁡2n]+1
• 时间复杂度:
  • Find操作最坏时间复杂度降为O(log⁡2n)
  • Union操作仍保持O(1)复杂度
• 对比未优化情况:
  • 未优化时树高可能达到n
  • Find操作最坏时间复杂度为O(n)

五、知识回顾与重要考点

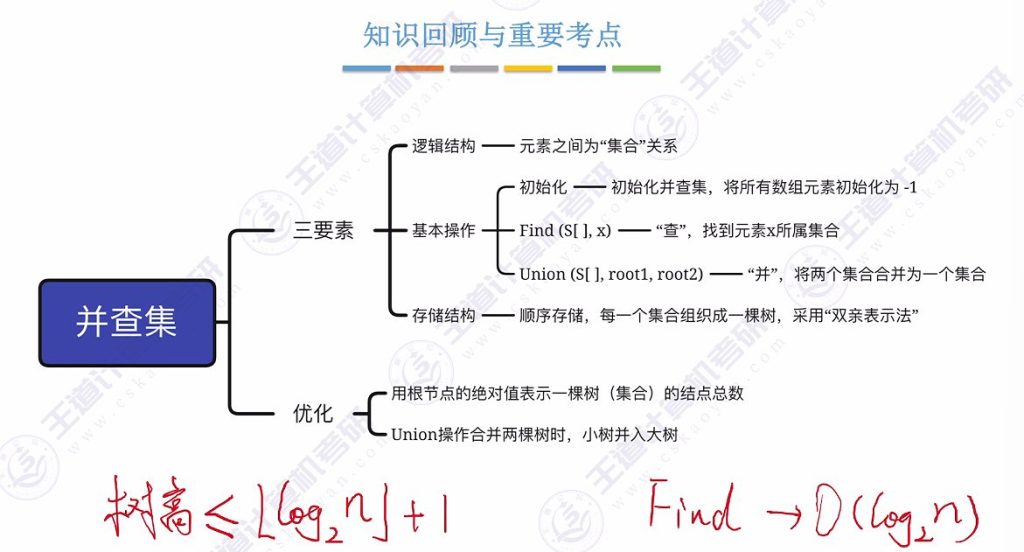
1）并查集三要素

• 逻辑结构:
  • 元素之间为”集合”关系
  • 两个元素要么同属一个集合，要么不属于
• 存储结构:
  • 顺序存储(数组实现)
  • 采用”双亲表示法”组织成树
• 基本操作:
  • 初始化：数组元素全置为-1
  • Find：查找元素所属集合(根节点)
  • Union：合并两个集合

2）优化要点

• 优化方法:
  • 用根节点绝对值表示集合大小
  • Union时小树合并到大树
• 优化效果:
  • 控制树高在O(log⁡n)级别
  • 提升Find操作效率
• 复杂度分析:
  • Find：O(log⁡n)
  • Union：O(1)

七、并查集的终极优化

7.1 并查集的进一步优化 – Find操作的优化（压缩路径）

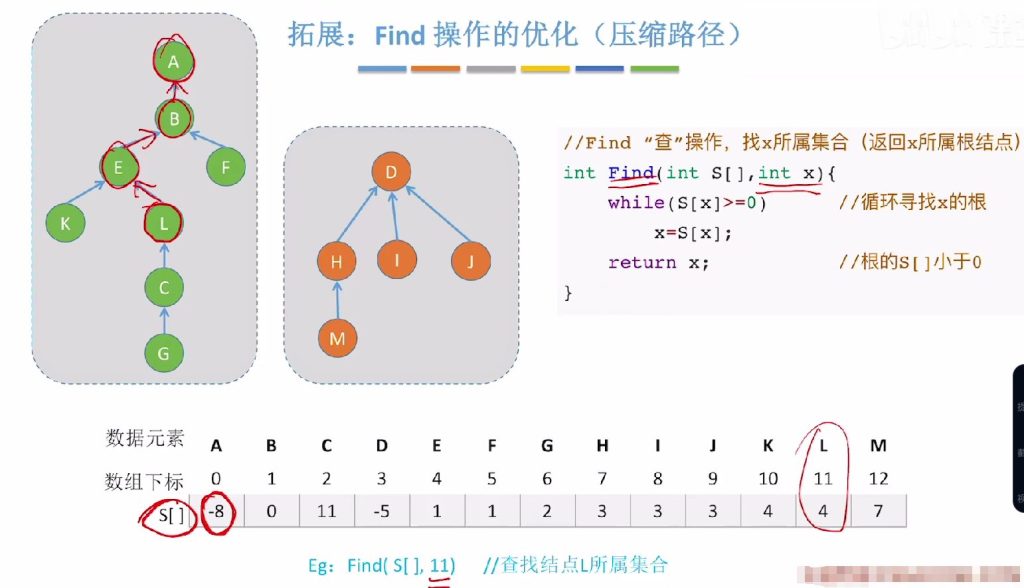
• 优化原理：在Find操作中先找到根节点，再将查找路径上所有结点都挂到根结点下，从而缩短后续查找路径
• 实现步骤：
  • 第一轮循环找到根节点（与基础Find操作相同）
  • 第二轮循环将路径上所有节点的父指针直接指向根节点

7.2 Find操作的优化（压缩路径） 代码实现

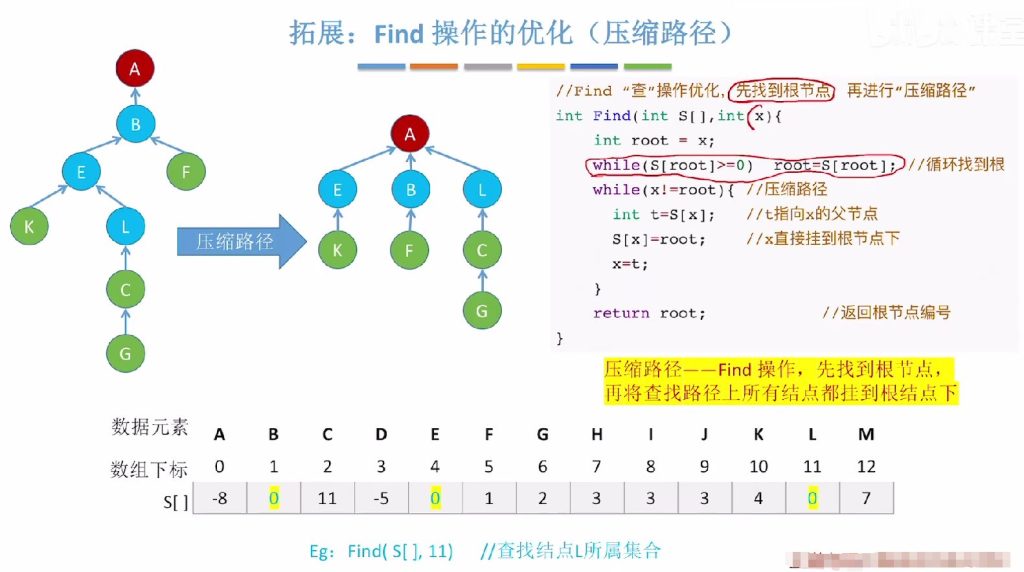
• 示例分析：查找结点L(11)时，原路径L→E→B→A被压缩为L→A、E→A，B保持原样
• 时间复杂度：优化后树高不超过O(α(n))，其中α(n)是增长极慢的函数，常见n值下α(n)≤4

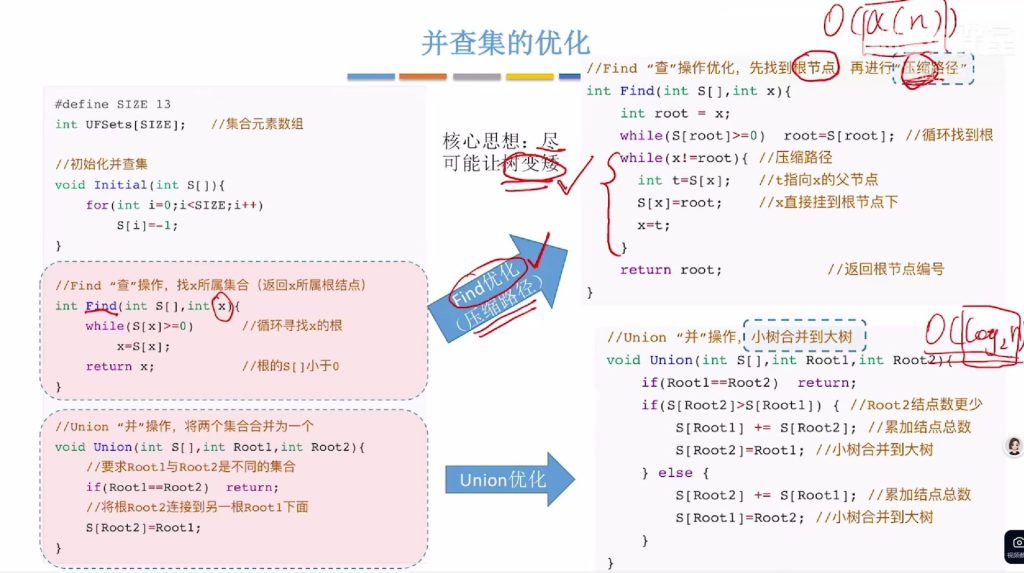
7.3 并查集的整体优化

7.4 并查集优化的总结

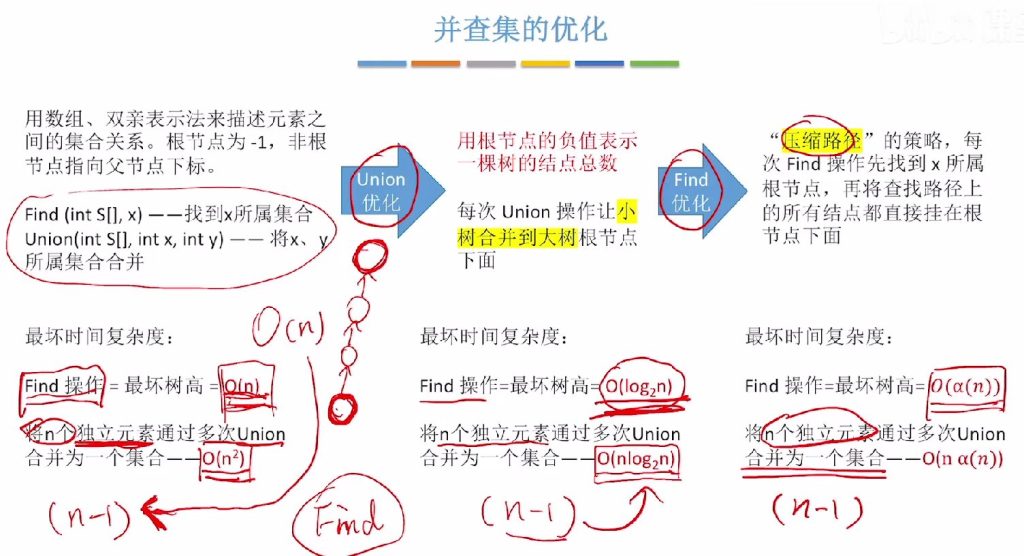
• Union优化：
  • 策略：让结点数少的树合并到结点数多的树下（小树合并到大树）
• Find优化：
  • 策略：压缩路径，使查找路径上的节点直接指向根
• 核心思想：所有优化都围绕”尽可能让树变矮”展开，降低Find操作的最坏时间复杂度