一、知识总览
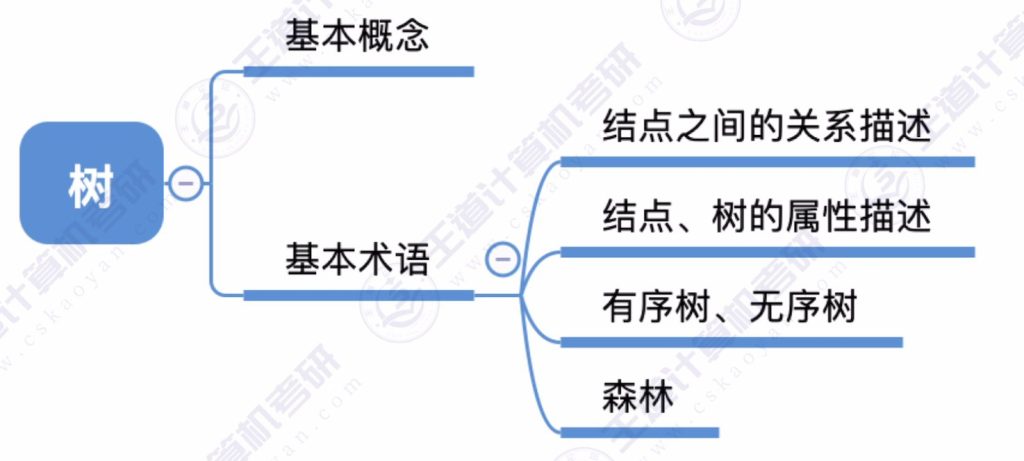
二、树的定义和基本术语
2.1 树的基本概念
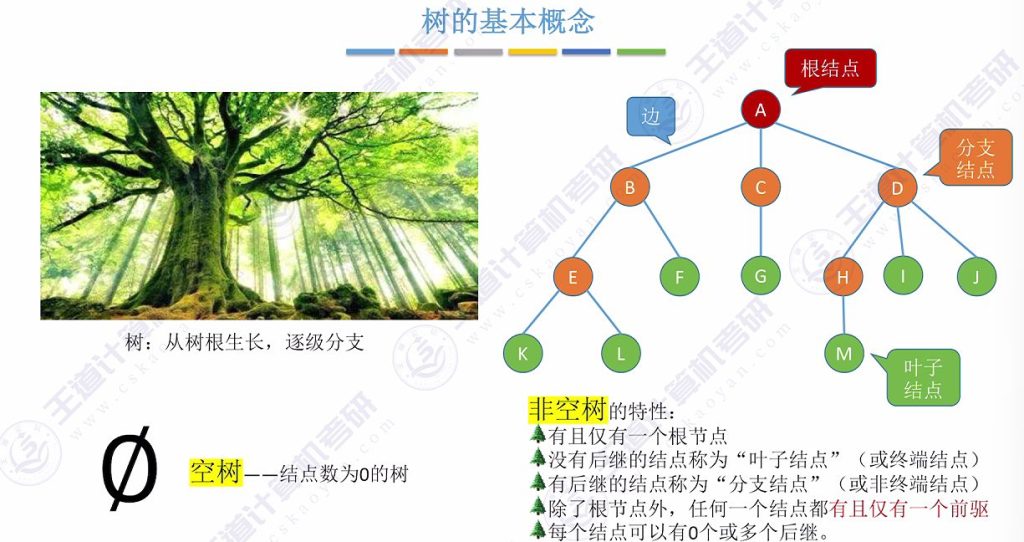
两种形态:空树、非空树
前驱后继:根结点无前驱,叶子结点无后继;分支结点=非终端结点,叶子结点=终端结点
唯一前驱:除根结点外,每个结点有且仅有一个前驱(多前驱则变为图结构)
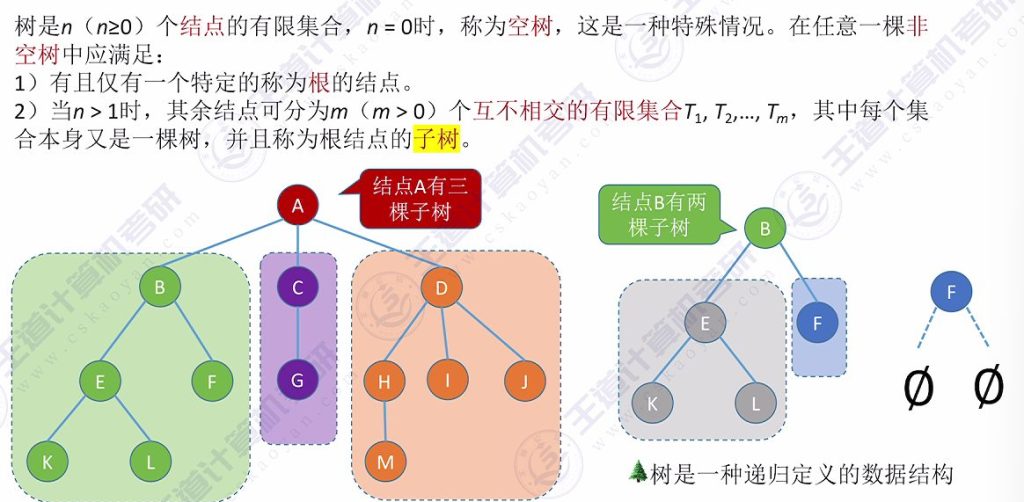
树是一种递归定义的数据结构
子树特性:子树本身也是树,且各子树必须互不相交(对应唯一前驱约束)
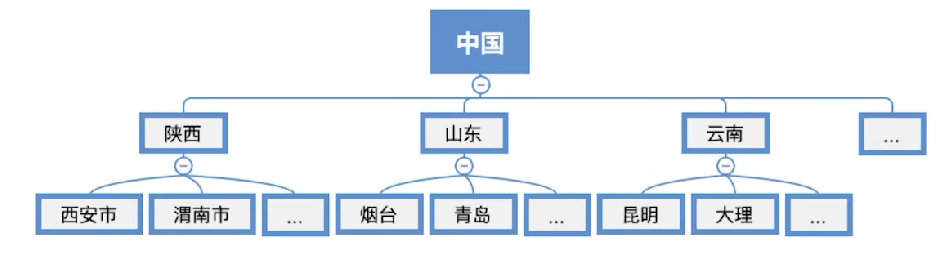
2.2 树形逻辑结构的应用
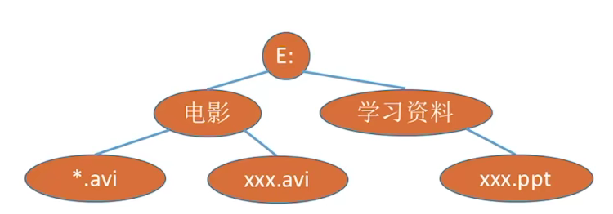
2.3 结点之间的关系描述
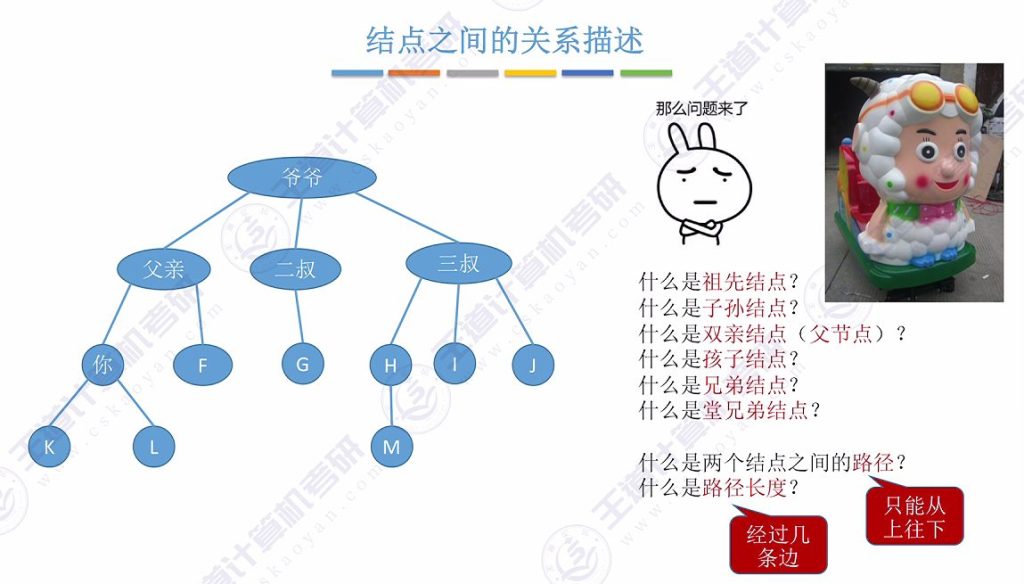
- 祖先/子孙:从结点到根路径上的所有结点为祖先;结点分支下的所有结点为子孙
- 双亲/孩子:直接前驱为双亲结点(父结点),直接后继为孩子结点
- 兄弟/堂兄弟:同父结点为兄弟;同层不同父为堂兄弟(考试中”堂兄弟”多指同层关系)
- 路径特性:路径只能从上往下单向,路径长度=经过的边数(如爷爷到孙子路径长度为2)
2.4 结点、树的属性描述
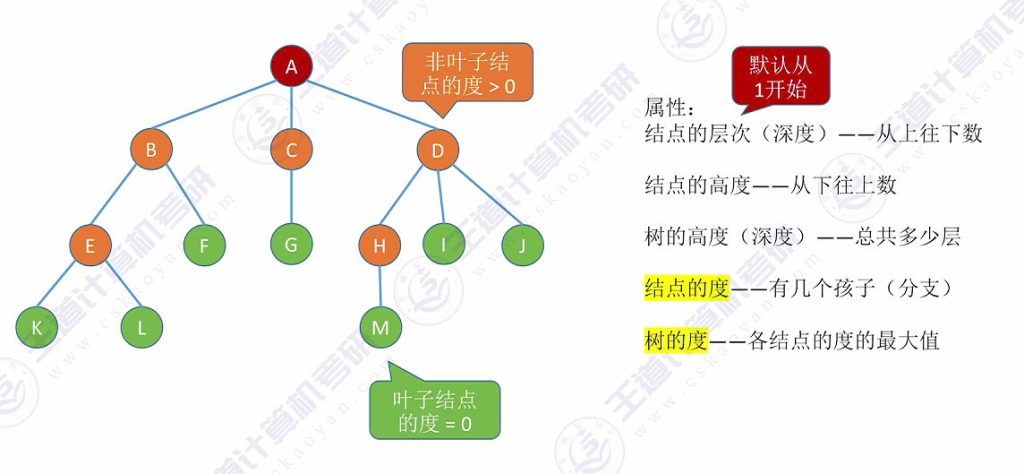
- 层次/深度:从上往下计数(默认从1开始,部分教材从0开始)
- 高度:从下往上计数(最底层为1)
- 结点度:结点的分支数(叶子结点度=0,如m、i、j结点)
- 树的度:树中所有结点度的最大值(示例中树的度为3)
- 重要考点:结点度和树的度是考题高频考点,影响树的结构特性分析
2.5 有序树 VS 无序树
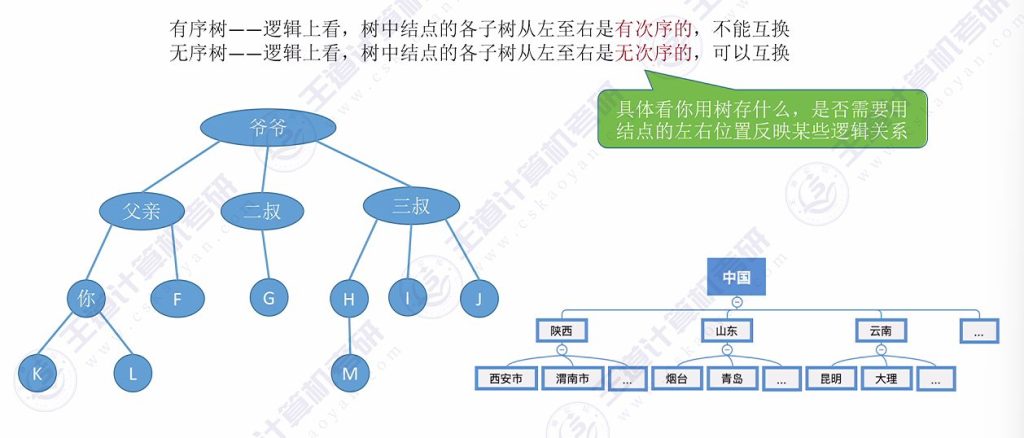
- 有序树:子树有严格左右次序(如家谱按出生顺序排列,交换会改变语义)
- 无序树:子树可任意交换位置(如行政区划分无顺序要求)
- 判断依据:取决于是否需要用结点位置表达逻辑关系
2.6 树和森林
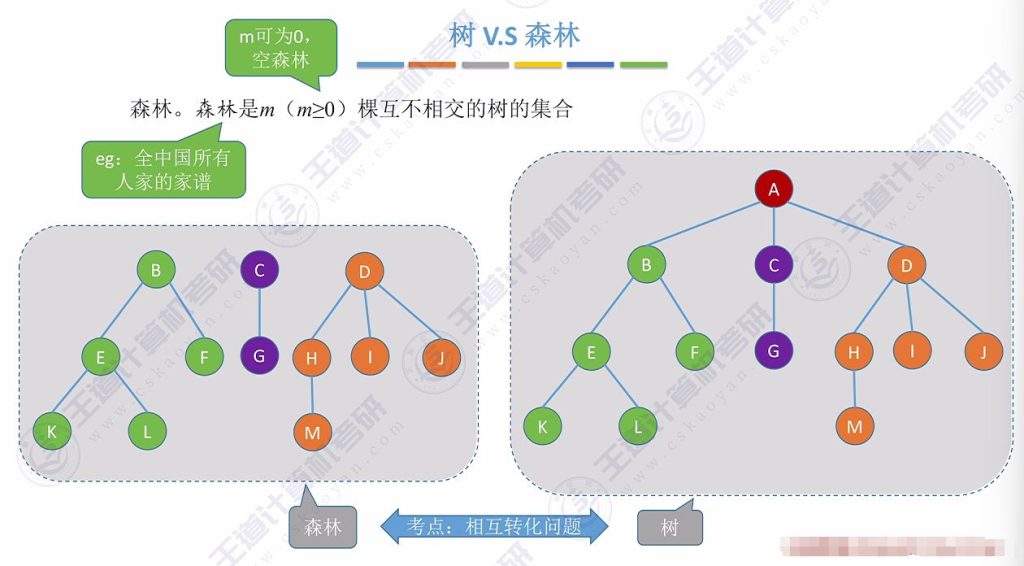
- 森林定义:m (m≥0)棵互不相交树的集合(允许空森林m=0)
- 转换关系:添加根结点可将森林合并为树;删除根结点可将树拆分为森林
- 应用场景:全国家谱系统(不同家族树互不相交)、文件系统多级目录
重要考点:森林和树相互转换问题
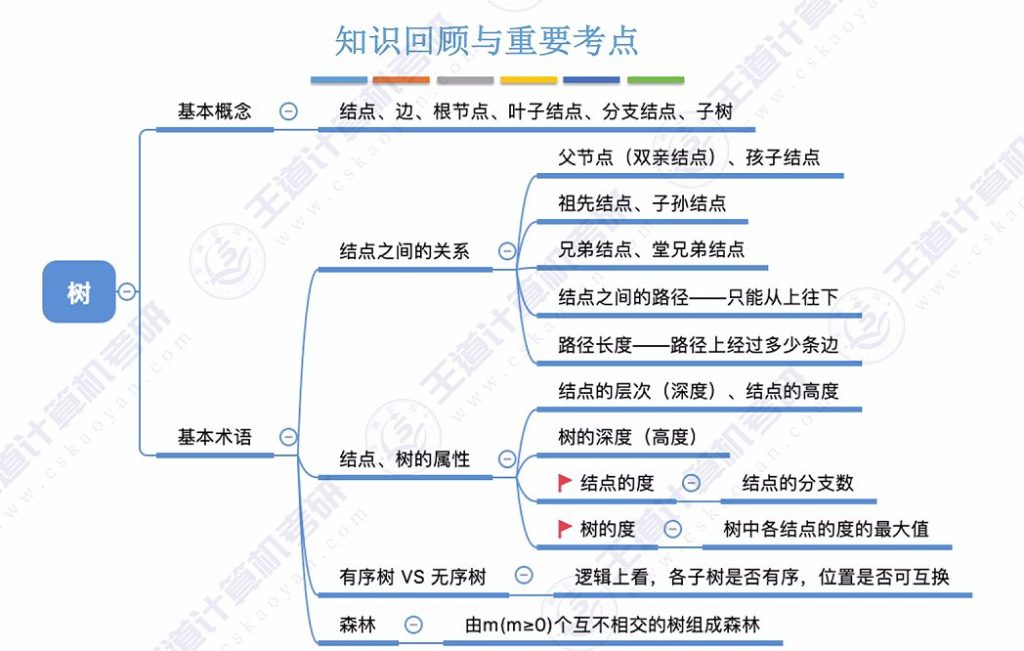
2.7 树的知识回顾
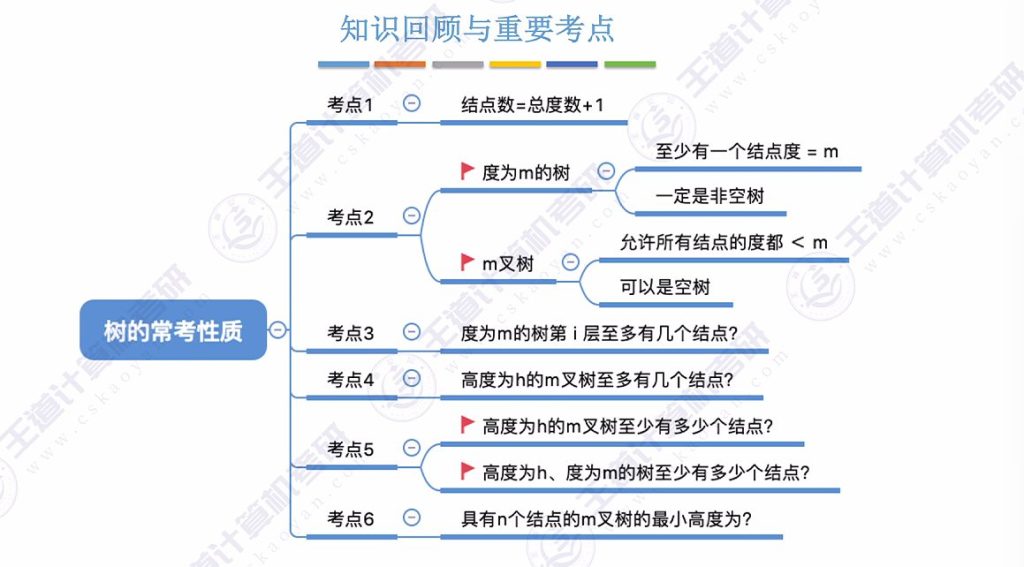
三、树的常考性质
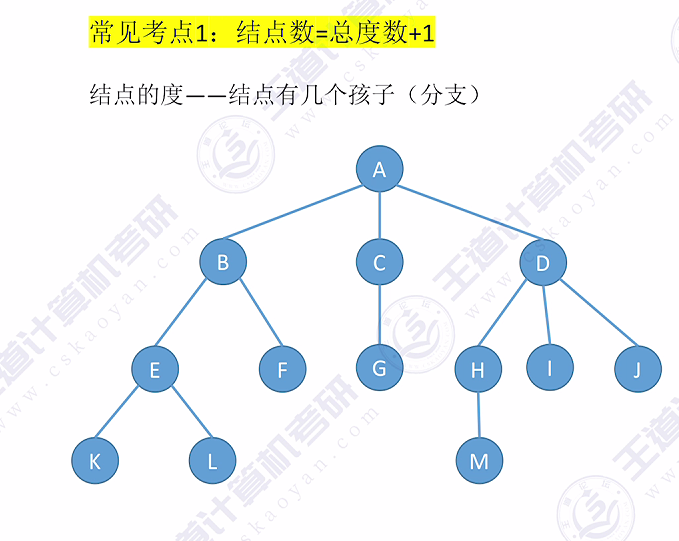
3.1 性质1
结点数与总度数的关系: 结点数 = 总度数 + 1
结点的度指的是结点有几个孩子(分支),每个分支下都会连一个孩子。
根节点头上没有“天线”(即没有父节点指向它),所以总结点数时需要在总度数基础上加一。
3.2 性质2
常见考点2:度为m的树、m叉树的区别
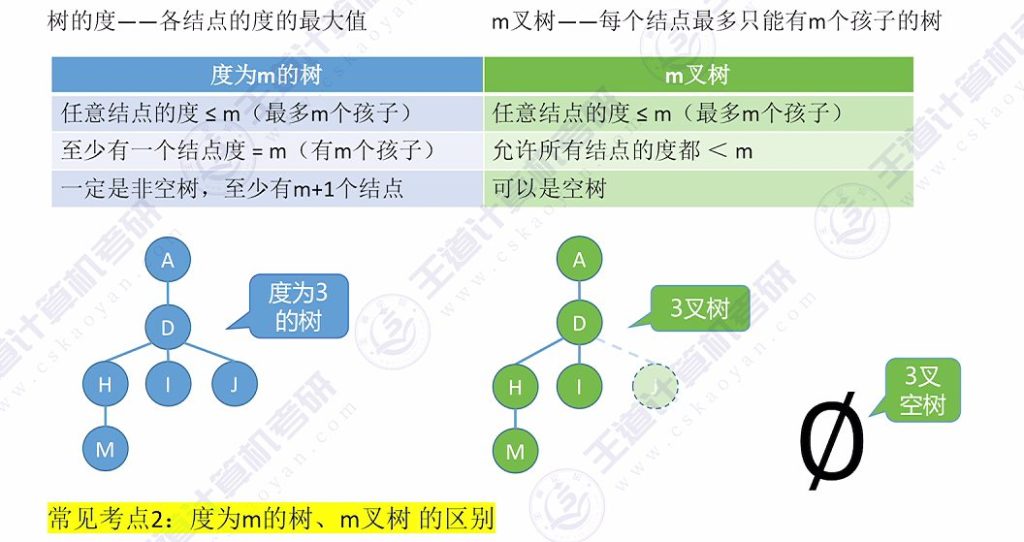
- 度为m的树: 树中至少有一个结点的度数为m,一定是非空树,且至少有m+1个结点(根结点加上m个孩子)。
- m叉树: 每个结点最多只能有m个孩子,允许所有结点的度都小于m,可以是空树。
3.3 性质3
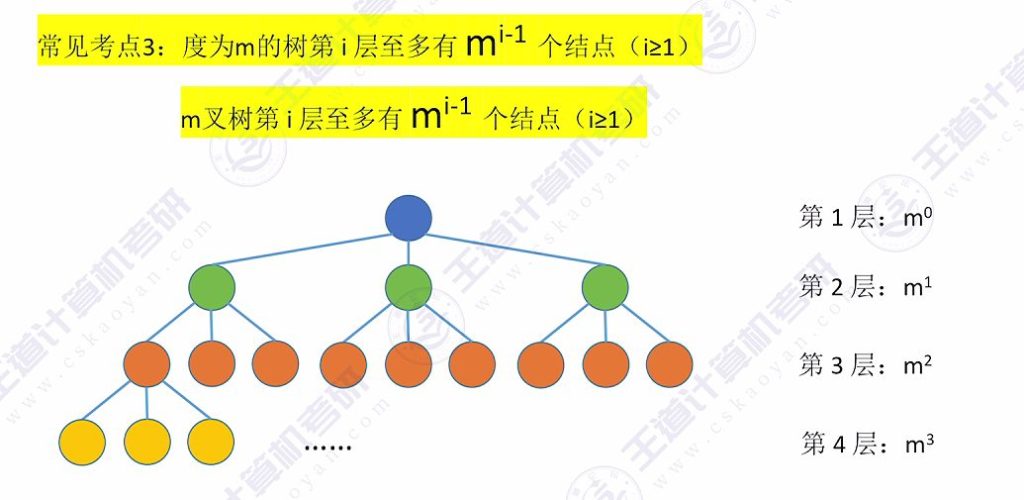
根结点(第1层)只有一个,每层结点最多有m个孩子,因此第i层结点数至多为

3.4 性质4 – 对于高度为h的m叉树
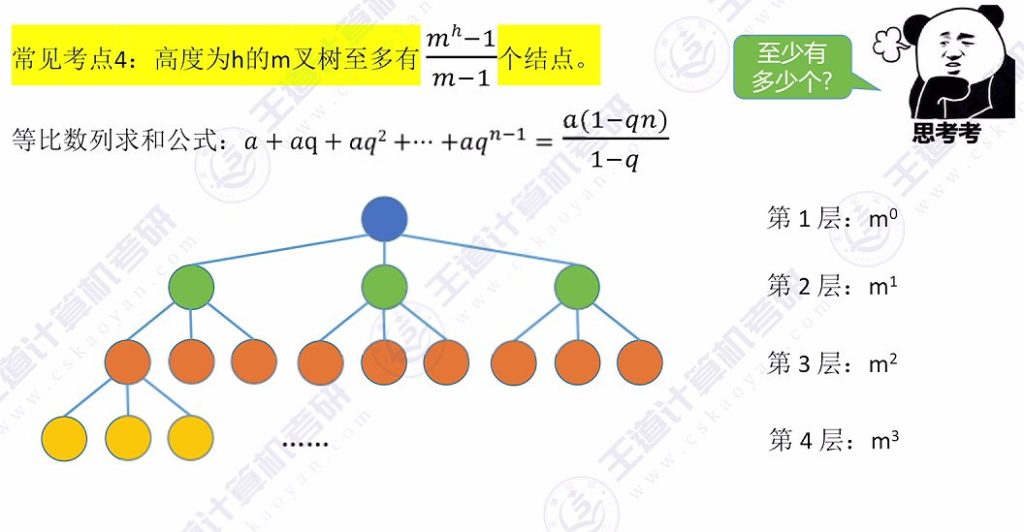
方法: 使用等比数列求和公式计算,每层结点数构成等比数列。
3.5 性质5
- 高度为h的m叉树至少结点数: 高度为h的m叉树至少有h个结点。
- 高度为h、度为m的树至少结点数: 高度为h、度为m的树至少有h+m-1个结点。

解释: m叉树最少结点数情况为从根结点一直往下,每个结点只有一个孩子;度为m的树至少要保证有一个结点有m个孩子。
3.6 性质6

- 方法: 为了让树的高度最小,需要让每个结点尽可能有最多的孩子(即m个孩子),这样树会往宽处长而不是往高处长。
- 注意是向上取整的符号
3.7 知识回顾
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


