一、二叉树的基本概念
1.1 二叉树的基本概念知识总览
1.2 二叉树的基本概念
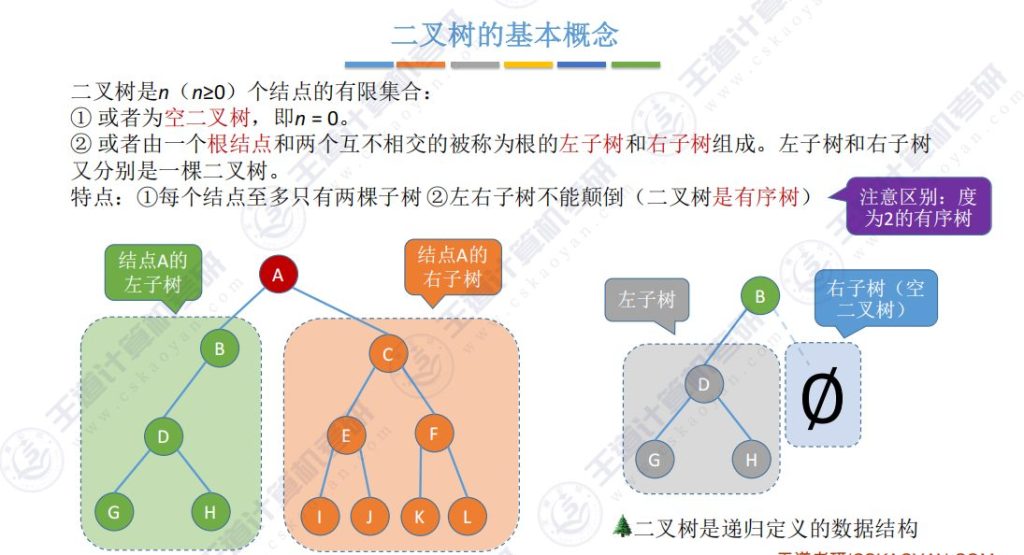
- 递归定义:二叉树是n(n≥0)个结点的有限集合,要么为空树(n=0),要么由根结点和两个互不相交的左右子树组成
- 核心特性:
- 最大分支数:每个结点至多只有两棵子树
- 有序性:左右子树不能颠倒(区别于度为2的有序树)
- 与度为2树的区别:二叉树允许空树存在,且必须明确区分左右子树顺序
1.3 二叉树的五种状态
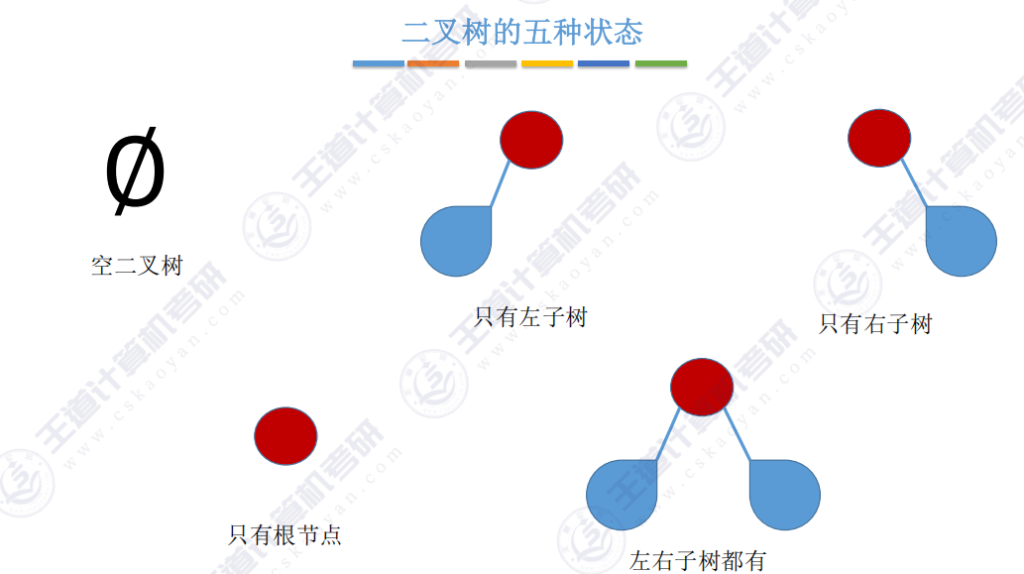
- 空二叉树:不含任何结点
- 仅有左子树:右子树为空二叉树
- 仅有右子树:左子树为空二叉树
- 仅根结点:左右子树均为空二叉树
- 完整形态:左右子树均非空
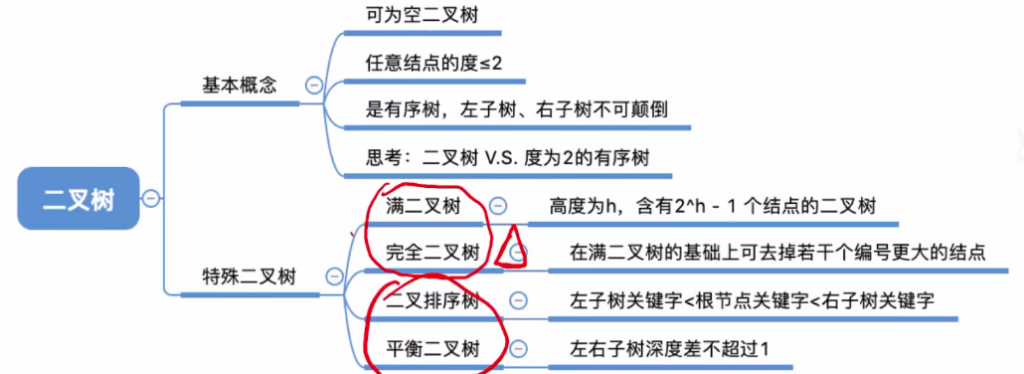
1.4 几种特殊的二叉树 – 满二叉树
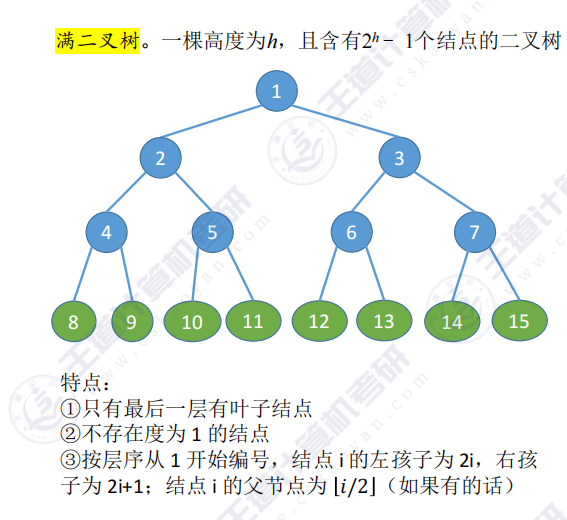
- 严格定义:高度为h且含有2h−1个结点的二叉树
- 三大特征:
- 叶子分布:只有最后一层有叶子结点
- 结点度数:不存在度为1的结点(只有0或2度)
- 编号规律:按层序编号时,结点i的左孩子为2i,右孩子为2i+1,父结点为【i/2】向下取整
编号规律有助于用顺序存储的方式来存储结点
1.5 几种特殊的二叉树 – 完全二叉树
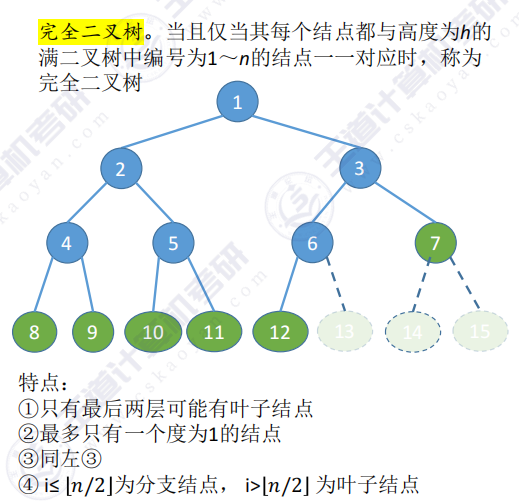
- 定义本质:结点编号与同高度满二叉树中1∼n编号完全对应
- 关键特性:
- 叶子分布:最后两层可能出现叶子结点
- 度数限制:最多只有一个度为1的结点
- 孩子规律:若有单个孩子则必为左孩子
- 存储特性:继承满二叉树的编号计算规则(按层序编号时,结点i的左孩子为2i,右孩子为2i+1,父结点为【i/2】向下取整)
- 结点分类:当i≤[n/2]时为分支结点,反之为叶结点
满二叉树肯定是完全二叉树
但是完全二叉树未必是满二叉树
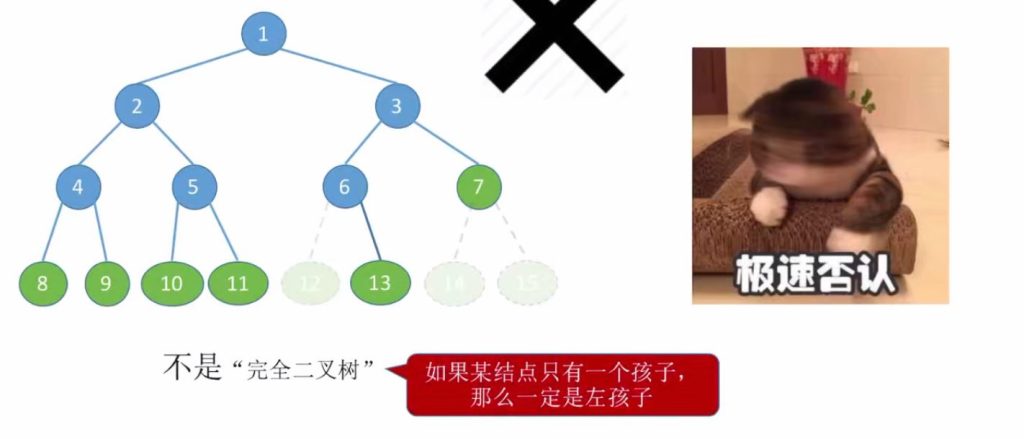
1.6 几种特殊的二叉树 – 二叉排序树(重要)
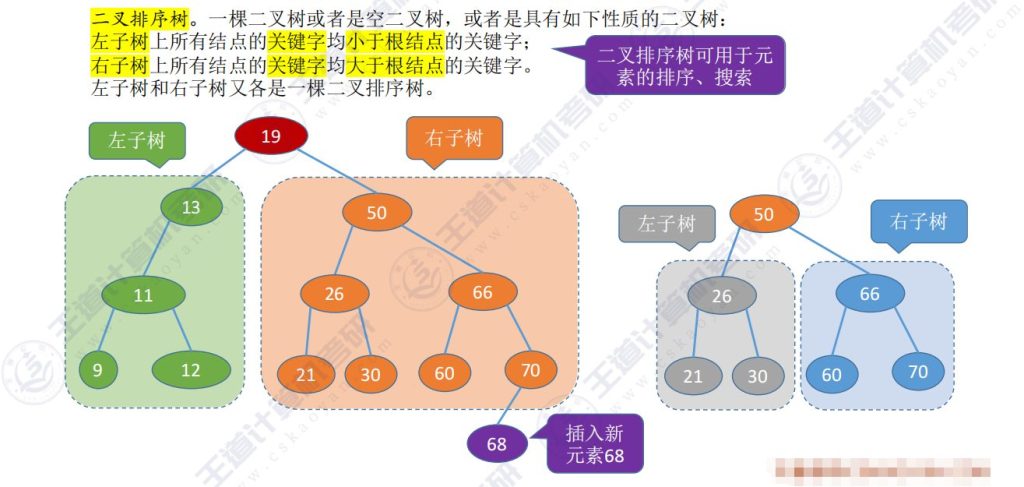
- 排序规则:
- 左子树所有结点关键字 < 根结点关键字 < 右子树所有结点关键字
- 左右子树本身也是二叉排序树
- 操作优势:
- 查找效率:通过大小比较可快速定位目标结点(如查找60的演示过程)
- 插入方法:新结点68按比较规则插入适当位置,保持排序性质
1.7 几种特殊的二叉树 – 平衡二叉树
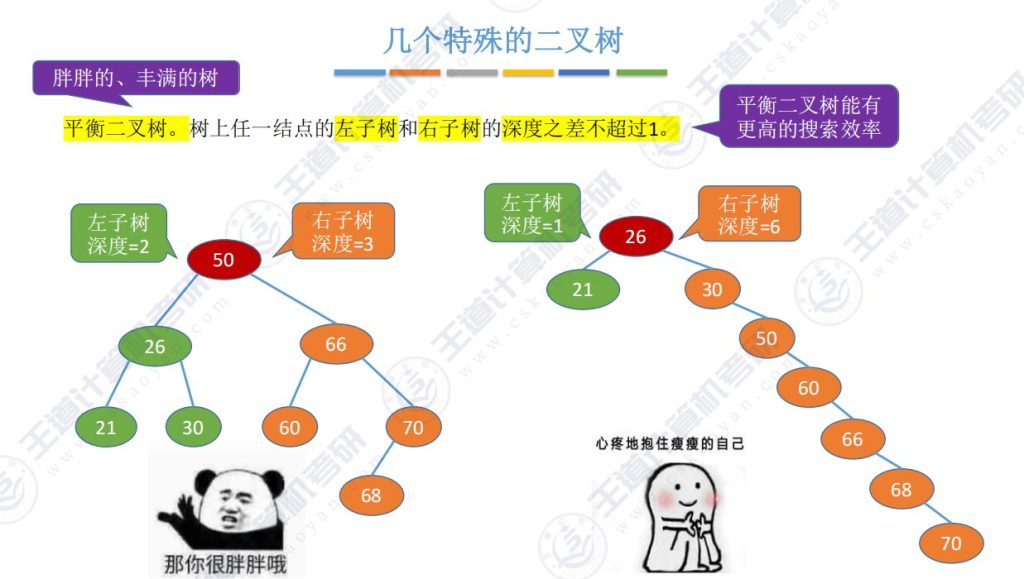
- 平衡条件:任意结点左右子树深度(高度)差不超过1
- 性能优势:
- 搜索效率:平衡状态下查找70仅需2步,非平衡状态需要多步
- 形态特征:”胖”树结构(高度低)优于”瘦”树结构(高度高)
- 与二叉排序树关系:平衡二叉树可优化二叉排序树的查询性能
1.8 二叉树基本知识回顾
二、二叉树的常考性质
2.1 性质1 – 非空二叉树结点关系
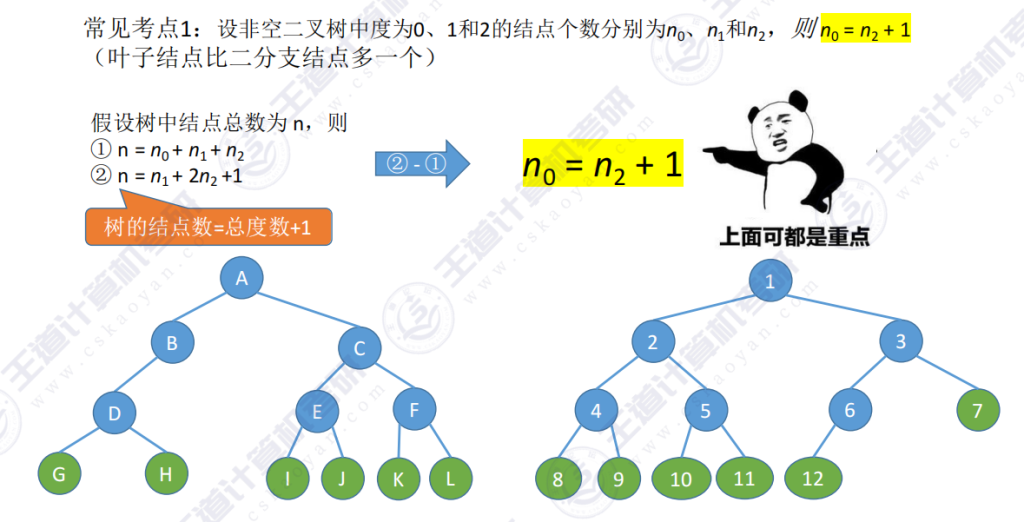
应用场景:该结论在选择题中出现频率极高,可通过示例二叉树验证(如ABDEFGIJKLM结构)
- 叶子结点比二分支结点多一个
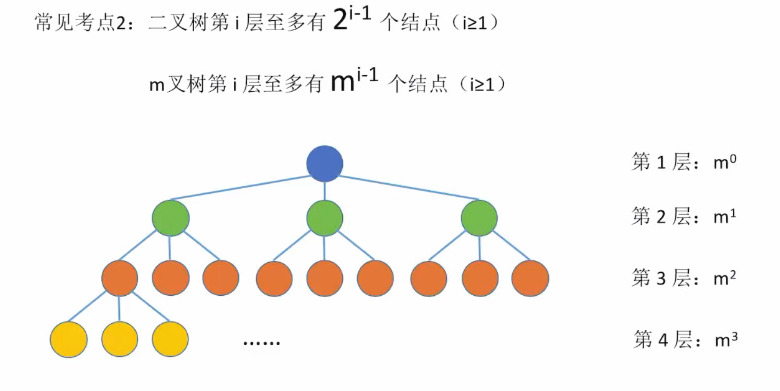
2.2 性质2 – 二叉树第 i 层结点数
2.3 性质3 – 高度为 h 的二叉树结点数
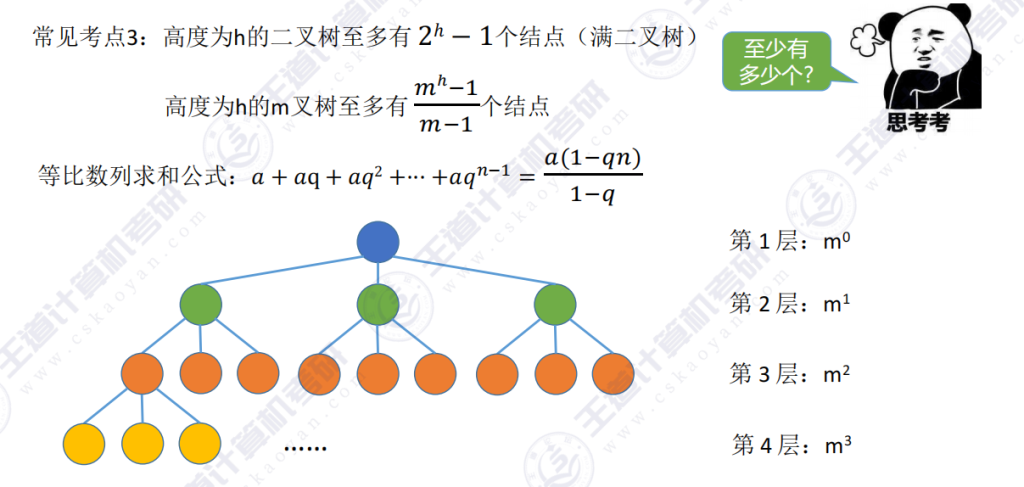
三、完全二叉树的常考性质
3.1 完全二叉树的高度
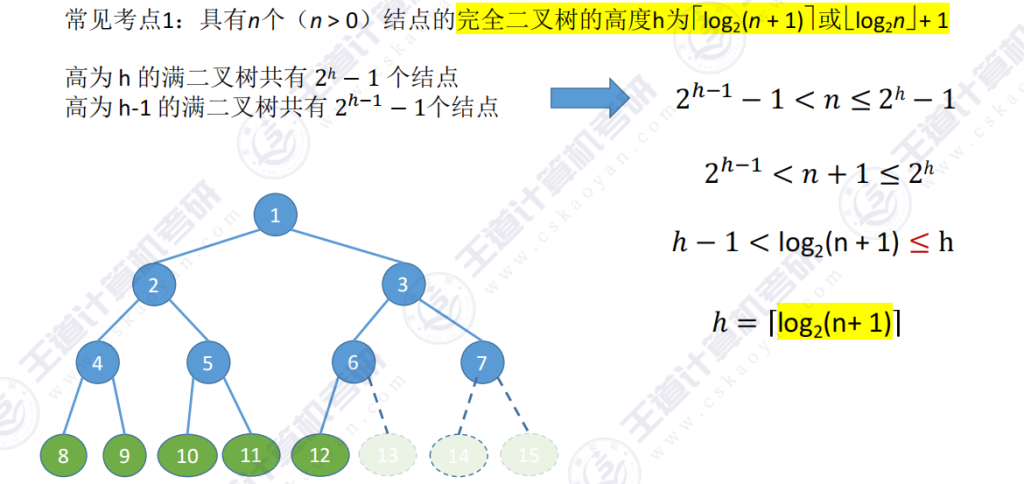
- 向上取整
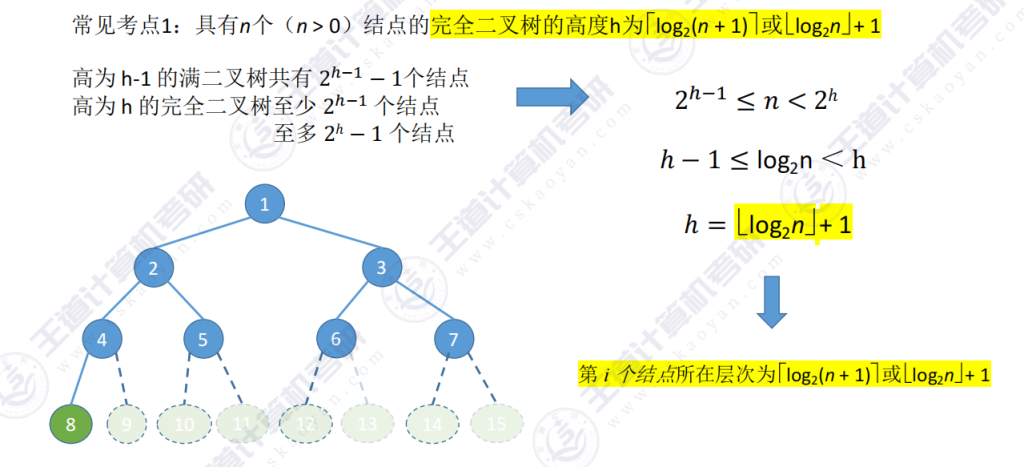
- 向下取整
推导



3.2 完全二叉树的度结点计算
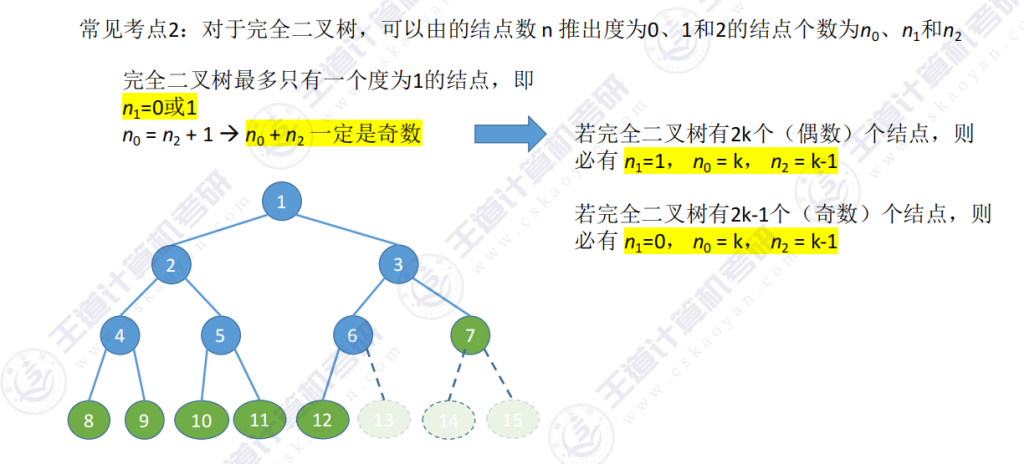
n0 – 度为0,也就是叶子结点
n1 – 度为1,上一层有左孩子、没右孩子的结点,完全二叉树最多只有一个度为1的结点
n2 – 度为2
结论:
1、若完全二叉树有2k个(偶数)结点,则必有n1 = 1, n0 = k, n2 = k – 1
2、若完全二叉树有2k – 1 结点,则n1=0;n0 = k; n2= k-1;
3.3 结论小节

四、二叉树的存储结构
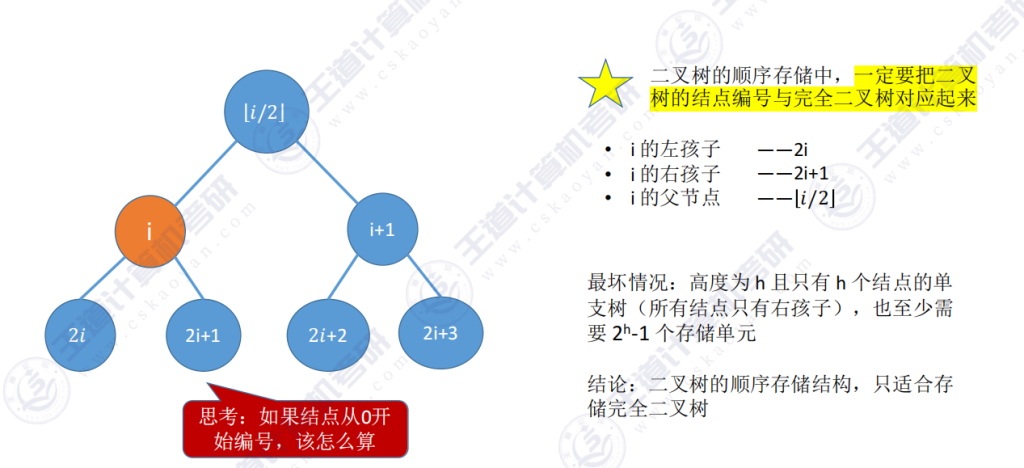
4.1 二叉树的顺序存储
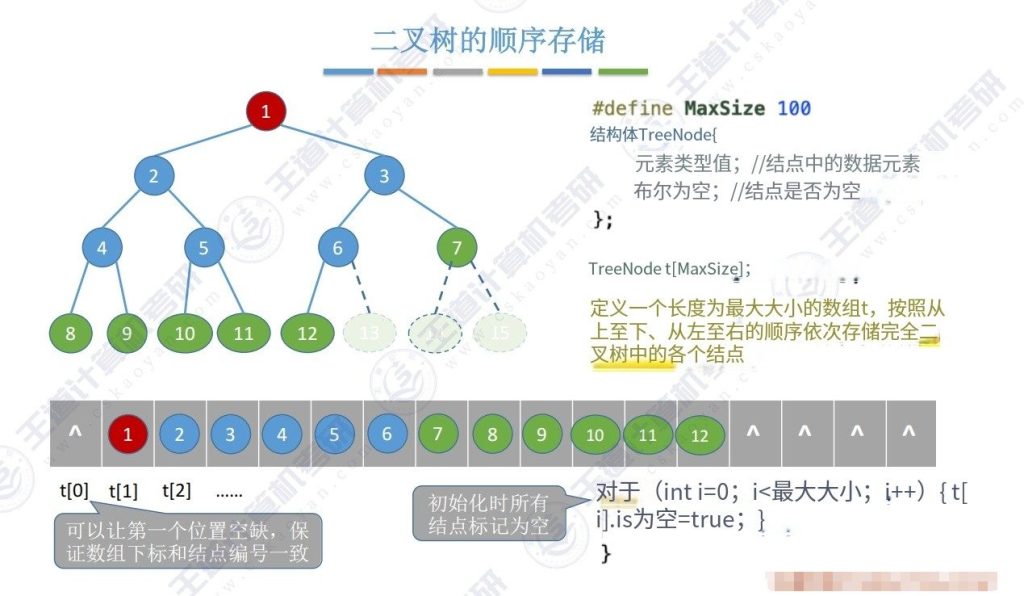
- 实现方式:将二叉树节点按层序编号后,连续存储在数组中。数组下标与节点编号一致(通常从1开始)。
- 初始化:所有节点的isEmpty初始设为true,表示空节点状态。
4.2 二叉树顺序存储的基本操作
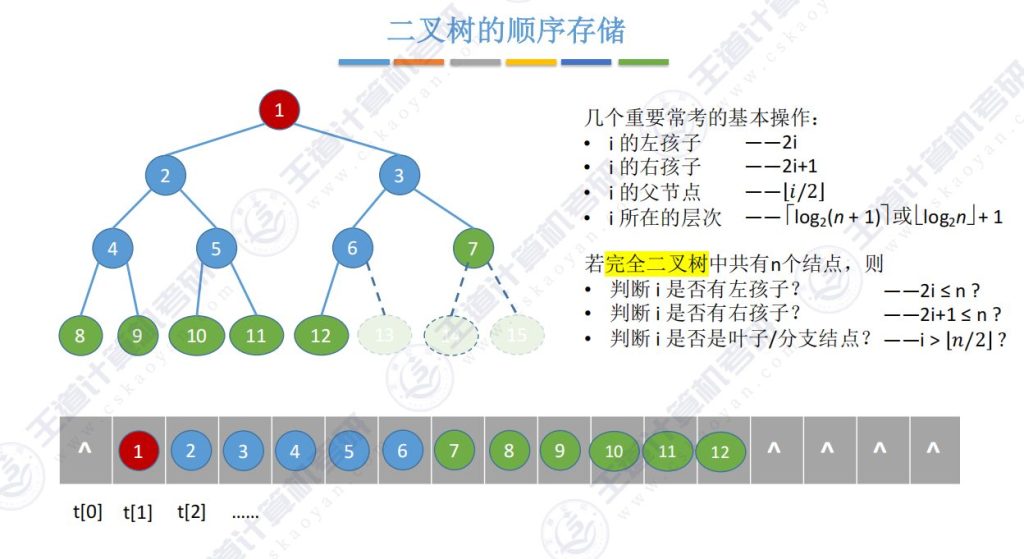
i 是结点编号或数组下标反映关系

4.3 顺序存储 – 非完全二叉树处理
如果不是完全二叉树依然按层序将各节点顺序存储,那么无法从结点编号反映出结点间的逻辑关系
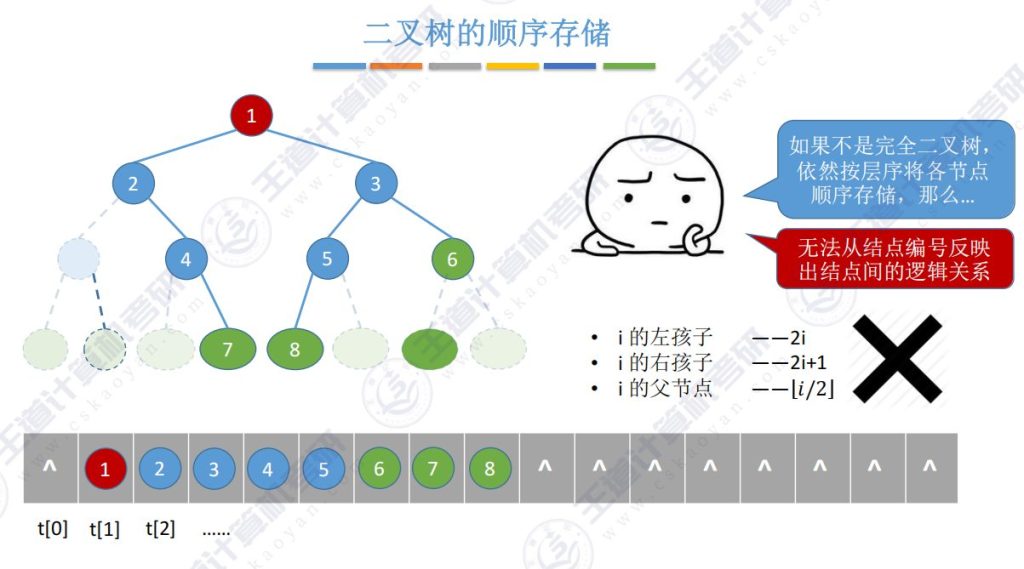
处理方法:二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来,即需补充虚拟节点使其成为完全二叉树结构
1、判断子节点存在性需检查isEmpty字段,如但是检查 2i 这个位置的结点,is empty判断应该是true,也就是空,那么就说明5号结点是不存在左孩子的。
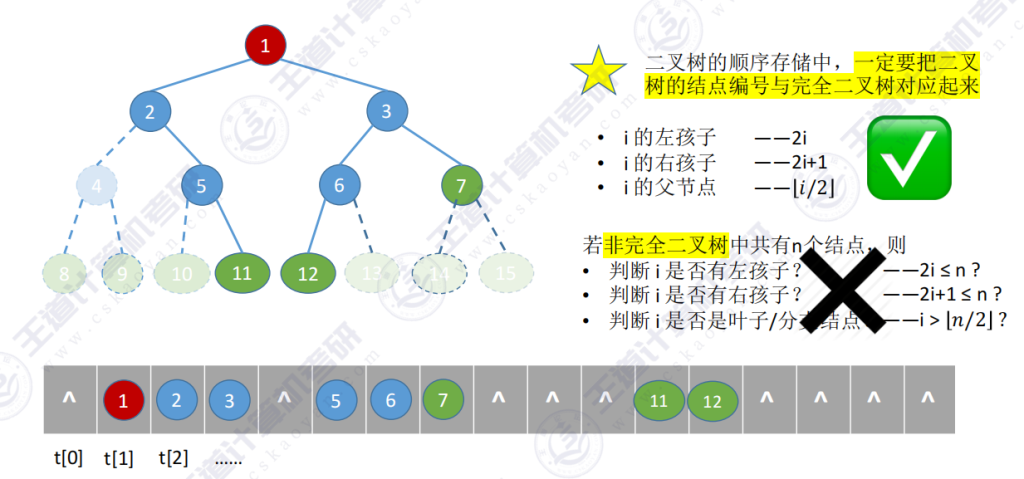
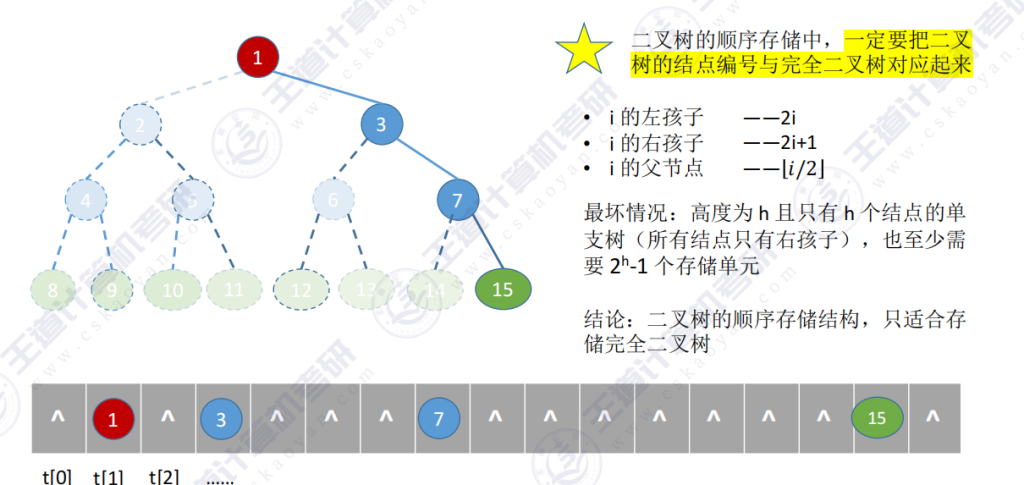
顺序存储方式仅适合存储完全二叉树,实际应用较少
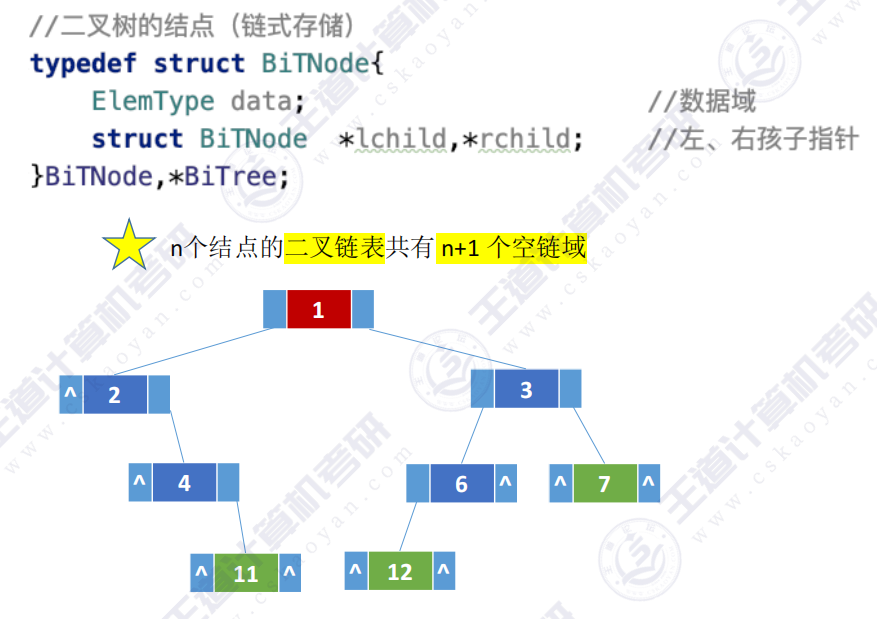
4.4 二叉树的链式存储
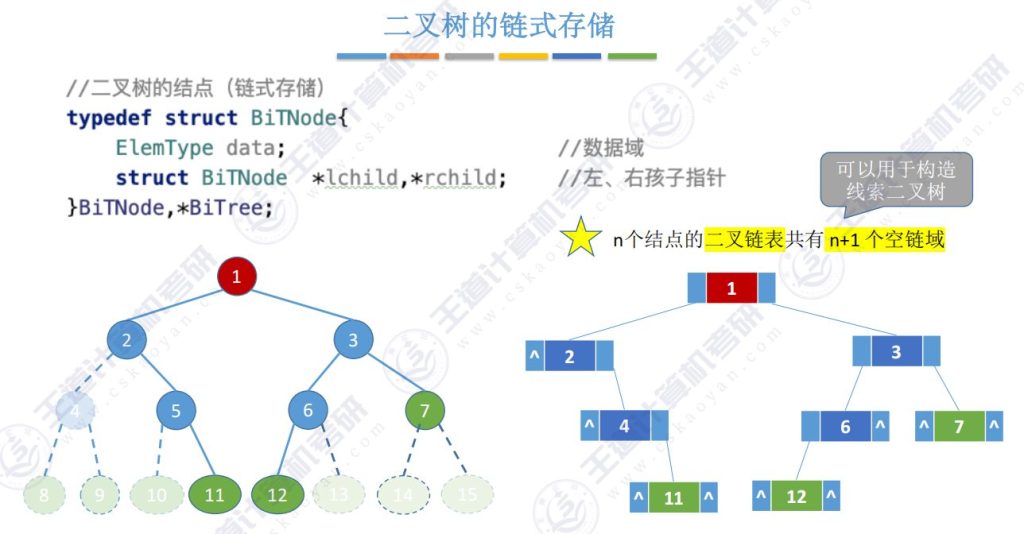
- 特性:
- n个节点的二叉链表共有2n个指针域
- 除根节点外每个节点被一个指针指向,也就是说n个结点的二叉链表共有n+1个空链域
(空指针域可用于构造线索二叉树)
4.5 二叉树的链式存储(算法实现)
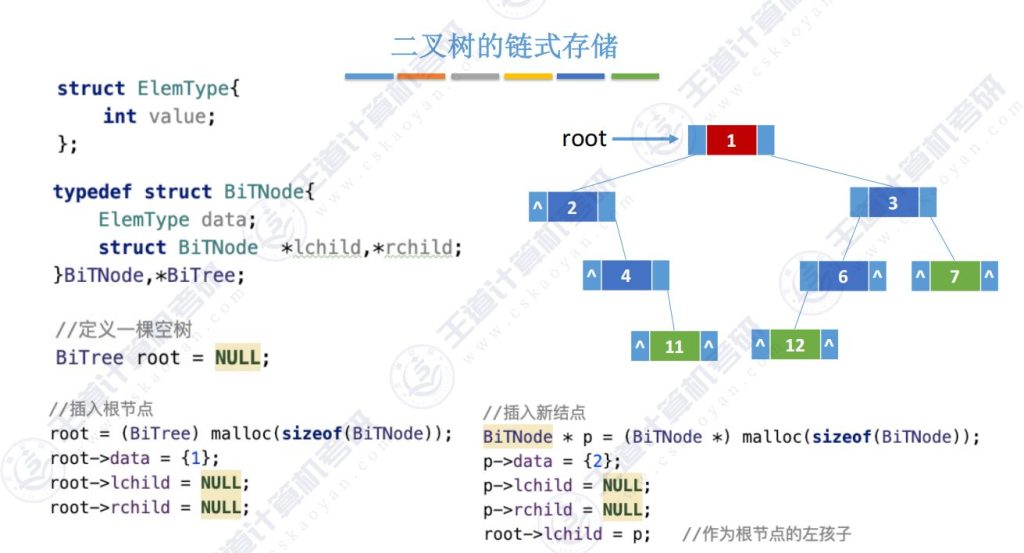
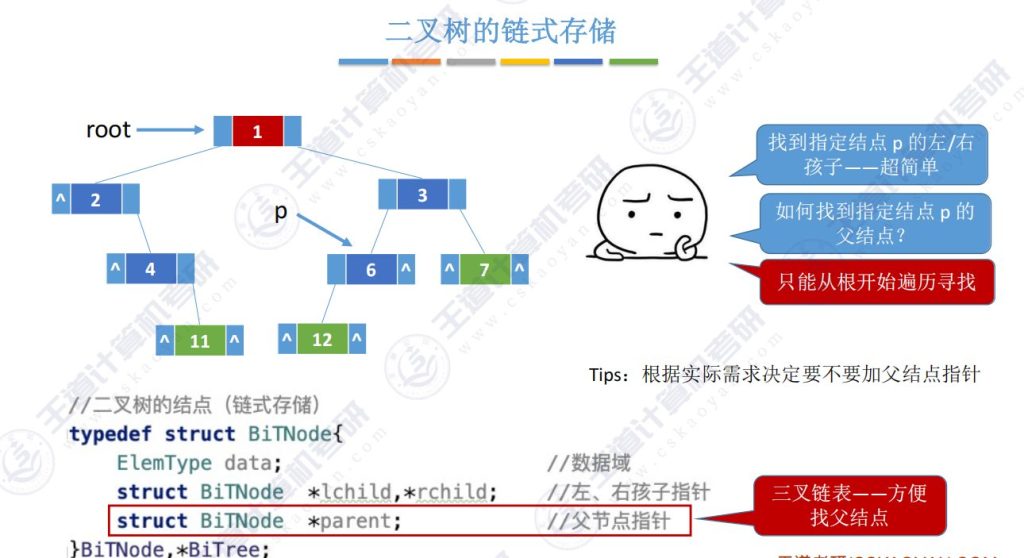
二叉树的链式存储方式寻找结点p的左孩子和右孩子结点非常简单
但是对于寻找父结点需要从根结点遍历,对于经常需要寻找父节点的情况,使用三叉链表
- 操作复杂度:
- 查找孩子节点:O(1
- 查找父节点:O(n)(无parent指针时需遍历)
考研中喜欢考不带父指针的情况
4.6 知识回顾
- 结论
- 顺序存储:仅适用于完全二叉树
- 链式存储:通用性强,空间利用率高
- 三叉链表:频繁需要父节点访问的场景
五、二叉树的遍历(先序、中序、后序)
5.1 什么是遍历
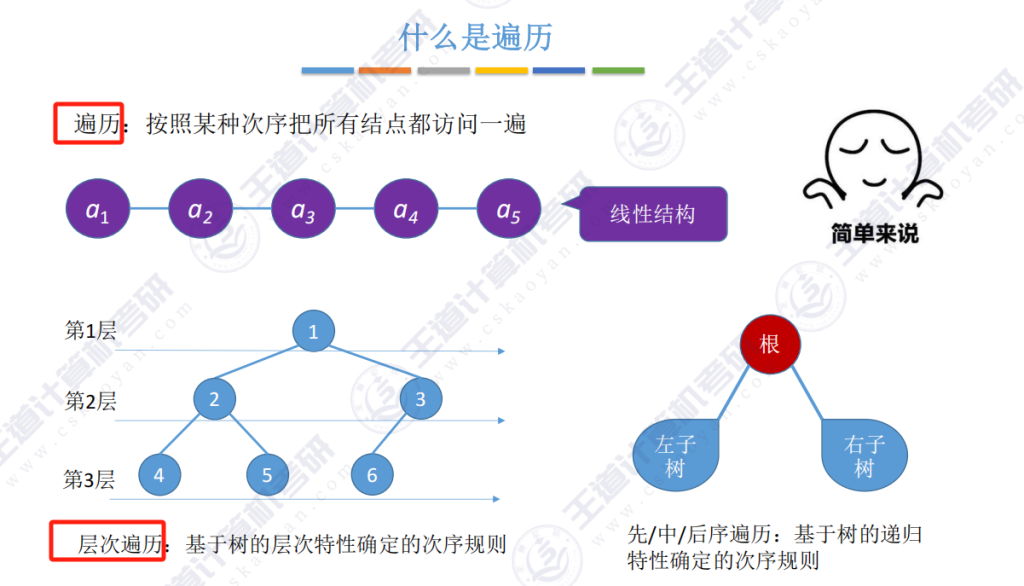
- 基本概念:按照某种次序把所有结点都访问一遍
- 线性结构:顺序简单,可从头到尾或从尾到头遍历
- 树形结构:利用分层特性制定遍历规则,如层次遍历
- 递归特性:基于”根节点+左子树+右子树”的递归结构制定遍历规则
5.2 二叉树 3 种遍历的概念
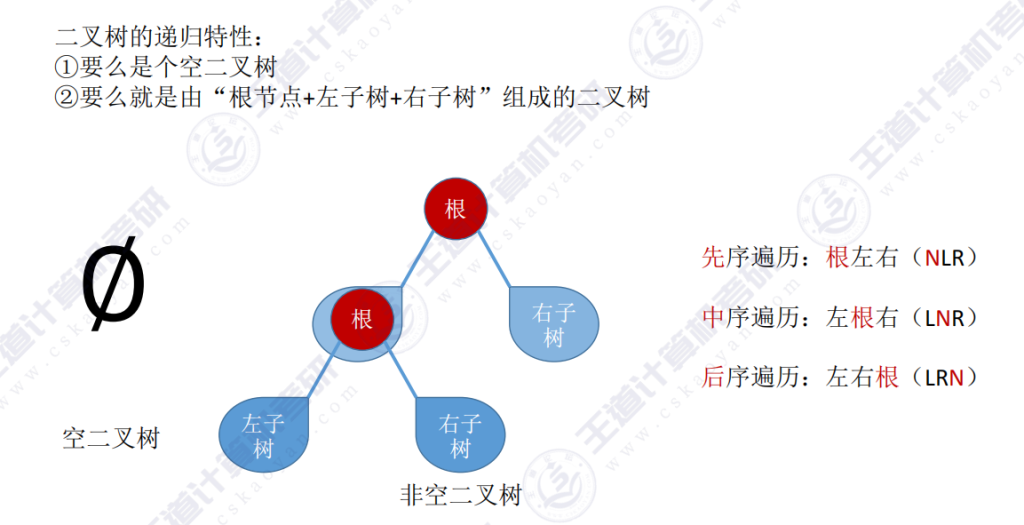
1)如果是空二叉树,则什么都不用操作;
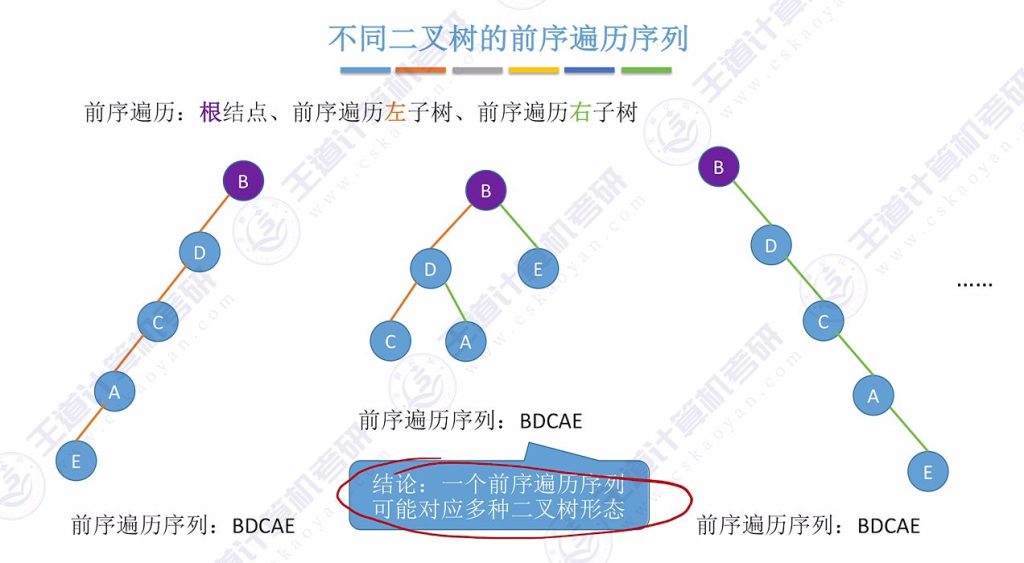
2)求先序遍历序列
- 规则:根左右(NLR)
- 递归过程:
- 访问根节点
- 递归先序遍历左子树
- 递归先序遍历右子树
3)求中序遍历序列(中根遍历)
- 规则:左根右(LNR)
- 别名:中根遍历
- 递归过程:
- 递归中序遍历左子树
- 访问根节点
- 递归中序遍历右子树
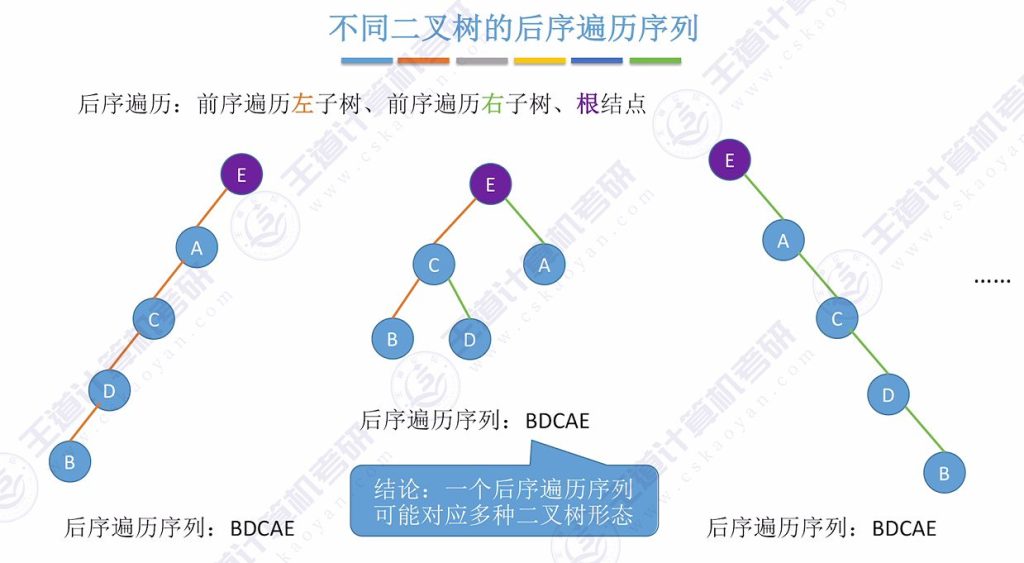
4)求后序遍历序列(后根遍历)
- 规则:左右根(LRN)
- 别名:后根遍历
- 递归过程:
- 递归后序遍历左子树
- 递归后序遍历右子树
- 访问根节点
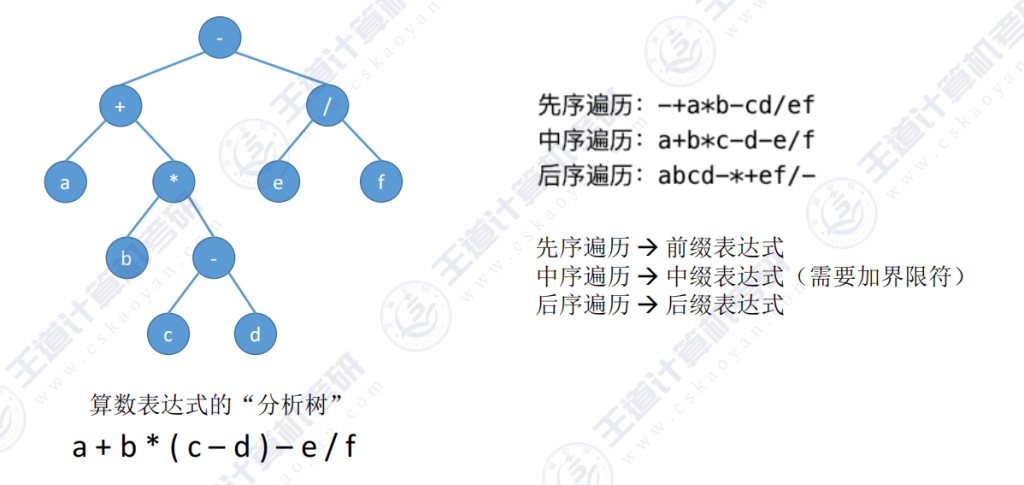
5.3 二叉树遍历的案例
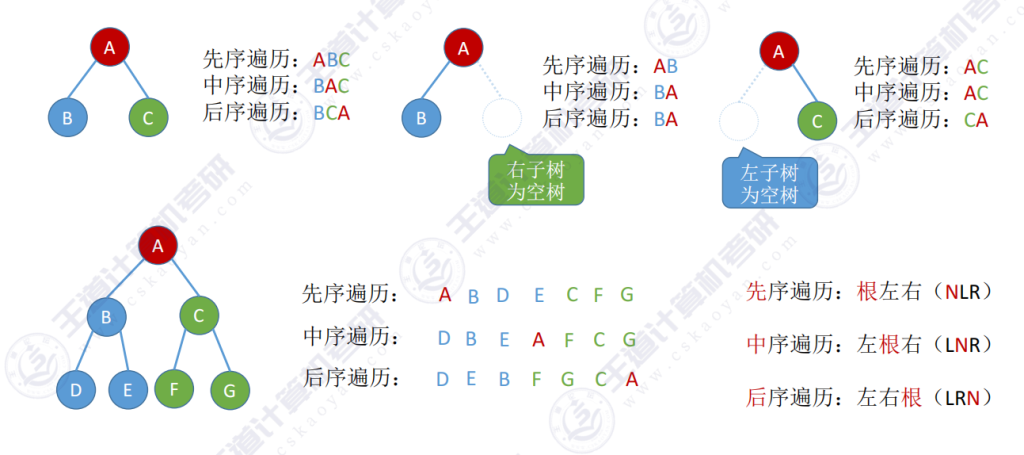
对于上图二叉树的先序遍历 AB,此时递归遍历 DE,后再到C,再递归FG
对于中序遍历,左根右,即 DBE A FCG
对于后序遍历,左右根,即 DEB FGC A
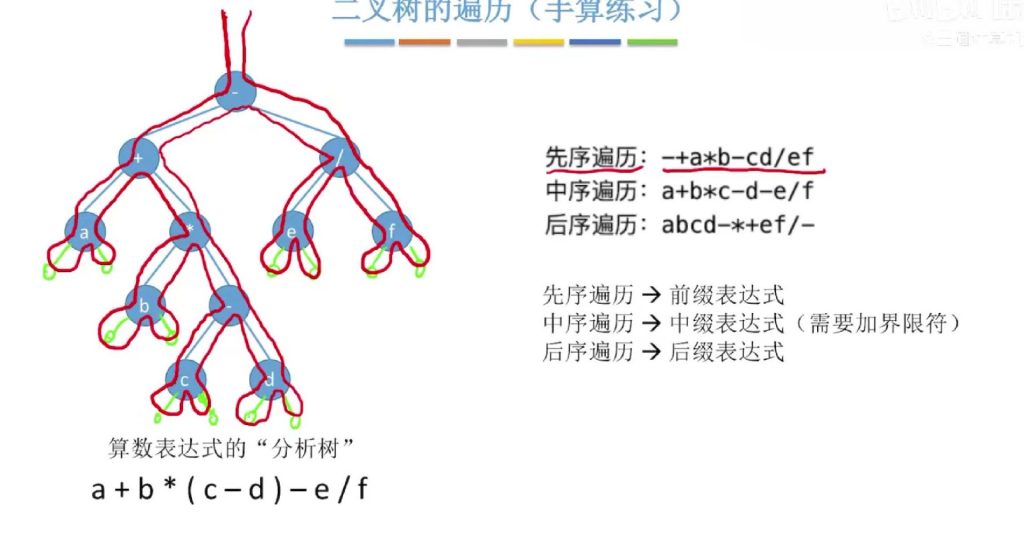
5.4 二叉树遍历 – 分支结点逐层展开法(手算练习)
案例一


案例二(真题类型)
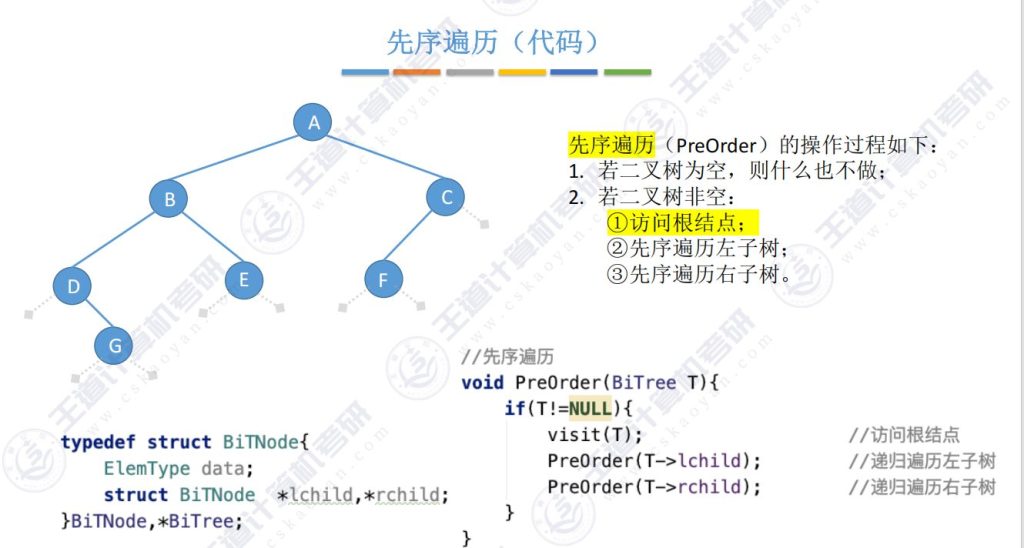
5.5 二叉树遍历(代码)- 先序遍历
王道视频二叉树的先序遍历递归的刨析:13分左右
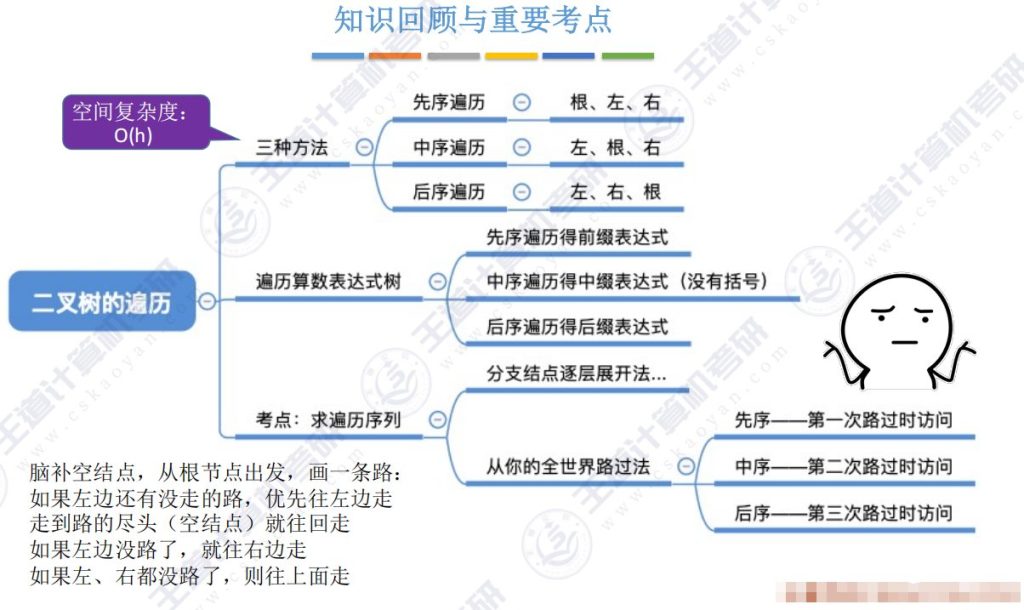
空间复杂度O(h)
每一个结点会被路过3次,第一次路过时访问结点
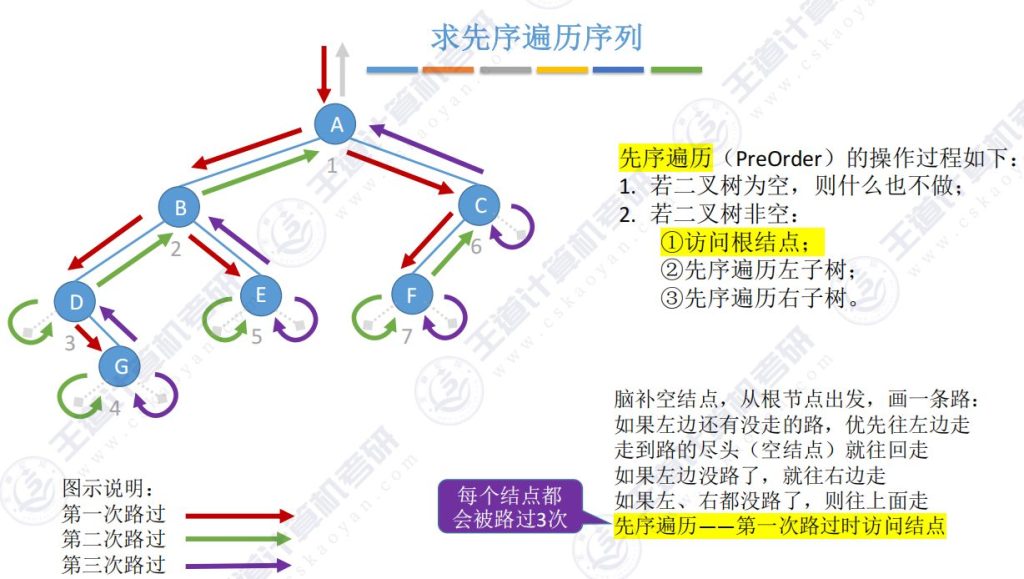
5.6 二叉树遍历(代码)- 中序遍历
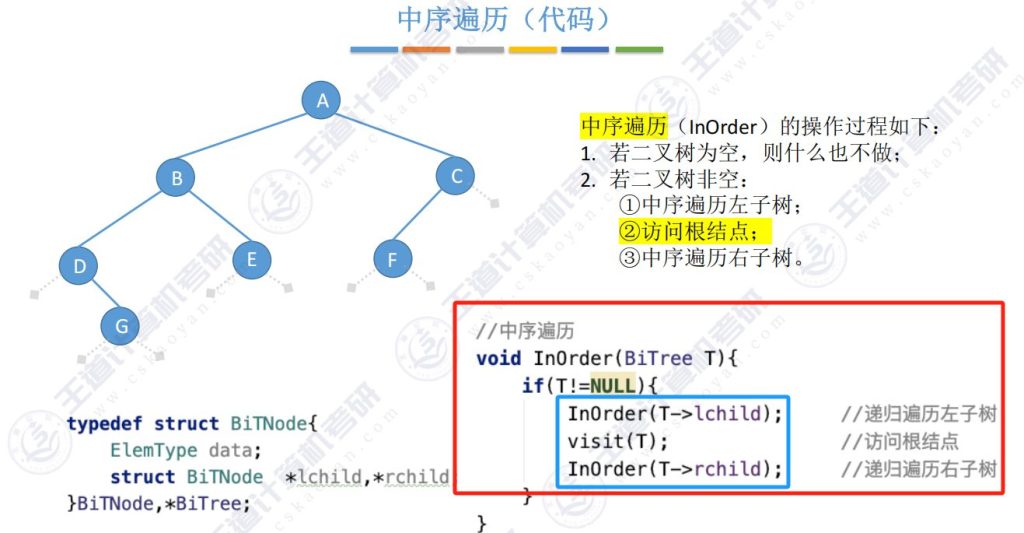
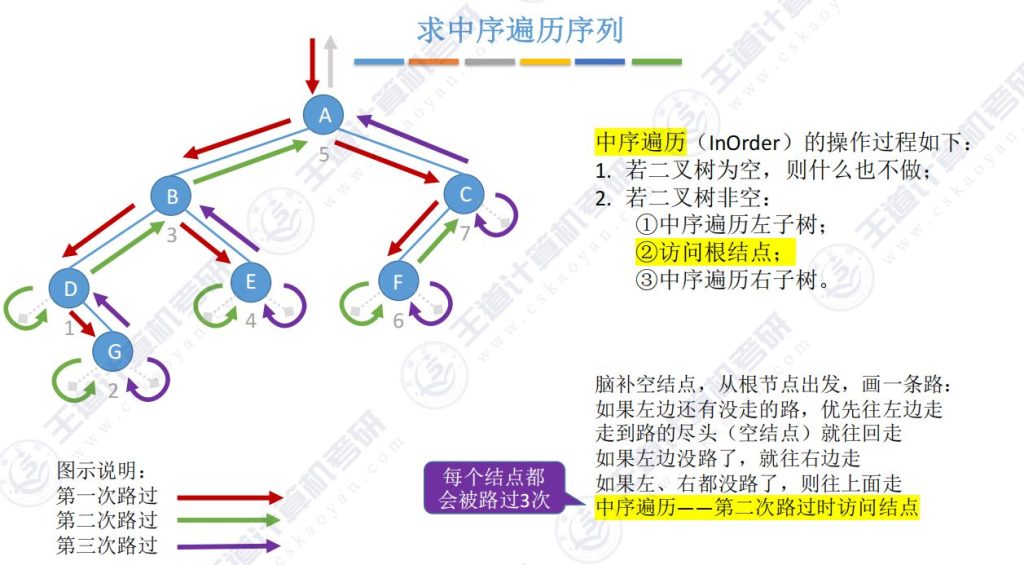
每个结点都被路过3次,第二次路过结点时访问结点
5.7 二叉树遍历(代码)- 后序遍历
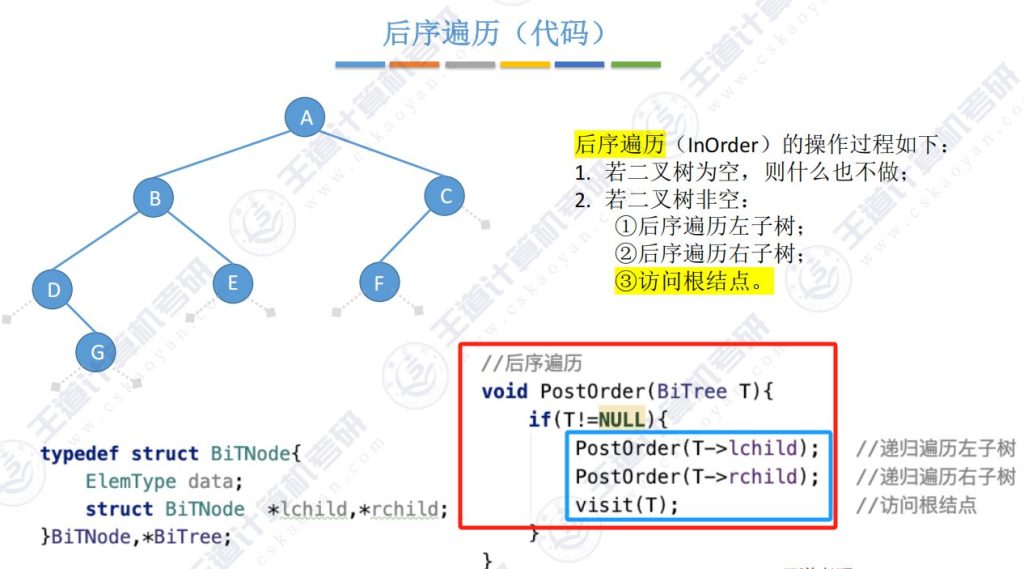
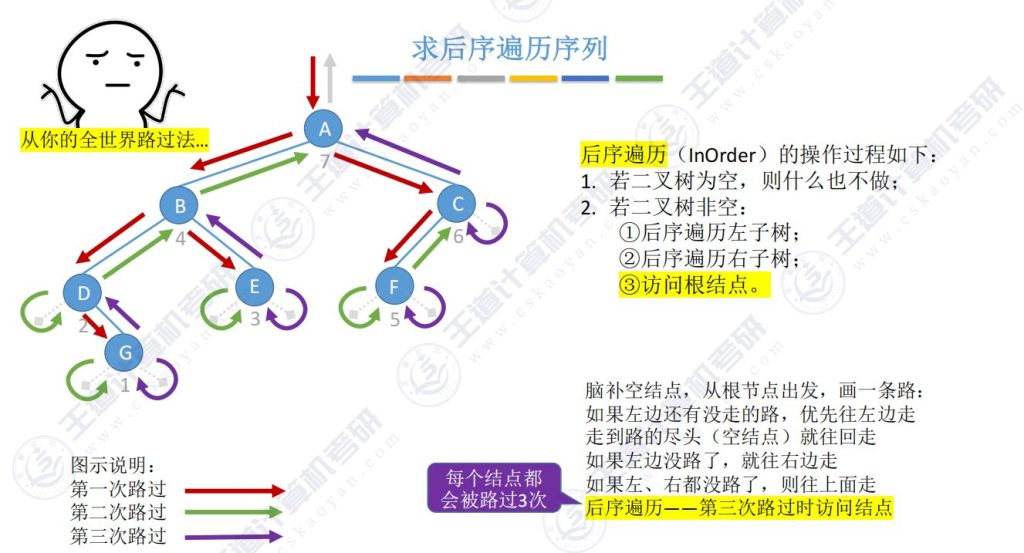
每个结点都被路过3次,第三次路过结点时访问结点
5.8 练习
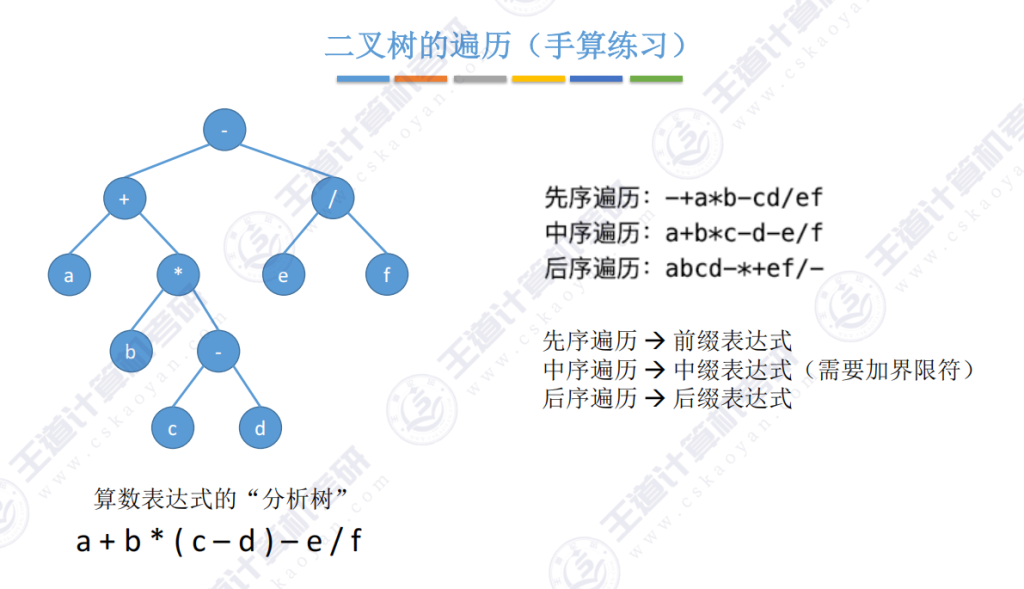
5.9求树的深度(应用)

- 递归思路:
- 若树为空,返回深度0
- 递归计算左子树深度 l 和右子树深度 r
- 取max(l,r)+1作为当前树深度
- 本质:该算法是后序遍历的变种,遵循”左右根”的处理顺序
5.10 知识回顾
重点掌握一种遍历算法
六、二叉树的层序遍历
6.1 层序遍历算法思想
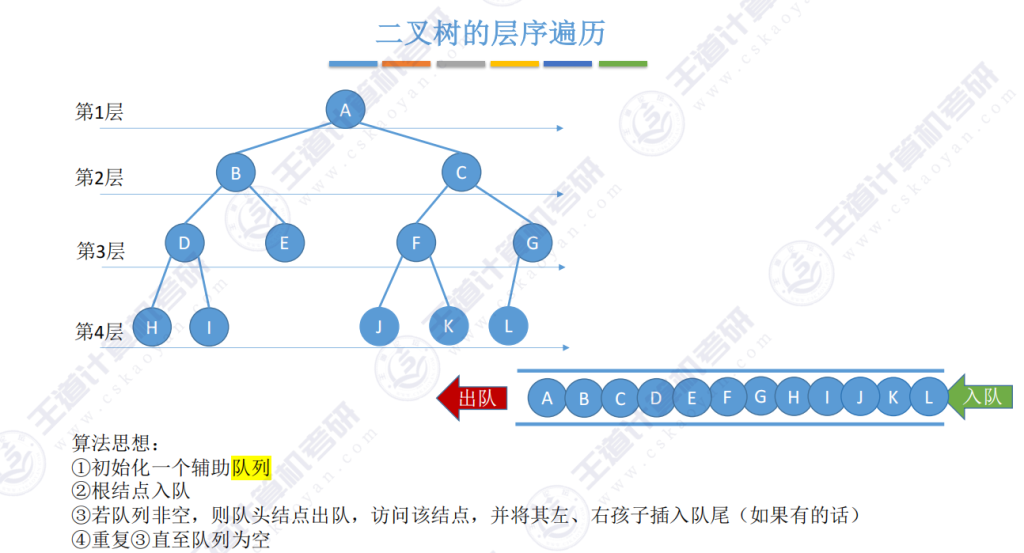
- 遍历顺序:按照从上到下、从左到右的顺序逐层访问节点,示例二叉树的遍历序列为abcdefghijkl
- 核心数据结构:需要使用辅助队列实现
- 算法步骤:
- 初始化:创建一个空队列
- 根节点入队:将二叉树的根节点放入队列
- 循环处理:
- 队头节点出队并访问
- 将该节点的左孩子(若存在)入队
- 将该节点的右孩子(若存在)入队
- 终止条件:队列为空时遍历结束
- 处理细节:叶子节点(如e节点)没有左右孩子,访问后不会有新节点入队
6.2 层序遍历代码实现

- 数据结构定义:
- 二叉树节点:
- 链队列节点:
- 队列结构:
- 实现要点:
- 空间优化:队列中存储节点指针而非节点本身,节省内存空间
- 核心逻辑:
- 设计选择:使用链队列而非顺序队列,便于动态扩展,适应不确定的节点数量
6.3 知识回顾

七、由遍历序列构造二叉树
7.1 不同二叉树的中序、前序、后续、层序遍历序列
中序遍历
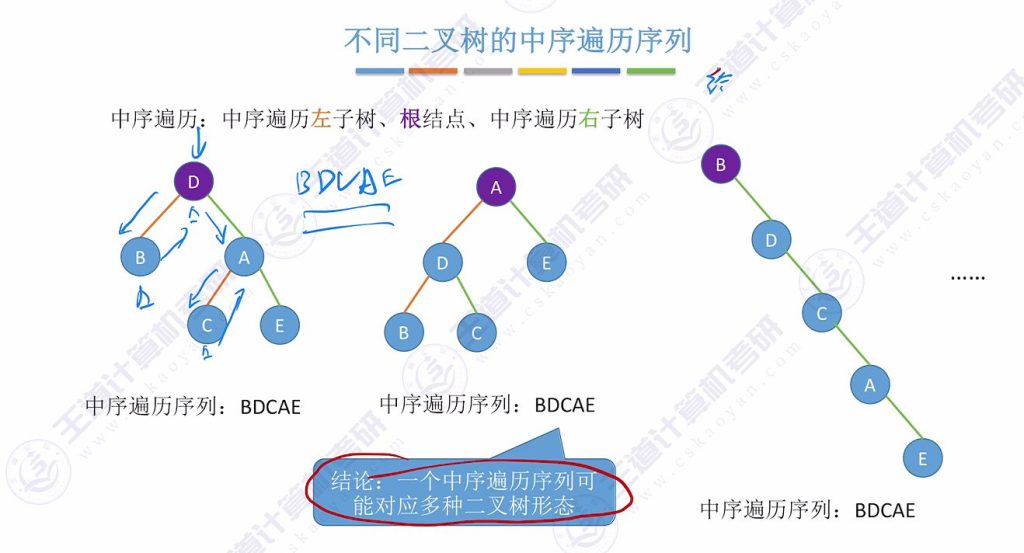
中序遍历
后续遍历
层序遍历
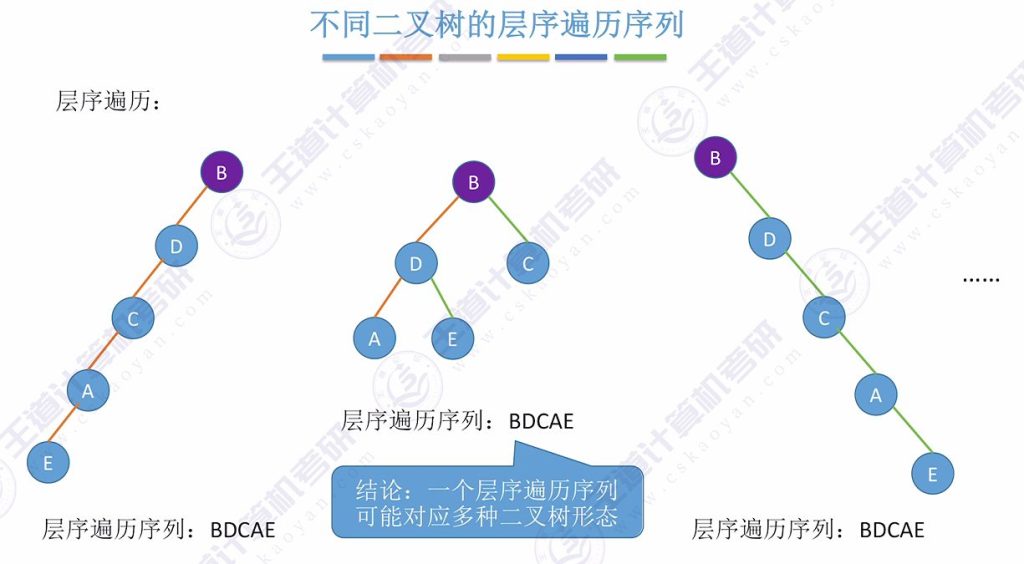
重要结论: 仅凭单一遍历序列(前/中/后/层序)无法唯一确定二叉树结构
7.2 由遍历序列构造二叉树
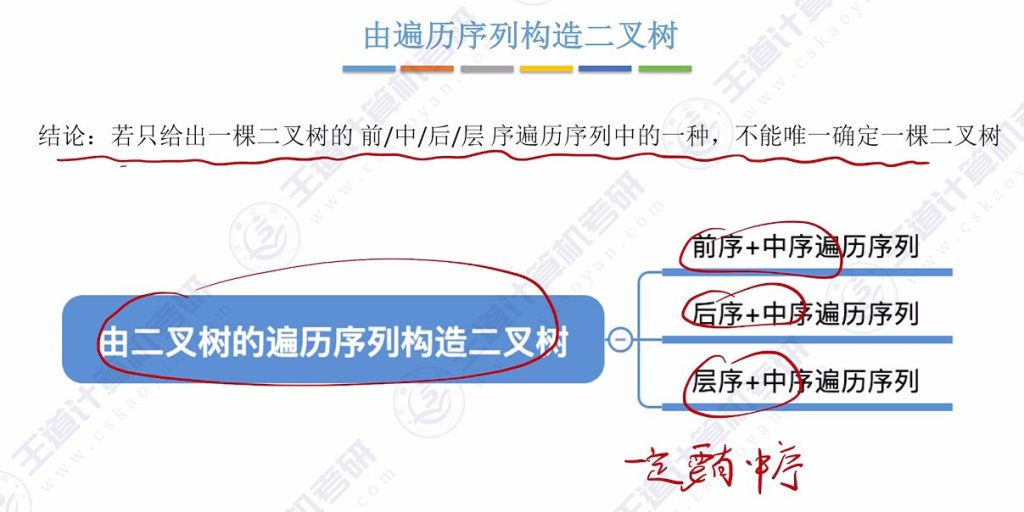
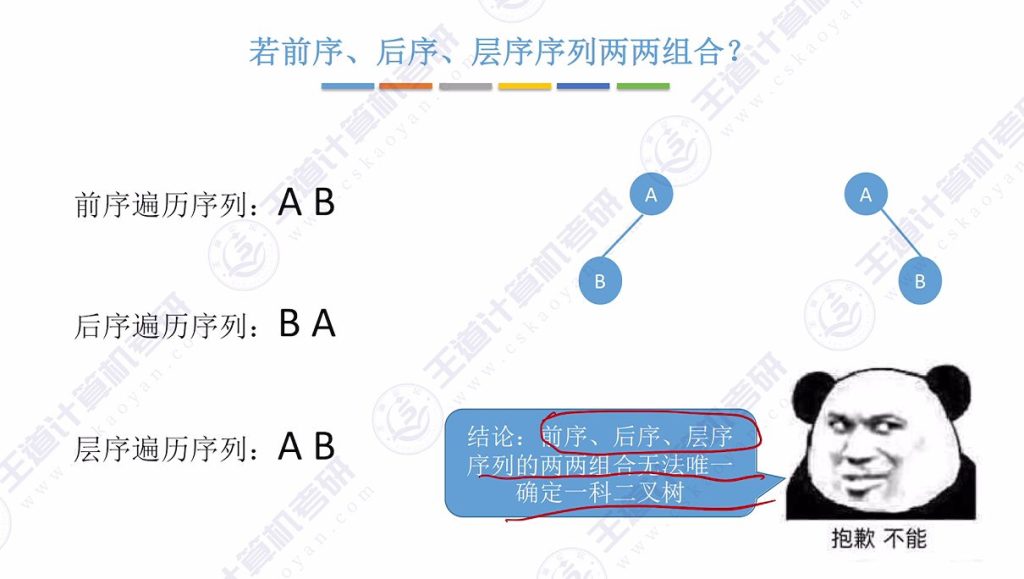
结论:若只给出一棵二叉树的前/中/后/层序遍历序列中的一种,不能唯一确定一棵二叉树
两两组合一定需要有中序遍历才能构造二叉树
7.3 前序+中序遍历序列
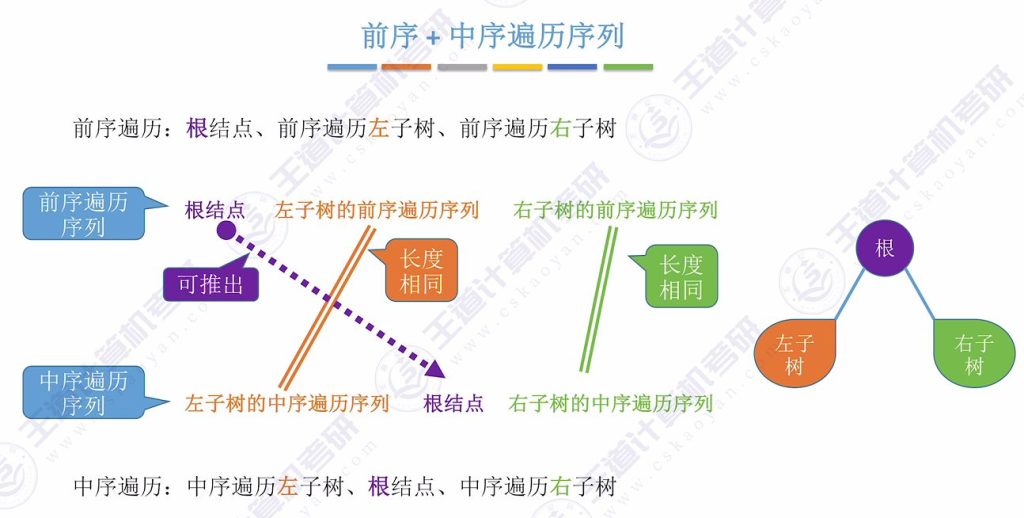
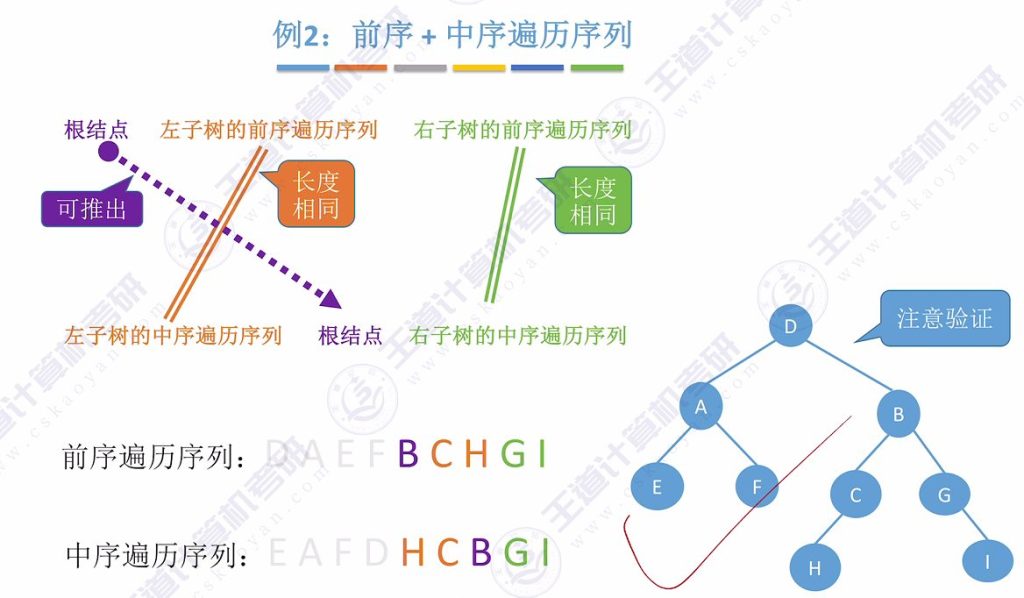
- 核心方法:
- 前序序列首元素为根结点
- 在中序序列中定位根结点,划分左右子树
- 递归处理左右子树
- 关键步骤:
- 根据前序确定根节点
- 根据中序确定左右子树范围
- 通过子树长度验证序列对应关系
例题1:前序+中序遍历序列
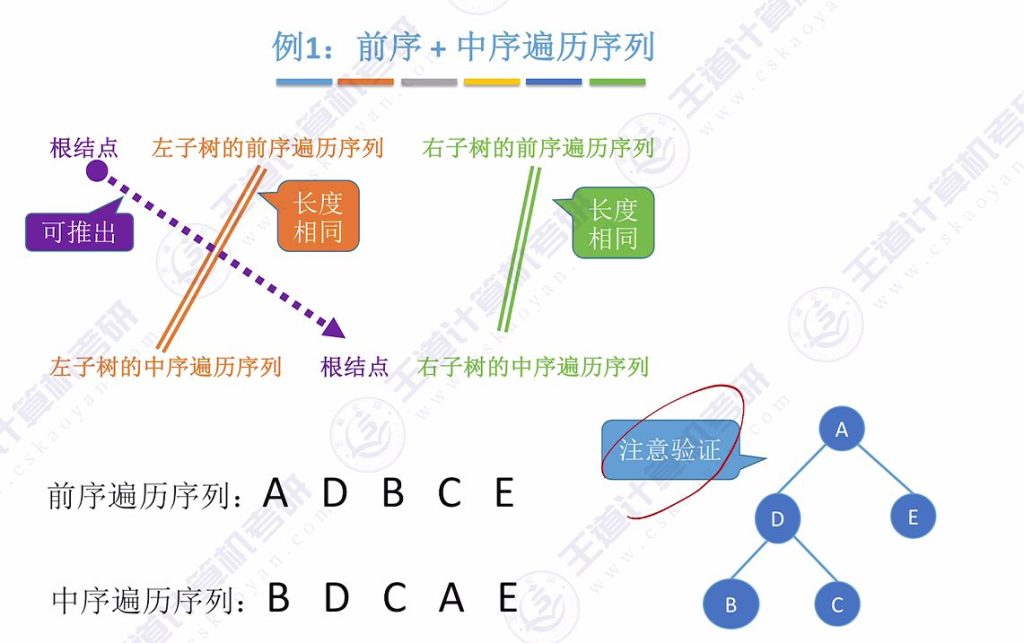
例题2:前序+中序遍历序列
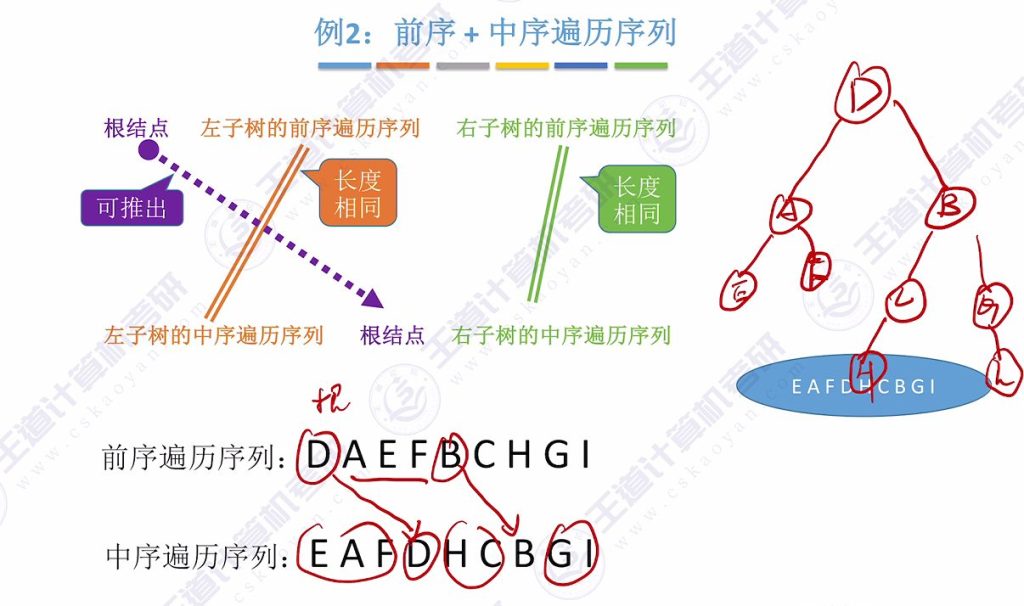
7.4 后续+中序遍历序列
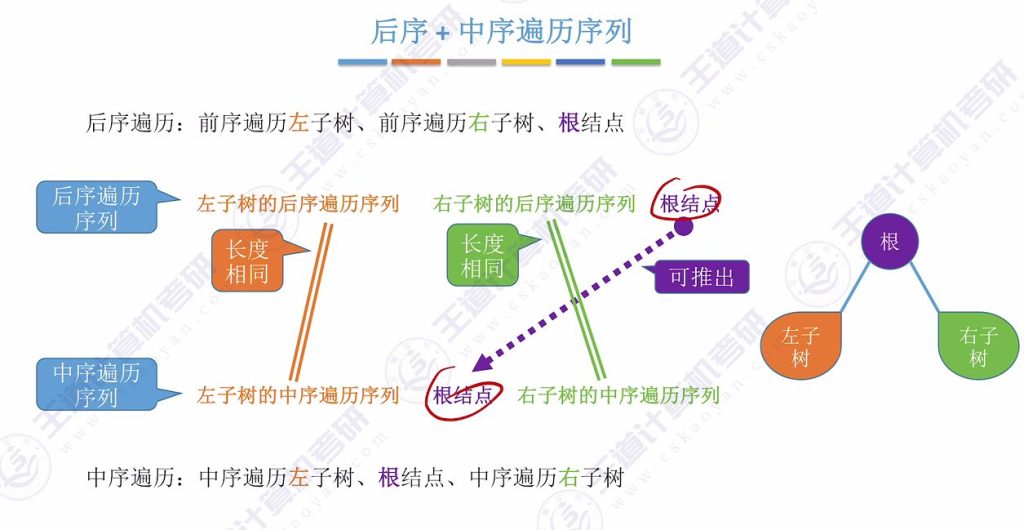
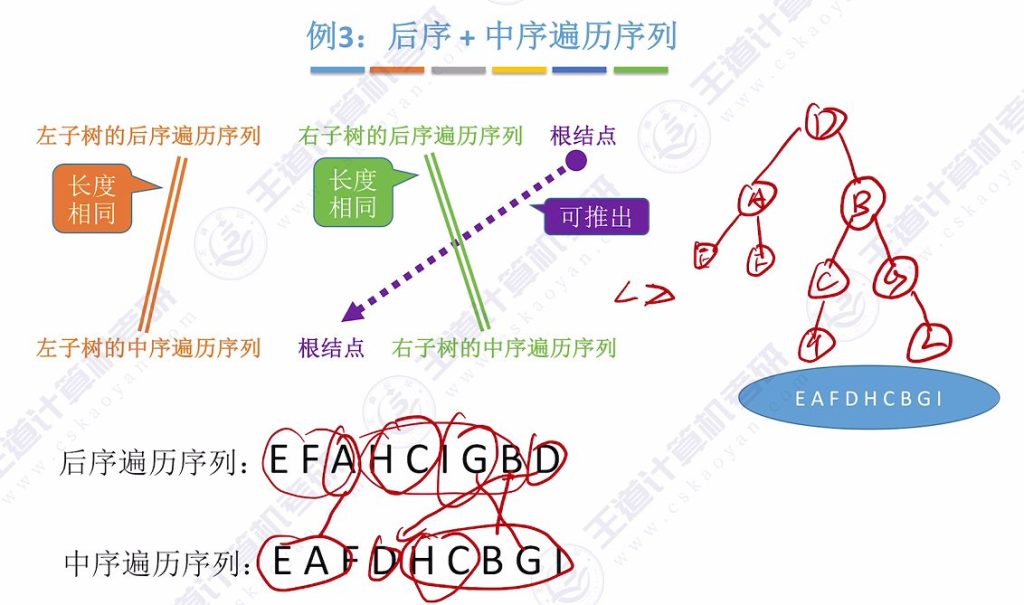
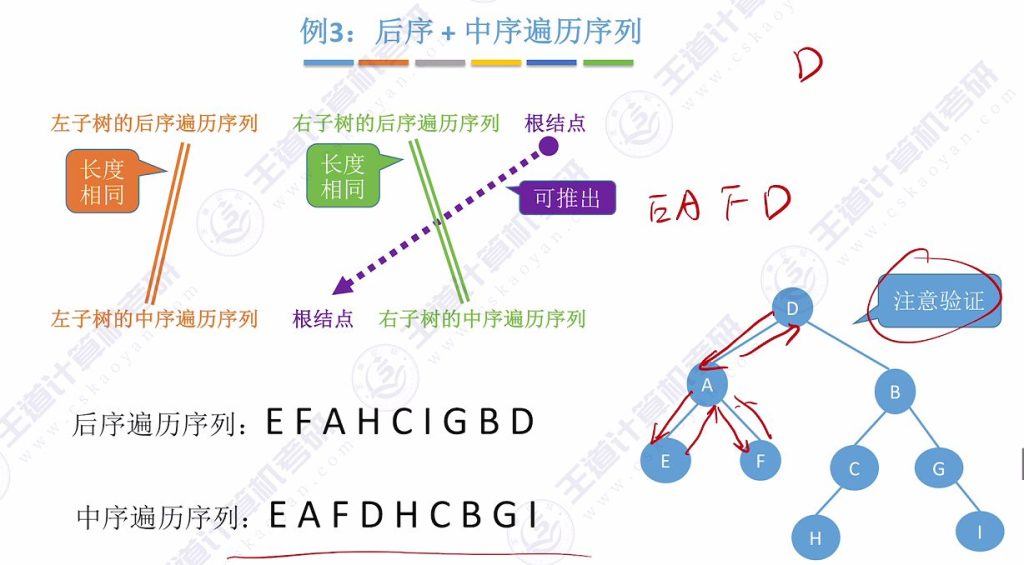
- 核心方法:
- 后序序列末元素为根结点
- 在中序序列中定位根结点位置
- 递归处理左右子树
例题3:后序+中序遍历序列
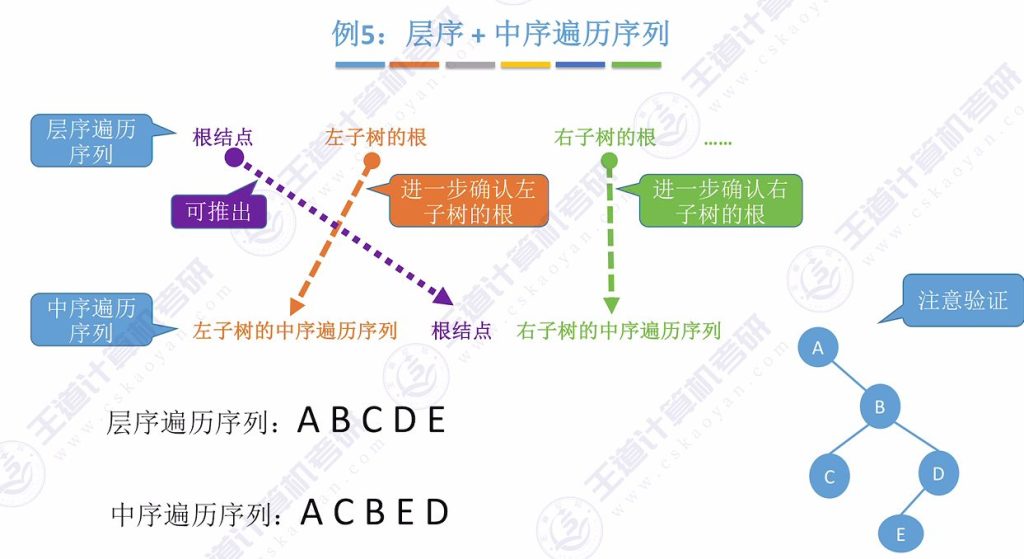
7.5 层序+中序遍历序列
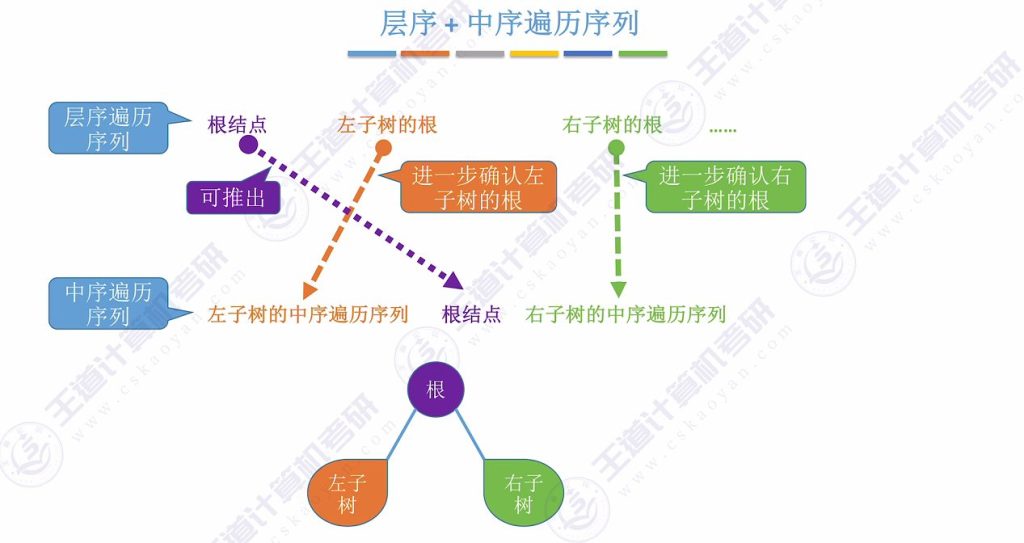
- 核心方法:
- 层序序列首元素为根结点
- 后续元素为左右子树的根
- 结合中序序列确定子树划分
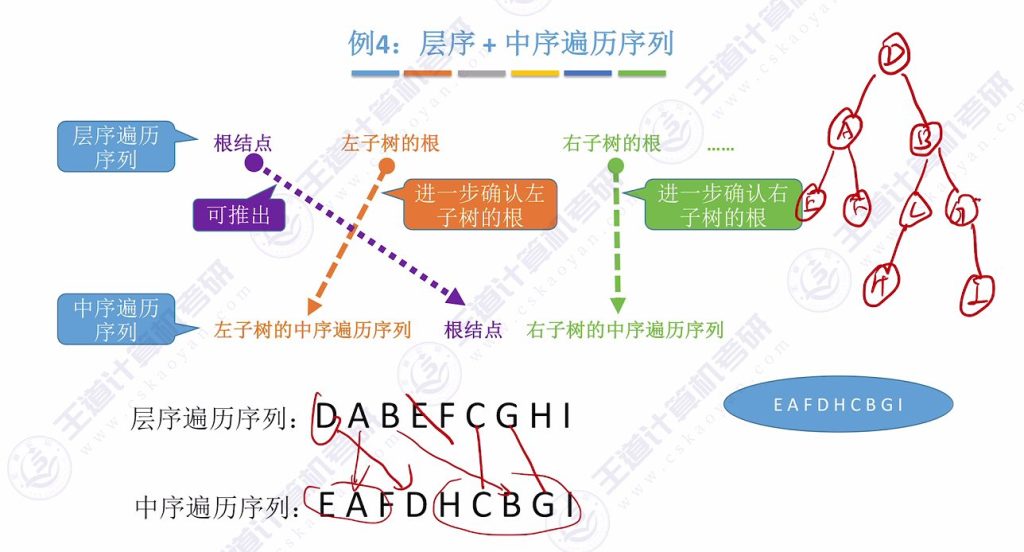
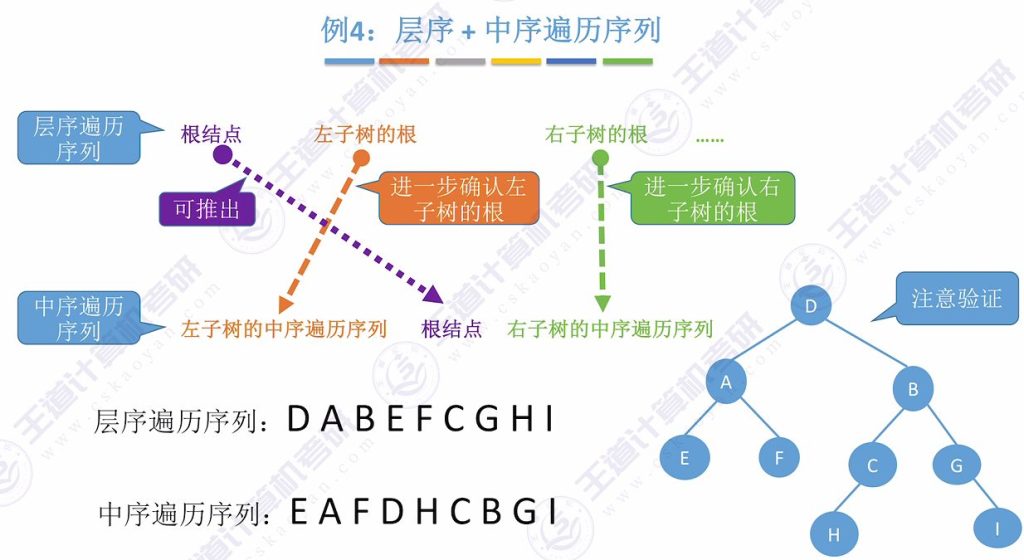
例题4:层序+中序遍历序列
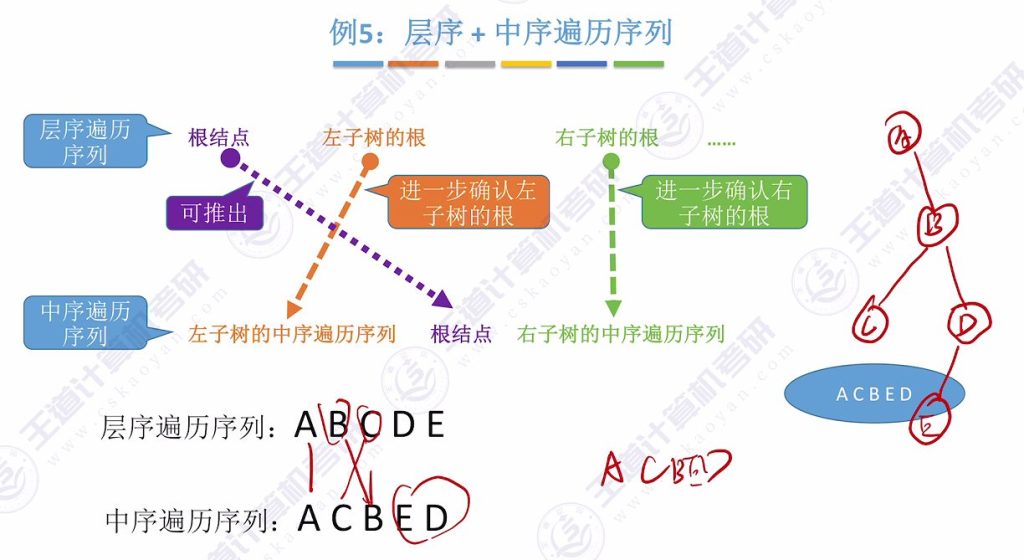
例题5:层序+中序遍历序列
7.6 知识回顾与重要考点
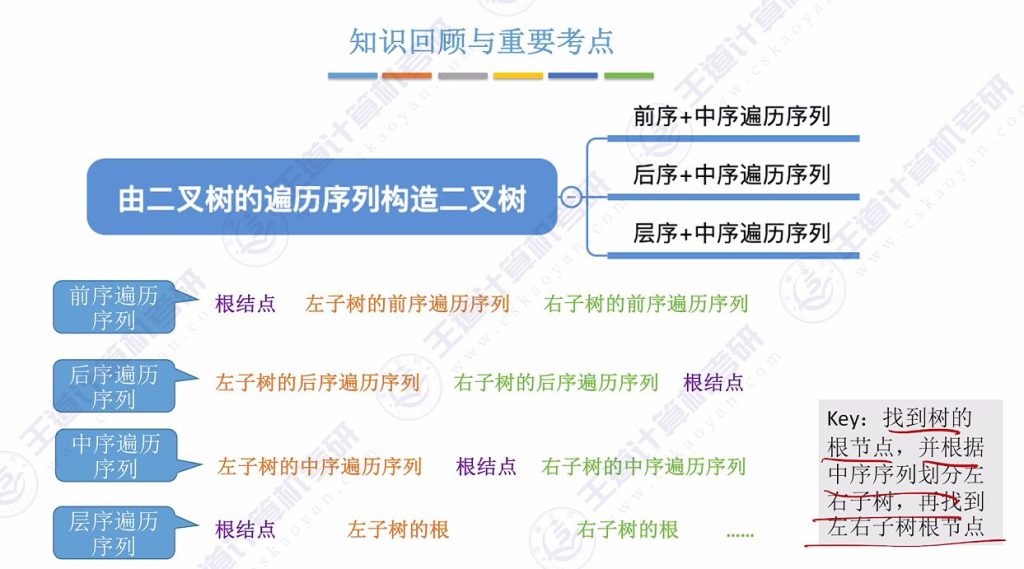
- 核心要点:
- 必须包含中序遍历序列才能唯一确定二叉树
- 前序/后序/层序两两组合无法唯一确定树结构
- 解题步骤:
- 通过非中序序列确定根节点
- 利用中序序列划分左右子树
- 递归处理各子树
- 特殊说明:
- 前序+后序组合示例:AB和BA可对应两种不同树形
- 层序+前序组合同样存在歧义
- 记忆口诀: “无中序不唯一,有中序可递归”
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客