一、知识总览
1.哈夫曼树是二叉树的一种,主要用于数据压缩和编码。
2.构造哈夫曼树的关键是选择权值最小的节点进行合并。
3.哈夫曼树的应用包括哈夫曼编码,用于优化数据传输的效率。
二、带权路径长度
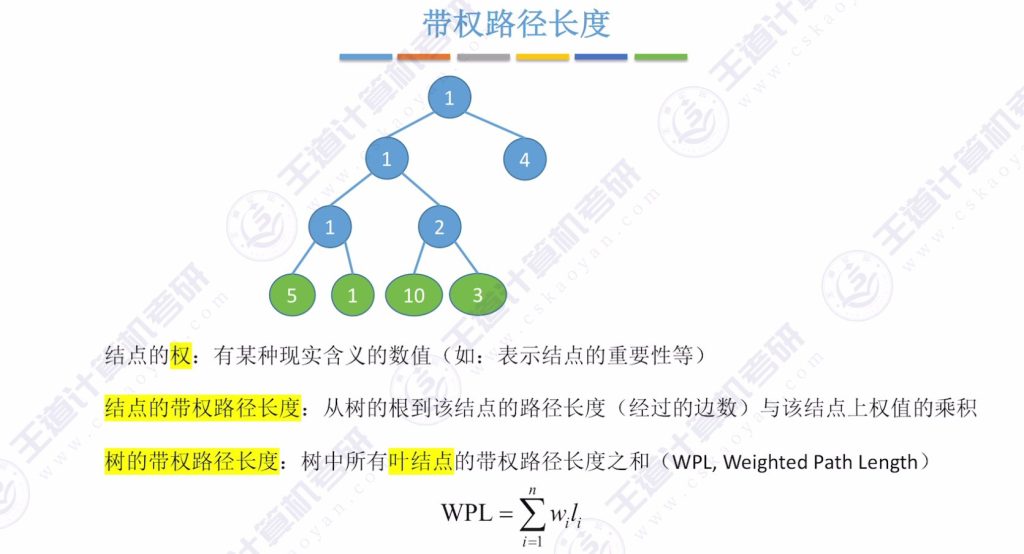
三、哈夫曼树的定义
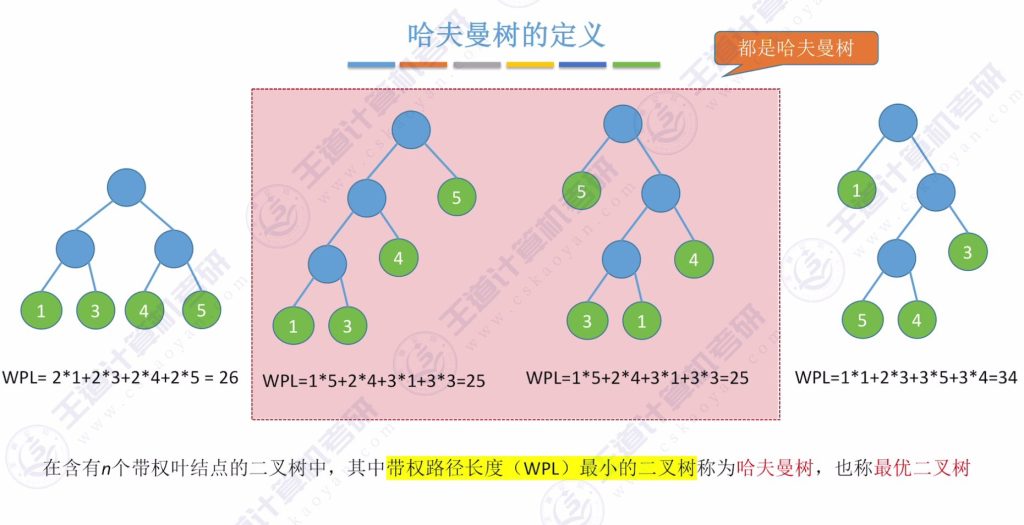
- 哈夫曼树定义:带权路径长度最小的二叉树
- 别名:最优二叉树
- 构造条件:给定n个带权叶子节点
- 比较范围:所有含这n个叶子节点的二叉树
- 核心特征:最小化带权路径长度
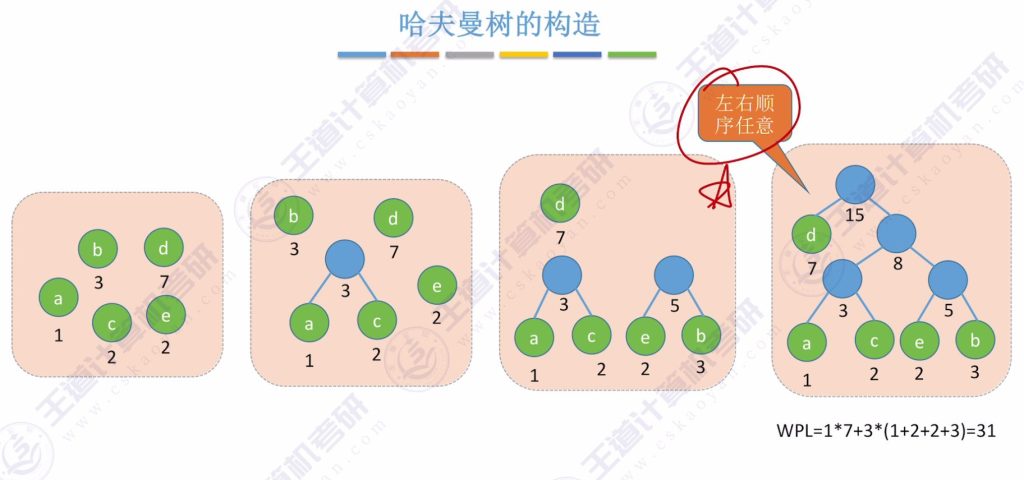
四、哈夫曼树的构造
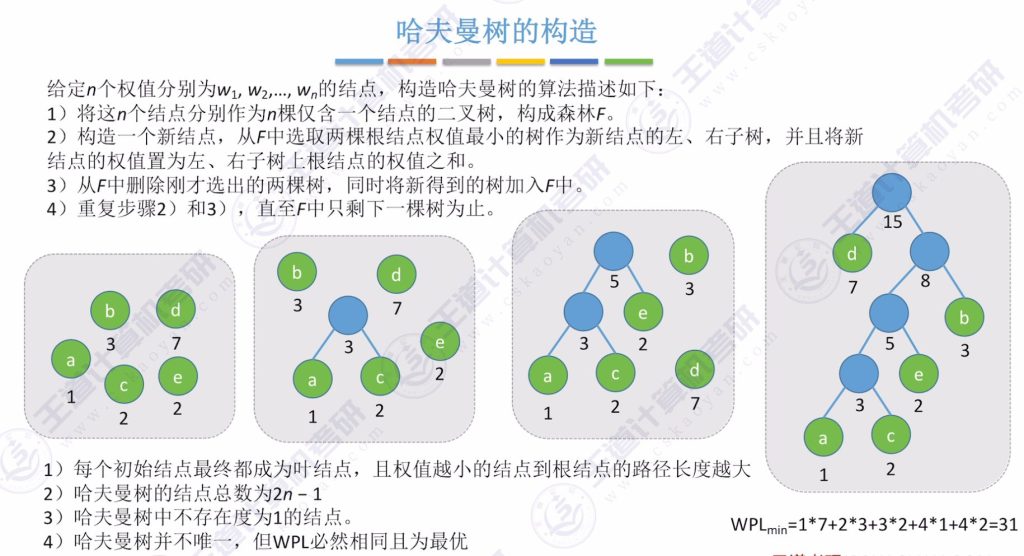
- 哈夫曼树构造方法:每次选择两个权值最小的节点结合成兄弟节点。
- 新树权值计算:新生成的树的根节点权值为两个子节点权值之和。
- 带权路径长度(WPL):哈夫曼树的WPL是所有叶子节点的权值乘以其到根节点路径长度之和。
- 构造步骤:重复选择最小权值节点结合,直到只剩一棵树。
- 最优性:哈夫曼树的WPL是所有可能树中最小的。
- 节点选择:构造过程中可选择任意两个最小权值节点,顺序不影响最终结果。
五、哈夫曼编码
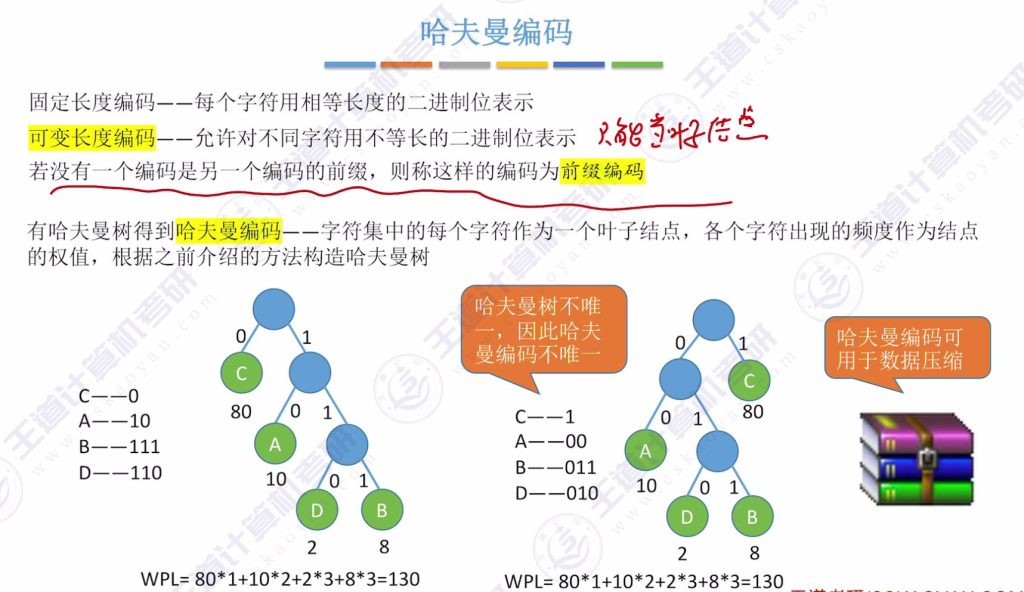
1.哈夫曼编码基于哈夫曼树的原理,用于优化数据传输的效率。 2.哈夫曼编码采用可变长度编码,根据字符出现的频率分配不同的二进制码长。 3.前缀编码:任何字符的编码都不是另一个编码的前缀,避免解码歧义。 4.哈夫曼编码适用于英文等文本数据的压缩,可以显著减少数据传输量。
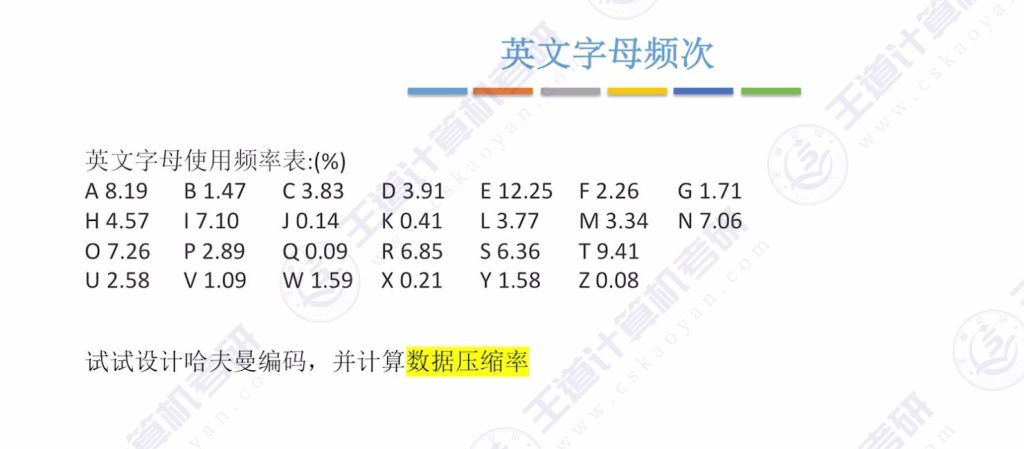
六、哈夫曼树的应用
七、知识回顾
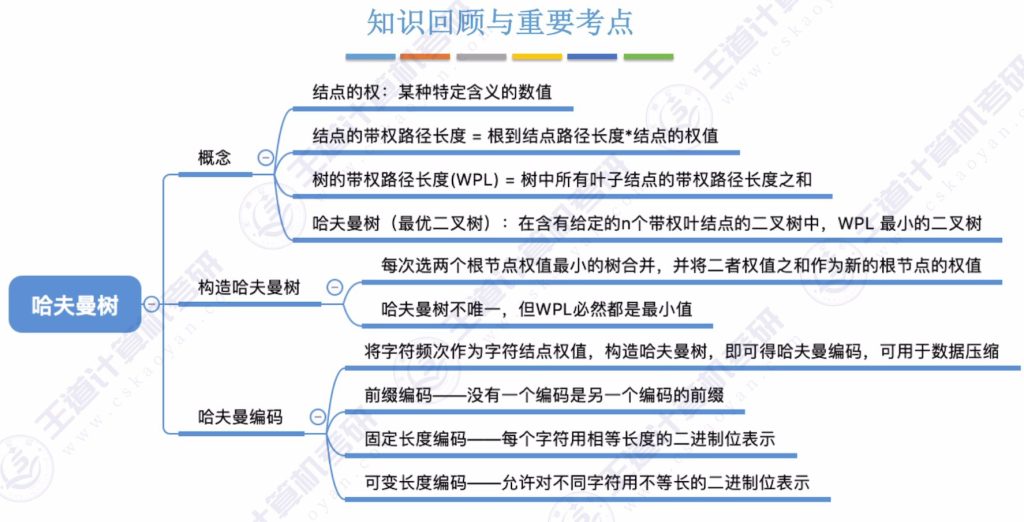
重要概念:
- 节点权值
为树中每个节点附上一个数值,称为权值,表示节点的某种现实含义,如重要性等。 - 节点的带权路径长度
从根节点到指定节点的路径长度(经过的边数)与该节点权值的乘积。
例如:某节点权值为3,从根节点到该节点的路径长度为3,则其带权路径长度为 3 × 3 = 9。 - 树的带权路径长度(WPL)
树的带权路径长度是所有叶子节点的带权路径长度之和,记为 WPL。
示例:- 树1:4个叶子节点,路径长度均为2,权值分别为a、b、c、d,WPL = 2a + 2b + 2c + 2d。
- 树2:叶子节点权值为5(路径长度1)、4(路径长度2)、1和3(路径长度3),WPL = 1×5 + 2×4 + 3×1 + 3×3 = 25。
哈夫曼树的定义:
哈夫曼树(最优二叉树):给定n个带权叶子节点,在所有包含这n个叶子节点的二叉树中,WPL最小的二叉树。
示例:对于权值为1、3、4、5的4个叶子节点,WPL最小值为25的树即为哈夫曼树,可能有多种形态。
哈夫曼树的构造:
构造步骤:
- 从节点集合中选择权值最小的两个节点,将其作为兄弟节点,生成新树,新树的根节点权值为两者之和。
- 将新树加入集合,移除原两个节点。
- 重复上述步骤,直到集合中只剩一棵树。
示例:权值为1、2、3、7的节点:
初始集合:{a:1, b:2, c:3, d:7}
1. 选择a(1)和c(3),生成新树,根权值为1+3=4,集合更新为{b:2, e:4, d:7}
2. 选择b(2)和e(4),生成新树,根权值为2+4=6,集合更新为{f:6, d:7}
3. 选择f(6)和d(7),生成最终树,根权值为6+7=13最终WPL为31,验证为最小值。
哈夫曼树的性质:
- 初始节点均为叶子节点,权值越小的节点路径长度越长。
- n个节点需合并n-1次,总节点数为2n-1。
- 不存在度为1的节点。
- 哈夫曼树不唯一,但WPL相同且最优。
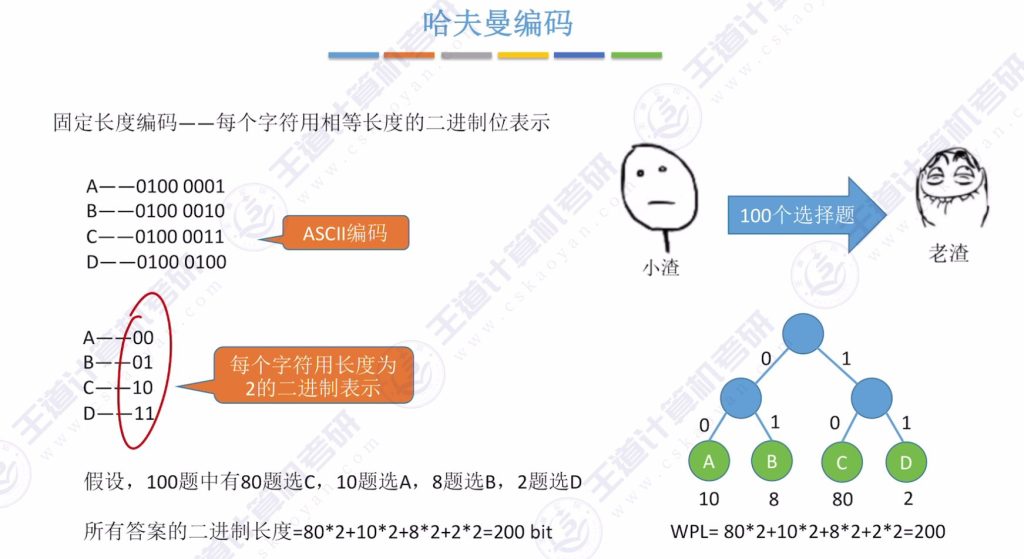
哈夫曼编码:
应用场景: 数据压缩,如电报传输(点.和划-对应二进制0和1)。
构造方法:
- 将字符集中的字符作为叶子节点,字符出现频率作为权值,构造哈夫曼树。
- 从根节点出发,左路径为0,右路径为1,生成各字符的编码。
示例:字符集{a:10, b:8, c:80, d:2}(100个选择题答案,c占80次):
1. 选择d(2)和b(8),生成新树,根权值为10
2. 选择新树(10)和a(10),生成新树,根权值为20
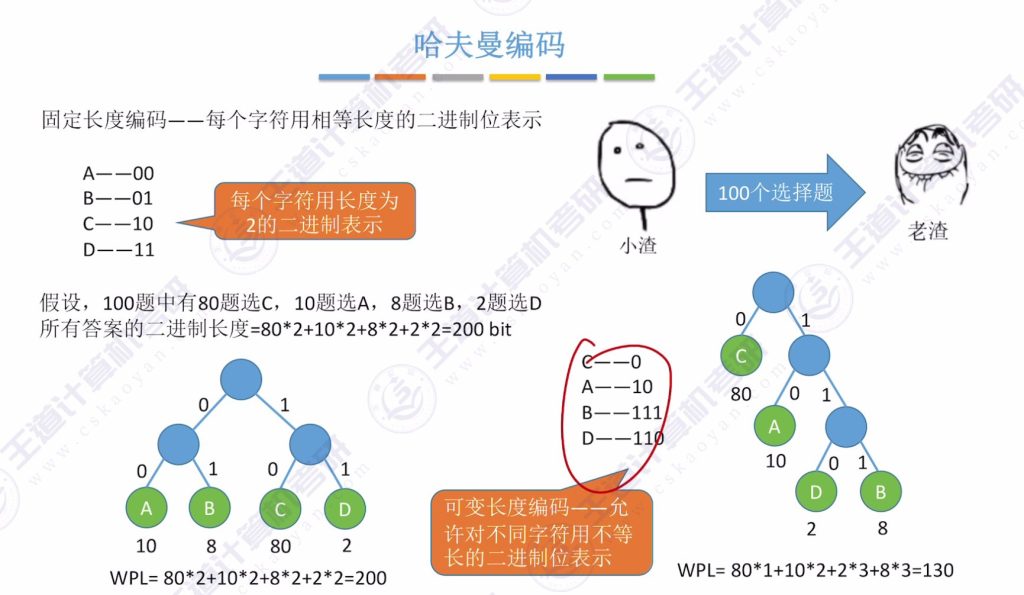
3. 选择新树(20)和c(80),生成最终树编码结果:
c: 0 (80次,80×1)
a: 10 (10次,10×2)
b: 110 (8次,8×3)
d: 111 (2次,2×3)
WPL = 80×1 + 10×2 + 8×3 + 2×3 = 130总传输比特数为130,远少于固定长度编码(如ASCII的800比特)。
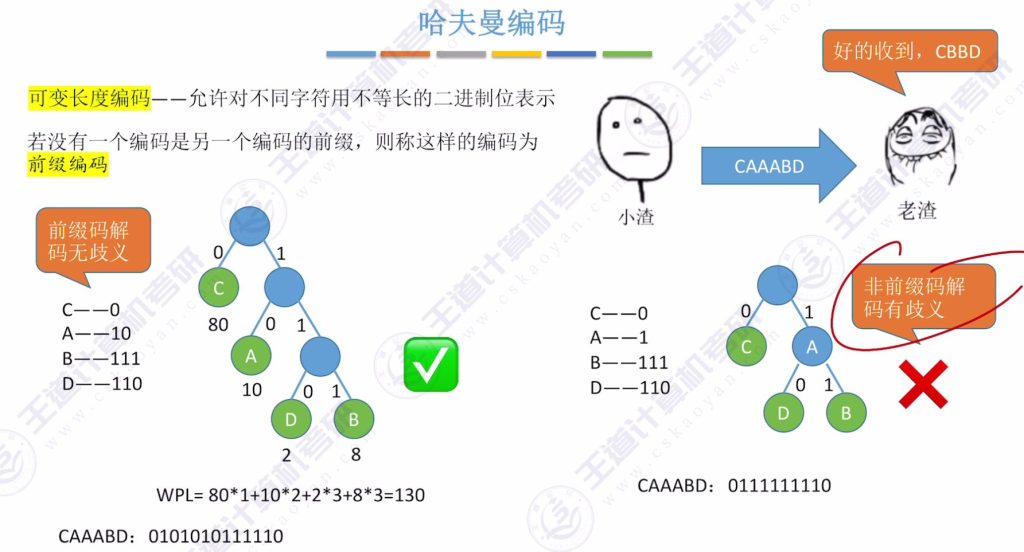
前缀编码:
哈夫曼编码是前缀编码,即任一字符的编码不是另一字符编码的前缀,避免解码歧义。
反例:若a编码为1,b为111,解码“111”可能误为“a”或“b”,导致错误。
特点:
- 可变长度编码:频率高的字符编码短,频率低的编码长。
- 不唯一:不同哈夫曼树生成不同编码,但总比特数(WPL)相同。
- 应用:数据压缩,如英文26字母按频率编码可显著减少数据量。
总结:
- 核心概念:树的带权路径长度(WPL)。
- 哈夫曼树:包含n个带权叶子节点且WPL最小的二叉树。
- 构造方法:每次合并权值最小的两棵树,合并n-1次。
- 应用:哈夫曼编码,用于数据压缩,确保前缀编码无歧义。
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


