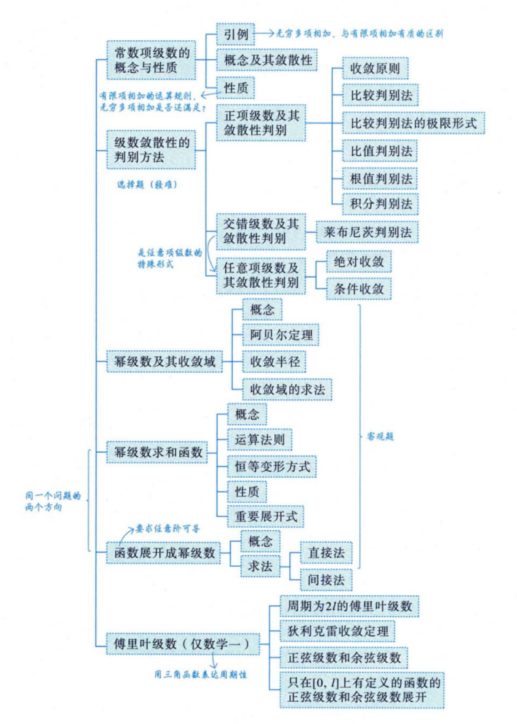
级数敛散性的判别方法
一、正项级数及其敛散性的判别
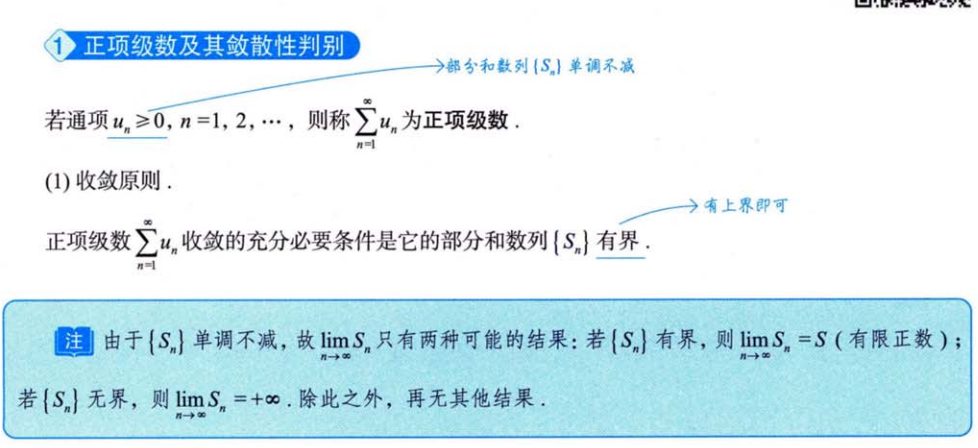
1、收敛原则
1.1、例题1敛散性的判别


解析


2、比较判别法

两个正项级数:大的收敛,小的必收敛;若小的发散,则大的必发散
2.1例题比较判别法

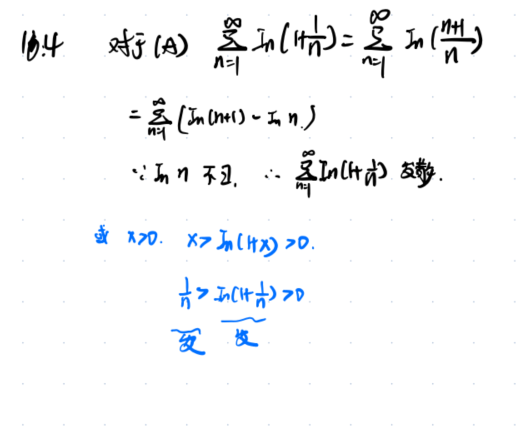
解析





具体函数比较判别法:跟上述两个比较
抽象问题得用不等式
2.2例题2 – 重要题源


解析



2.3例题3


解析


2.4例题4


解析



3、比较判别法的极限形式(无穷小比阶数)

0/0型,只有趋于0,才有意义
对于2 底下趋于 0 的速度快, 底下都发散了,上面肯定发散
3.1例题1
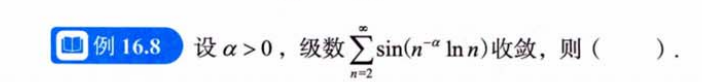
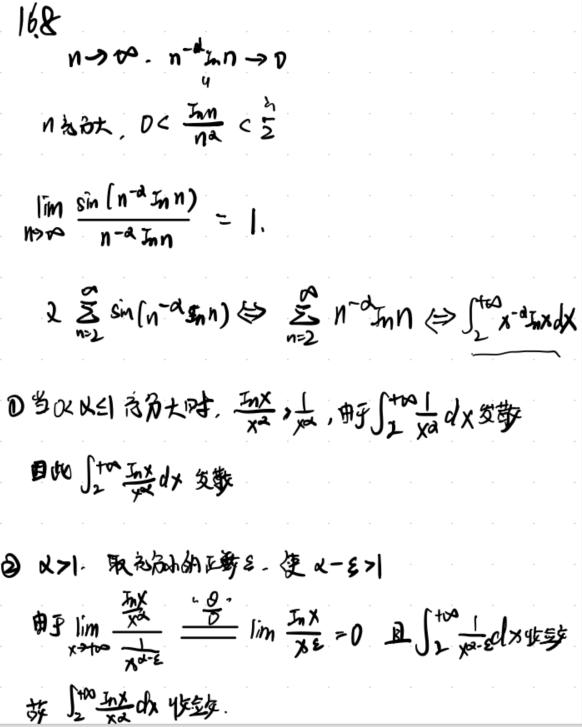
解析




3.2例题2
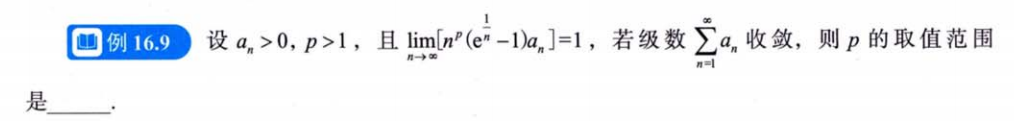
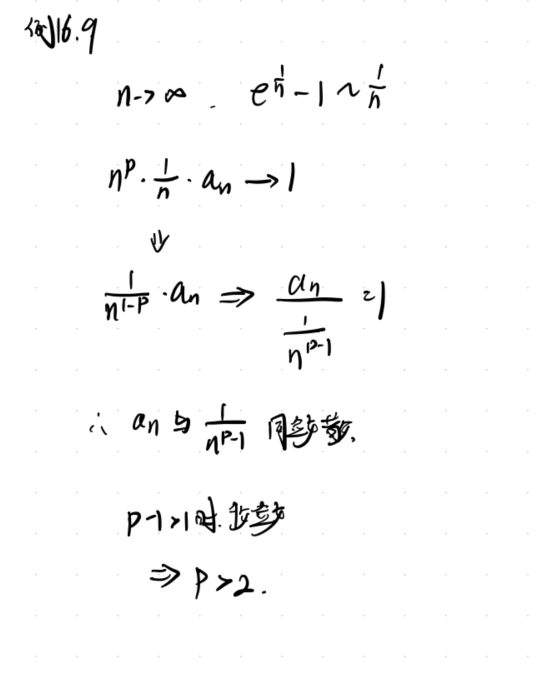
解析

3.3例题3
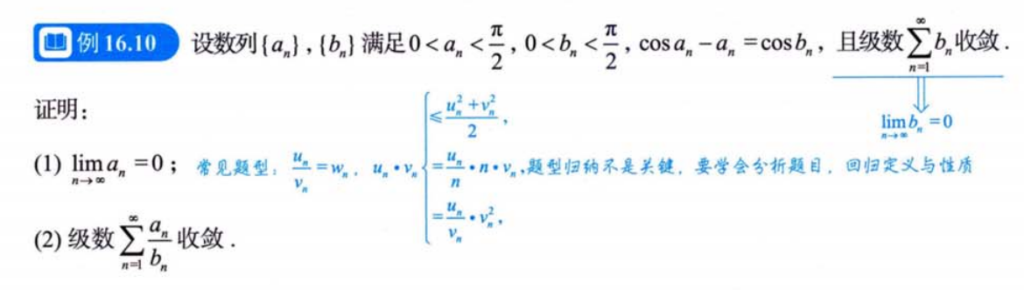

解析

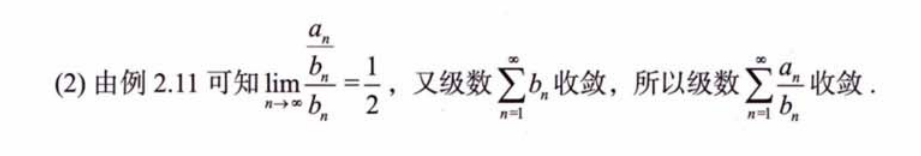
4、比值判别法


4.1例题1


解析

5、根值判别法


5.1例题1
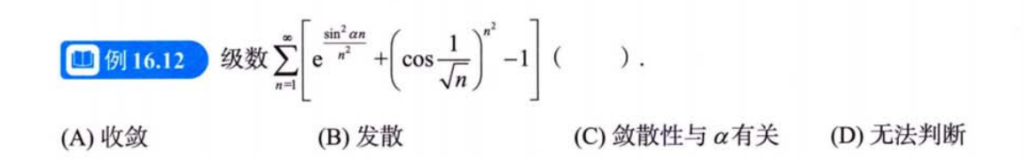

解析
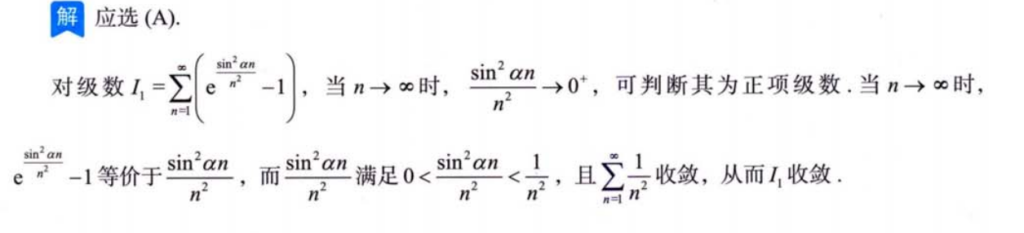

6、积分判别法

例题6.1


解析

二、交错级数敛散性判别
2.1 交错级数的定义

2.2 交错级数敛散性判定

2.3 交错级数 Un 单调性的判别
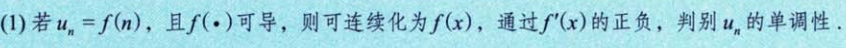

2.4 交错级数其他注明
莱布尼茨判别法只是判别交错级数的充分条件,判别交错级数敛散性的方法还有其他的,不是必要条件

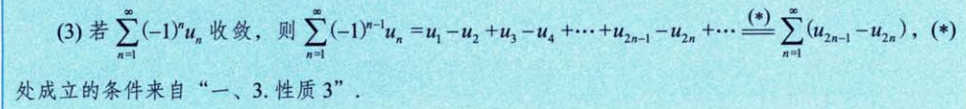
性质3,收敛级数的项任意加括号后所得的新级数仍然收敛,其和不变
2.5 例题1 – 判别交错级数敛散性问题

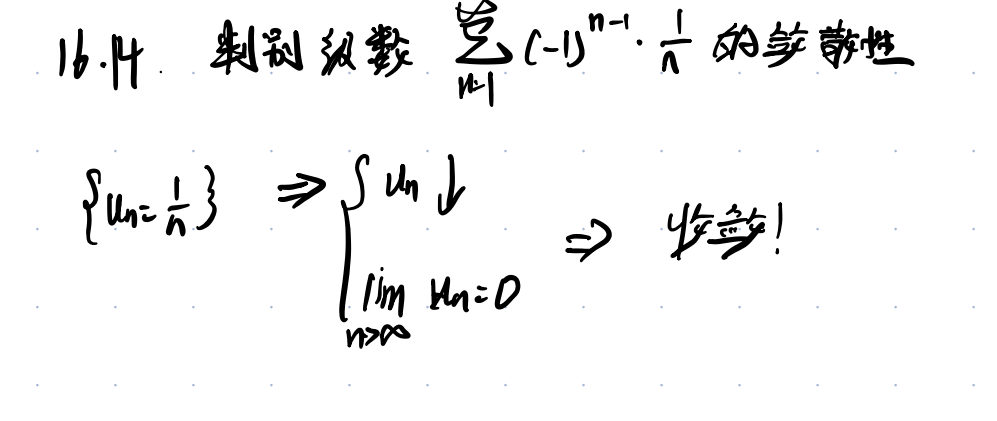
2.6 例题2 – 判别交错级数敛散性问题

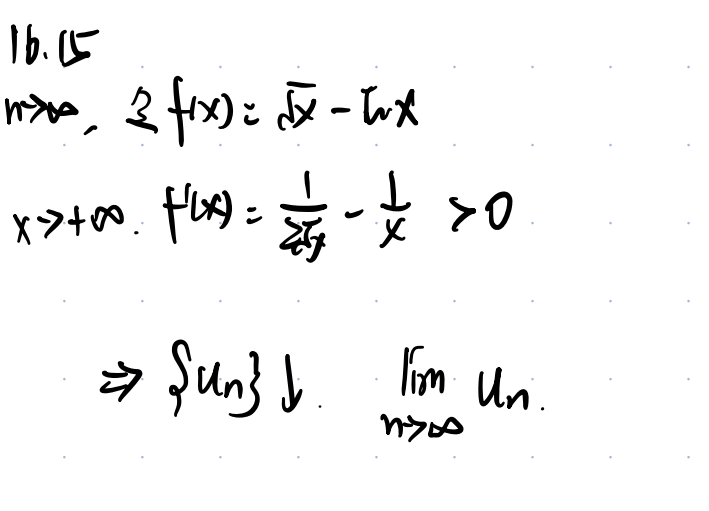

这里显然 根号x 的 速度 要远大于 Inx 的速度
2.7 例题3 – 判别交错级数敛散性问题



三、任意项级数及其敛散性判别(绝对值判别法)
3.1 任意项级数的定义

3.2 任意项级数的性质(绝对收敛、条件收敛)

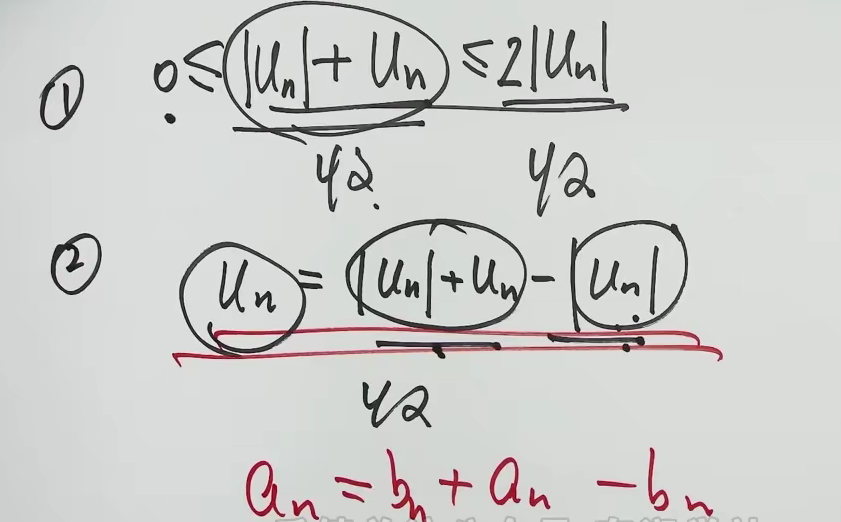
条件收敛:本身收敛,加绝对值发散
3.3 关于任意项级数的几点说明
说明1

说明2


说明3

说明4

说明5

说明6

说明7

3.4 例题1


3.5 例题2




3.6 例题3




3.6 例题3

四、抽象的数项级数的判别问题总结


前3个需要记忆,后面的需要判断
例题4.1


本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


