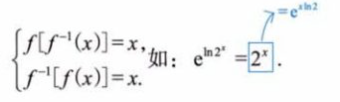一、基础知识结构
| 知识点 | 核心内容 | 考试重点/易混淆点 | 难度系数 |
| 函数的概念和特性 | 幂函数、指数函数、对数函数、三角函数、反三角函数等基本初等函数及其运算规则 | 函数概念和性质的深入理解对后续解题至关重要 | ★★★ |
| 函数图像 | 基本初等函数图像,分段函数图像 | 初等函数图像及其变换 | ★★ |
| 函数极限的概念 | 现代数学中极限概念的发展,经典与现代定义的结合 | 现代数学中极限概念的理解,与经典定义的互补 | ★★★★ |
| 函数极限的性质 | 极限的性质,无穷小与无穷大的概念 | 无穷小比阶的问题,极限性质的掌握 | ★★★ |
| 函数极限的计算 | 罗必达法则,泰勒公式,两个重要极限 | 罗必达法则与泰勒公式的应用,七种未定式的计算 | ★★★★★ |
| 函数的连续与间断 | 连续的概念,间断点的类型与判定 | 连续与间断的判定,间断点类型的识别 | ★★★ |
| 考试题型与重点 | 选择题、填空题、解答题 | 函数极限的概念与计算,连续与间断的判定 | ★★★★ |
| 重难点强调 | 洛必达法则,泰勒公式,极限概念的理解 | 极限概念的理解,洛必达法则与泰勒公式的熟练掌握 | ★★★★★ |
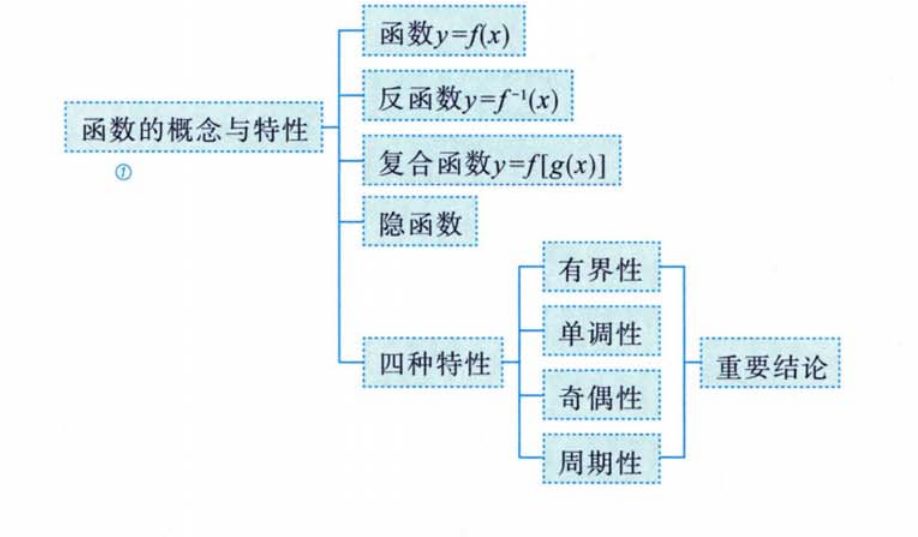
二、函数的概念
2.1函数概念
函数概念两个基本要素:定义域、对应法则
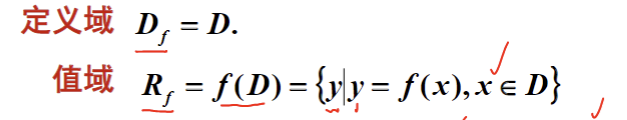
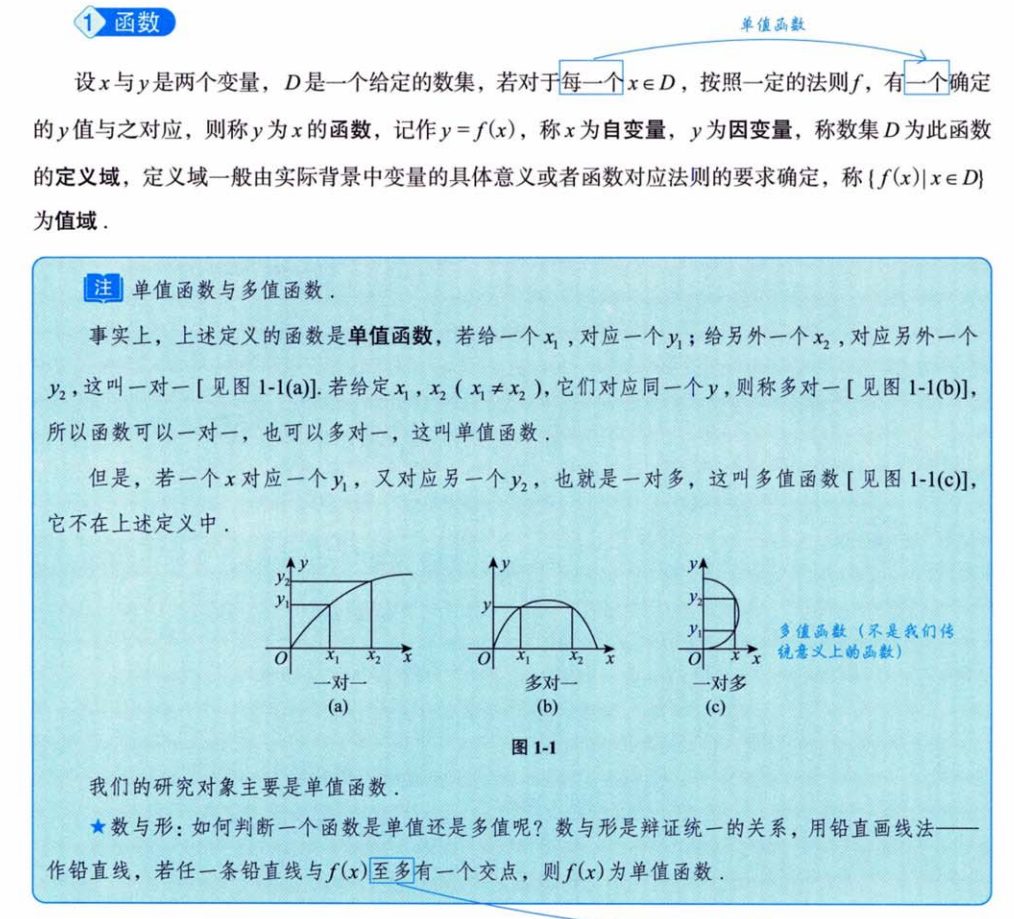
辨别单值函数、多值函数 – 铅锤划线法
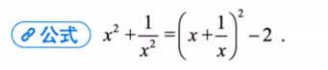

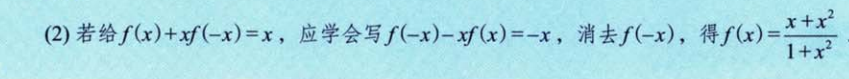
2.1.1 符号函数
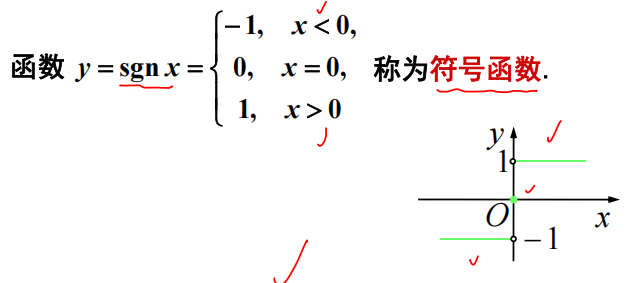
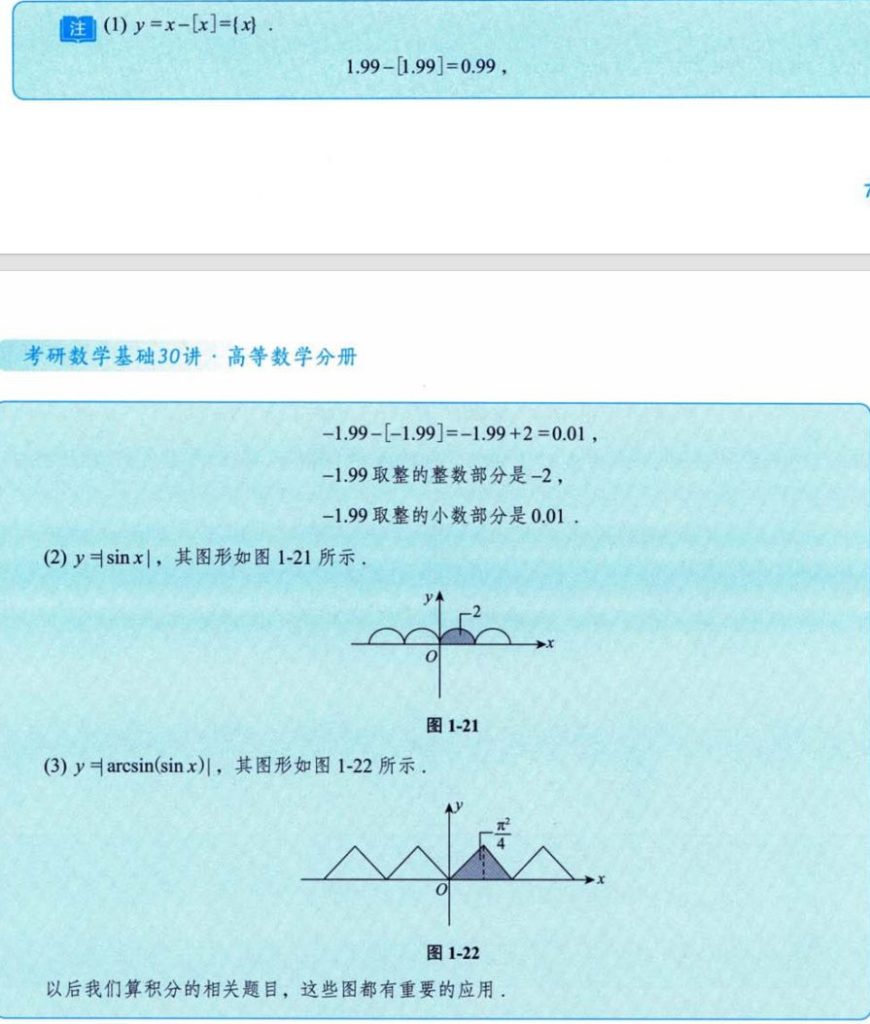
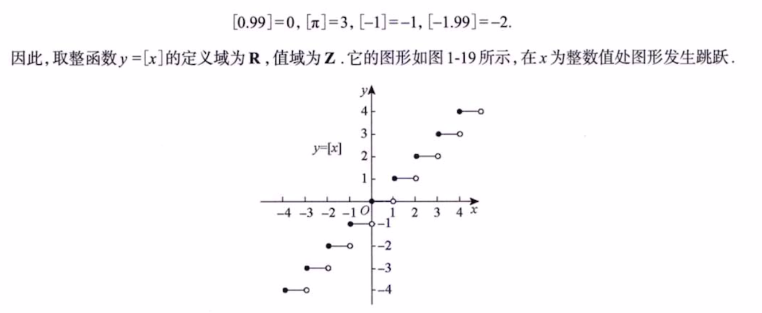
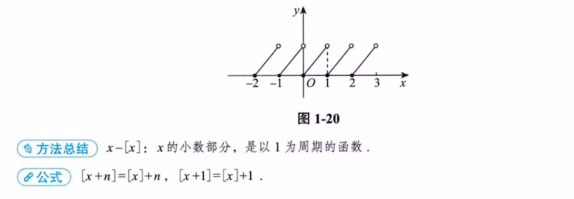
2.1.2 取整函数

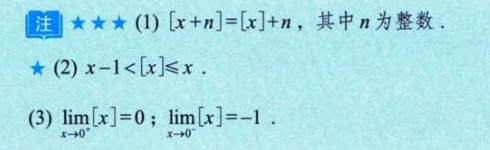
2.2反函数
前提需要符合铅锤划线法
需要知道的几个点:
1、不是每个函数都有反函数;y = x3有,y=x2没有(x2不单调)
2、单调函数一定有反函数,反之则不然,如分段函数
3、重要关系:
4、反函数的充分必要条件
5、函数与反函数互换字母后,则关于y = x对称

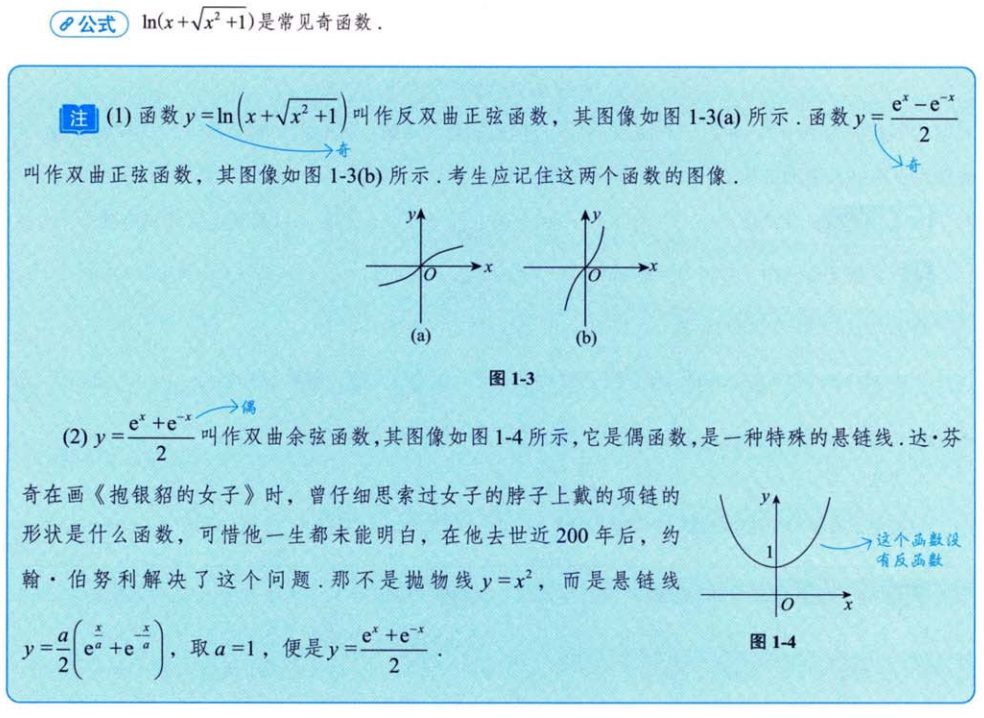
2.2.1重要的反函数

2.3 复合函数

注意 f(u) 的定义域和u = g(x)的值域的交集不能是空集
2.4 隐函数

三、函数的性质
3.1 有界性

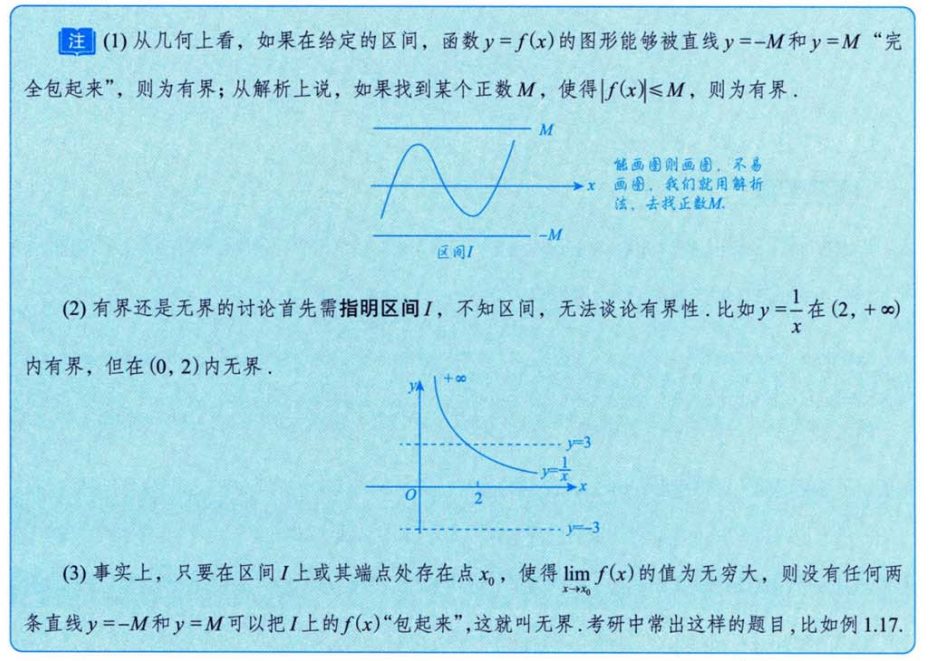
特别需要注意:讨论有界性还是无界性,需要指明区间
3.2 单调性

3.3 奇偶性



3.3.1 常见的奇函数和偶函数
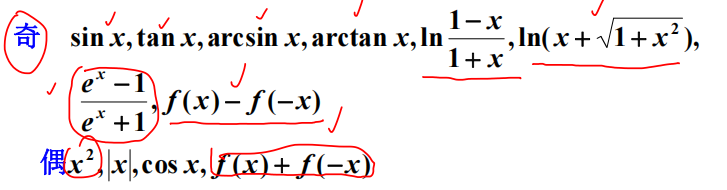
3.3.2 注意的点

3.4 周期性



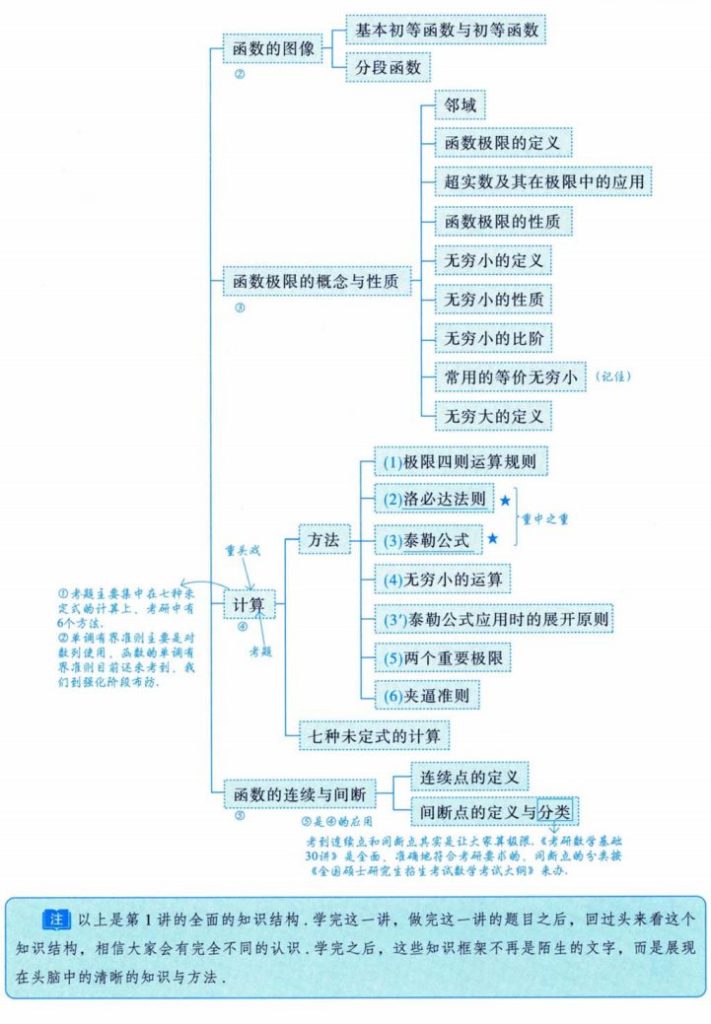
四、函数的图像
4.1初等函数

4.1.1常函数的考法 – 交点个数、求概论


4.1.2 幂函数


- 注意这个图像
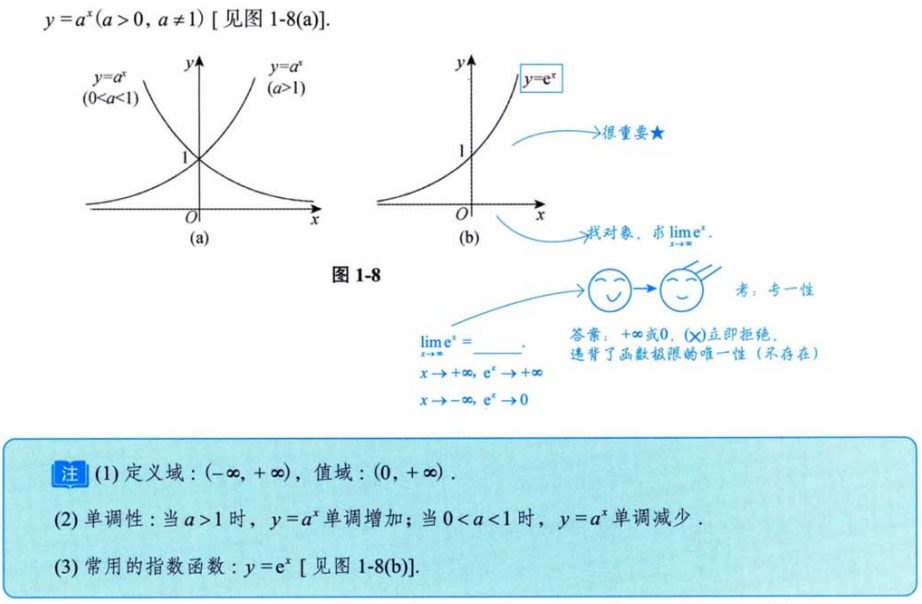
4.1.3 指数函数

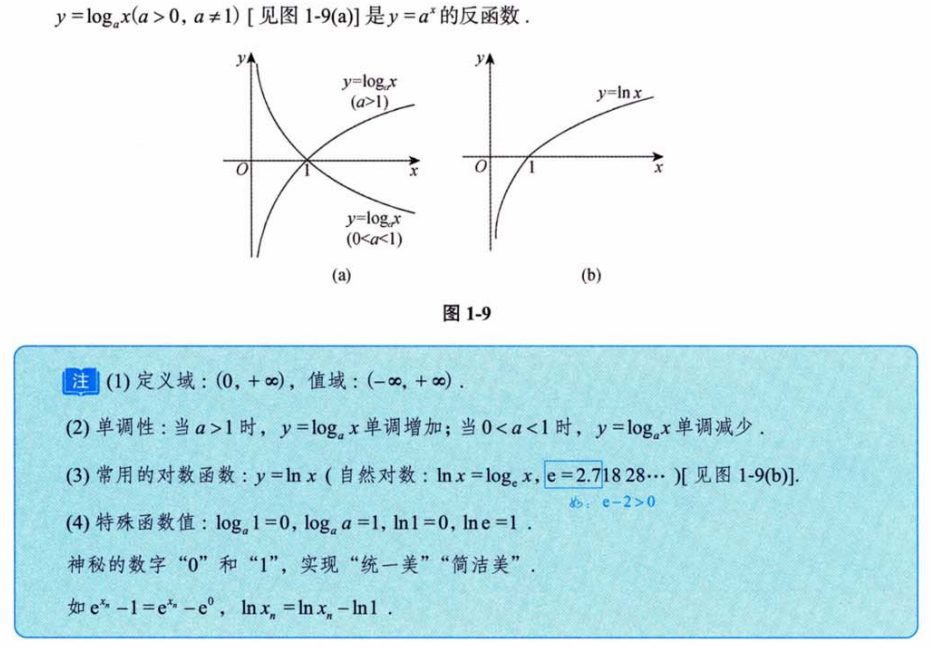
4.1.4 对数函数

4.1.5 三角函数
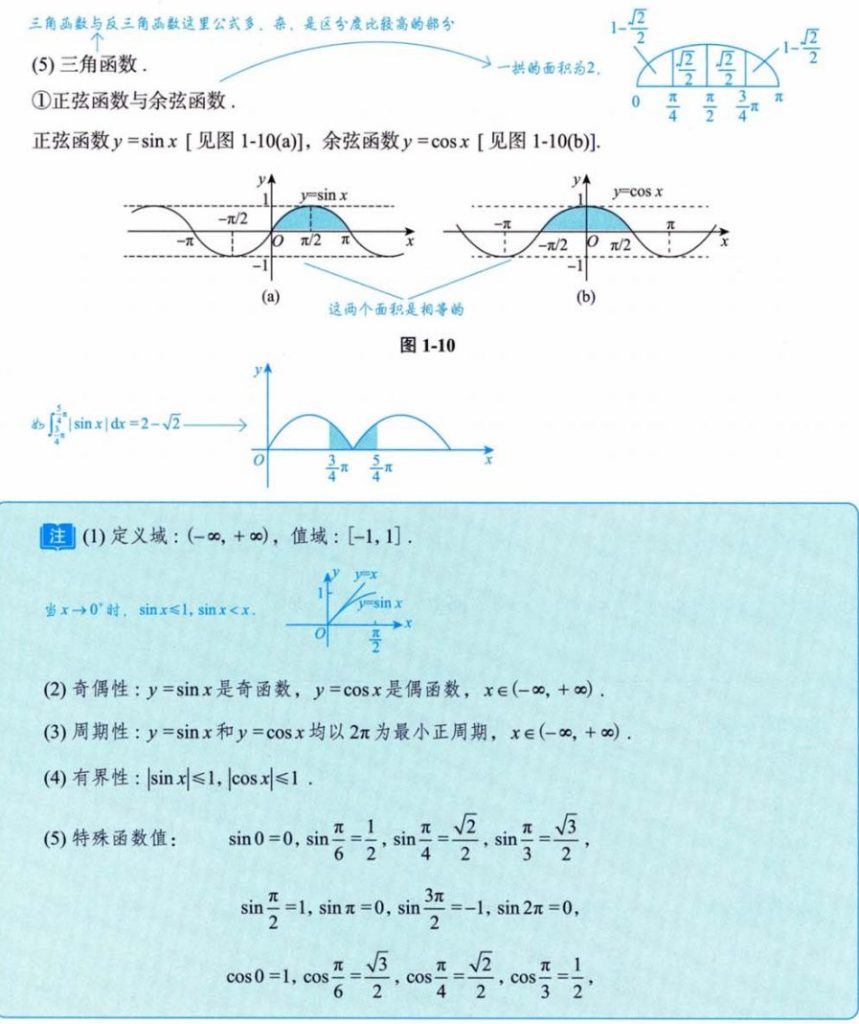

4.1.6 正切函数与余切函数

4.1.7 正割函数与余割函数
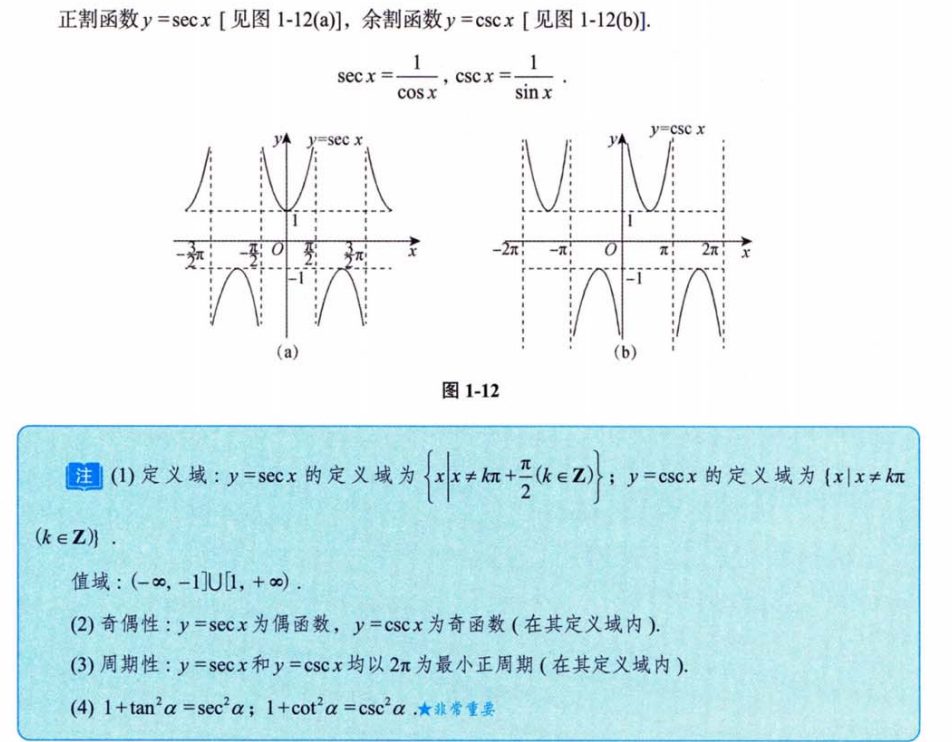
重点是最后一条,尤其在求积分的时候
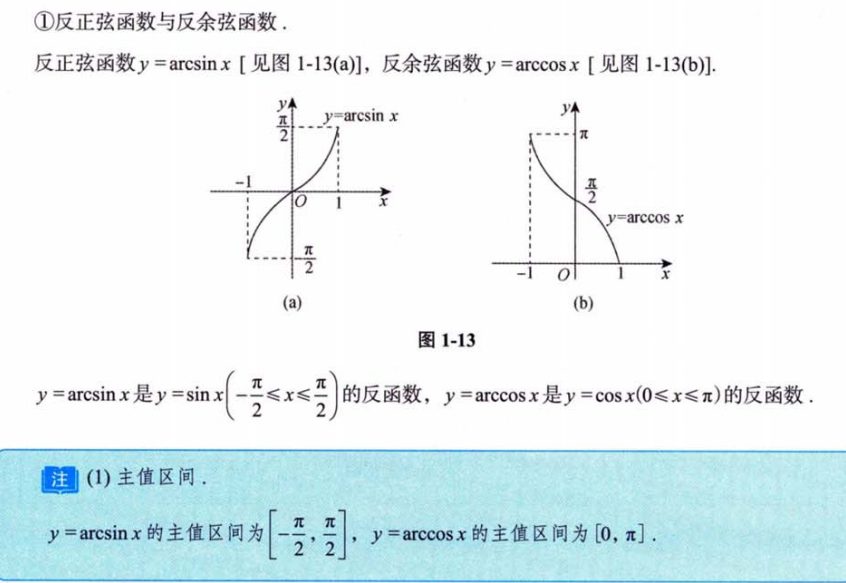
4.1.8 反三角函数

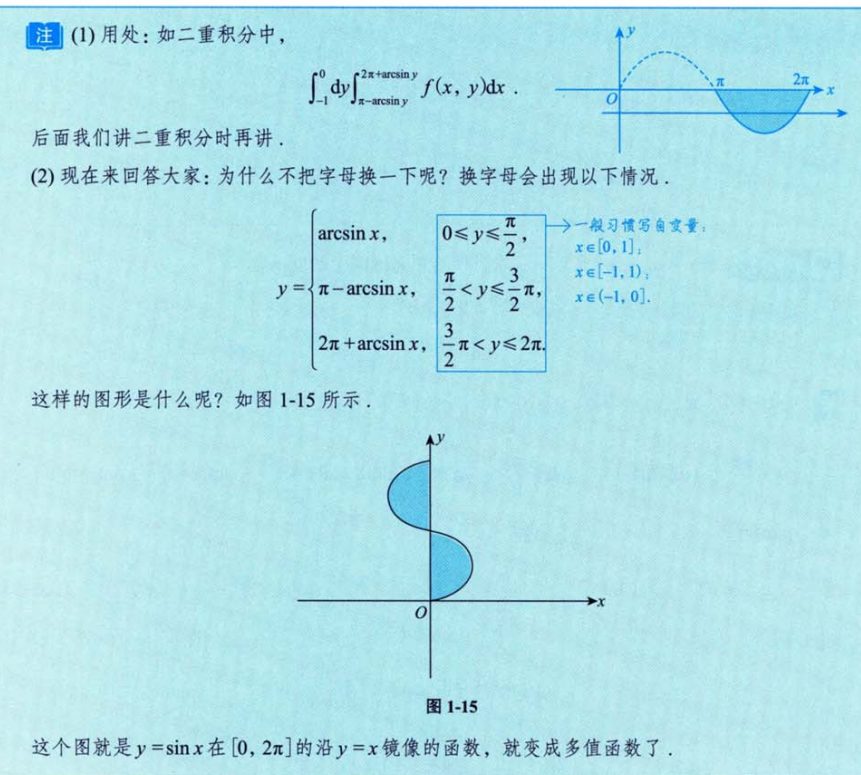
4.1.9 反正切函数与反余切函数
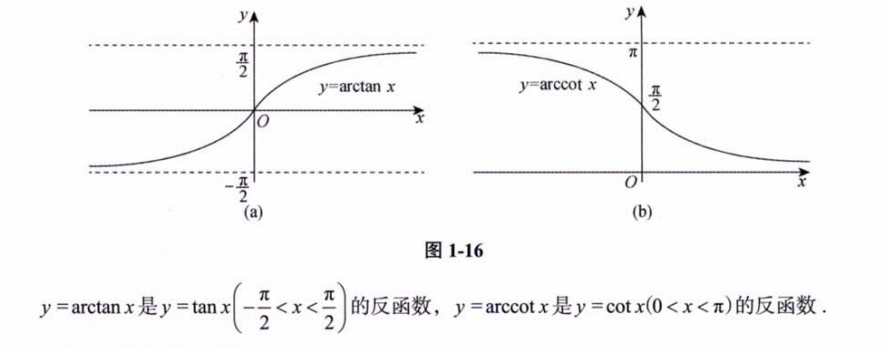

五、分段函数
2.1 分段函数形式
研究对象最多的函数 – 求极限、求导数、求积分
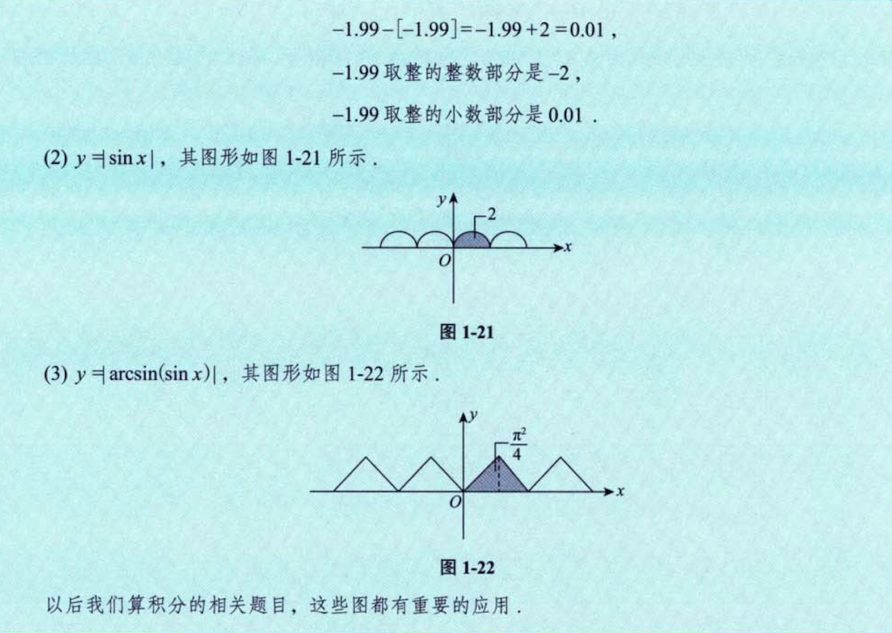
2.2 三个重要分段函数
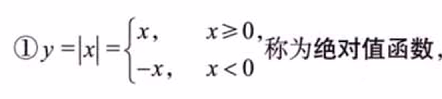
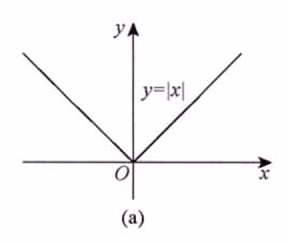




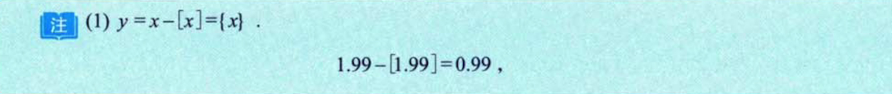
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客