一、基础知识结构
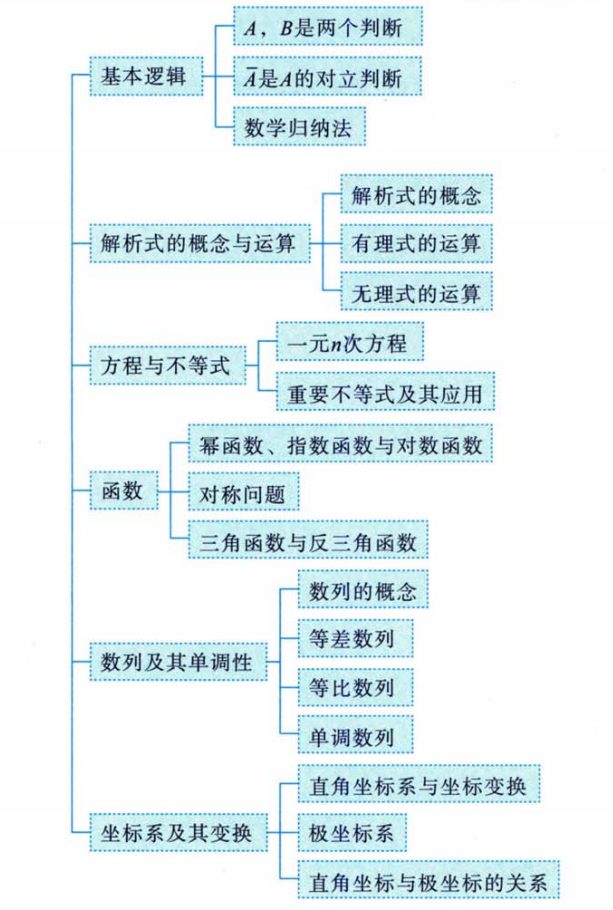
1、基本逻辑
- 考试重点:考研数学主要涉及三个方面逻辑训练
- 判断关系:A和B是两个判断,A是A的对立判断
- 数学归纳法:重要证明方法,需重点掌握
2、解析式的概念
- 定义理解:很多同学不清楚解析式的本质和结构
- 层级关系:从解析式→子标题→单项式/多项式有明确层级
- 重要性:25考生反馈显示,不了解解析式特点会导致解题困难
- 运算分类:包括有理式运算和无理式运算
3、方程与不等式
- 一元N次方程:主要研究二次、三次方程
- 根与系数:需要掌握根与系数的关系
- 不等式转化:f(x)>0f(x)>0f(x)>0或f(x)<0f(x)<0f(x)<0时转化为不等式问题
- 重要不等式:考研基础重点,需系统归纳
4、函数
- 构成方式:基本初等函数经过有限次运算或复合得到
- 反三角函数:中学阶段掌握不牢固,需重点讲解
- 常见问题:幂函数、指数函数、对数函数、三角函数的性质和计算易错
- 对称性:传统意义上的图形对称(关于线/点对称)需详细讲解
5、数列及其单调性
- 考试地位:数列是考试难点,但基本收敛问题必须掌握
- 基础内容:包括数列概念、等差数列、等比数列、单调数列、子列等
- 重要性:为后续数列收敛性研究打下基础
6、直角坐标系与坐标变换
- 主要类型:直角坐标系和极坐标系是公共考点重点
- 极坐标难点:很多同学中学阶段掌握不牢固
- 变换关系:需掌握直角坐标与极坐标的相互转化
- 应用场景:图形在不同坐标系下的表达式都需要掌握
二、函数
2.1 幂函数、指数函数与对数函数
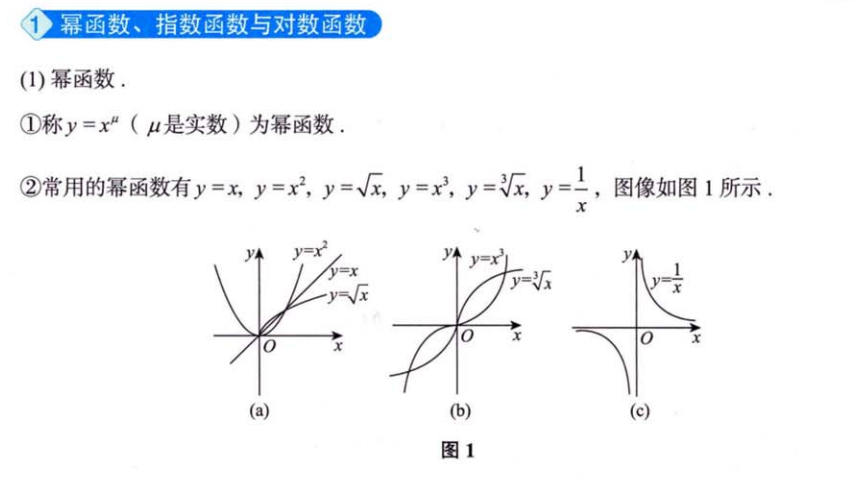
2.1.1 幂函数
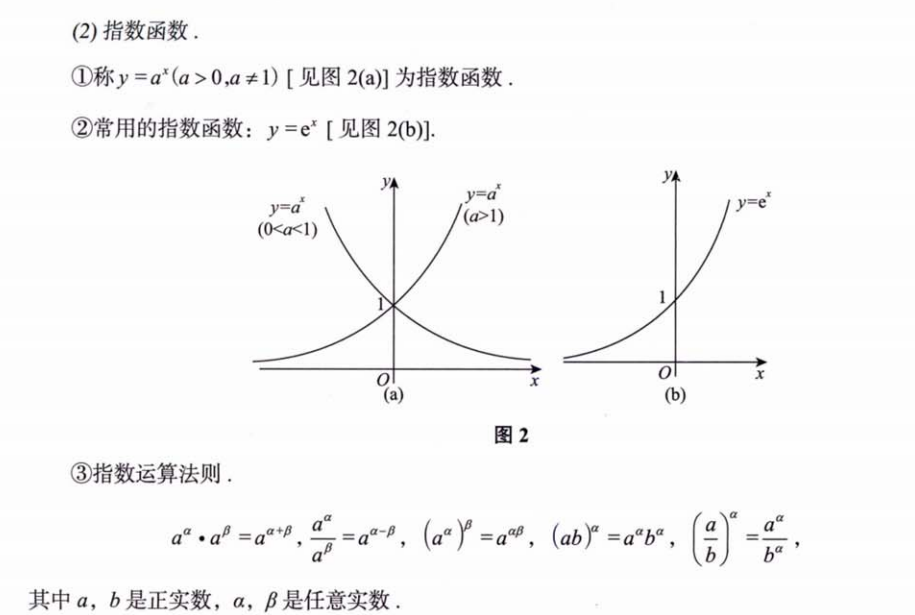
2.1.2 指数函数
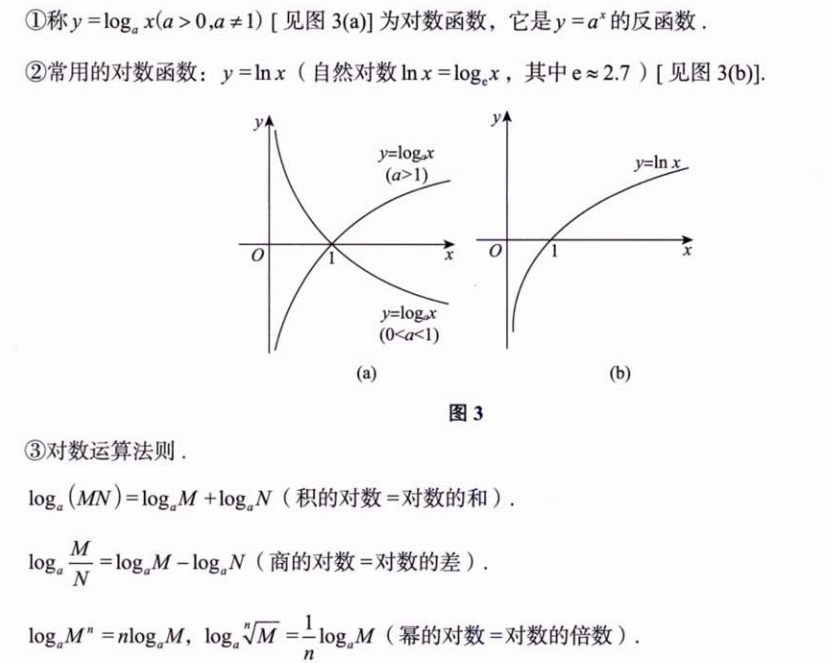
2.1.3 对数函数
2.2 对称问题
点、函数图像和方程曲线在几种常见的中心对称、轴对称变换下的情况

2.3 图像变换
图像变换方式一般有如下三种:
- 1、平移变换
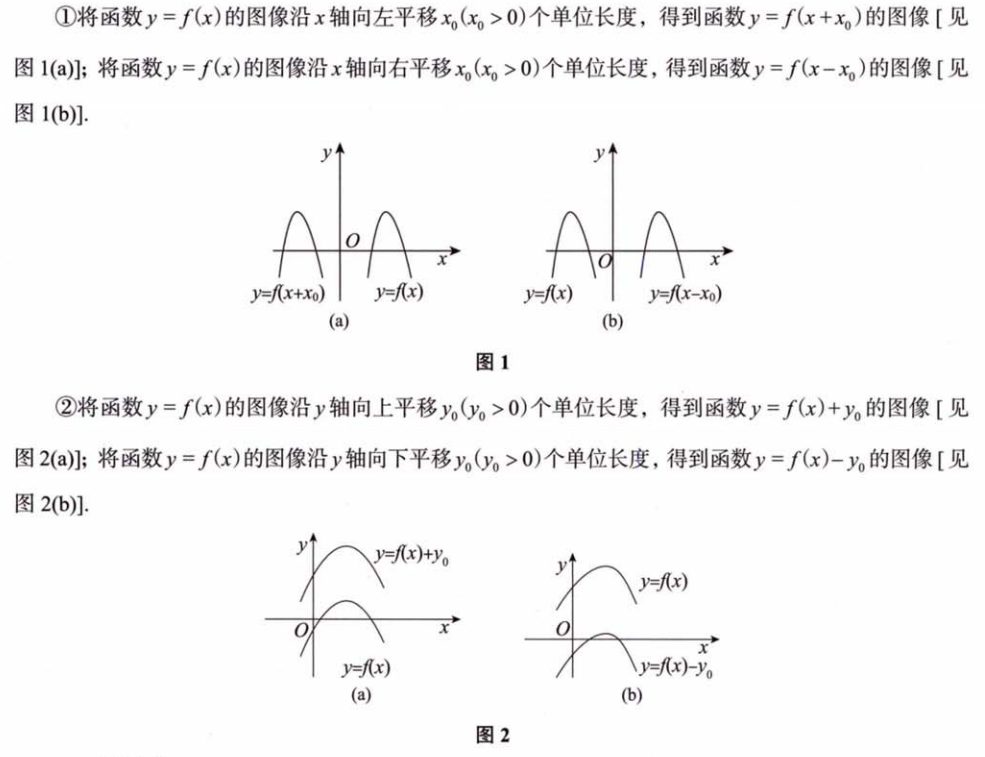
“左加右减” 的本质
- 2、对称变换

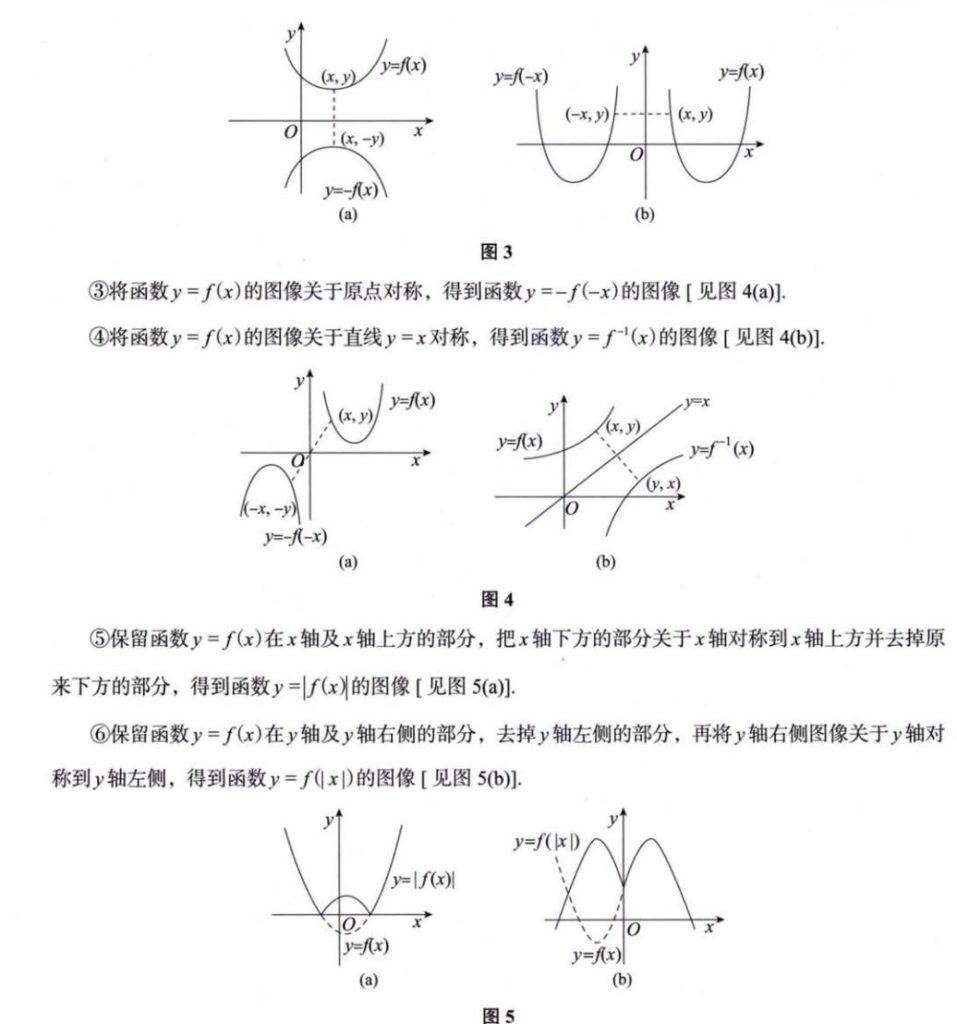


重点:2、4、6
重点关注例子
- 伸缩变换
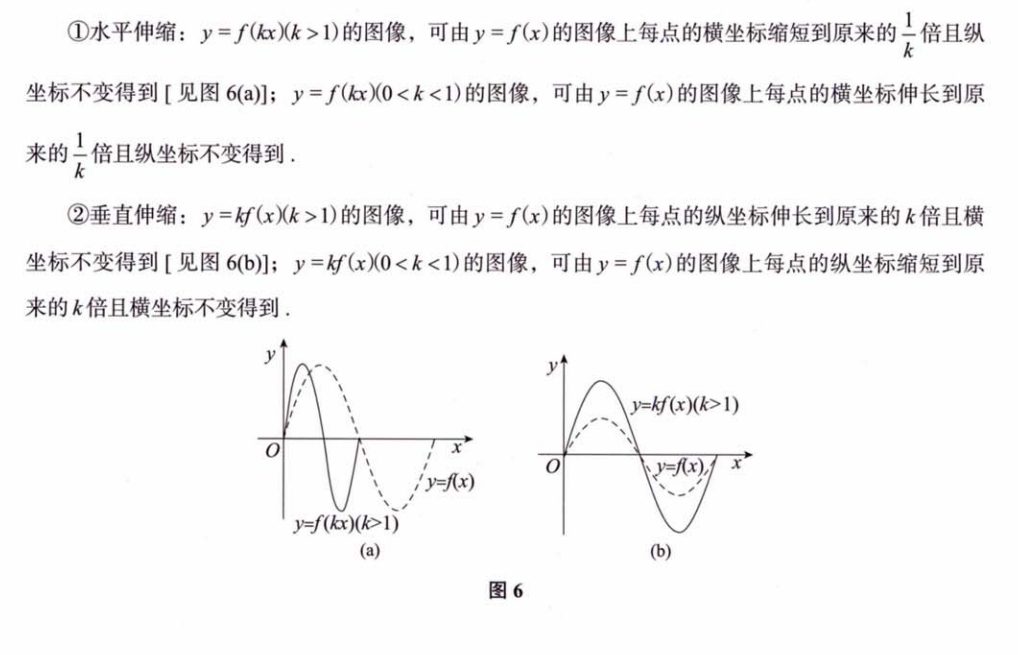
特别需要注意水平变换
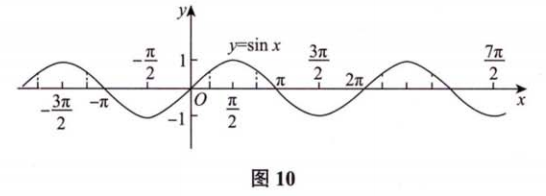
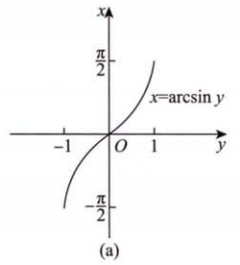
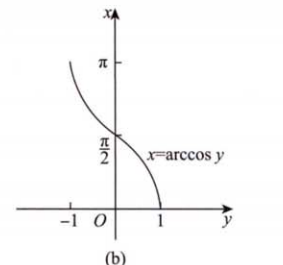
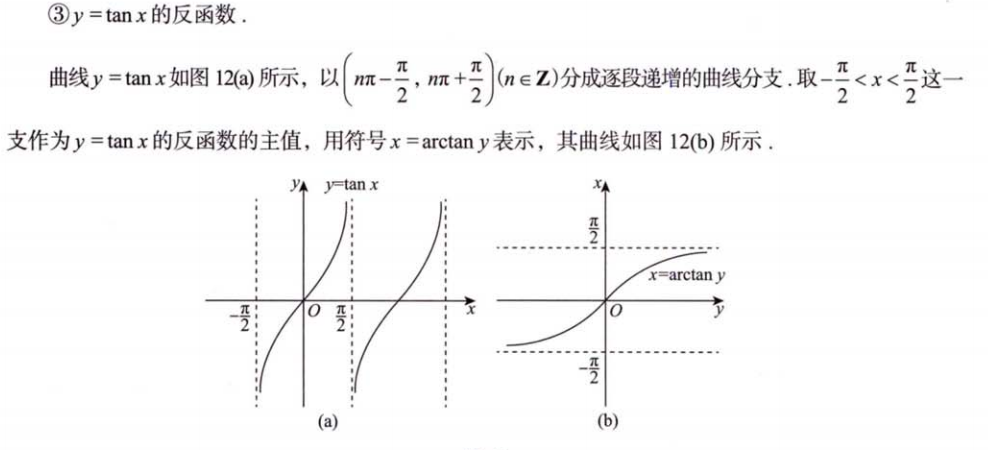
2.4 三角函数与反三角函数
- 三角函数
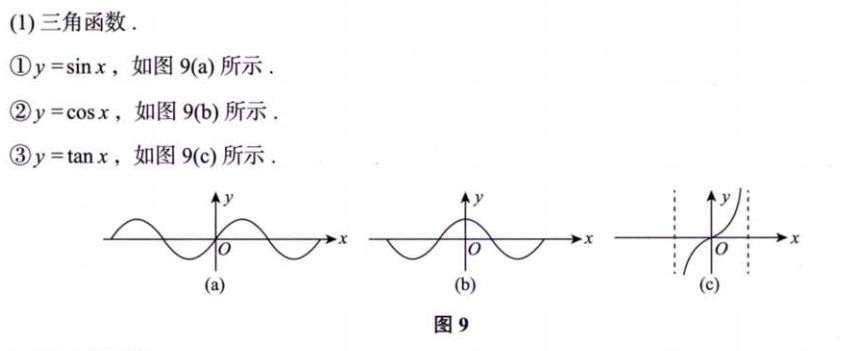
- 反三角函数


三、数列及其单调性
3.1 数列的概念

3.2 等差数列
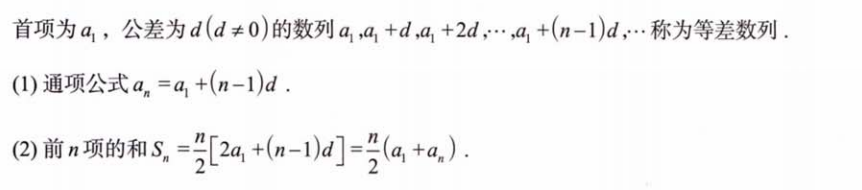
3.3 等比数列

3.4 单调数列

四、坐标系及其变换
4.1 直角坐标系与坐标变换
- 平移

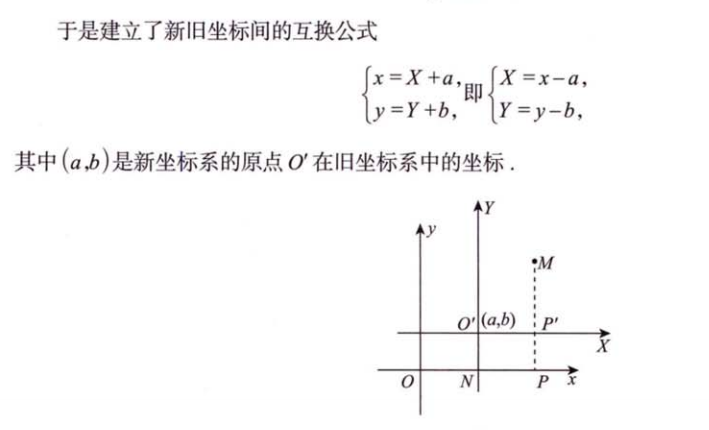

- 旋转
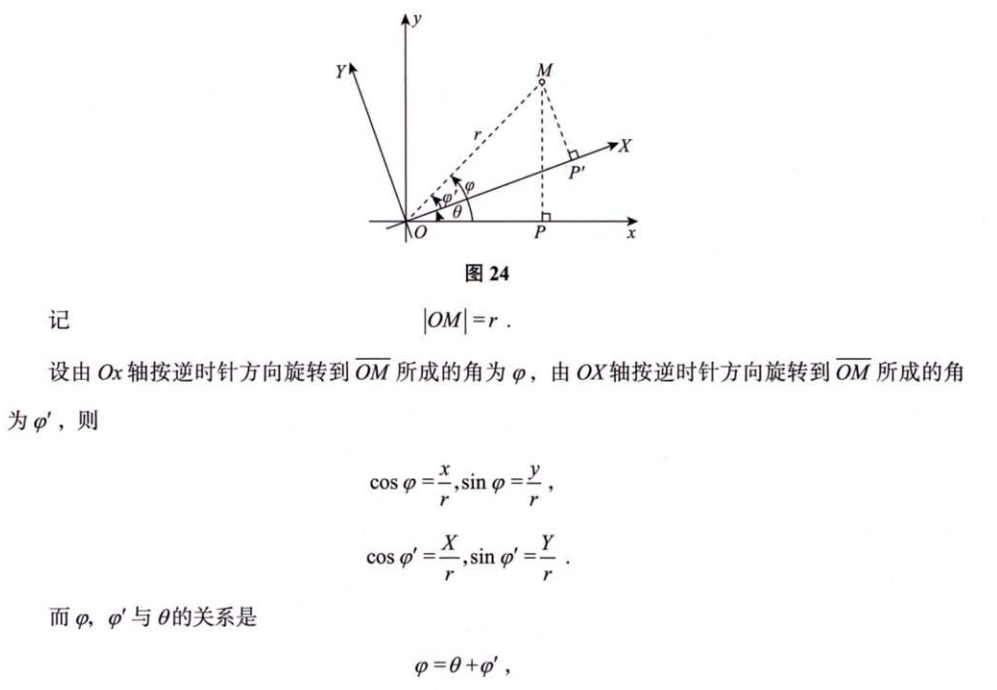
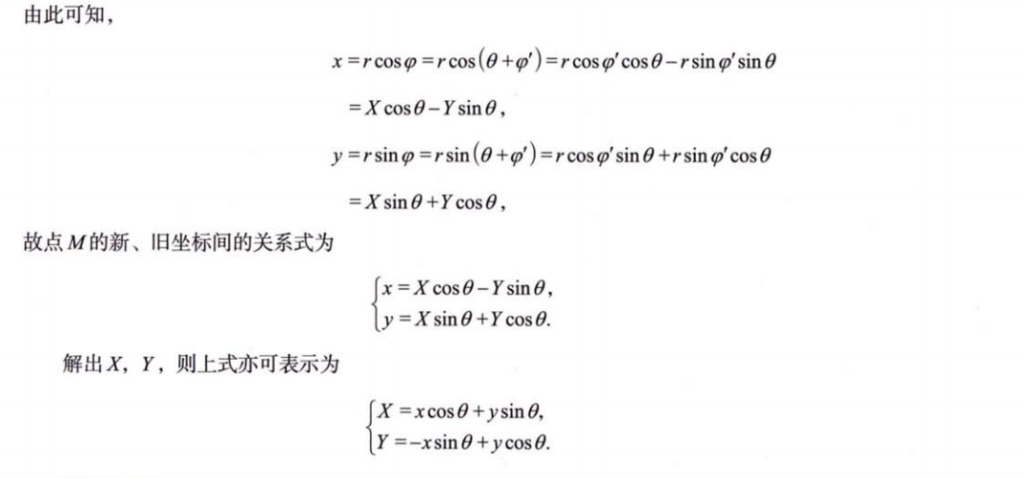
4.2 极坐标系
几种常见曲线的极坐标方程


4.3 直角坐标与极坐标的关系

本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


