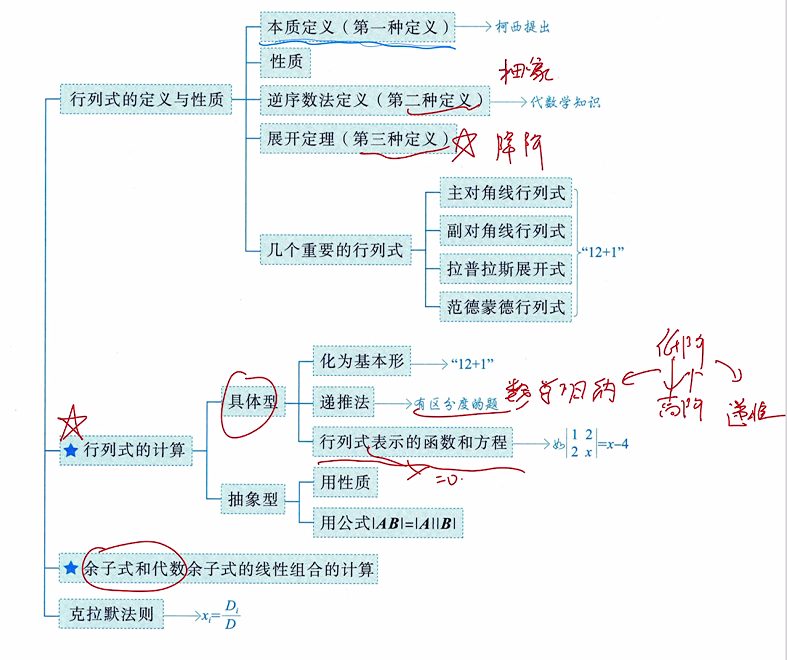
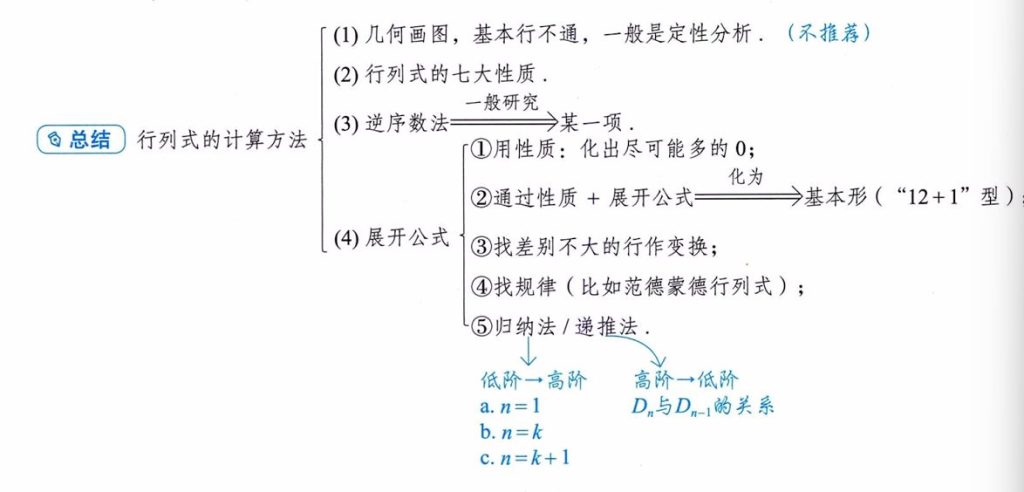
一、重要结论
1.1 行列式的本质定义(第一种定义)
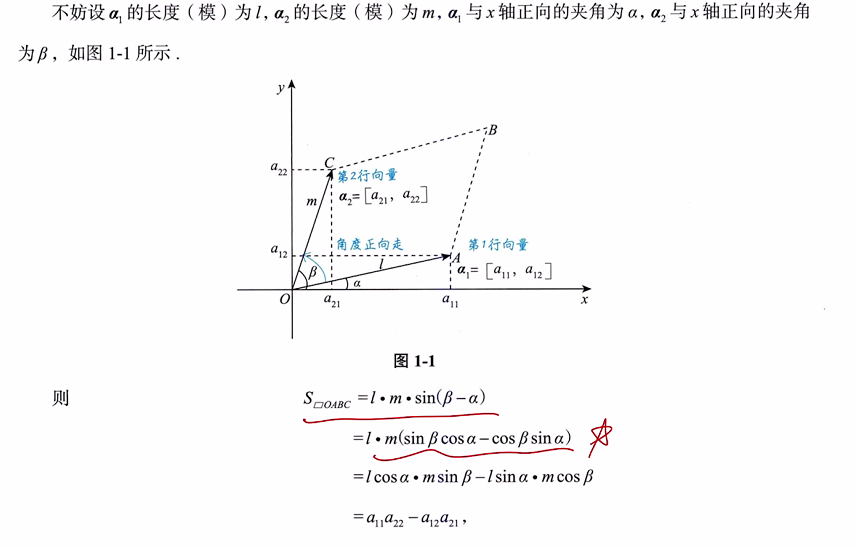
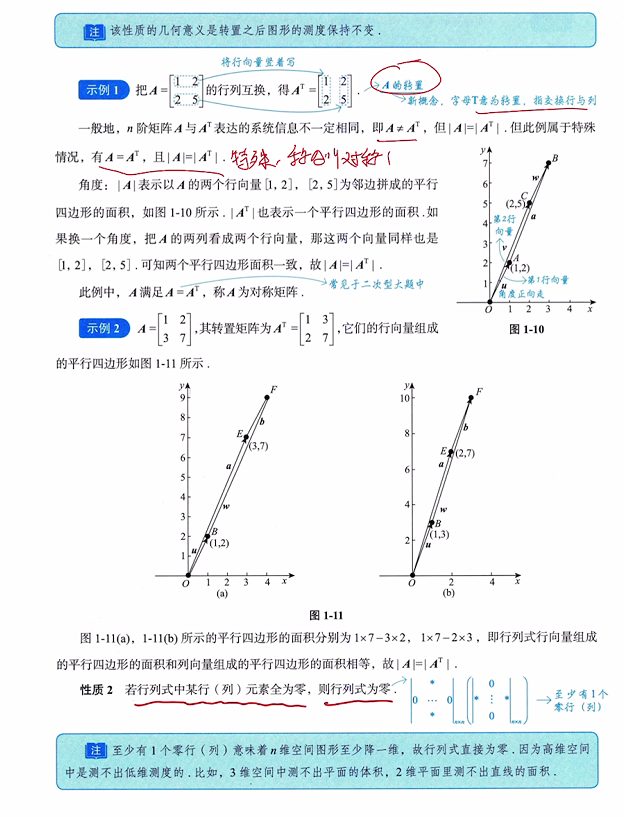
1、2阶行列式是由两个2维向量组成的,其(运算规则的)结果为以这两个向量为领边的平行四边形的面积
2、代数学中的面积可以是负值
3、若行列式两行或者两列成比例,则行列式为0
4、行列式若一行或一列为0,则行列式为0
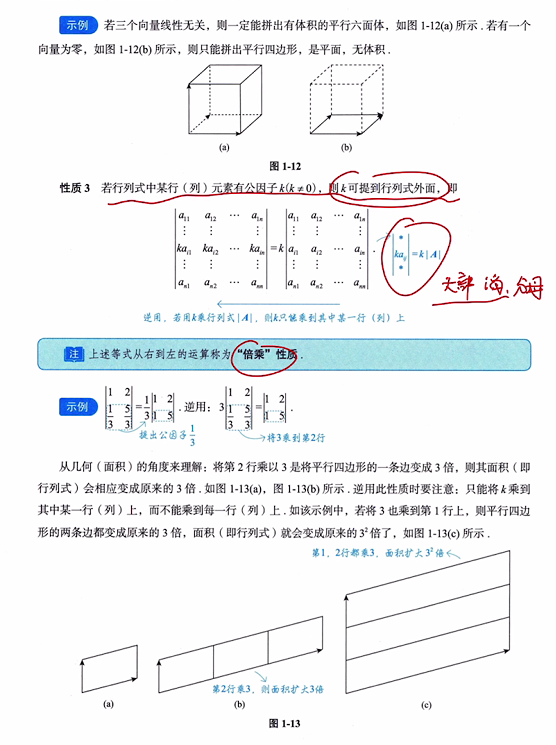
5、3 阶行列式是由三个3维向量组成,其(运算规则的)结果为以这三个向量为邻边的行六面体的体积
6、n(n≥3)阶行列式是由n个n维向量组成的,其结果是以这n个向量为邻边的n维图像的体积
7、D3 ≠ 0 , 组成行列式的三个向量线性无关, D3 = 0,则称线性相关
1.2 行列式的性质
1、行列式互换,其值不变,即 | A | = | AT |
2、若行列式中某行(列)元素全为零,则行列式为零
3、若行列式中某行(列)元素有公因子 k (k≠0),则 k 可提到行列式外面
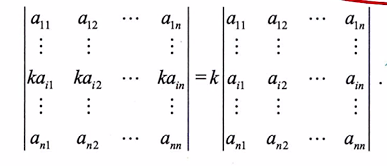
- 逆用,若用 k 乘行列式|A|,则 k 只能乘到其中某一行(列)上
- 注意 k |A|,KA的区别
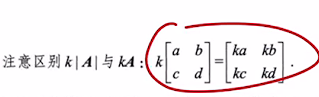
4、行列式中某行(列)元素均是两个数之和,则可拆成两个行列式之和,即
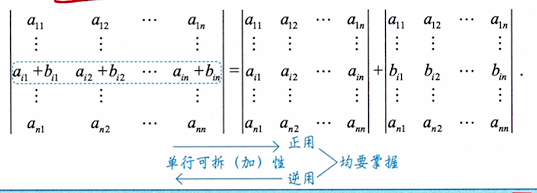
- 易错点

5、行列式两行(列)互换,行列式变号
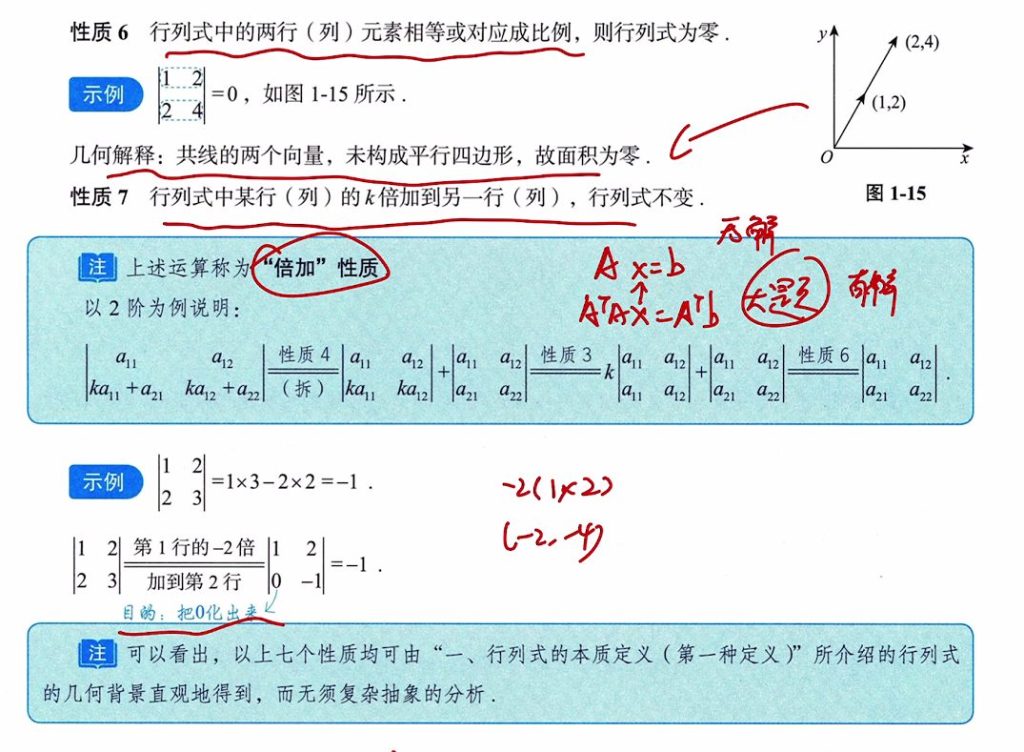
6、行列式中两行(列)元素相等或对应成比例,则行列式为零
7、行列式中某行(列)的 k 倍加到另一个行(列),行列式不变

1.3 行列式的逆序数法定义(第二种定义)
1、排列:n个数1,2,3,4,5….n 组成的一个有序数称为一个n级排列,n 级排列有n!个
2、逆序:排前面的数大于排后面的数
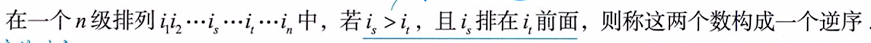
3、逆序数:一个排列中,逆序的总数称为该排列的逆序数

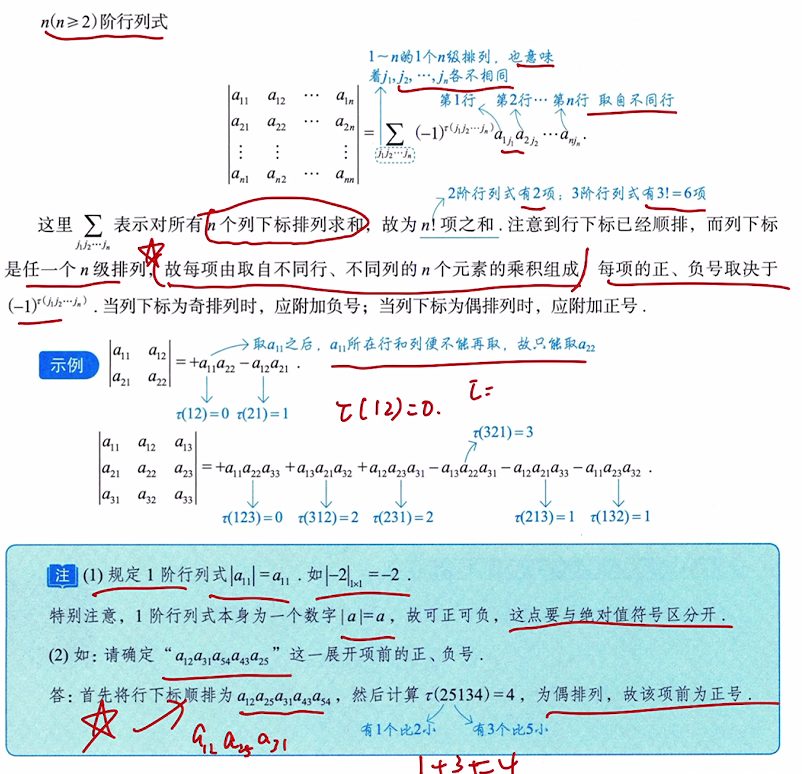
4、奇排列和偶排列:排列的逆序数为奇数时,该排列称为奇排列;排列的逆序数为偶数时,该排列称为偶排列;对于 n 阶行列式定义中,奇排列,加负号;当列下标为偶排列时,应附加正号

1.4 行列式的展开定理(第三种定义)
1、余子式(行列式)
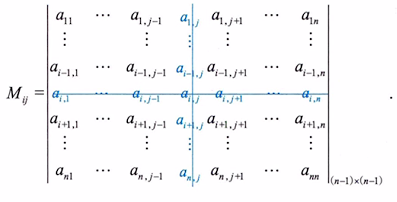
2、代数余子式

3、行列式按某一行(列)展开的展开公式:找0元素最多的行进行展开
1.5 几个重要的行列式
1、主对角线行列式(上(下)三角形行列式):
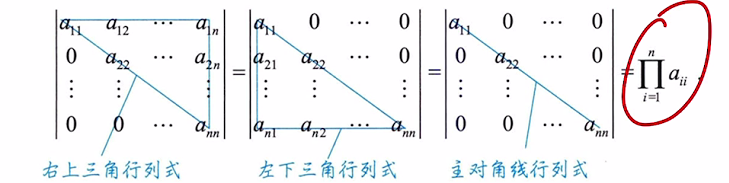
2、副对角线行列式
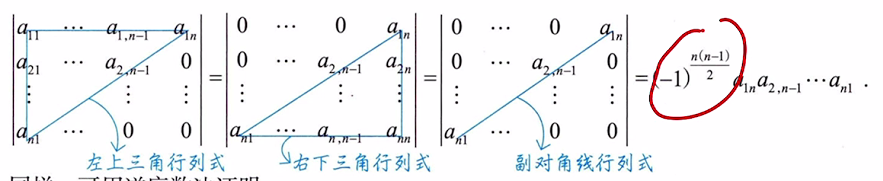
3、拉普拉斯展开式

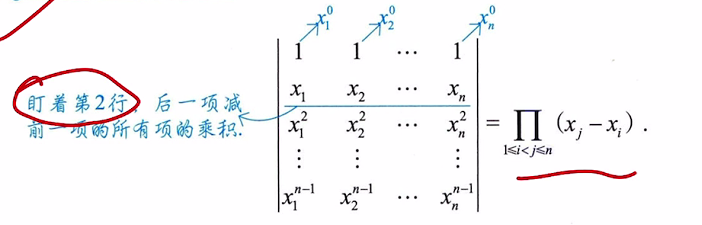
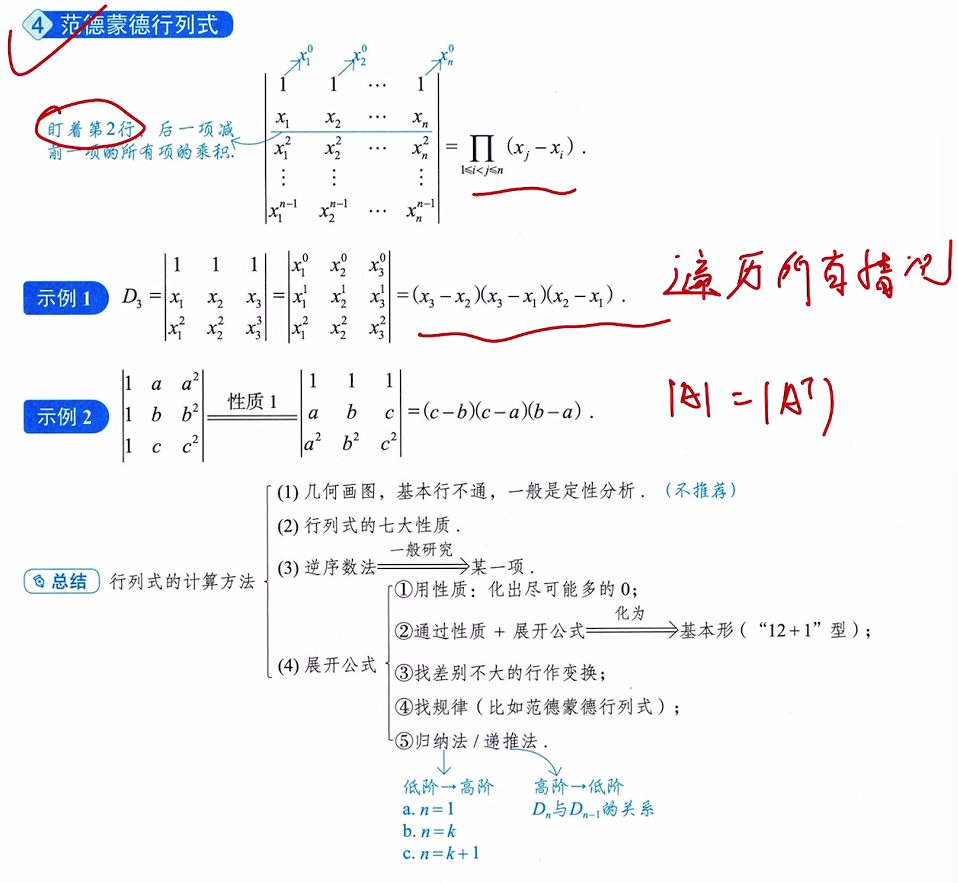
4、范德蒙德行列式:遍历第二行
二、行列式的本质定义(第一种定义)



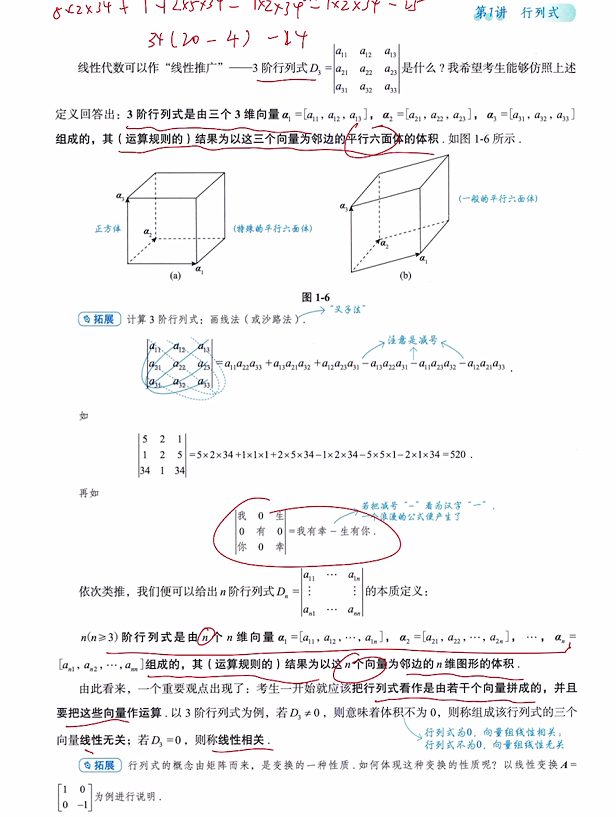

三、行列式的性质
研究几何测度


四、行列式的逆序数法定义(第二种定义)
4.1 排序和逆序

4.2 n 阶行列式的定义
五、行列式的展开定理(第三种定义)
降阶思想:对于阶数大于3的行列式
5.1 余子式


5.2 代数余子式

5.3 行列式按某一行(列)展开的展开公式

六、几个重要行列式
6.1 主对角线行列式(上(下)三角形行列式)
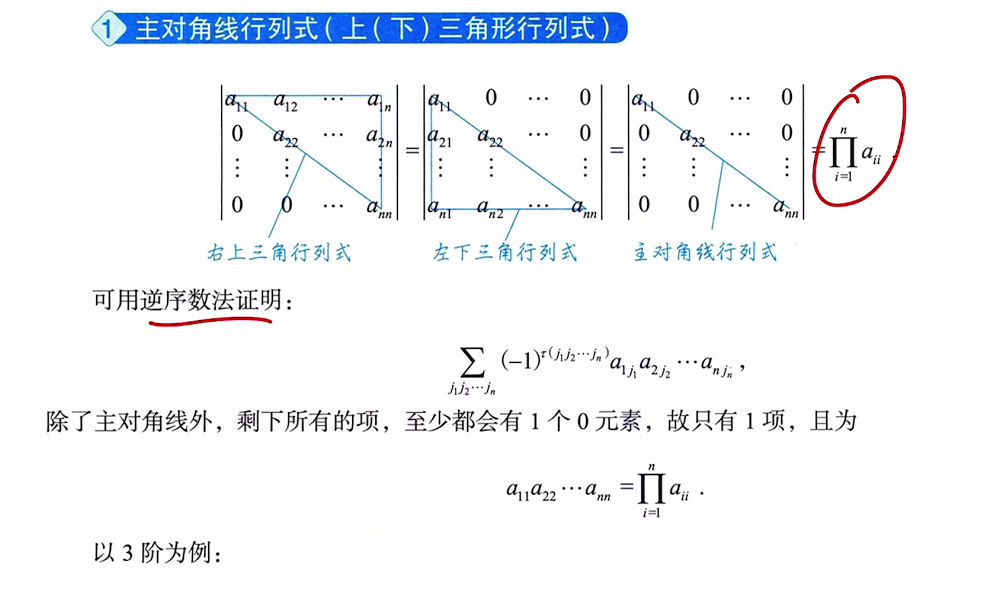
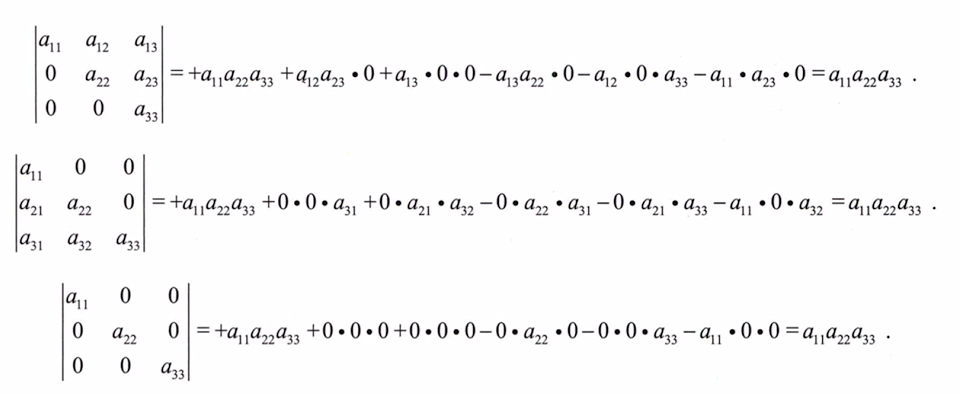
6.2 副对角线行列式
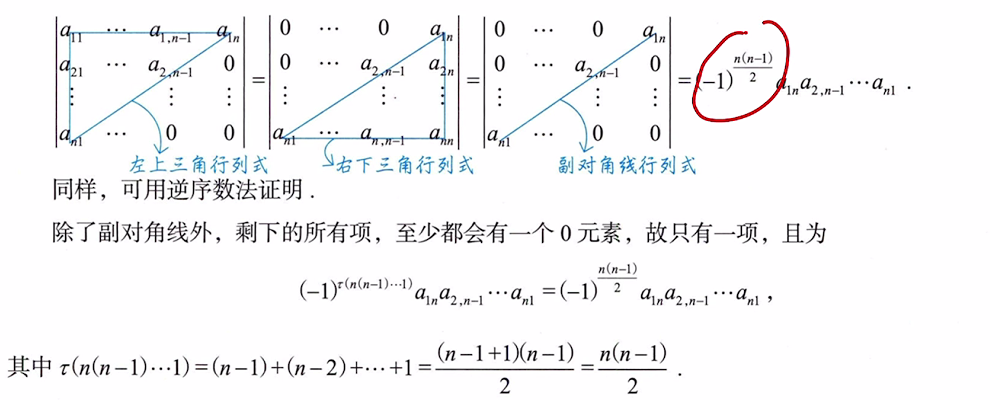
6.3 拉普拉斯展开式(分块求矩阵)
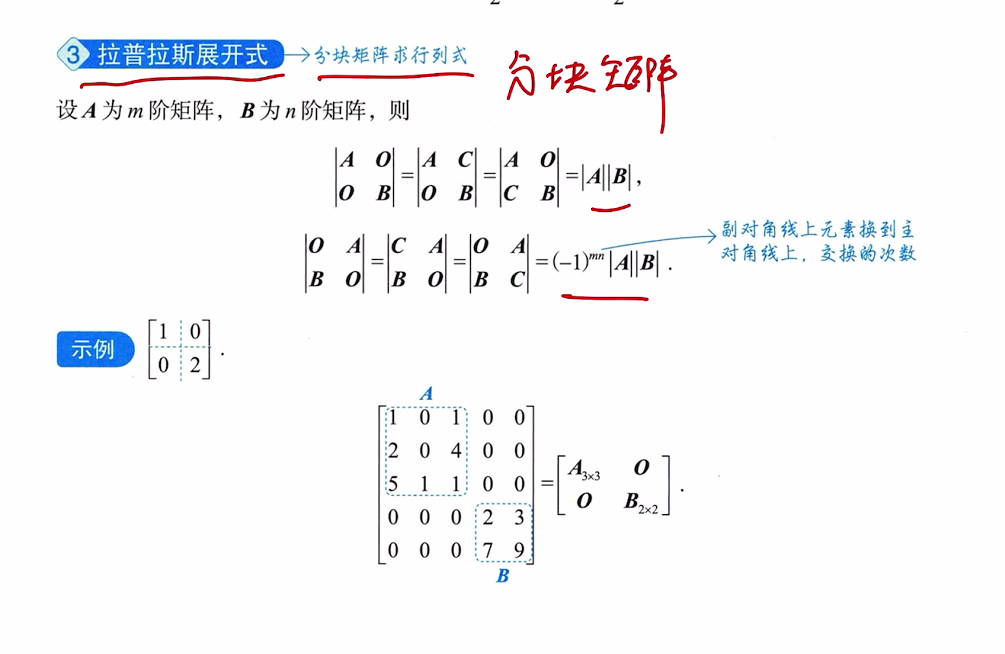
6.4 范德蒙德行列式
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


