一、数字电路基础知识 – 逻辑门电路

1.1 算数运算vs逻辑运算
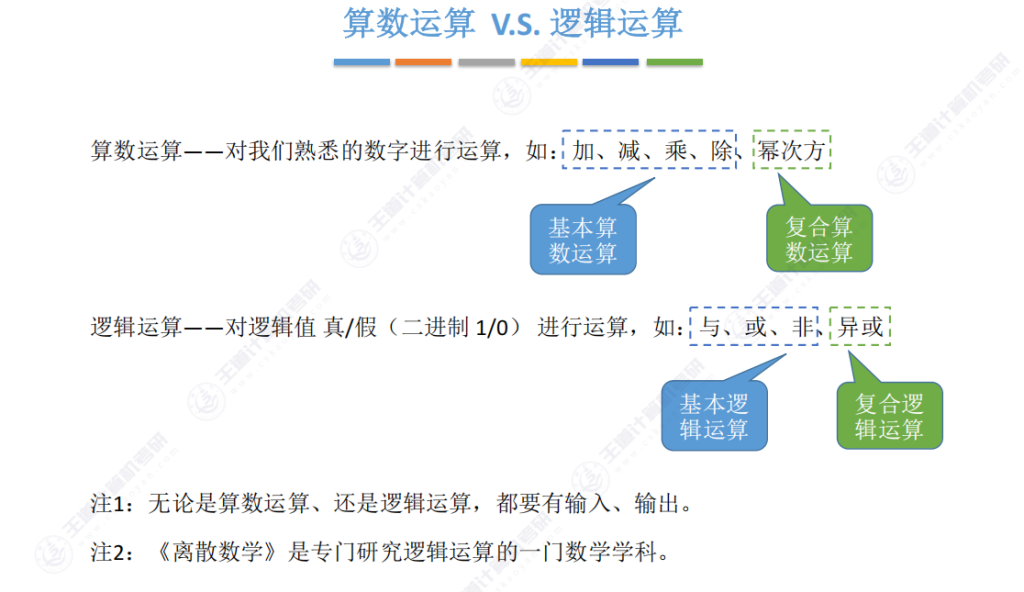
- 运算对象区别:
- 算术运算:处理实数(如1.5,-3.2等)
- 逻辑运算:仅处理二进制值(0/1,对应假/真)
- 基本运算对比:
- 算术基本运算:加、减、乘、除
- 逻辑基本运算:与、或、非
- 复合运算原理:
- 幂次方可拆解为多次乘法(如x3=x×x×x)
- 异或运算可由与或非组合实现
- 输入输出特性:
- 算术运算示例:a+b=c中a,b为输入,c为输出
- 逻辑运算示例:1和0进行与运算,结果为输出
1.2 基本逻辑运算:与
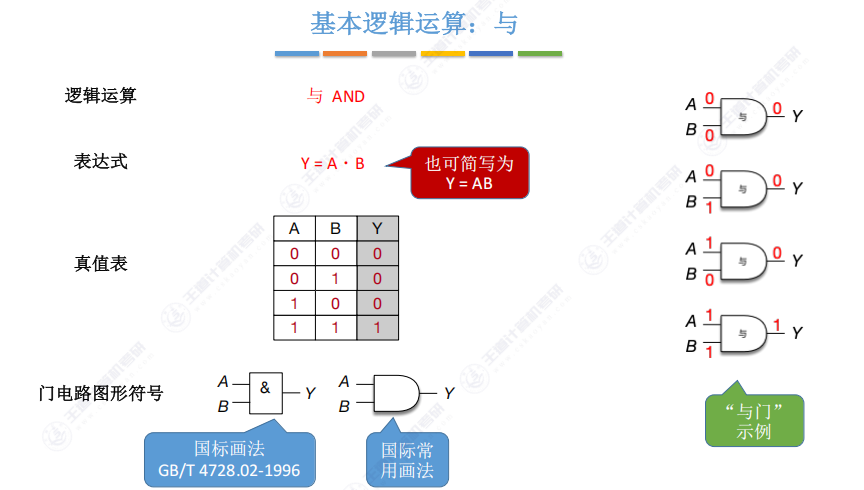
- 运算规则:仅当A、B同时为1时输出1(全真为真)
- 门电路特征:
- 国标画法:方框内写”&”
- 国际画法:输入端为直线,输出端为圆弧
- 编程对应:与C语言的”&&”逻辑相同
- 简化表示:可省略运算符点(如Y=AB)
1.3 基本逻辑运算:或
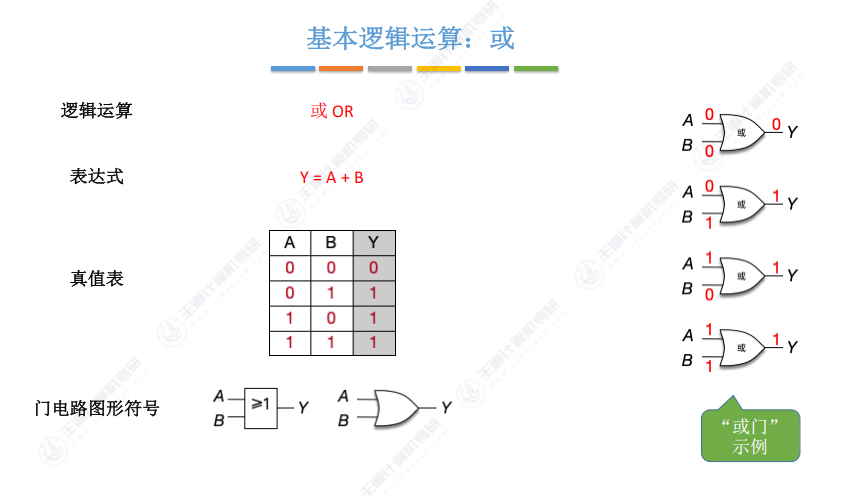
- 表达式:Y=A+B(“+”读作”或”)
- 运算规则:A、B有任一为1则输出1(一真即真)
- 门电路特征:
- 输入端为弧线(区别于与门的直线)
- 输出端形状可变但输入弧线是识别关键
- 编程对应:与C语言的”||”逻辑相同
- 特殊情况:仅当A=B=0时输出0
1.3 基本逻辑运算:非
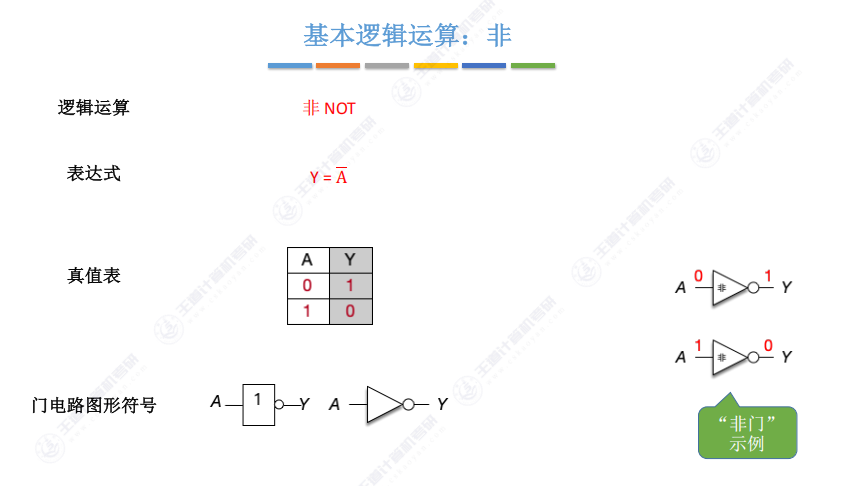
- 运算规则:输出与输入相反(0变1,1变0)
- 门电路特征:
- 必含小圆圈(可以在输入或输出端)
- 单输入特性:唯一只需一个输入的基本逻辑运算
1.4 复合逻辑运算:与非
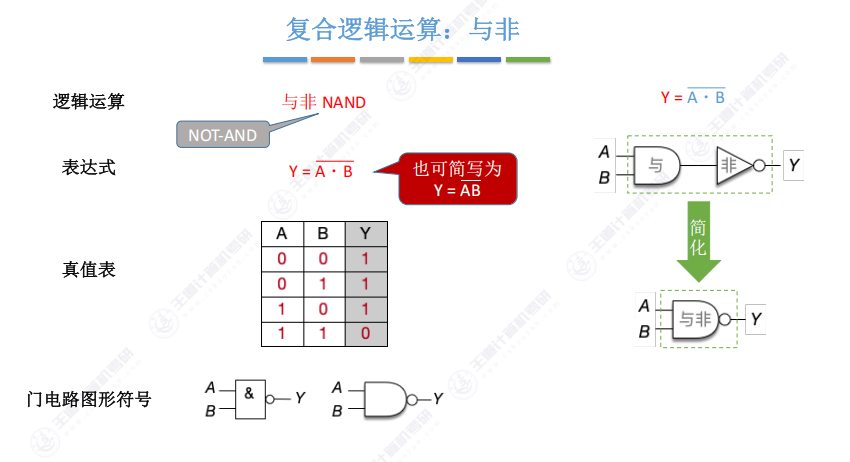
- 实现原理:与门后接非门(可简化为与门输出加圆圈)
- 运算特点:与运算结果取反(全1得0,其余得1)
- 电路简化:实际使用合并符号”与非门”替代级联电路
1.5 复合逻辑运算:或非
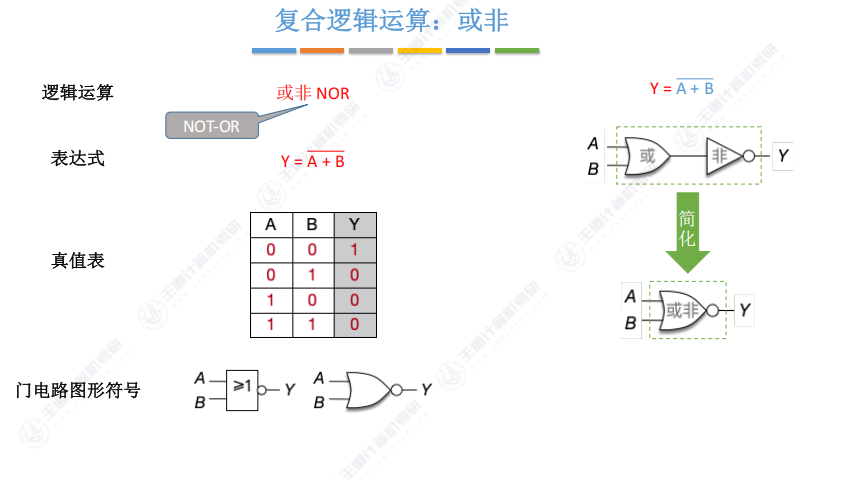
- 实现原理:或门后接非门(简化为或门输出加圆圈)
- 运算特点:或运算结果取反(全0得1,其余得0)
- 命名规律:NOT+OR→NOR(注意与与非的顺序区别)
1.6 复合逻辑运算:异或(exclusive OR)
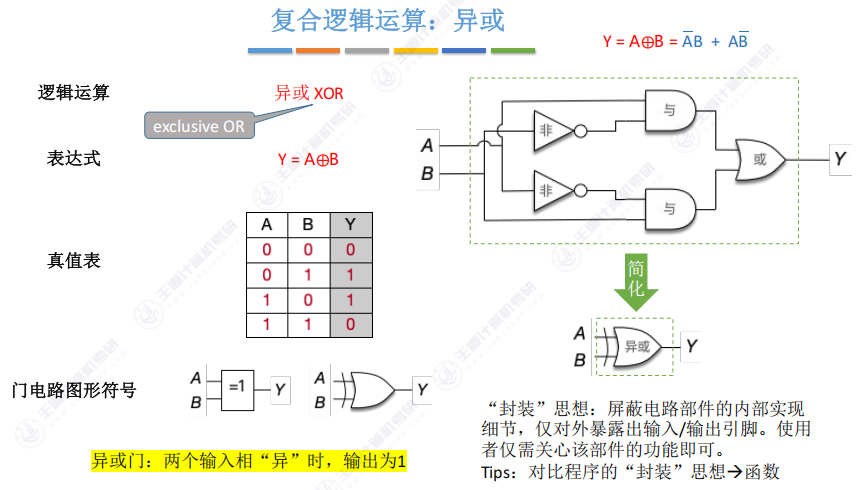
- 表达式:Y=A⊕B
- 运算规则:输入相异输出1,相同输出0
- 实现原理:通过基本门组合实现
- 门电路特征:
- 类似或门但输入端有附加弧线
- 封装思想:复杂电路简化为标准符号(类比编程函数封装)
n 个比特bit 进行异或,若有奇数个1,则异或结果为 1;若有偶数个1,则异或结果为0
验证方法:可通过逐位异或验证给定比特串中1的个数奇偶性

- 应用领域:
- 奇校验电路设计
- 二进制加法器实现
- 数据校验模块开发
1.7 复合逻辑运算:同或(异或非)- exclusive NOT-OR
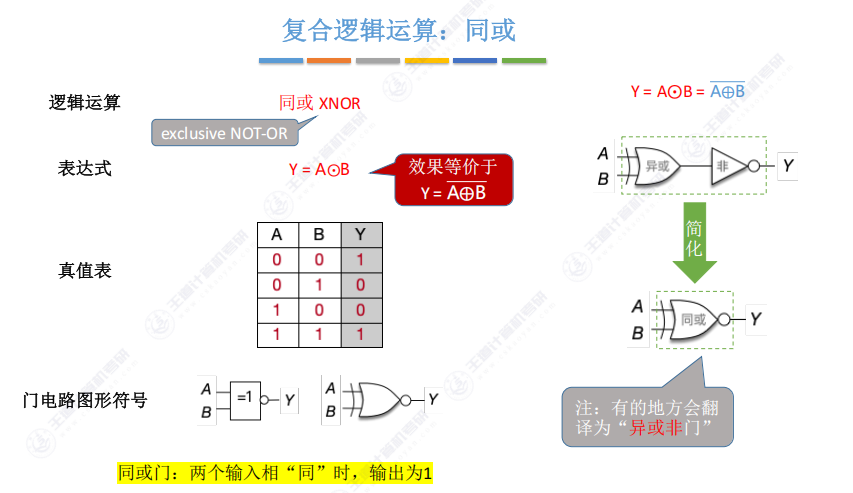
- 别名:异或非(XNOR)
- 运算规则:与异或相反(输入相同输出1,相异输出0)
- 实现原理:异或门后接非门(简化为异或门输出加圆圈)
- 门电路特征:异或门符号基础上输出端增加小圆圈
1.8 逻辑门电路知识总结
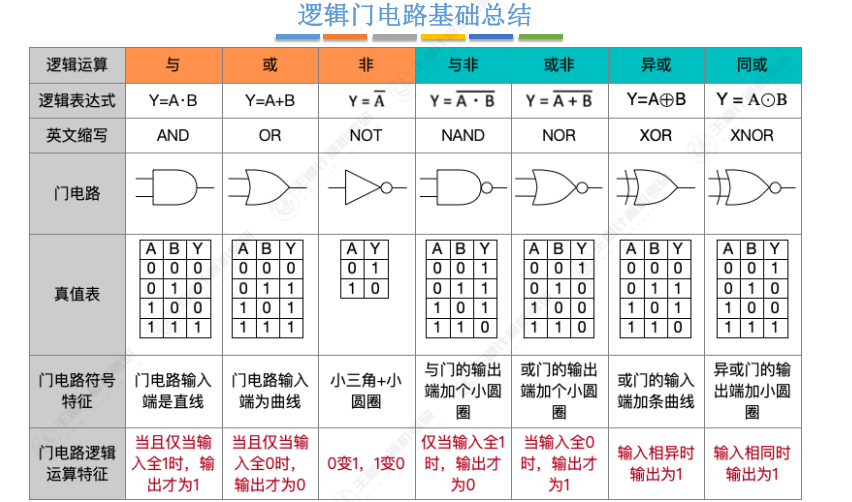
门电路的变形画法
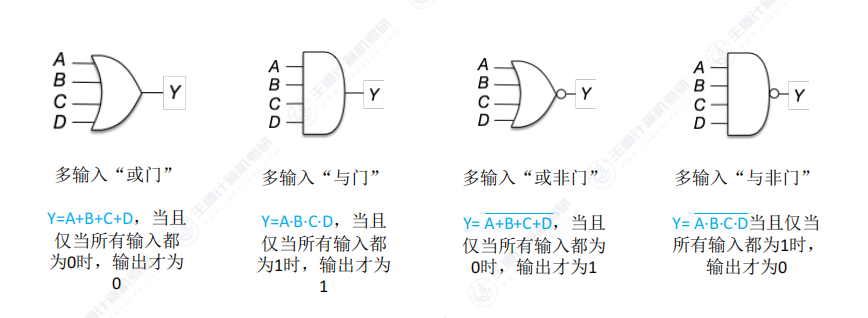
重点掌握画图和门电路逻辑运算特征
1.9 逻辑运算的优先级、常见公式

三种基本逻辑运算的优先级:非>与>或
电路设计应用:通过公式化简可优化电路结构,例如用分配律将3个门电路简化为2个
1.10 补充:芯片制程

- 制程定义:指晶体管栅极宽度(如10nm制程即栅极宽10nm)
- 技术影响:
- 制程越小→晶体管尺寸越小
- 单位面积晶体管数量更多→实现更复杂功能
- 功耗更低
- 尺寸对比:10nm是头发丝直径(0.1mm=100,000nm)的1/10000
- 关键设备:荷兰ASML公司生产的光刻机是实现纳米级制程的核心设备
二、数字电路基础知识 – 多路选择器&三态门
2.1 多路选择器
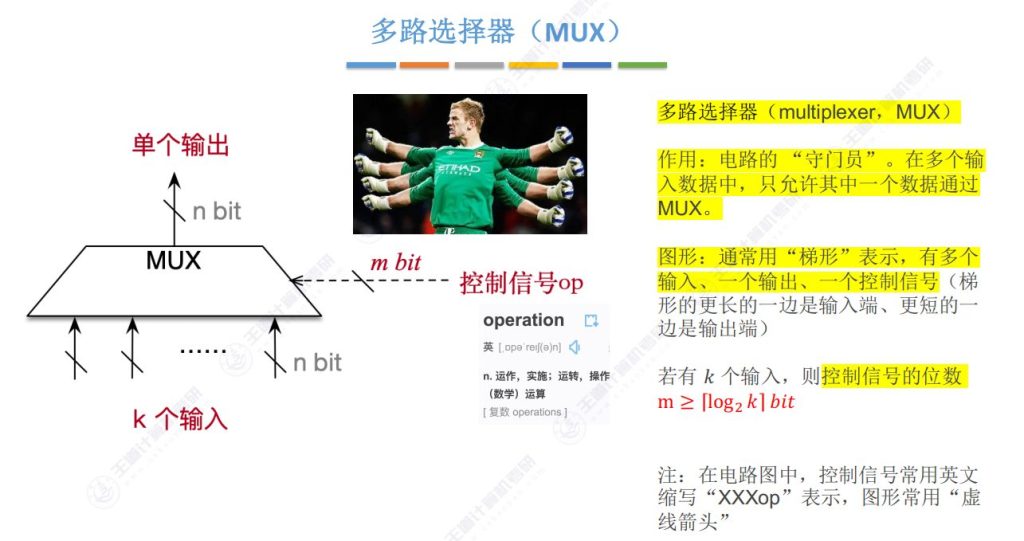
数据通常用实线表示、控制信号op用虚线表示
- 基本结构:包含多个输入(k个)、单个输出(n bit)和控制信号(m bit),英文缩写为MUX(Multiplexer)
- 工作原理:根据控制信号的值选择其中一个输入通过并输出,其他输入被阻断,类似”守门员”功能
- 图形表示:梯形符号表示,宽边为输入端,窄边为输出端,控制信号用虚线箭头标注在梯形腰部
- 控制信号位数:当有k个输入时,控制信号位数m⩾⌈log2k⌉bit(例如8个输入需要3位控制信号)
- 信号表示:控制信号常用”op”表示(operation缩写),数据信号用实线表示,控制信号多用虚线表示
2.2 多路选择器例子
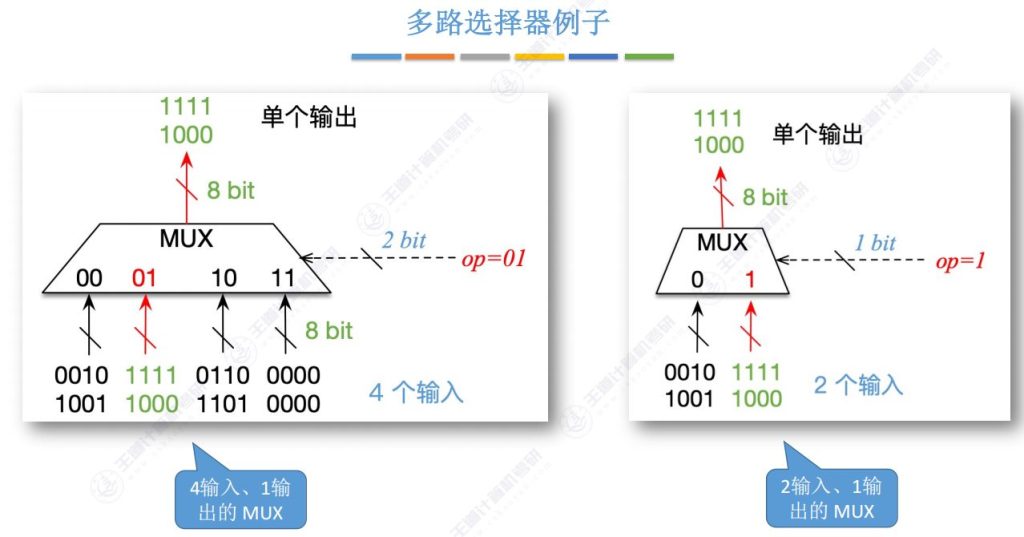
- 四输入MUX:
- 控制信号2位(00/01/10/11对应四个输入)
- 当op=01时选择第二个输入通过
- 二输入MUX:
- 控制信号1位(0/1对应两个输入)
- op=0选择左输入,op=1选择右输入
2.3 三态门
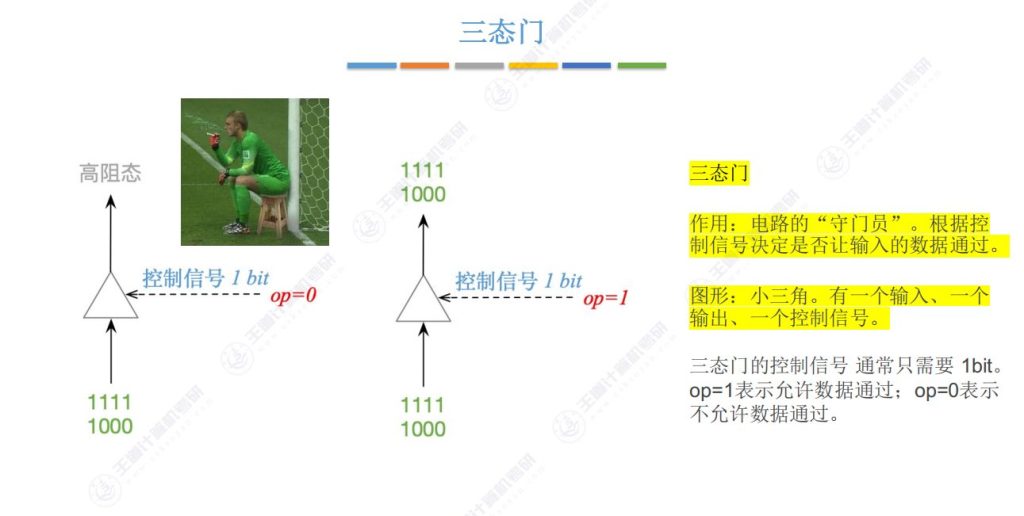
- 基本功能:单输入单输出的”守门员”,控制信号决定是否让输入通过
- 工作状态:
- 控制信号=1:输入直接通过
- 控制信号=0:输出高阻态(相当于断开线路)
- 图形表示:三角形符号,底边为输入,顶点为输出,腰部为控制信号端
高阻态
- 电平特性:既非高电平(如5V)也非低电平(如1V),实际表现为0V
- 电路效果:相当于物理断开连接线路,完全阻断信号传输

2.4 三态门vs非门
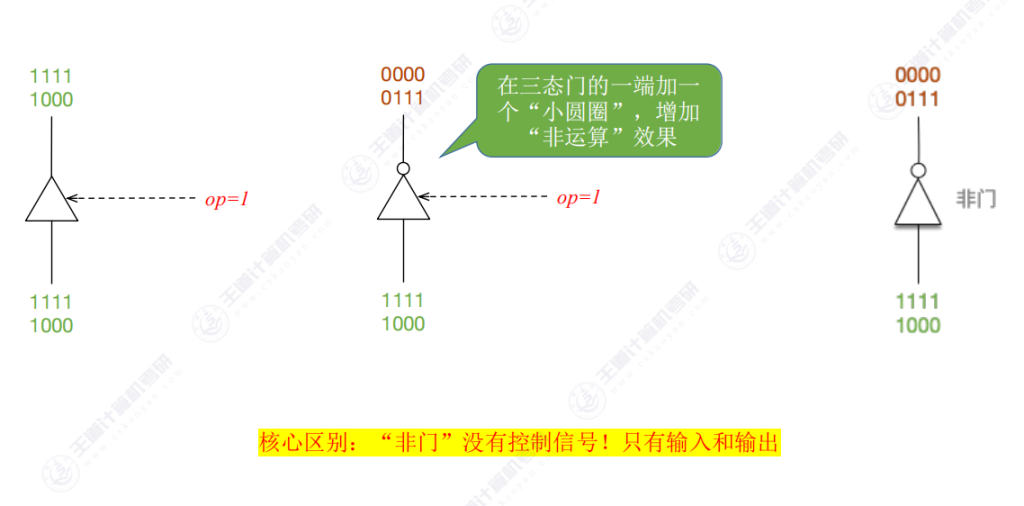
- 核心区别:
- 三态门有控制信号,可选择性阻断
- 非门无控制信号,必定通过并取反
- 变体形式:带圆圈的三态门会在通过时执行按位取反操作(1变0,0变1)
- 图形识别:需通过是否存在控制信号端来区分二者
2.5 内容总结
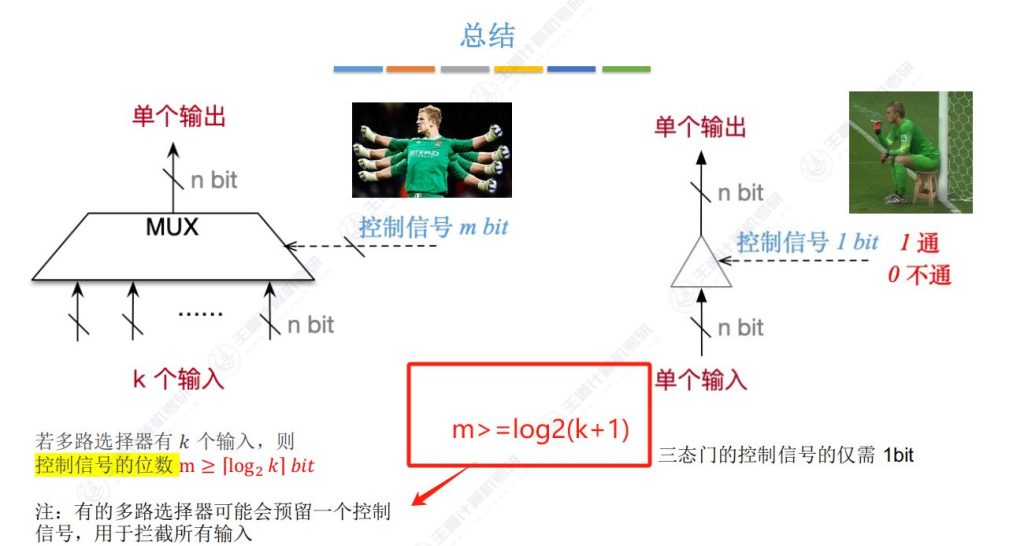
- 共同点:都作为数字电路中的信号控制部件
- 差异点:
- 多路选择器:多输入单输出,控制信号位数与输入数量相关
- 三态门:单输入单输出,控制信号仅需1位
注:有的多路选择器可能会预留一个控制信号,用于拦截所有输入

三、加法器

3.1 加法器的基本功能
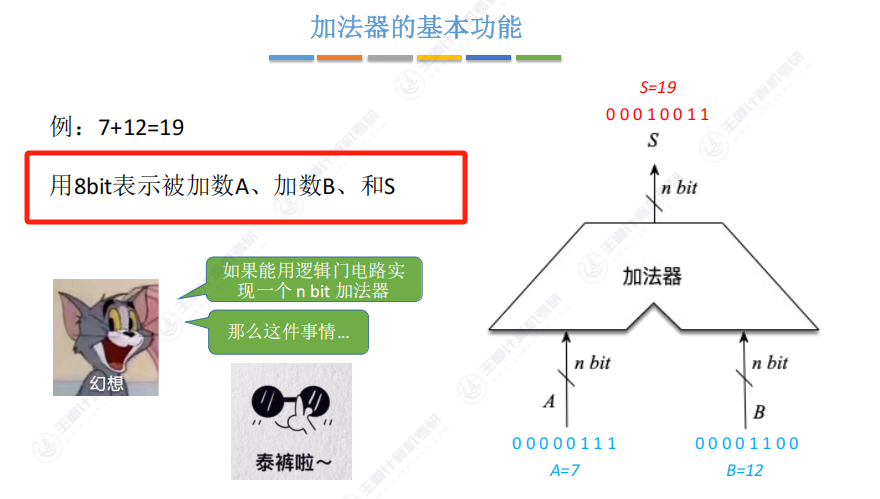
- 运算本质:实现两个n位二进制数的加法运算,如示例中A=7(00000111)2与B=12(00001100)2相加得到S=19(00010011)2
- 输入输出结构:
- 输入:被加数A和加数B各n位二进制数
- 输出:n位和的二进制结果
- 实现目标:用逻辑门电路构建n位加法器,完成二进制加法运算
3.2 一位的全加器(FA,full adder)
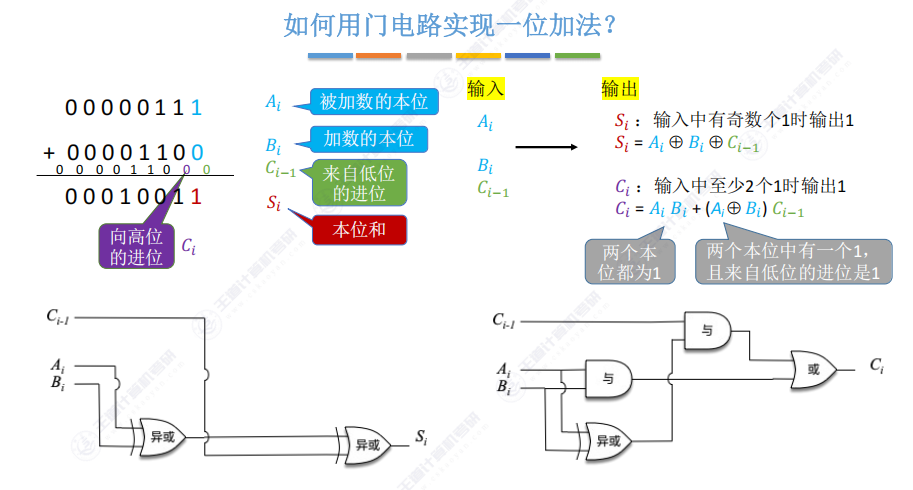
理解上述输出公式
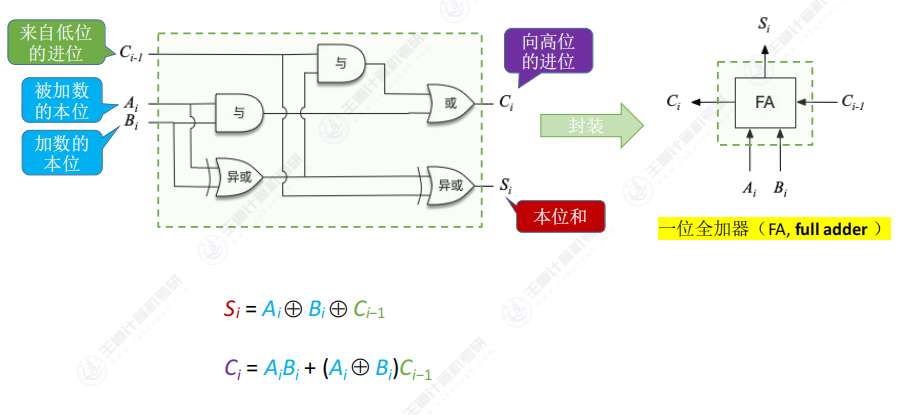
合并原理:将两个子电路集成
电路组成:
本位和电路:双异或门结构
进位电路:与门和或门组合实现
封装形式:隐藏内部电路细节,仅保留输入输出接口
英文缩写:FA(Full Adder)
功能说明:完成1位二进制数的全加运算(含进位处理)
3.3 n bit加法器
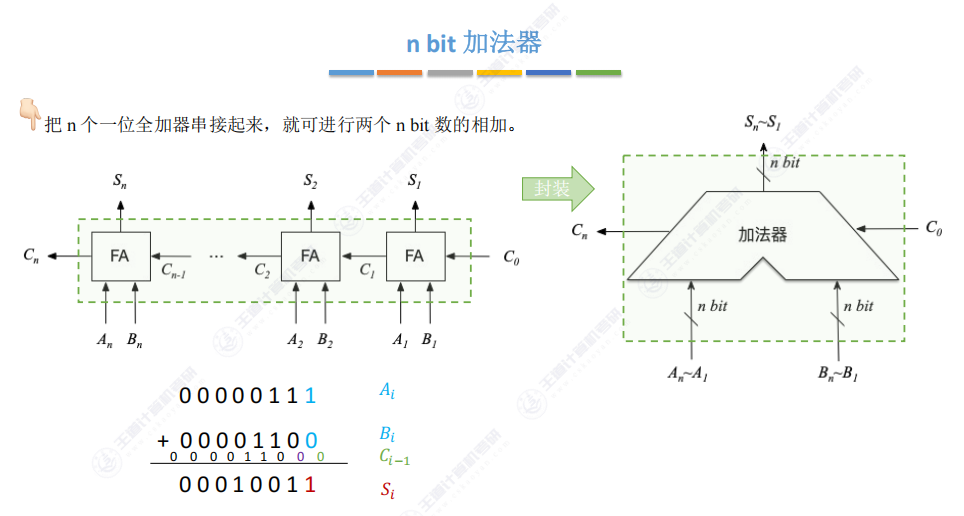
- 构建方法:将n个一位全加器串联连接
- 工作流程:
- 被加数和加数的各位并行输入对应FA
- 进位信号从低位向高位逐级传递
- 最终输出n位和结果
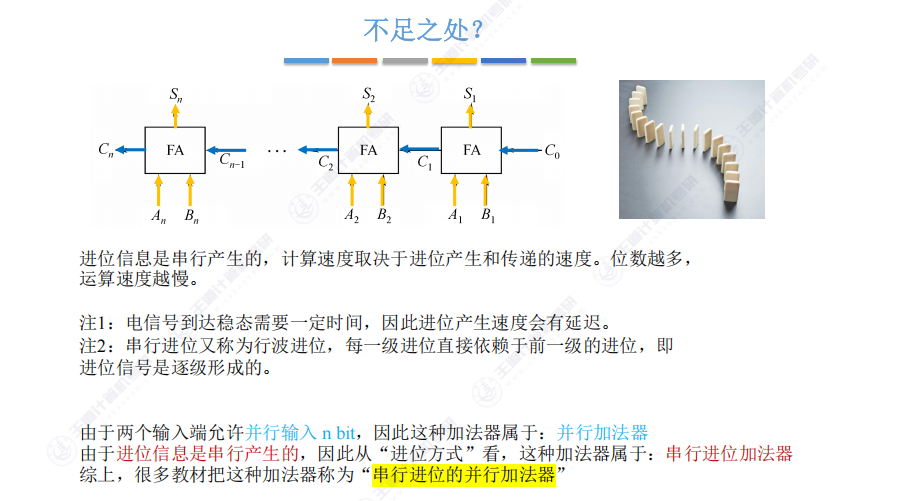
- 速度问题:
- 进位信息是串行产生的,计算速度取决于进位产生的速度和传递的速度。位数越多,运算速度越慢。这种串行进位信息又称为行波进位
- 并行加法器:支持n位数据并行输入但进位串行的结构(也称串行进位的并行加法器)
3.4 并行进位的并行加法器
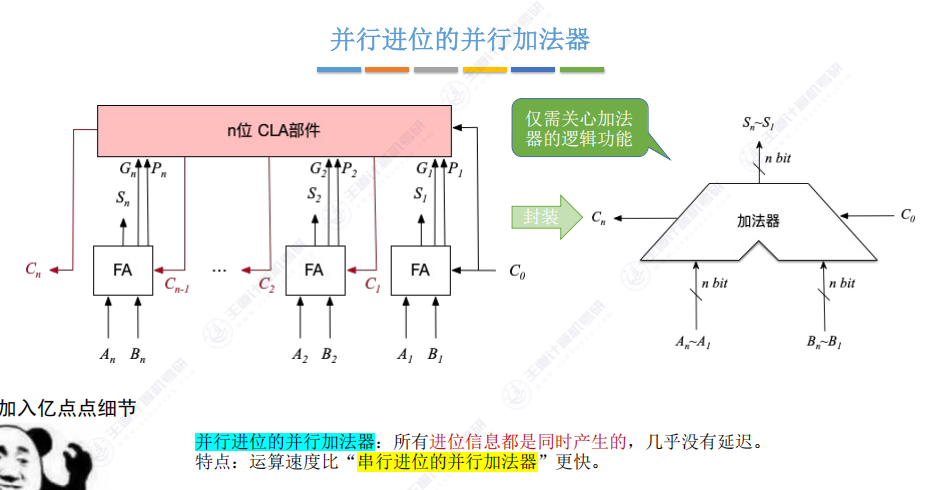
- 工作原理:通过增加CLA部件同时产生所有进位信息,实现进位并行处理
- 核心优势:相比串行进位加法器,运算速度显著提升
- 特点:
- 所有进位信息同时产生
- 进位延迟几乎为零
- 封装后与串行进位加法器图示相同
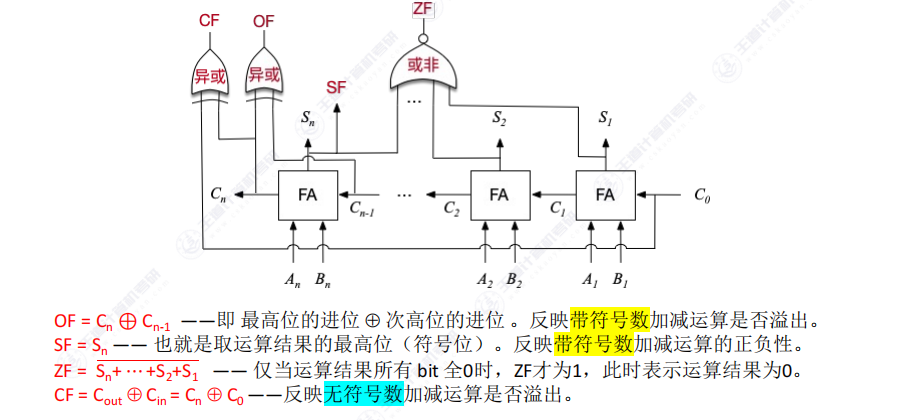
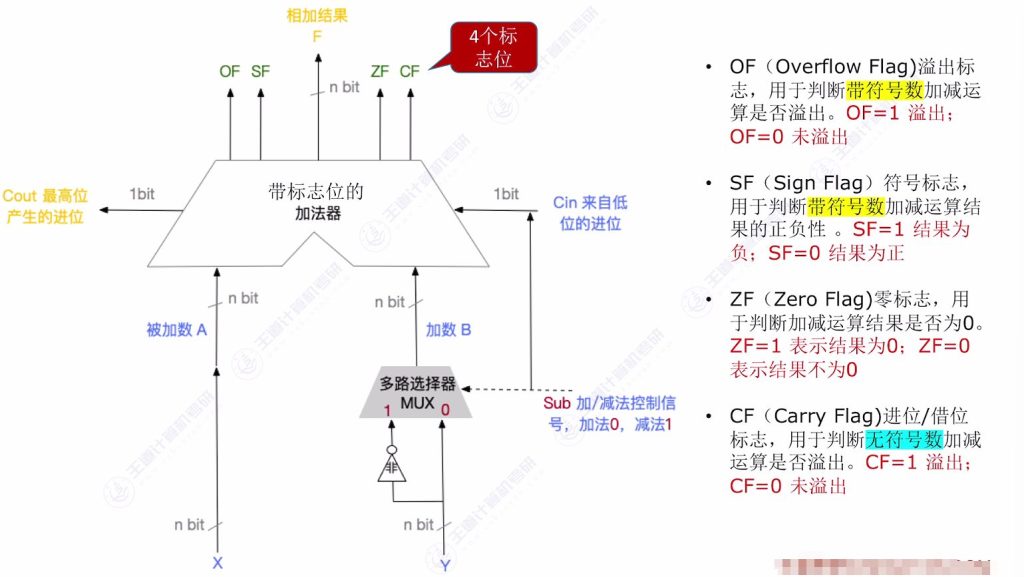
3.5 带标志位的加法器
设计目的:解决加法运算结果判断问题
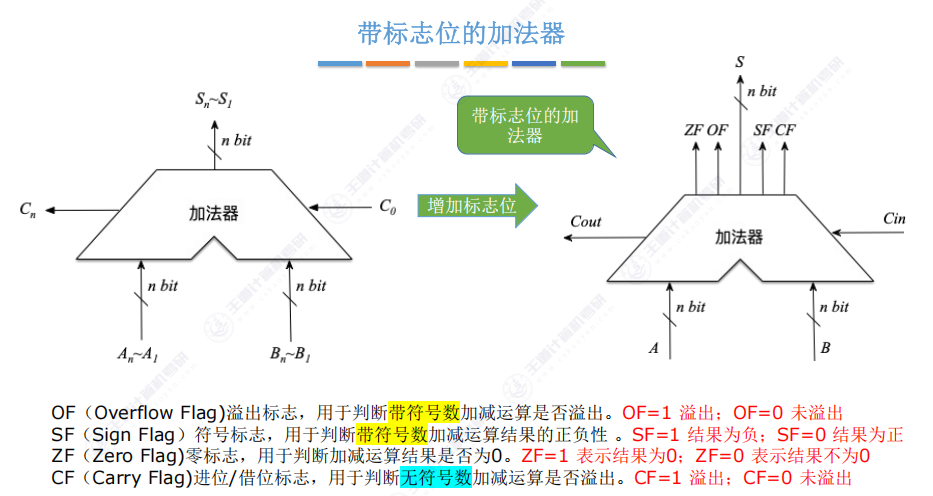
- 判断结果是否溢出(n位表示范围限制)
- 判断结果是否为零(用于相等性比较)
- 判断结果正负(用于大小比较)
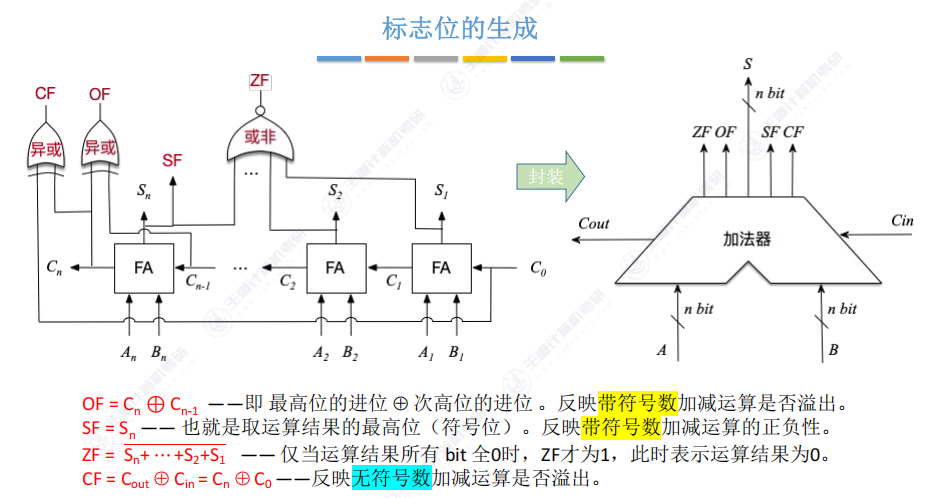
- OF(溢出标志)Overflow Flag

- SF(符号标志)Sign Flag-直接取最高位

- ZF(零标志)Zero Flag(无论是有符号还是无符号)

- CF(进位标志)Carry Flag(用于无符号)

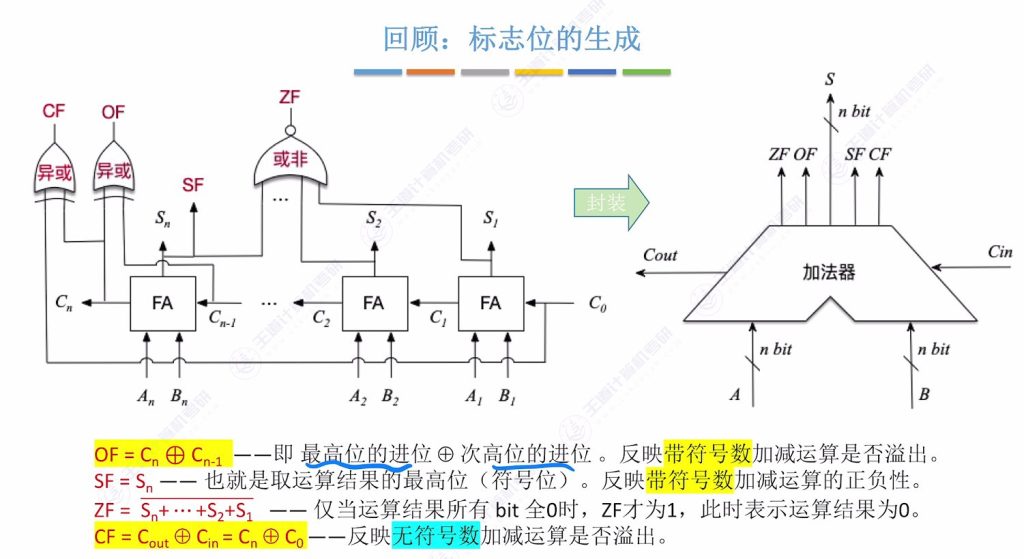
3.6 知识回顾
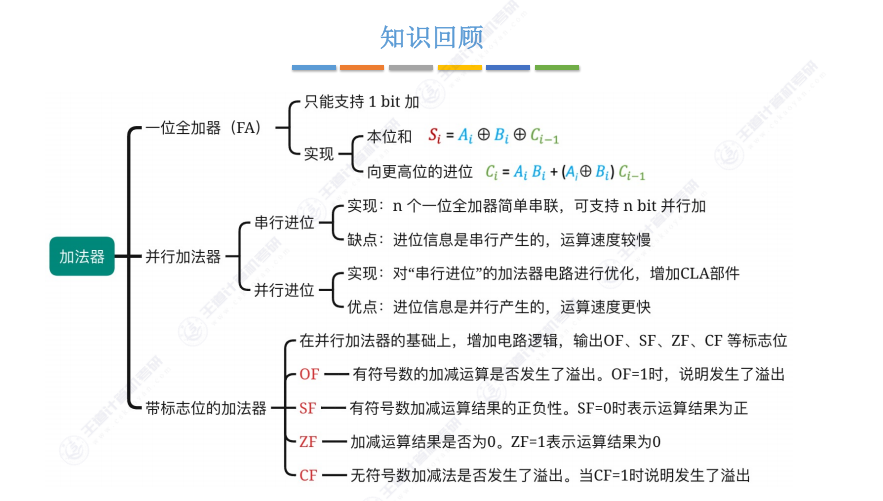
ZF 对有符号、无符号均成立
3.7 补充8bit无符号数和有符号数表示范围

3.8 用例子理解 Carry Flag 的作用
CF 标志与溢出的关系
CF(Carry Flag,进位 / 借位标志)直接反映 无符号数运算是否溢出:
CF=1:表示运算产生了进位(加法)或借位(减法),结果超出无符号数范围 → 溢出。CF=0:表示无进位 / 借位,结果在无符号数范围内 → 未溢出。
题目公式的简化理解
→ 无符号数运算时,看 CF 标志:1 是溢出,0 是没溢出。
举个例子:
- 8 位无符号数
255 + 1:加法后最高位进位,CF=1→ 溢出(结果应为 256,超出 8 位无符号范围)。 - 8 位无符号数
100 + 50:结果 150,无进位,CF=0→ 未溢出。
四、算术逻辑单元ALU
学习目标:理解ALU在计算机中的作用、功能、实现原理及图示解读方法
重点掌握:ALU的功能分类、控制信号位数计算、标志位信息
简要了解:ALU的电路实现原理(非考试重点)
4.1 ALU = Arithmetic and Logic Unit 算术逻辑单元的作用
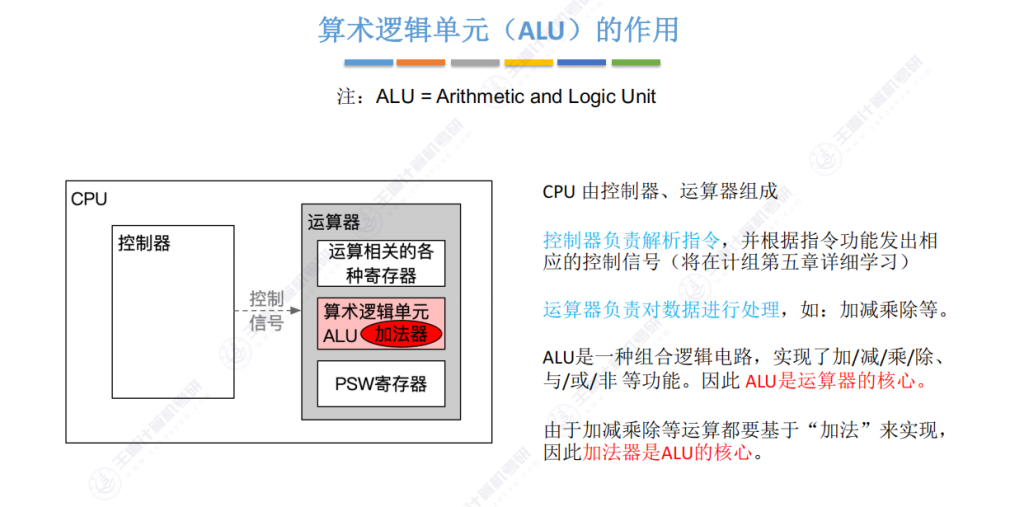
- 核心地位:ALU是运算器的核心部件,而运算器与控制器共同组成CPU,加法器又是ALU的核心
- 工作流程:
- 控制器:解析指令并发出控制信号(包括发给运算器的信号)
- 运算器:根据控制信号处理数据(通过ALU执行具体运算)
- 组成关系:CPU→运算器→ALU→加法器(核心中的核心)
- 运算器组成:
- 通用寄存器组:存储参与运算的数据
- ALU:实现算术/逻辑运算的组合逻辑电路
- PSW寄存器:存储CPU状态和运算状态信息
- 设计原理:所有运算(加减乘除)最终都基于加法实现
4.2 ALU的功能
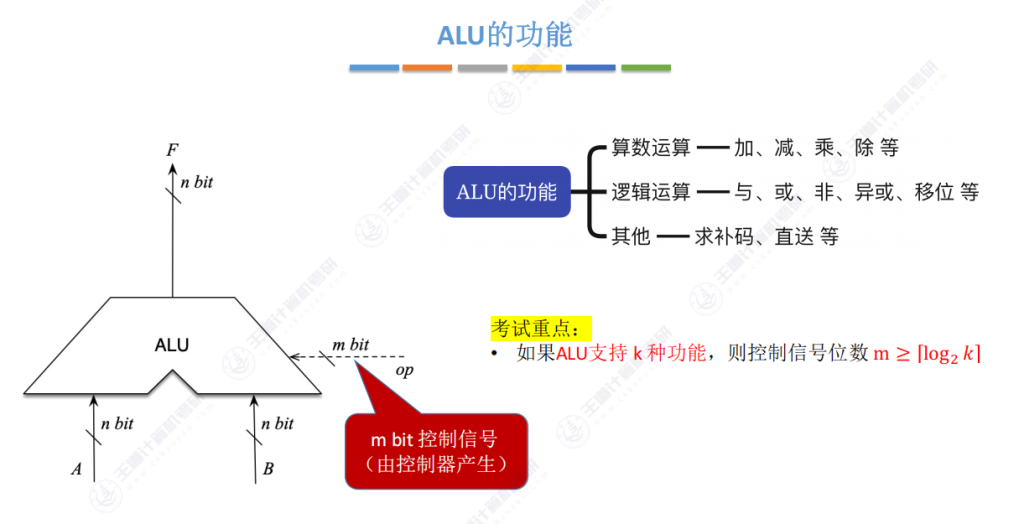
重点
- 图中ALU 11种功能,则需要4bit
功能说明:
求补码:将原码输入后输出对应补码,便于硬件实现加减运算
直送功能:数据不经处理直接输出(如输入0001则输出0001)
4.3 ALU的实现原理(最简单的模型)了解即可
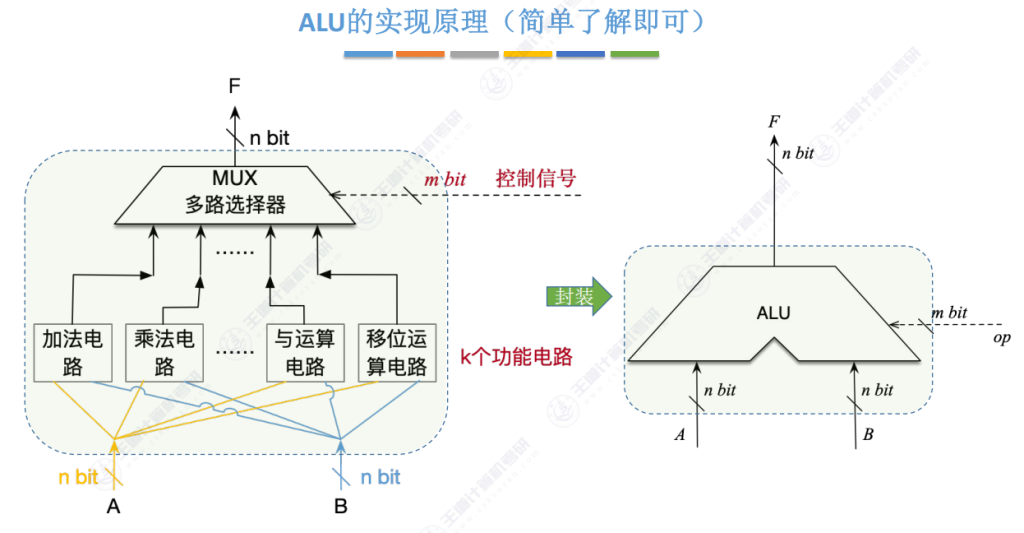
- 基础实现方案:
- 并行设置多个功能电路(加法、乘法、与运算等)
- 通过多路选择器(MUX)选择输出结果
- 控制信号决定MUX的输出线路
- 示例说明:
- 2位控制信号可管理4种功能(00→加法,01→乘法等)
- 封装后形成完整ALU模块
4.4 看懂AUL图示(超级重点)
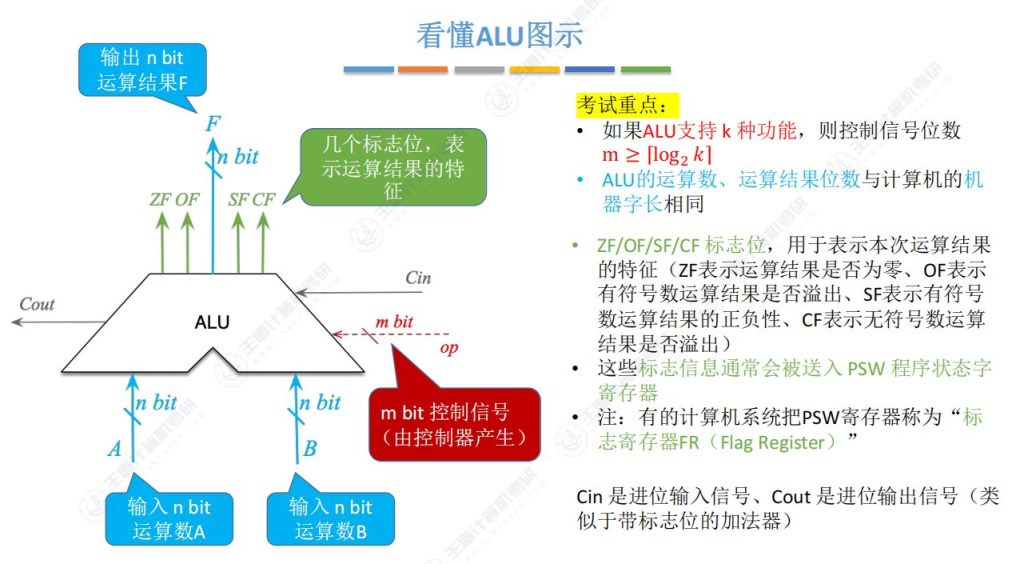
ALU的运算数、运算结果位数与计算机的机器字长相同,可以说,ALU的运算数决定机器字长
PSW和FR是一个东西两个名字
4.5 ALU真题演练
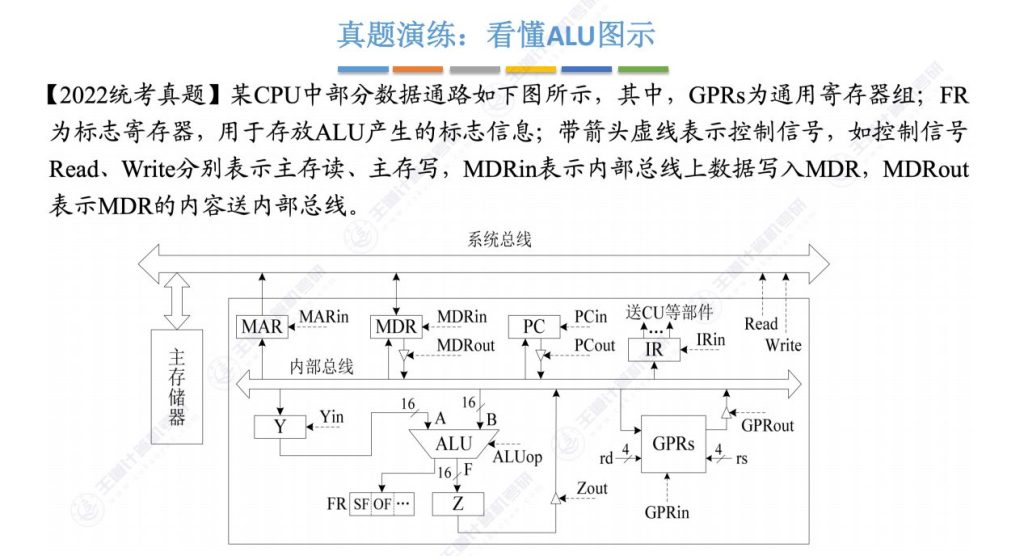
- 关键观察点:
- ALU输入/输出位数(图示中为16位)
- 控制信号来源(ALUop来自控制器)
- 标志位输出(连接FR寄存器)

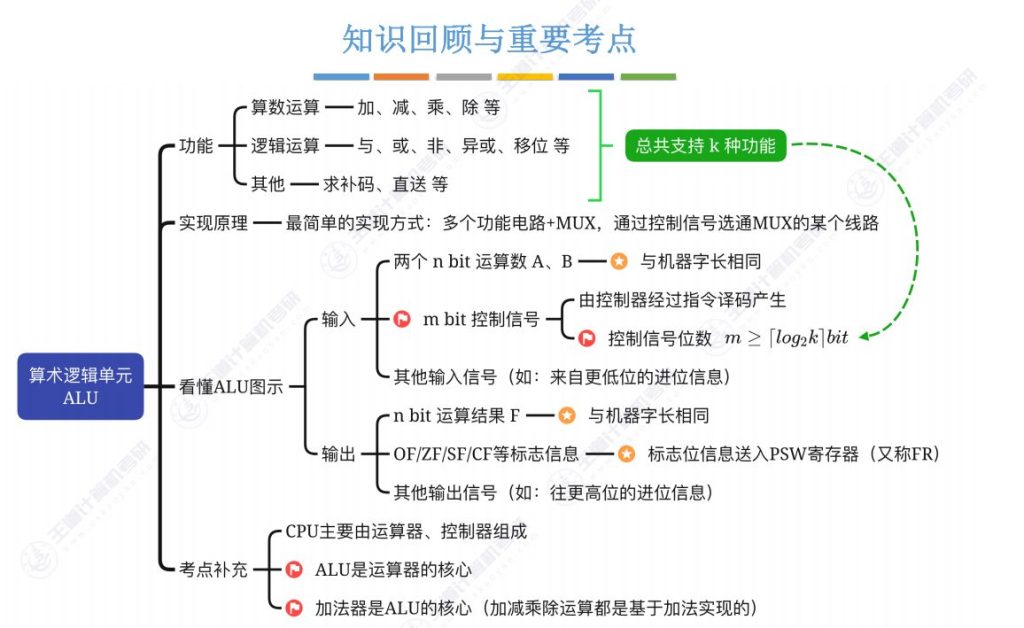
4.6 知识回顾
五、定点数的移位运算
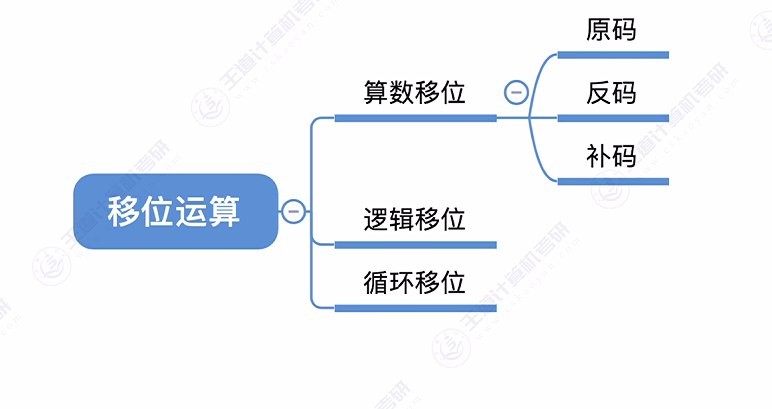
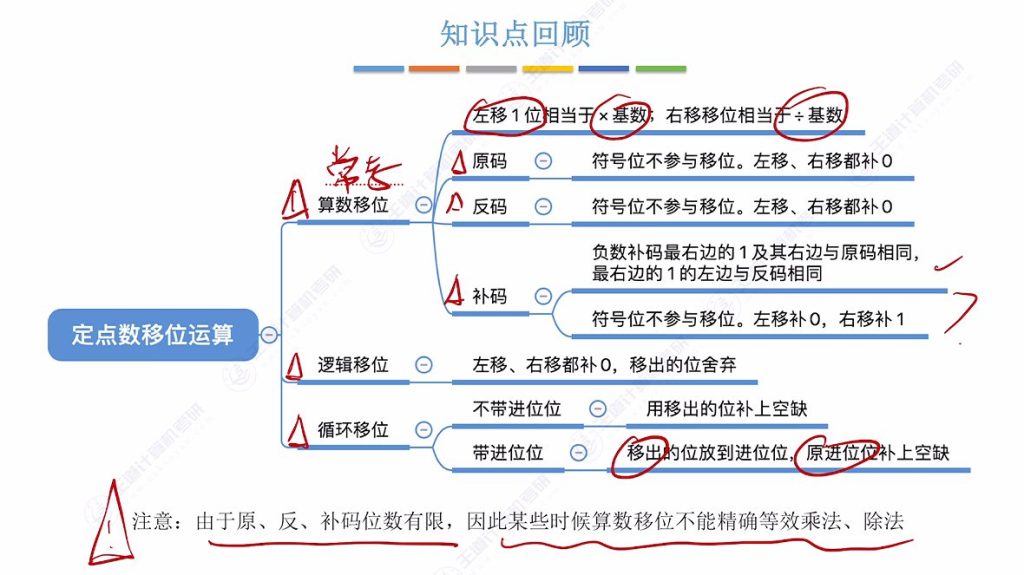
分类:定点数移位运算分为算术移位、逻辑移位和循环移位三种类型
5.1 算数移位 – 十进制数小数点移位

- 基本原理:通过改变数码位与小数点的相对位置来改变位权
- 右移效果:小数点后移1位相当于×101×10^1×101,如9852.11→98521.1
- 左移效果:小数点前移1位相当于÷101÷10^1÷101,如985.211→98.5211
- 本质:算术移位可等价实现乘除法运算
5.2 原码的算数移位 – 左移、右移
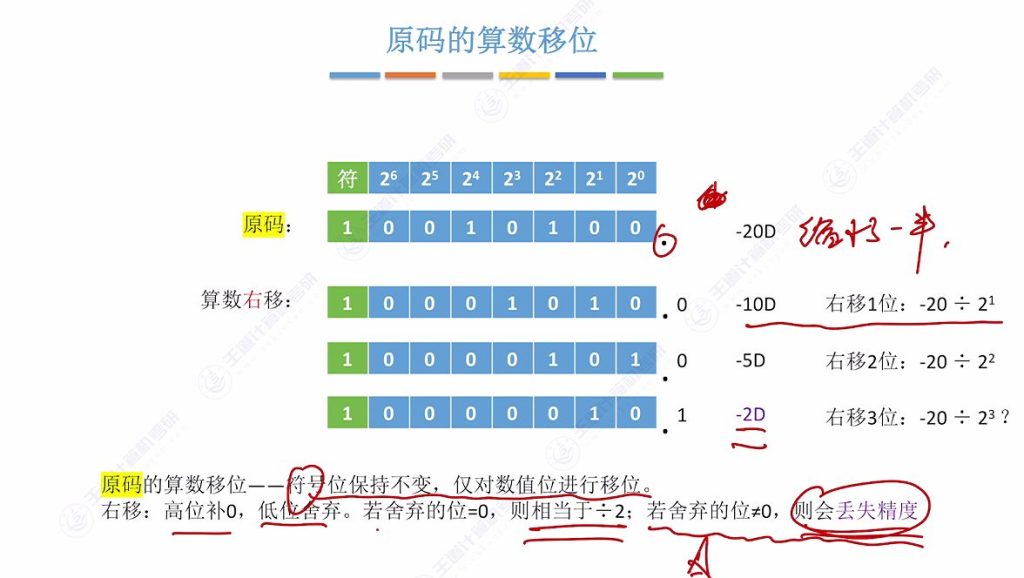
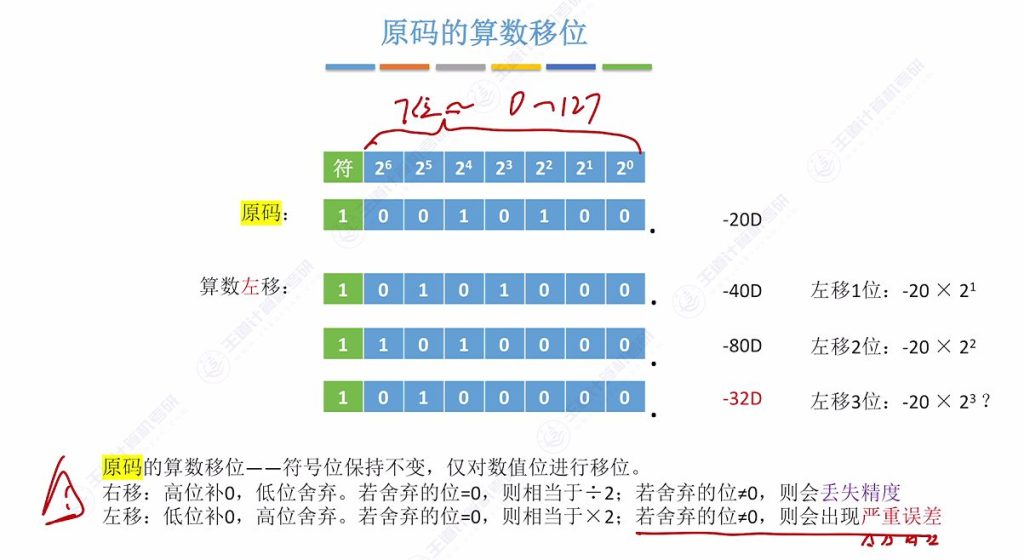
- 规则:符号位保持不变,仅对数值位进行移位
- 右移操作:
- 方法:高位补0,低位舍弃
- 效果:相当于÷2(舍弃位为0时精确)
- 示例:-20D右移1位得-10D(−20÷21)
- 精度问题:若舍弃位≠0会丢失精度(如-5D右移1位得-2D而非-2.5D)
- 左移操作:
- 方法:低位补0,高位舍弃
- 效果:相当于×2×(舍弃位为0时精确)
- 溢出问题:若舍弃位≠0会出现严重误差(如-40D左移3位得-32D而非-160D)
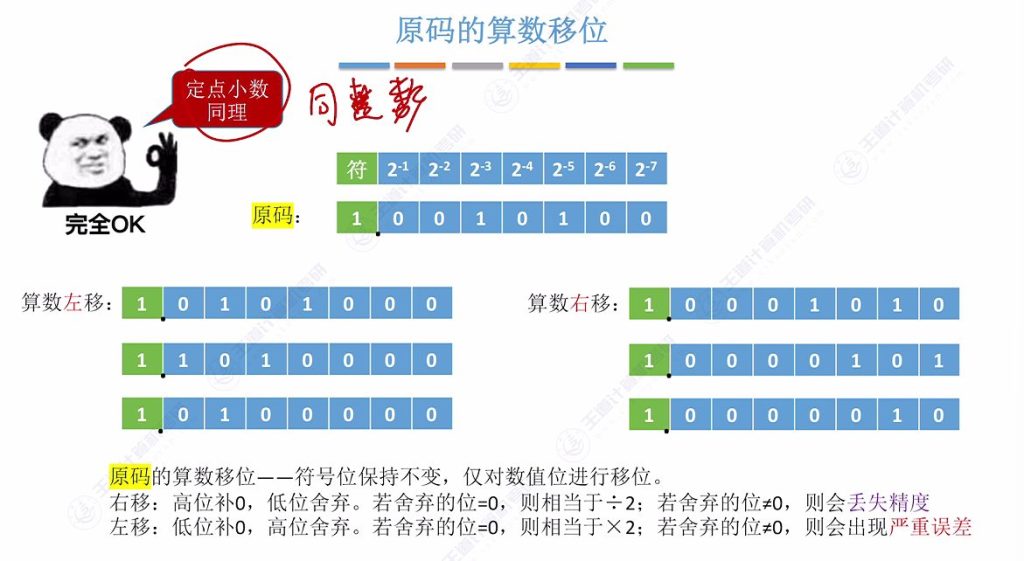
定点小数同整数算数位移结论一致
5.3 反码的算数移位
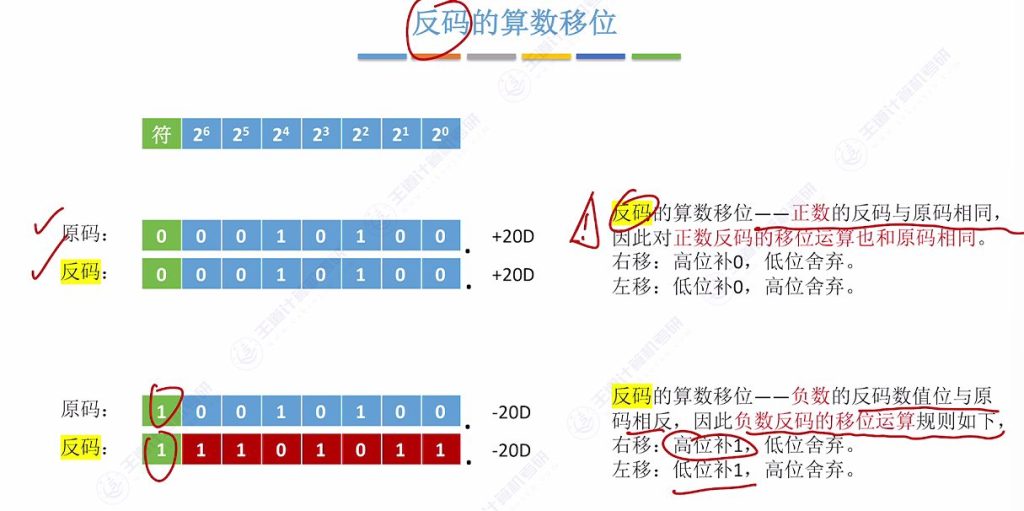
- 正数处理:与原码完全相同(左/右移均补0)
- 负数处理:
- 补位规则:无论左移右移都补1
- 原因:负数反码的数值位与原码相反
5.4 补码的算数移位
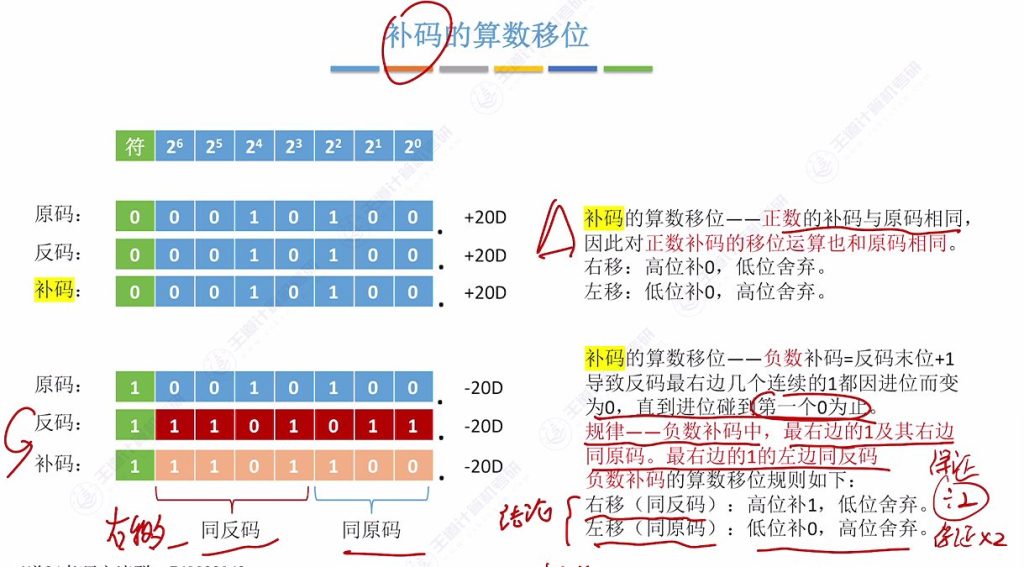
- 正数处理:与原码完全相同(左/右移均补0)
- 负数处理:
- 右移:高位补1,低位舍弃
- 左移:低位补0,高位舍弃
- 原理:补码最右边的1及其右侧与原码相同,左侧与反码相同
5.5 算数移位总结
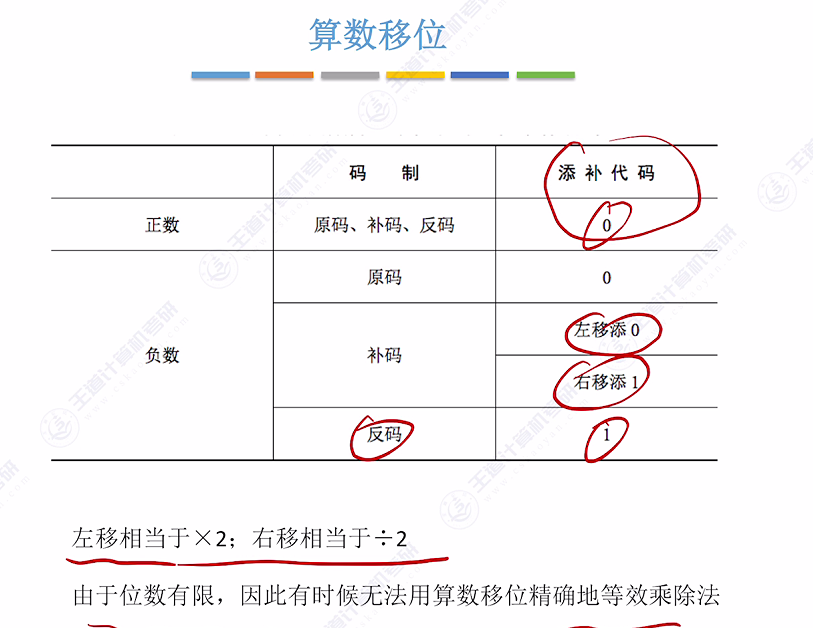
- 正数统一:原码/反码/补码均补0
- 负数差异:
- 原码:左右移均补0
- 反码:左右移均补1
- 补码:左移补0,右移补1
- 运算效果:左移相当于×2,右移相当于÷2
5.6 算数移位的应用举例
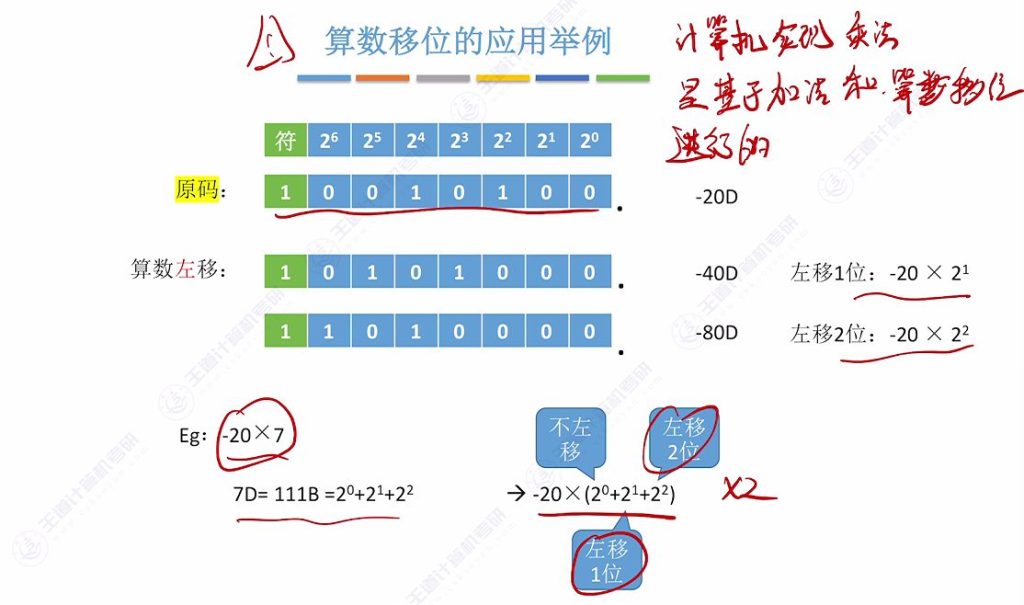
- 硬件实现:通过移位和加法组合实现乘法
5.7 逻辑移位

- 规则:
- 右移:高位补0,低位舍弃
- 左移:低位补0,高位舍弃
- 本质:可看作无符号数的算术移位
5.8 逻辑移位的应用案例
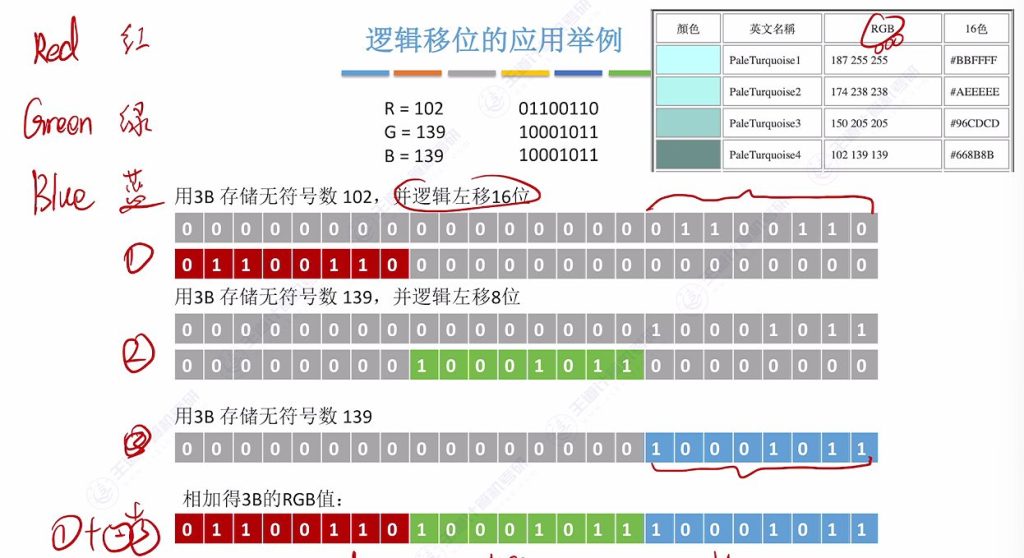
- 应用场景:RGB颜色值的存储组合
- 实现方法:
- 将R值(102)逻辑左移16位
- 将G值(139)逻辑左移8位
- 将B值(139)保持不变
- 三者相加得到24位RGB值
5.9 循环移位
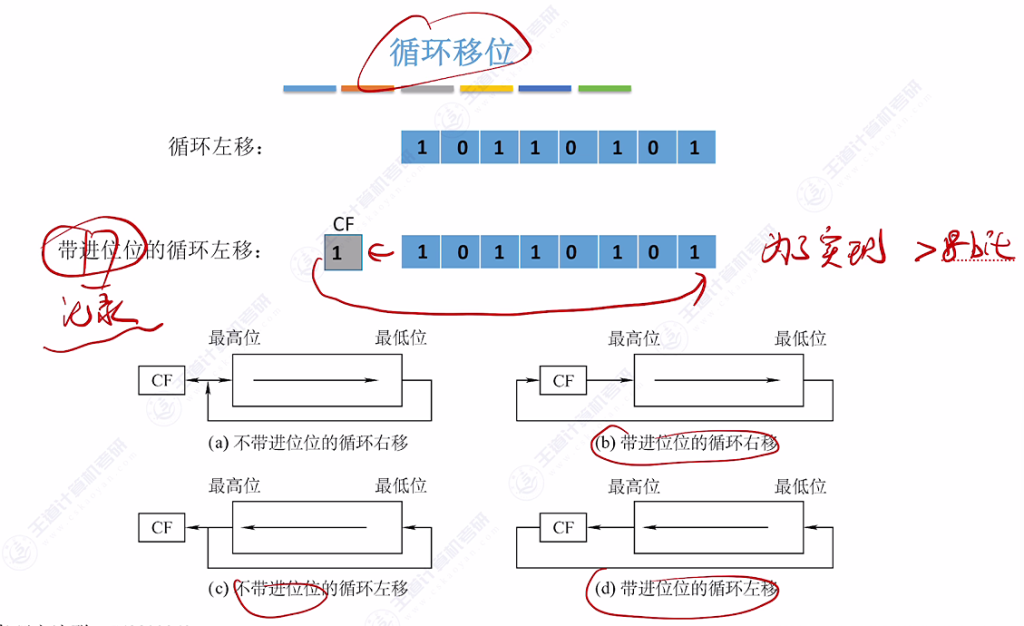
- 基本循环移位:
- 移出的位填补到空缺位
- 形成循环效果
- 带进位位循环移位:
- 移出位存入进位位(CF)
- 原进位位填补空缺位
- 适用于多字节运算
5.10 知识点回顾
六、补码加减运算电路
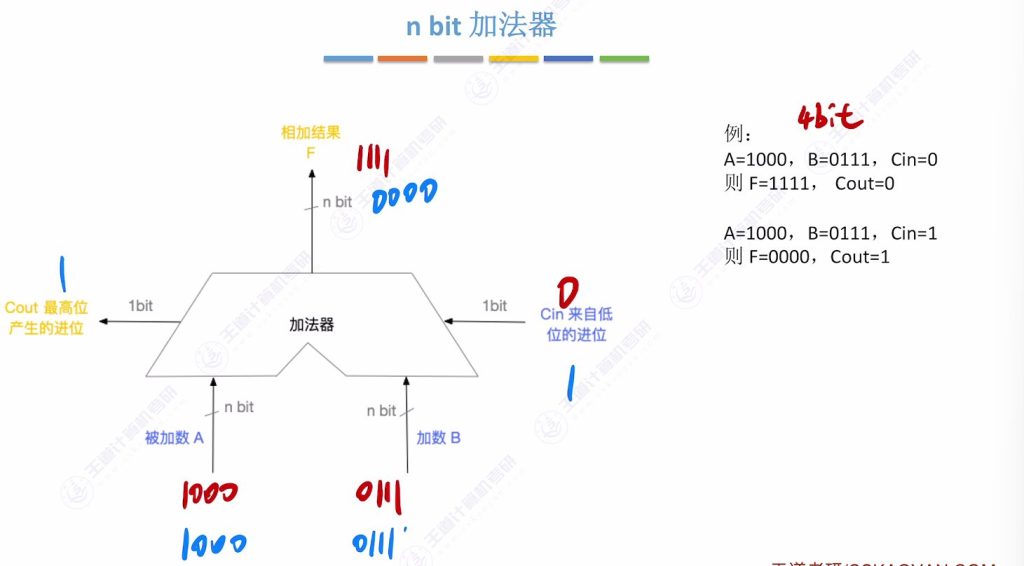
6.1 n bit 加法器
6.2 补码加减运算电路
有符号数的加减运算
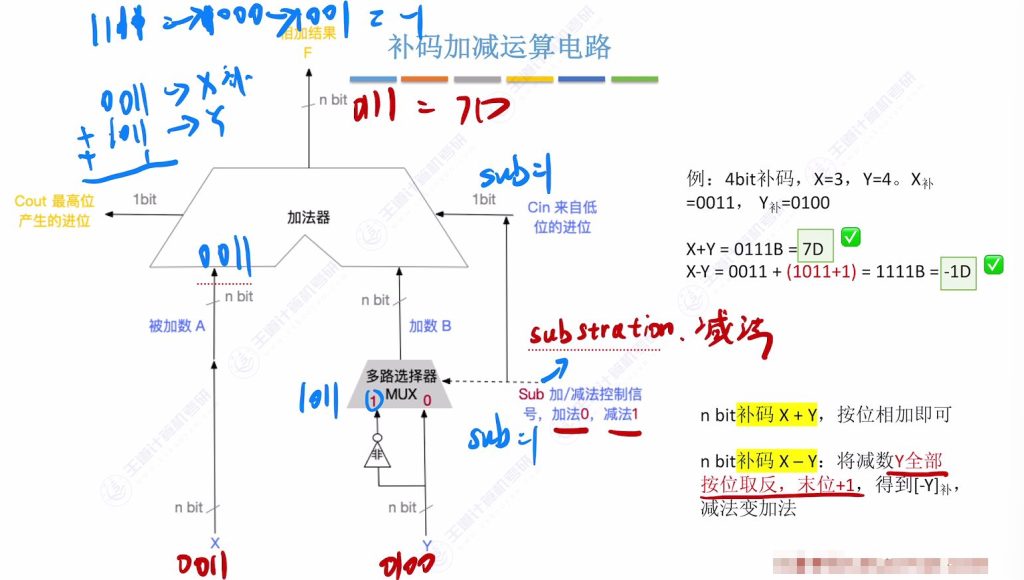
减法运算也可以用加法器实现:
对于减法:减数全部按位取反
无符号数的加减运算
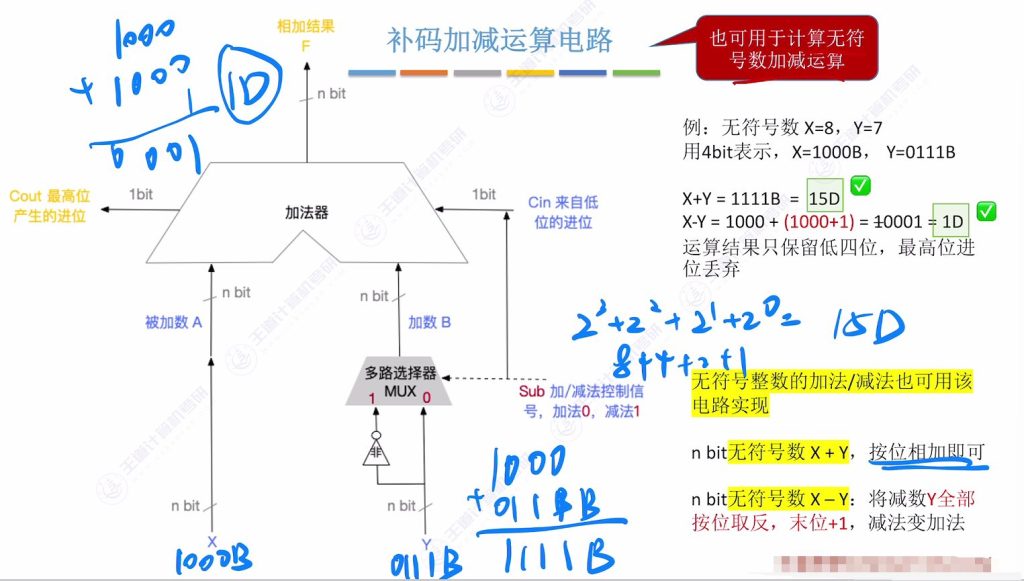
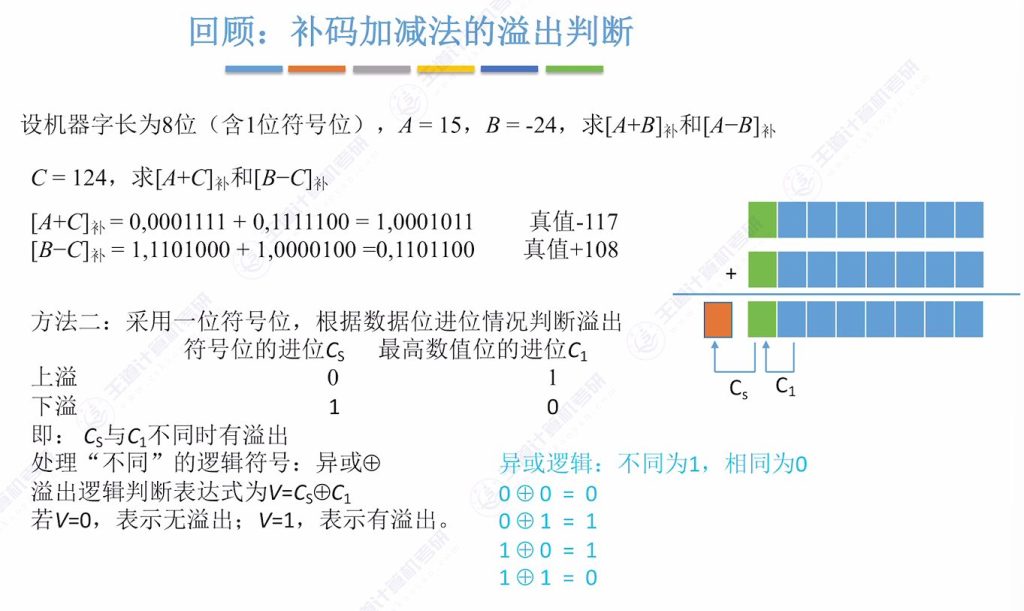
6.3 补码加减法的溢出判断

七、定点数原码的乘法运算(重点)
7.1 乘法运算的思想(十进制)

- 小数点处理:从结果最右端向左数6位(被乘数3位+乘数3位)确定小数点位置。
7.2 乘法运算的思想(二进制)

- 确定小数点位置的方法:被乘数小数位数(4位)加乘数小数位数(4位)等于结果小数位数(8位)
- 位积特性:二进制每位只有0或1,位积要么是被乘数本身,要么是全零。
硬件优势:仅需判断0/1决定是否累加,配合移位寄存器即可实现。
效率对比:相比十进制乘法,二进制无需乘法口诀表,硬件电路更简单。
7.3 机器实现几个问题
1、实际数字有正负,符号位如何处理?
答:符号处理用位异或运算。符号位单独计算,数值部分按无符号数处理。
2、乘积的位数扩大一倍,如何处理?
如:5位数相乘可能产生9位结果,超出寄存器容量。
处理方法:采用双字长存储或动态调整数据表示范围。ACC 和 MQ
3、4个位积都要保存下来最后统一相加?
答:采用累加器逐步相加替代全部存储,通过”加-移位”操作减少寄存器使用。

所有位积的加权求和可通过累加过程中的循环右移操作完成。
7.4 原码的一位乘法
符号位异或单独处理
数值位取绝对值进行乘法计算

7.5 回顾运算器的基本组成
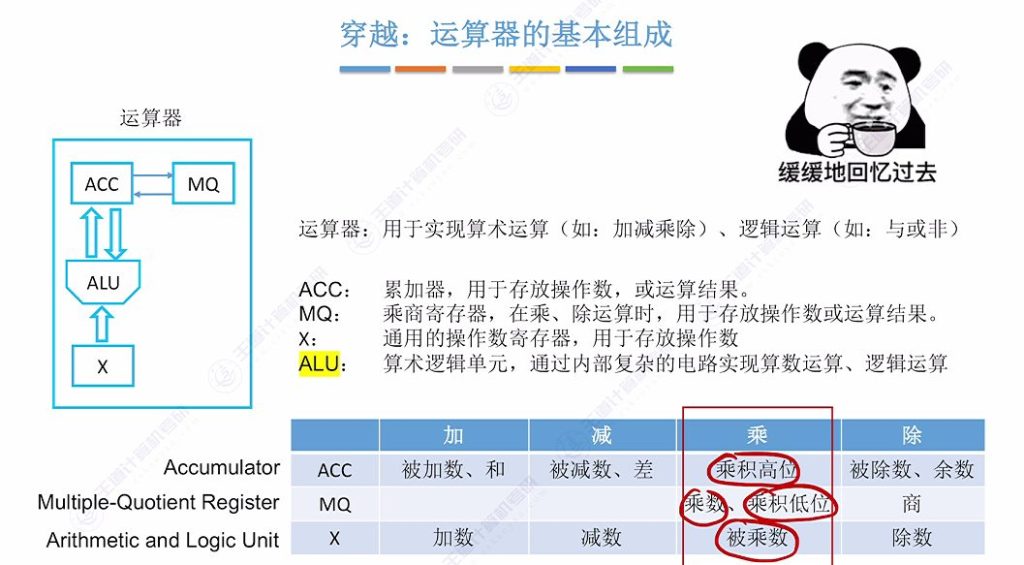
- ACC:累加器,存放操作数或运算结果。乘法时存放乘积高位。
- MQ:乘商寄存器,乘除运算时存放操作数或结果。乘法时存放乘数和乘积低位。
- X:通用操作数寄存器,存放被乘数。
- ALU:算术逻辑单元,实现算术和逻辑运算。
7.6 原码一位乘法实现案例
实现方法:先加法:(ACC)+(X) ->ACC,再逻辑右移,重复n次,这里的n指的是机器字长-1,1代表符号位
初始阶段
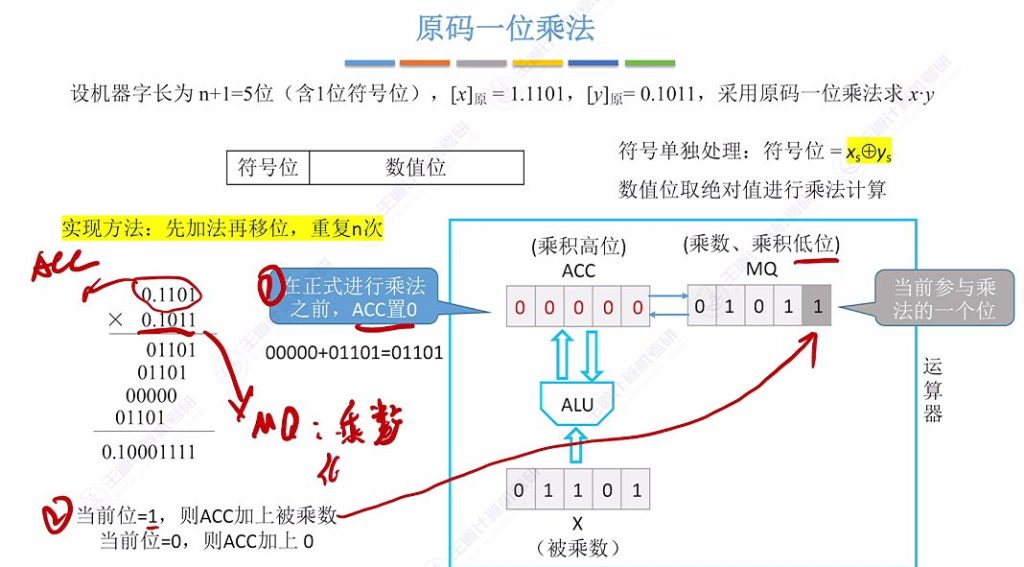
遇到当前位为 1 的情况:(ACC)+(X) ->ACC,之后逻辑右移
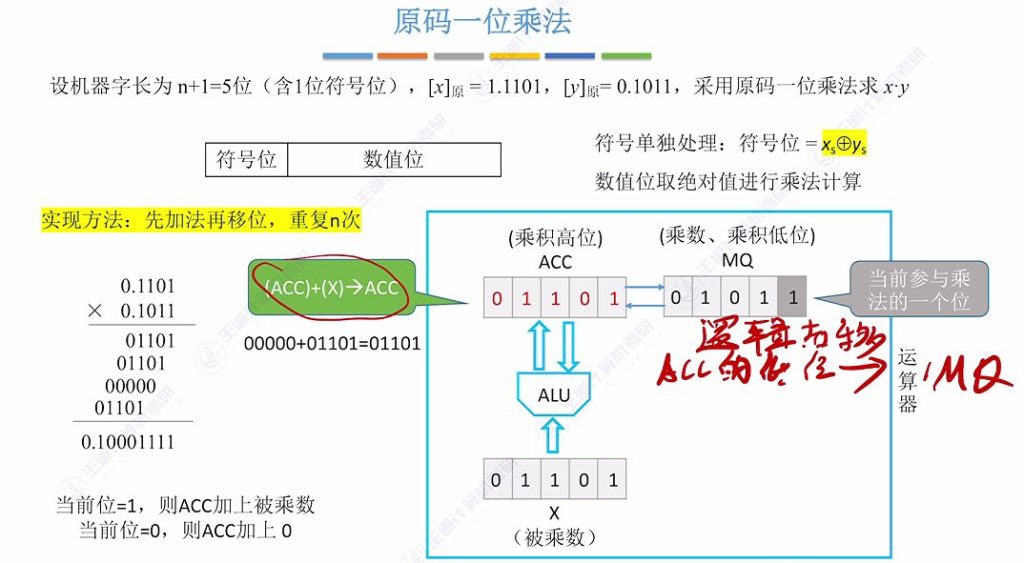
遇到当前为 0 的情况 (ACC)+(0) ->ACC,逻辑右移,重复n(数值位)次
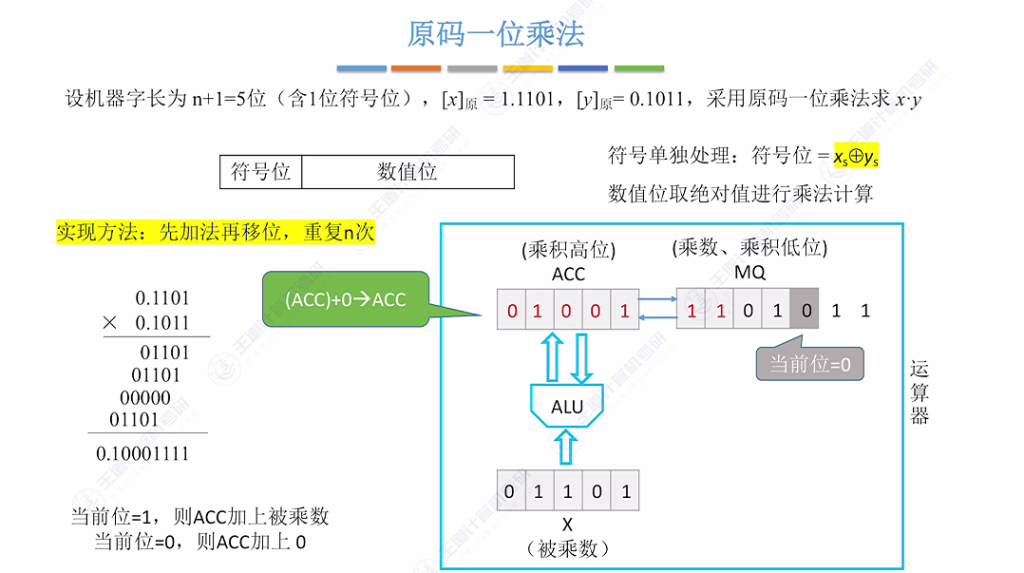
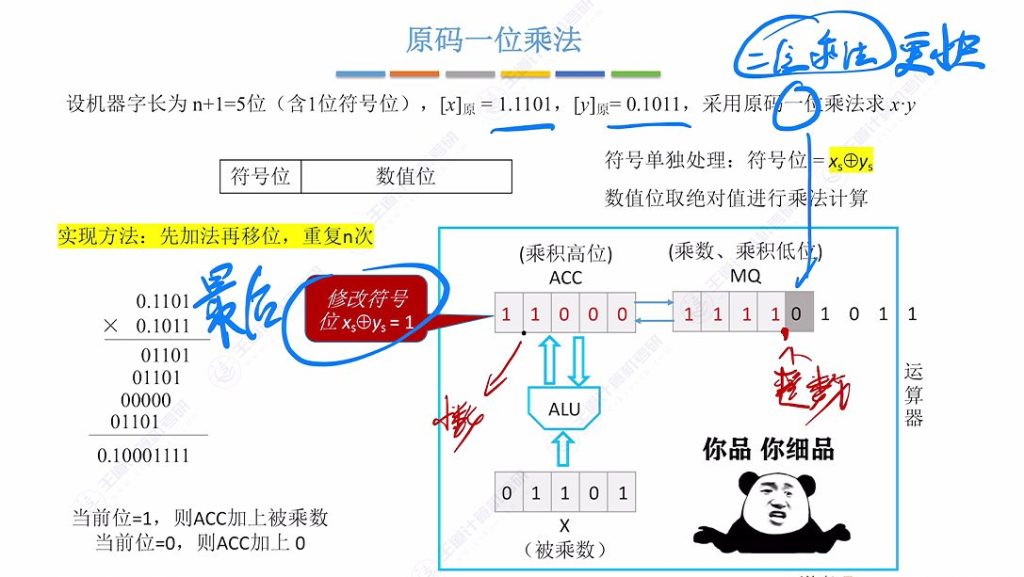
最终结果:
- 运算步骤:
- 检查MQ最低位:为1则ACC加被乘数,为0则加0
- 每次加法后,ACC和MQ整体逻辑右移1位(高位补0)
- 重复n次(n为数值位位数)
- 注意事项:
- 乘数符号位不参与运算
- 可使用单符号位或双符号位
- 最终结果应表示为原码机器数
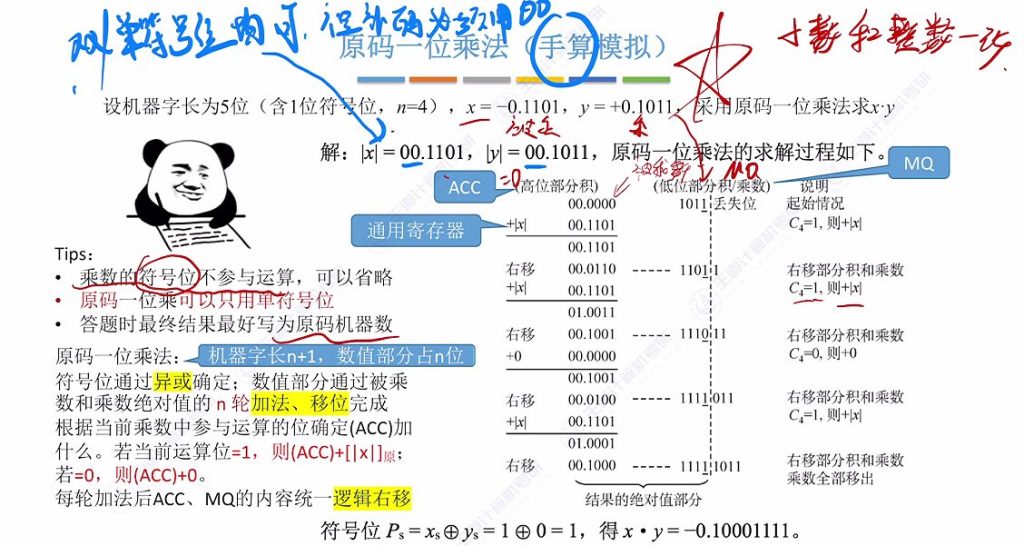
- 实例演示:
- 初始:ACC=00.0000,MQ=01011,X=00.1101
- 第1轮:MQ末位1→ACC+X=00.1101→右移得00.0110 1011
- 第2轮:MQ末位1→ACC+X=01.0011→右移得00.1001 1101
- 第3轮:MQ末位0→ACC+0=00.1001→右移得00.0100 1110
- 第4轮:MQ末位1→ACC+X=01.0001→右移得00.1000 1111
- 结果处理:
- 绝对值结果:0.10001111
- 符号位:1⊕0=1
- 最终结果:[x⋅y]原=1.10001111
- 整数与小数区别:
- 小数:小数点固定在符号位后
- 整数:小数点固定在数值位最后
- 运算过程完全相同
7.7 原码一位乘法(手算模拟)
八、定点数补码乘法运算
8.1 补码一位乘法
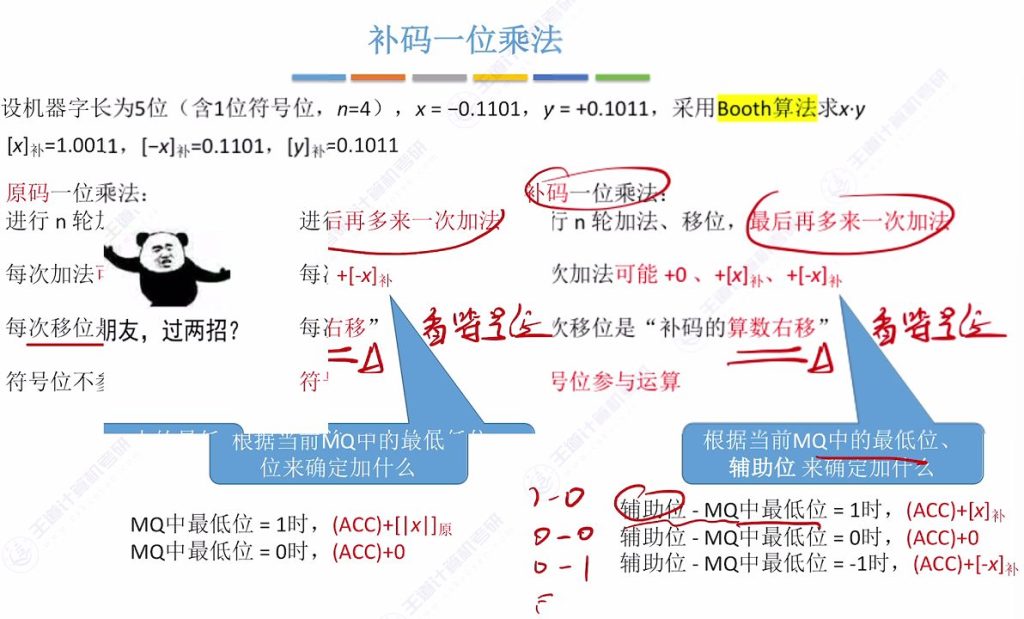
补码一位乘法与原码一位乘法的区别
- 加法操作差异:
- 原码每次加法可能+0或+[|x|]原[|x|]_原[|x|]原,由MQ最低位决定
- 补码每次加法可能+0、+[x]补或+[−x],由辅助位减去“MQ最低位”决定(结果为1/0/-1对应不同操作)
- 移位方式差异:
- 原码采用逻辑右移(高位补0)
- 补码采用算术右移(符号位不变,高位补符号位)
- 符号位处理:
- 原码符号位单独异或确定,不参与运算
- 补码符号位直接参与运算,结果自然体现符号
8.2 补码一位乘法的硬件构成
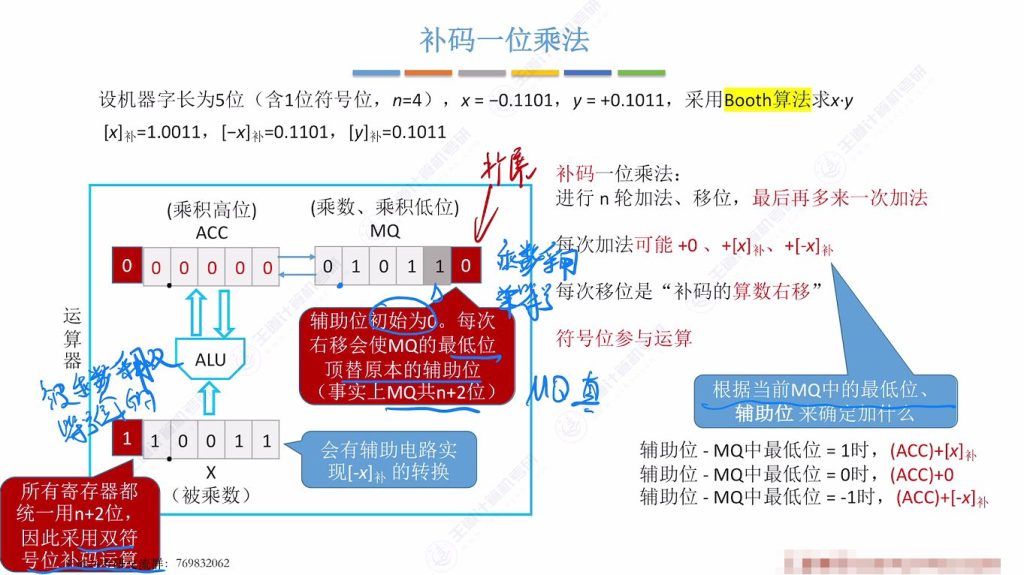
- 寄存器扩展:
- MQ寄存器扩展1位作为辅助位(共n+2位)
- ACC和X寄存器同步扩展为双符号位
- 数据存储规则:
- 被乘数存储双符号位补码
- 乘数存储单符号位补码(因MQ需保留辅助位)
- 辅助电路:
- 专用电路实现x补码到−x补码的快速转换
- 移位机制:
- 每次右移使MQ原最低位顶替辅助位
- 算术右移时符号位保持不变
8.3 补码一位乘法(手算模拟)
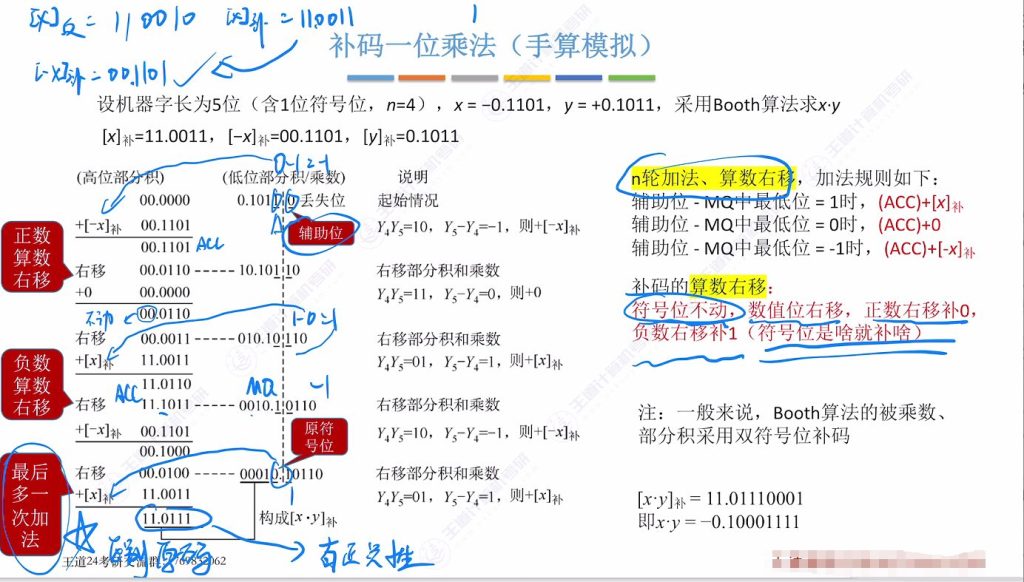
- 操作步骤:
- 初始化:辅助位设为0,MQ存储乘数补码
- 每轮判断:根据辅助位-MQ最低位差值决定加法操作
- 执行算术右移:符号位不变,数值位按符号补位
- 最终轮次:第n+1次只加法不移位
8.4 知识回顾
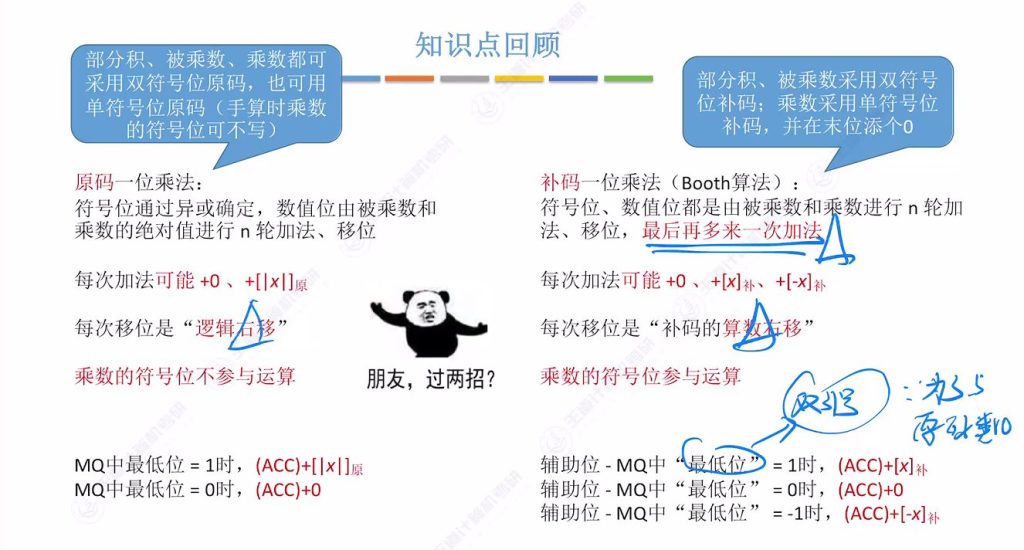
- 关键记忆点:
- 补码乘法的”多一次加法”特性
- 辅助位初始为0,通过右移动态更新
- 算术右移时负数需补1(如第三轮结果11.1011→11.1101)
- 易混淆点:
- MQ”最低位”实际指参与运算位(非真正的物理最低位)
- 最终加法需考虑乘数符号位(示例中y的符号位0参与运算)
- 运算验证:
- 示例结果[x⋅y]补=11.01110001对应真值-0.10001111
九、定点数原码除法运算

9.1 手算除法(十进制)

关键公式: x / y = a; 被除数/除数 = 商(余数b)
等价于: x = a * y +b
9.2 手算除法(二进制)

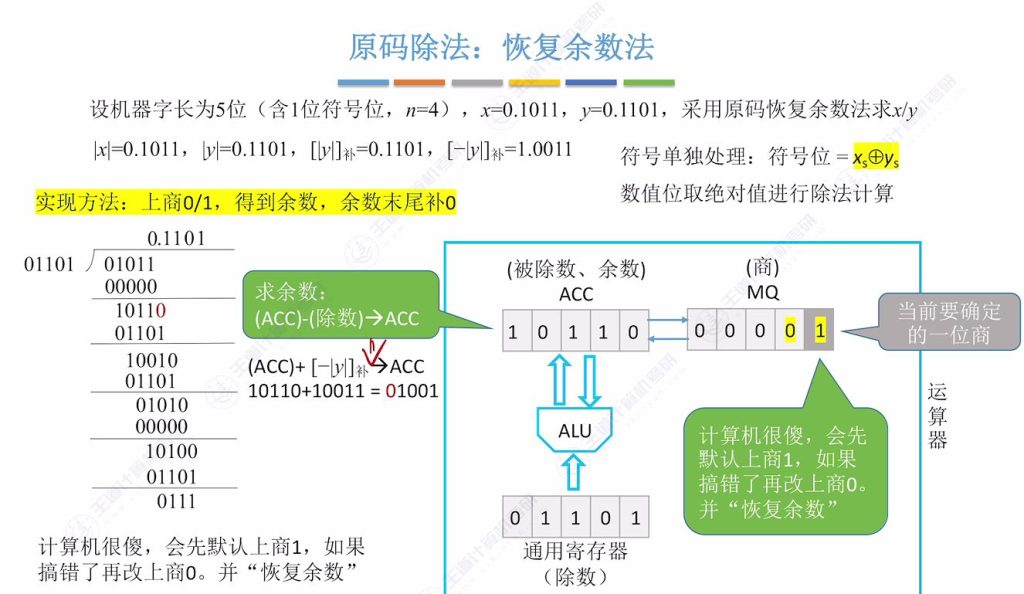
忽略小数点,每确定一位商,进行一次减法,得到4位余数,在余数末尾补0,再确定下一位商。
确定5位商即可停止(机器字长为5位)
9.3 运算器的基本组成
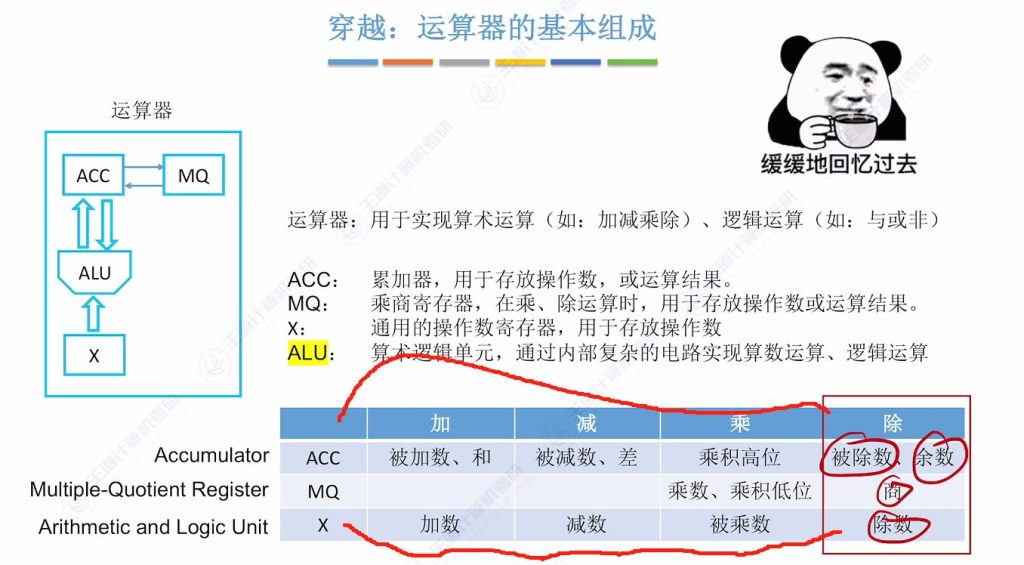
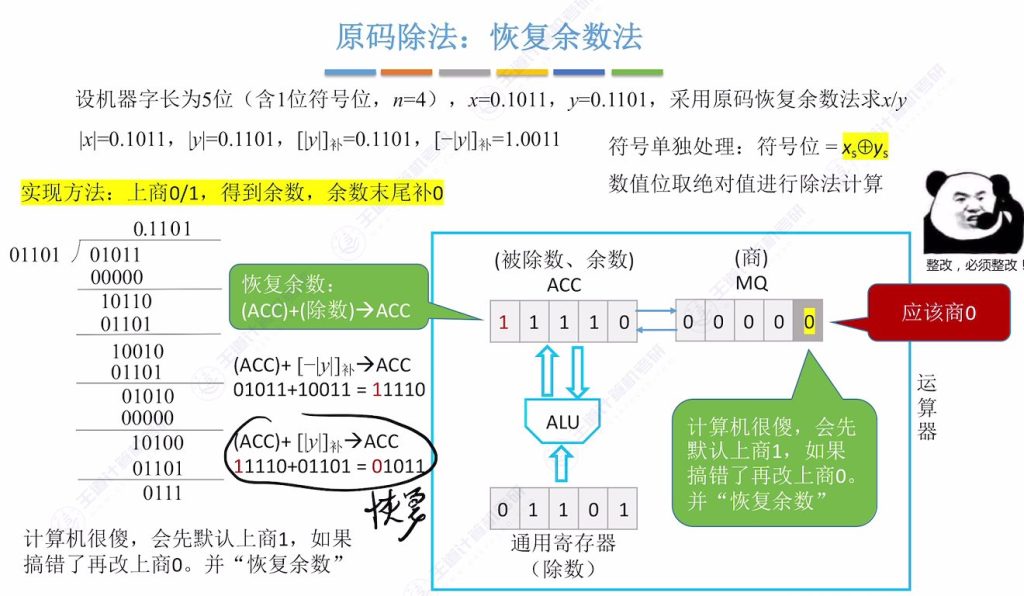
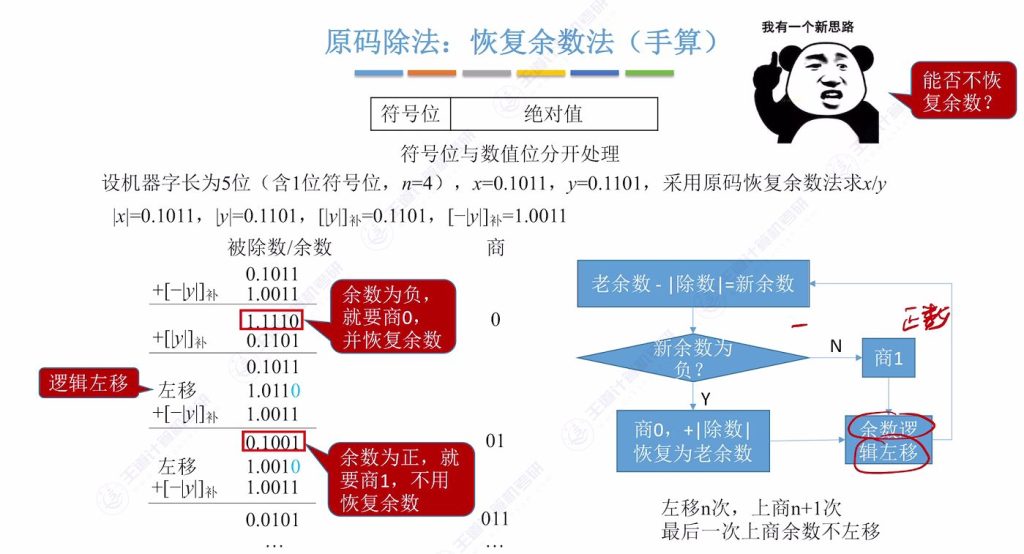
9.4 原码除法 – 恢复余数法
实现方法:上商 0/1,得到余数,余数末尾补0
符号处理:符号位单独通过异或运算确定
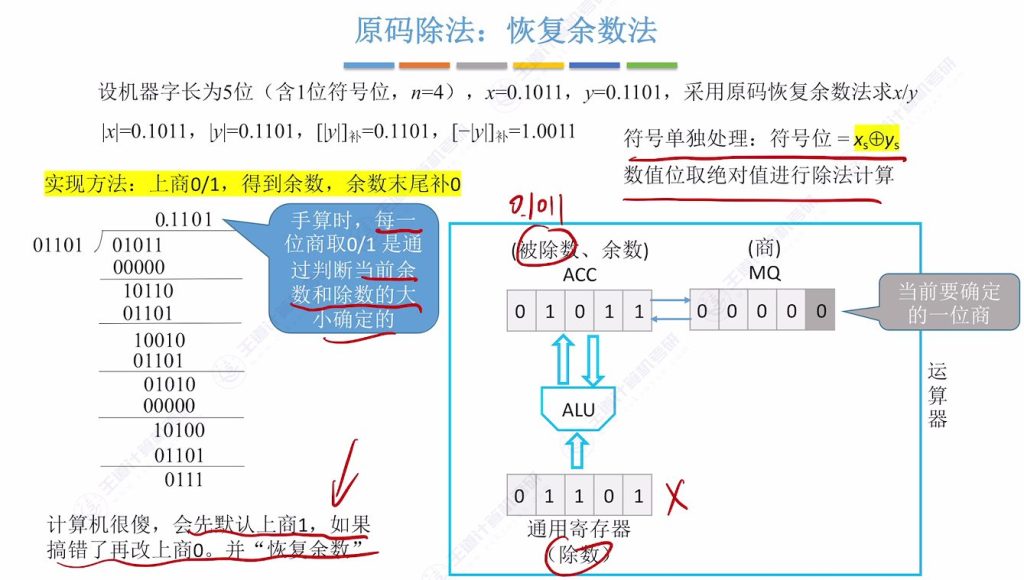
数值部分取绝对值进行除法计算
寄存器初始化:
- ACC寄存器存储被除数绝对值∣x∣=0.1011
- 通用寄存器存储除数绝对值∣y∣=0.1101及其补码形式
- MQ寄存器初始置零,末位标记当前待确定的商位
补码准备:
- [∣y∣]补=0.1101
- [−∣y∣]补=1.0011(用于减法操作的补码加法实现)
运算原理
默认策略:计算机默认每次商1,通过余数符号判断是否需要修正
修正机制:若余数为负(符号位为1),则:
- 将商由1改为0
- 执行ACC + [∣y∣]补 恢复正确余数
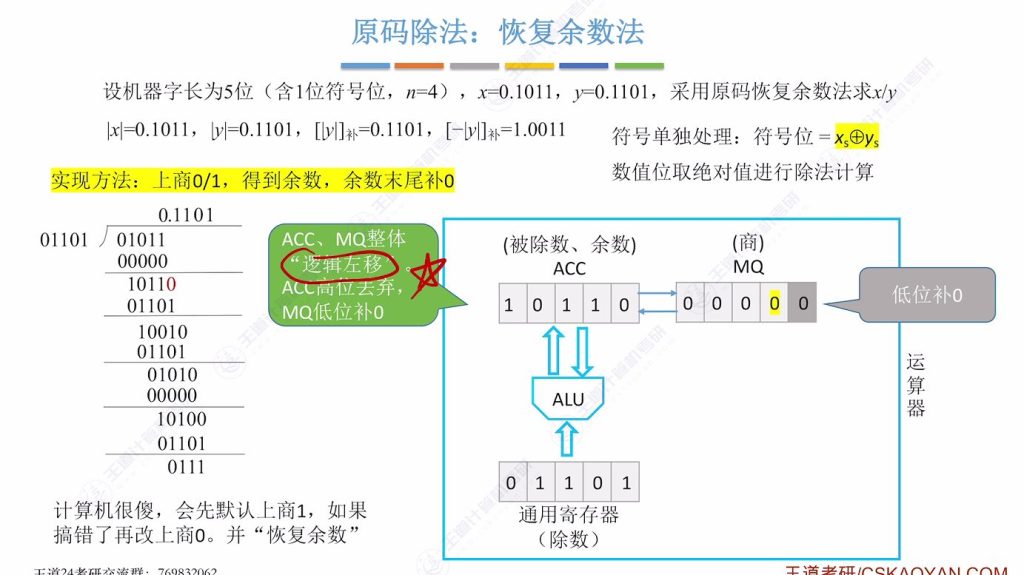
移位操作:每次确定商位后,ACC和MQ整体逻辑左移1位,低位补0
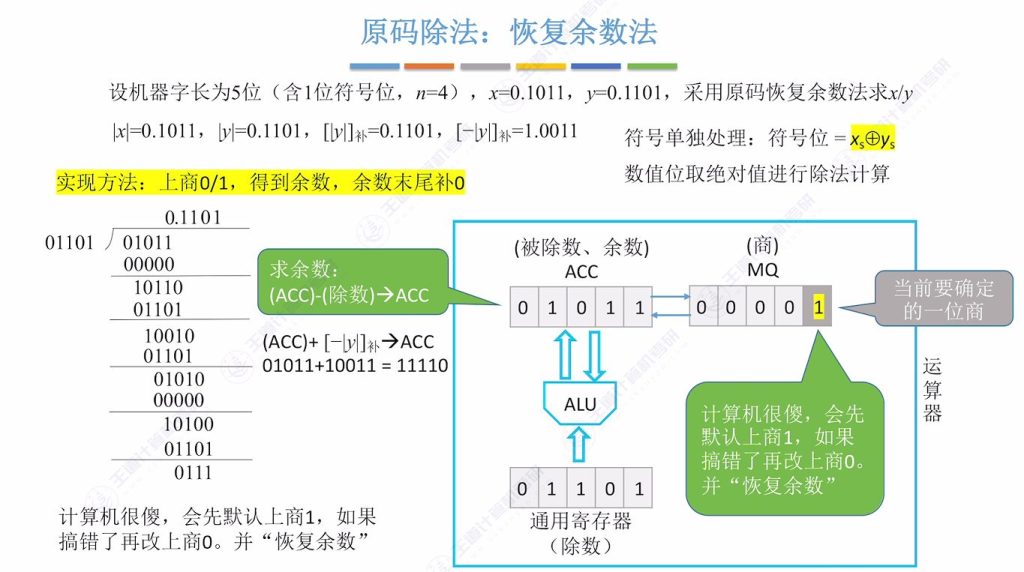
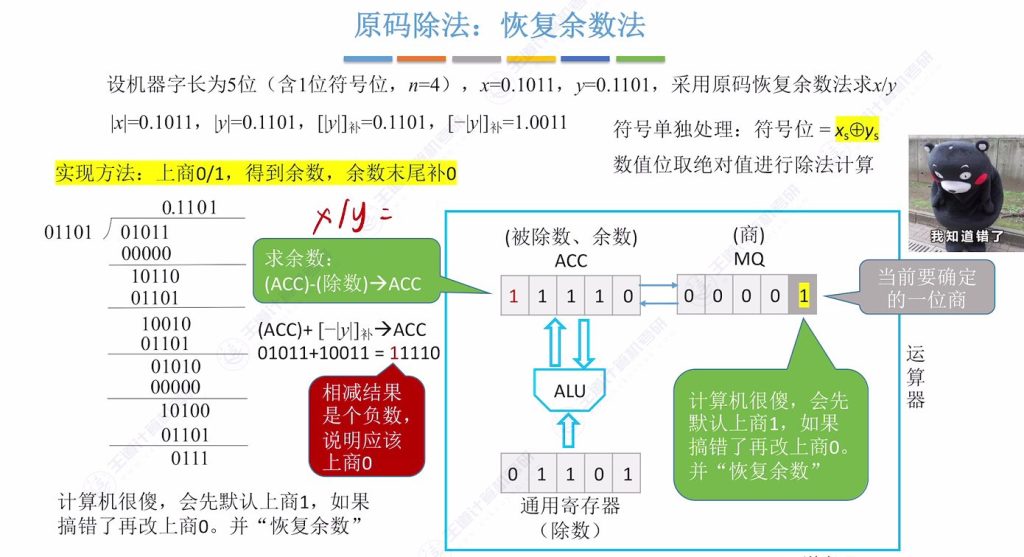
恢复余数
逻辑左移
循环计算机直接默认商1
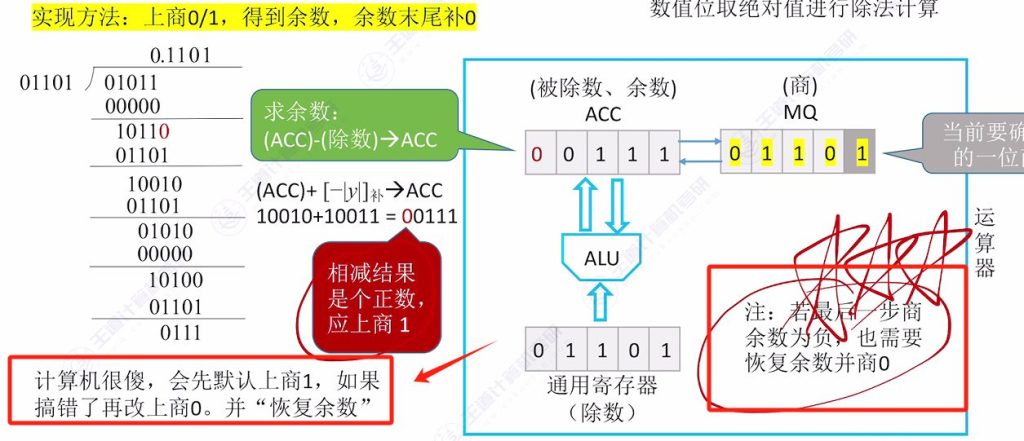
若最后一步商余数为负,也需要恢复余数并商 0
小数点的位置
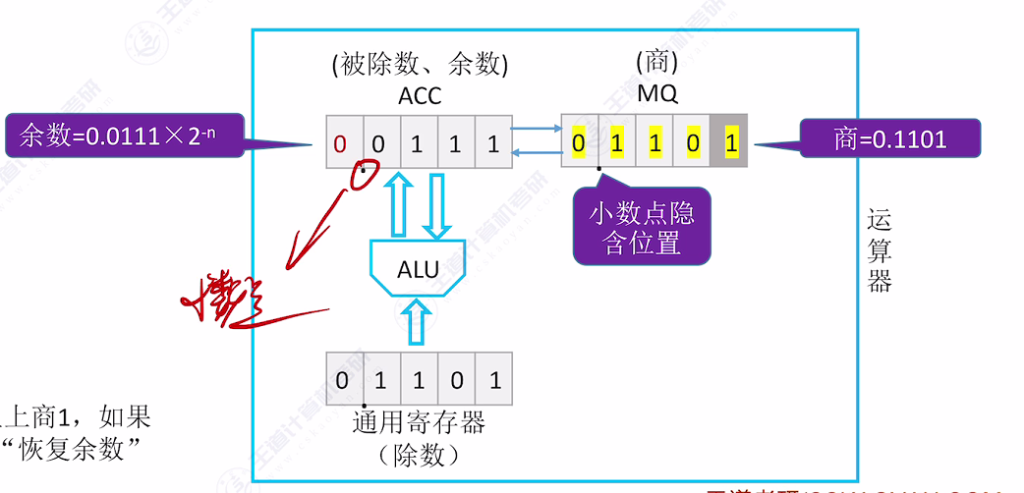
总结

- 注意事项:
- 终止条件:最后一步得到的余数若为负,仍需恢复余数并修正商
- 余数处理:最终余数需乘以2−n(n=4时为例)
- 硬件特点:计算机不具备直接比较功能,通过余数符号间接判断大小关系
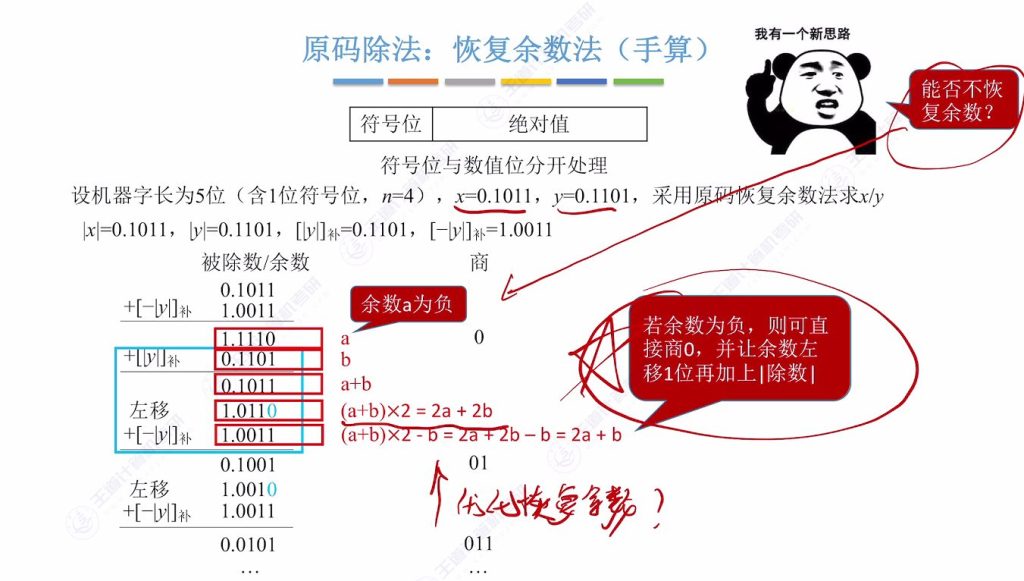
9.5 恢复余数法(手算)
9.6 恢复余数法(优化)
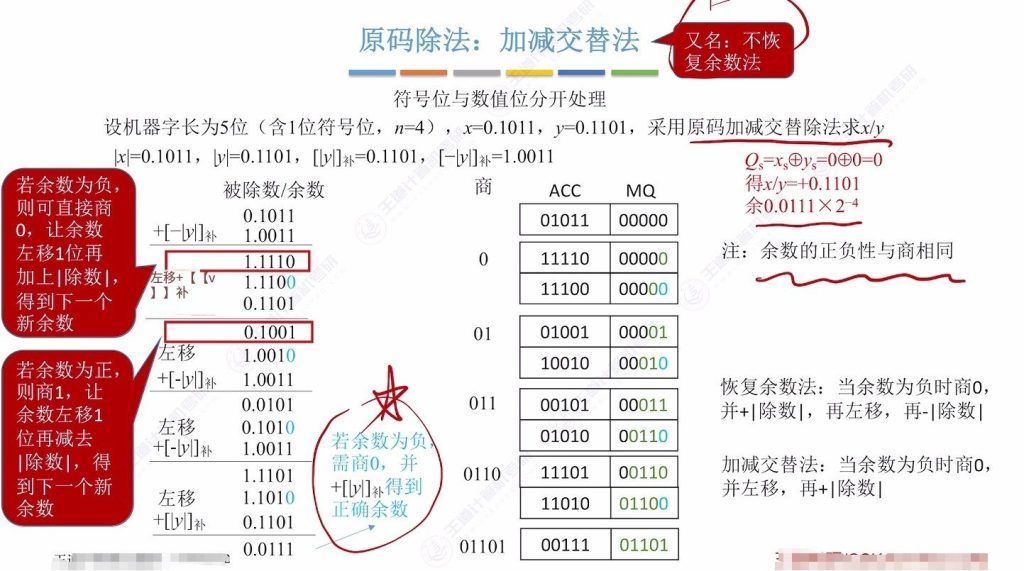
9.7 原码除法:加减交替法
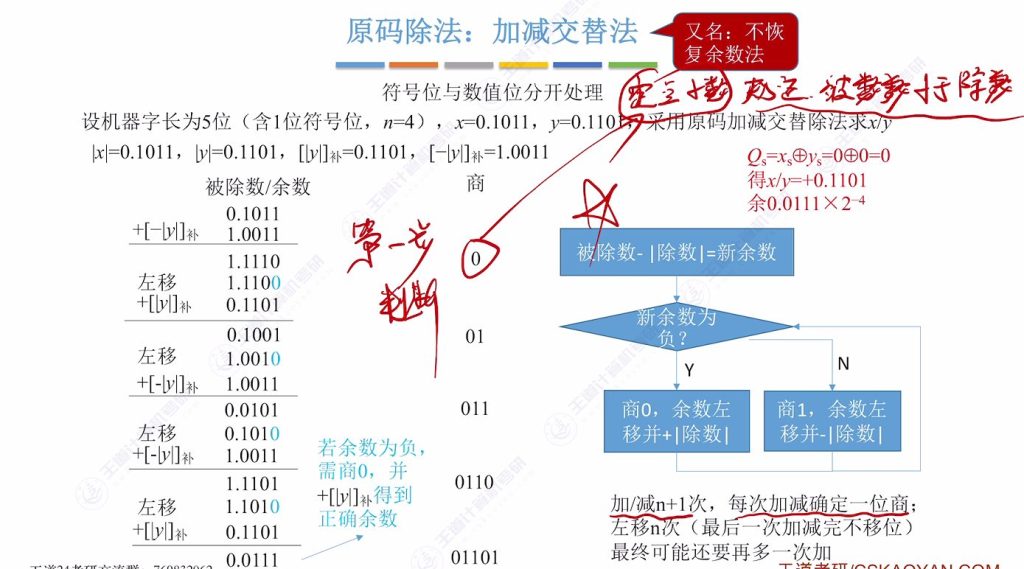
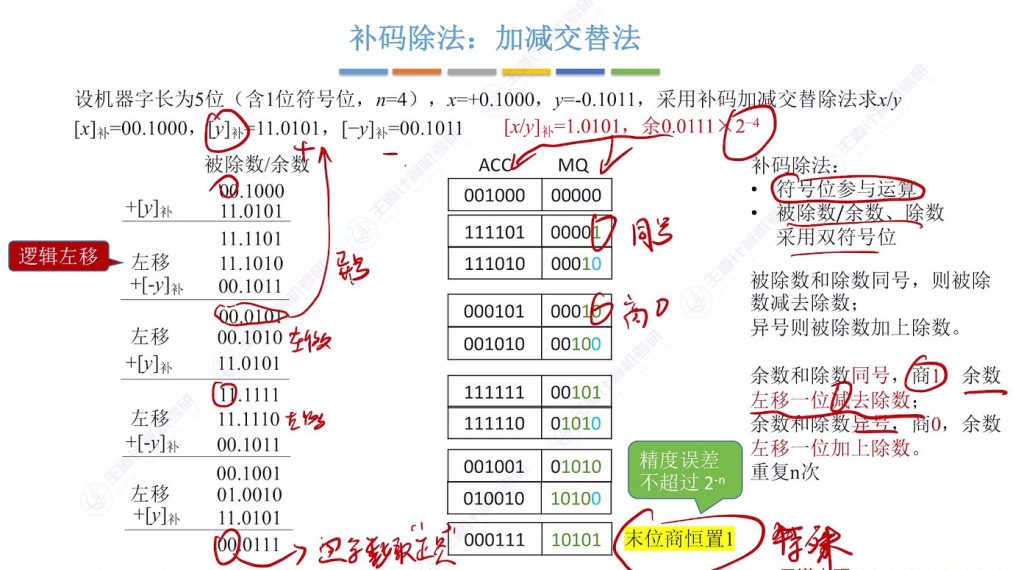
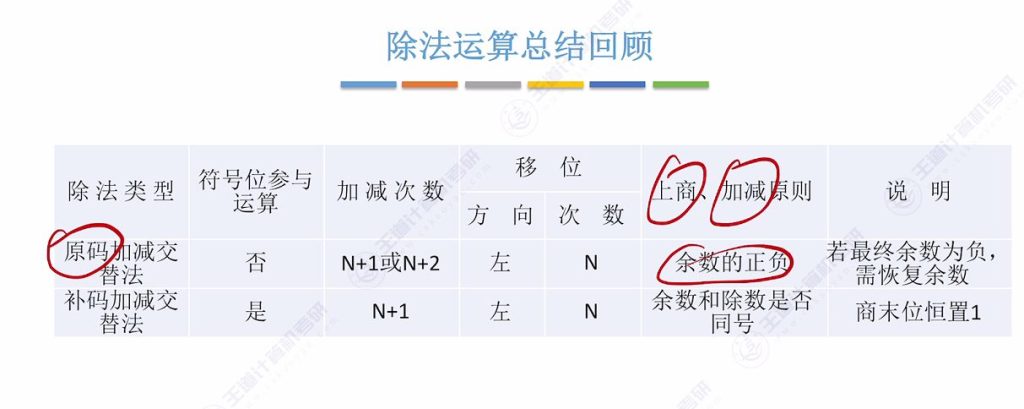
十、补码的除法运算
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客




