一、浮点数的表示
1.1 定点数的局限性

- 表示范围限制:定点数在字节数固定的情况下表示范围有限,如2字节short型只能表示-8540¥的个人负债,而4字节int型无法表示3000多亿的巨额财富。
- 扩展性问题:若将人民币换算为津巴布韦币,8字节long型也无法表示,说明单纯增加字节数不是解决方案。
1.2 从科学计数法理解浮点数
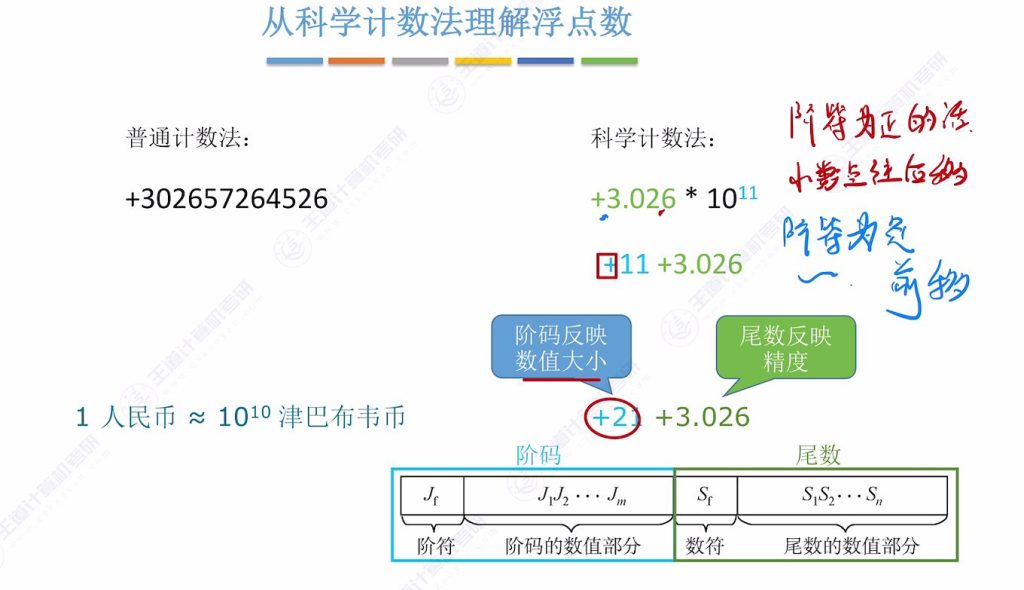
科学计数法
组成结构:
- 阶码:包含阶符(正负)和数值部分,决定小数点移动方向和位数。如:+3.026×1011中”+11″为阶码。
- 尾数:包含数符(整体正负)和数值部分,决定数字精度。尾数位数越多(如从3.026扩展到3.02657),精度越高。
1.3 浮点数的表示
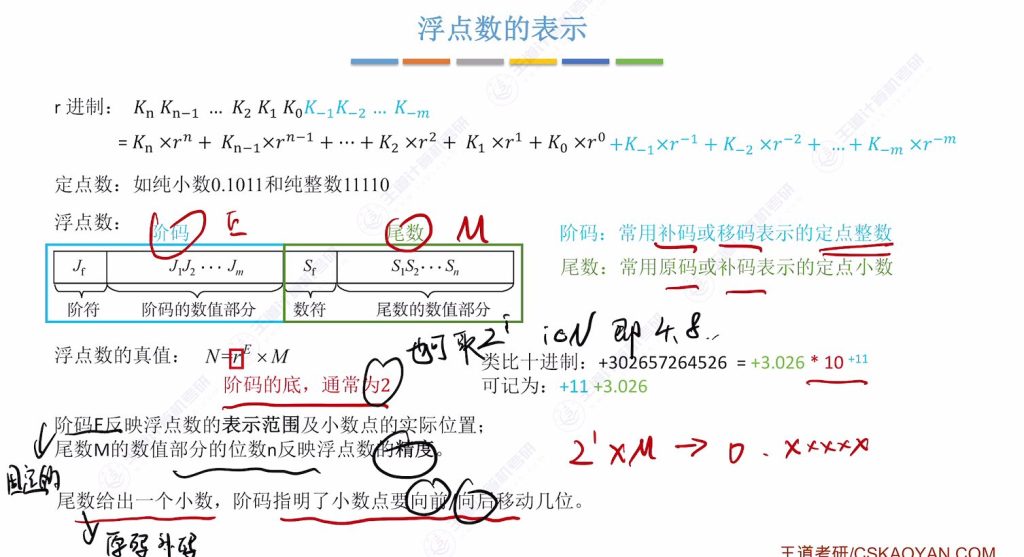
- 阶码:常用补码或移码表示的定点整数
- 尾数:常用原码或补码表示的定点小数
阶码
- 功能特性:
- 采用补码/移码表示的定点整数,底数通常为2(也可取4/8等2i值)。
- 反映数值范围:阶码位数限制决定最大/最小可表示值(类比十进制阶码两位数限制0-99)。
- 决定小数点位置:如阶码为1时,尾数需算术左移1位。
- 阶码底数取4时,阶码1对应小数点移动2位(类似十进制底数取100时阶码1移动2位)。
尾数
- 存储形式:原码/补码表示的定点小数,符号位决定整体正负。
- 精度决定:尾数数值部分位数n直接决定精度,n越大精度越高。如尾数”3.026″比”3.0″精度更高。
- 规格化要求:通常要求尾数绝对值在[0.5,1)范围内,通过调整阶码实现(类似科学计数法要求首位非零)
1.4 浮点数的表示案例
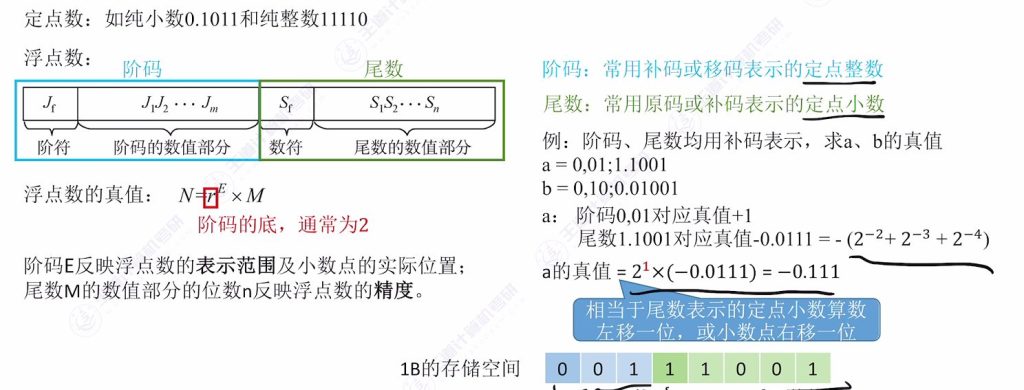
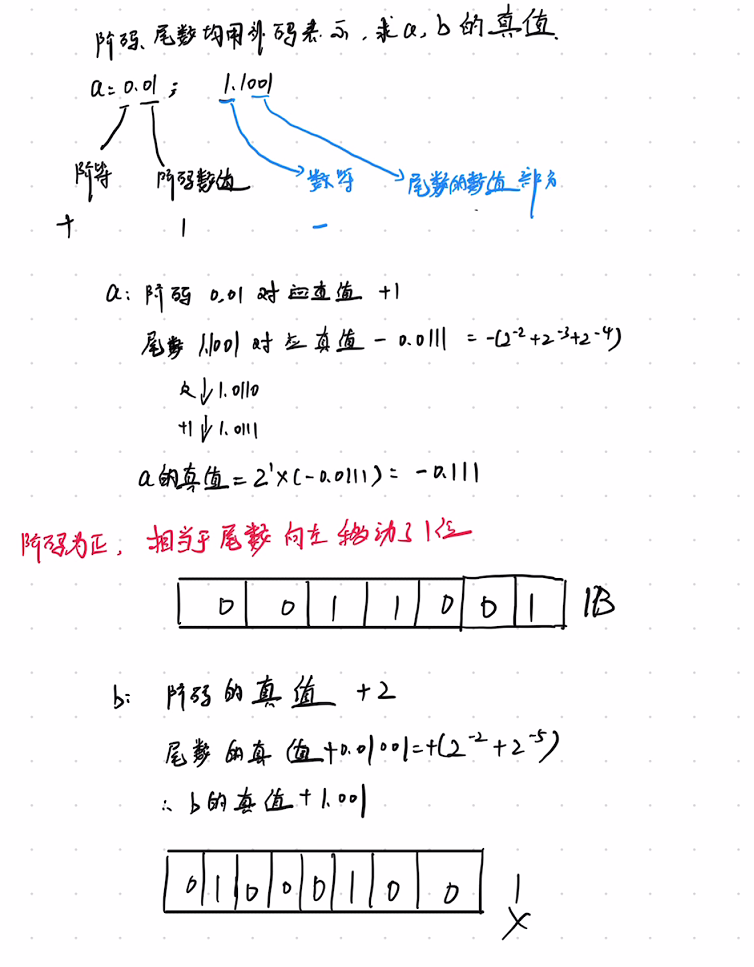
- 关键点
- 补码与原码的转换规则
- 阶码对小数点位置的影响
- 存储空间不足时的精度取舍问题
1.5 浮点数尾数的规格化
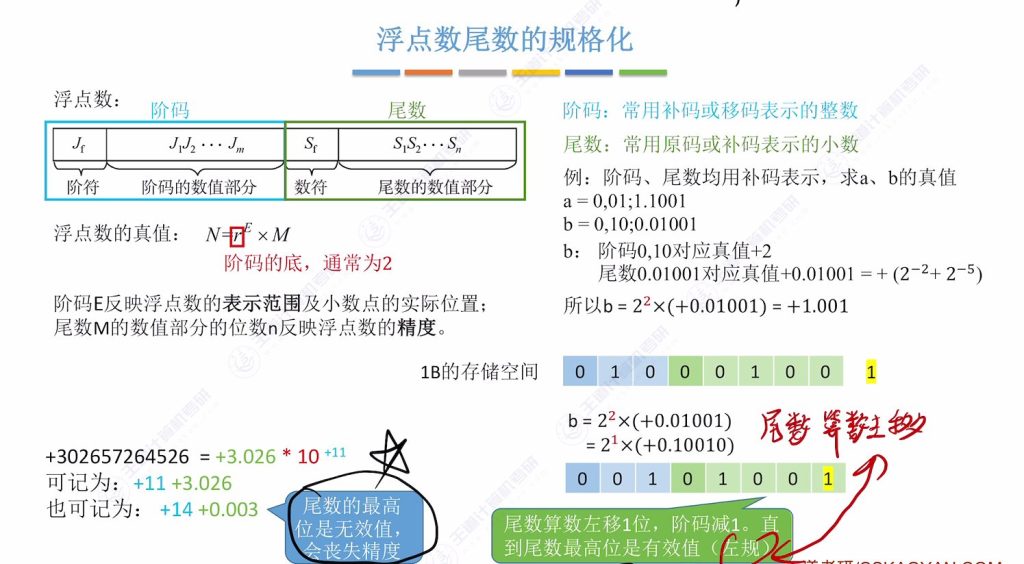
规格化浮点数
基本组成:浮点数由阶码和尾数组成,阶码常用补码或移码表示,尾数常用原码或补码表示
真值公式:N=rE×M,其中r为阶码的底(通常为2),E为阶码,M为尾数
规格化目的:通过保证尾数最高数值位为有效值,最大限度保留精度
十进制类比:类似科学计数法要求数值部分最高位非零(如3.026×10^11有效,0.003×10^14无效)
1.6 左规
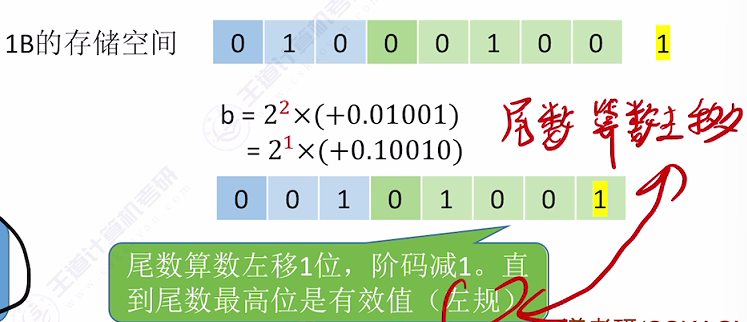
- 触发条件:尾数最高数值位无效(如二进制尾数为0.01001,首位0无效)
- 处理方法:
- 尾数算术左移1位(小数点右移)
- 阶码减1补偿
- 示例:b=0,10;0.01001 左规后变为0,01;0.10010,真值保持
- 特点:通过抛弃无效高位,在固定存储空间内增加有效位数
1.7 右规
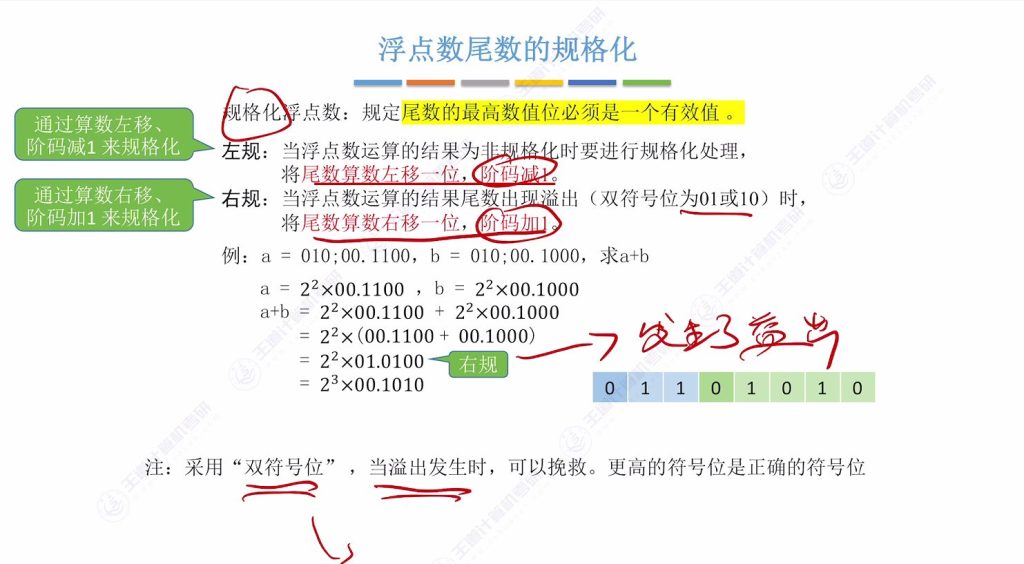
- 触发条件:运算导致尾数”假溢出”(双符号位为01或10)
- 处理方法:
- 尾数算术右移1位
- 阶码加1补偿
- 双符号位优势:高位符号位指示真实符号,可通过右规挽救溢出
1.8 浮点数尾数的规格化案例

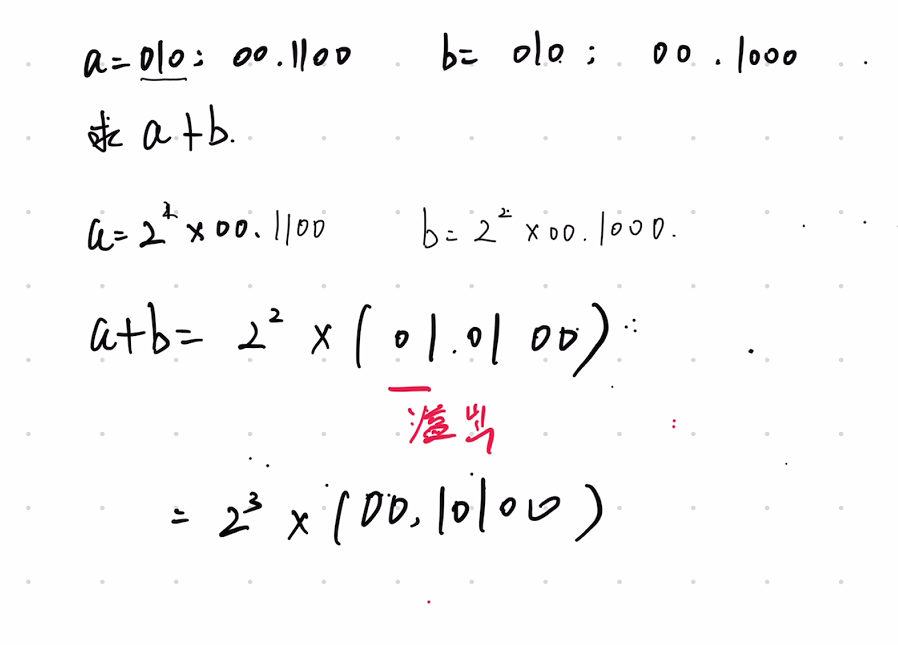
- 右规
- 对齐阶码后进行尾数相加
- 检测到双符号位01表示正溢出
- 执行右规操作:尾数右移1位补符号位,阶码+1
- 最终存储格式:|0|1|1|0|1|0|1|0|
1.9 规格化浮点数的特点

原码表示的尾数规格化

1、什么是规格化?
规格化就是将浮点数调整为标准格式,确保尾数的最高位是有效数字。
原码表示的尾数规格化是浮点数表示中的一个重要概念,目的是统一数的表示形式并提高精度。
2、原码尾数规格化的规则
对于原码表示:
- 正数:尾数的最高位必须是
1 - 负数:尾数的最高位必须是
1(因为原码中负数只是符号位为1,数值部分仍按正数处理)
3、规格化过程
步骤:
- 将尾数左移或右移
- 相应地调整阶码
- 直到尾数最高位为1
4、举例说明
例1:正数规格化
原始:0.001101 × 2³
规格化:1.101 × 2⁰- 尾数左移3位(去掉前导0)
- 阶码相应减3
例2:负数规格化(原码)
原始:-0.001011 × 2⁴
原码尾数:1.001011(符号位1,数值部分0.001011)
规格化后:1.1011 × 2¹5、规格化的意义
- 唯一性:每个非零数只有一种规格化表示
- 精度最大化:充分利用尾数的每一位
- 便于运算:统一的格式便于硬件实现
补码表示的尾数规格化

1、规格化条件
补码尾数规格化要求:
- 符号位与最高数值位必须不同
- 这样可以避免冗余表示,提高精度利用率
2、规格化格式
正数格式: 0.1 × x...x
- 符号位:0(正数)
- 最高位:1(与符号位不同)
- 后续位:任意组合
负数格式: 1.0 × x...x
- 符号位:1(负数)
- 最高位:0(与符号位不同)
- 后续位:任意组合,但整体符合补码规则
3、表示范围分析
正数范围: 1/2 ≤ M ≤ (1 - 2^(-n))
- 最小值:0.100…0 = 1/2
- 最大值:0.111…1 = 1 – 2^(-n)
负数范围: -1 ≤ M ≤ -(1/2 + 2^(-n))
- 最大值(最接近0):1.011…1 = -(1/2 + 2^(-n))
- 最小值:1.000…0 = -1
4、移位规则
算术左移: 低位补0
- 用于规格化时将有效位左移
- 保持符号位不变
算术右移: 高位补1
- 用于非规格化调整
- 保持数值的符号特性
5、规格化过程示例
正数规格化:
原始:0.001101 × 2³
规格化:0.1101 × 2⁰负数规格化:
原始:1.110011 × 2²(已规格化,符号位1,最高位1,需调整)
应为:1.011001 × 2¹(符号位1,最高位0)6、关键优势
- 对称性:正负数范围相对对称
- 精度最大化:避免了前导位的浪费
- 运算便利:补码运算规则统一
- 硬件友好:移位操作简单高效
7、与原码的对比

1.10 规格化浮点数计算案例

- 题目解析
- 初始值:0.110;1.1110100(阶码4位,尾数8位)
- 尾数为负数补码,需满足符号位与最高数值位相反
- 执行算术左移3次:尾数变为1.0101000
- 阶码补偿:+6→+3(011)
- 最终规格化结果:011;1.0101000
1.11 知识点回顾
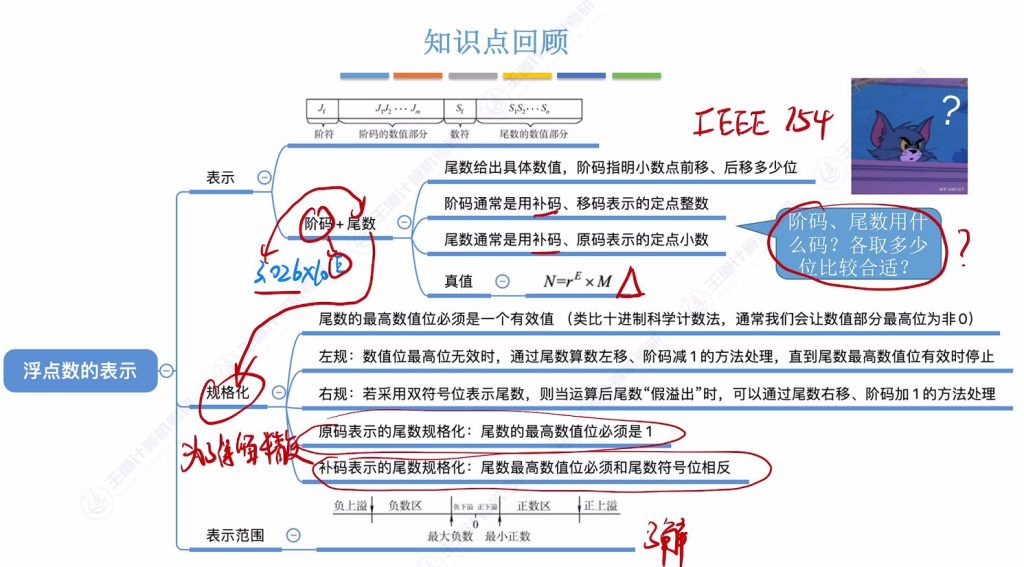
- 表示原理:通过rE×M现动态小数点位,阶码决定范围,尾数决定精度
- 规格化本质:保证尾数最高数值位有效(原码为1,补码与符号位相反)
- 异常类型:
- 上溢:超出最大表示范围(正/负上溢)
- 下溢:小于最小正数/最大负数(正/负下溢)
- 移位规则:
- 左规:尾数左移,阶码减
- 右规:尾数右移,阶码加
二、浮点数标准 IEEE 754
I triple e 754
2.1 移码
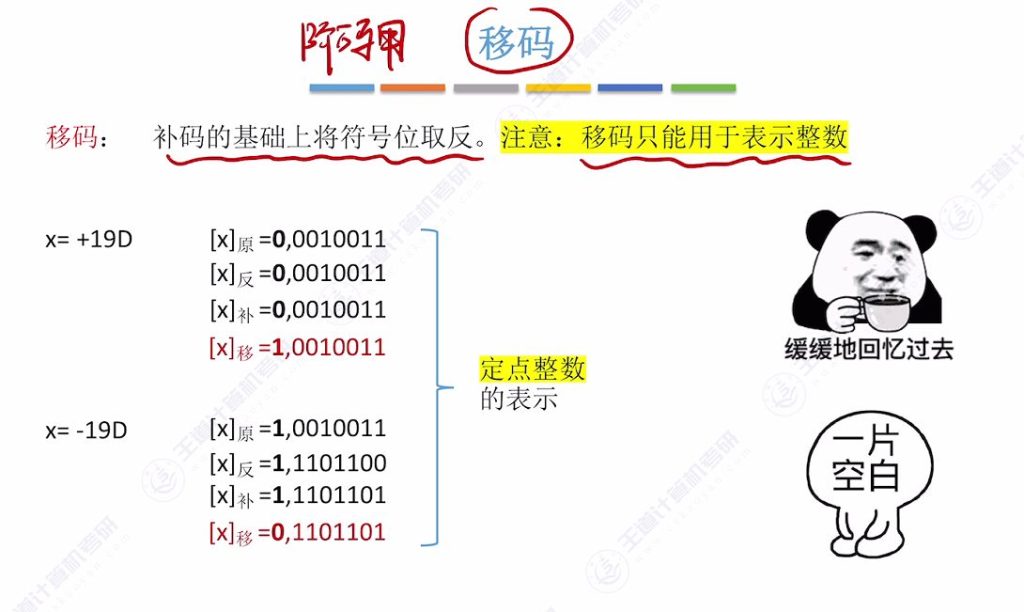
移码的基本概念与计算方法
移码是在补码的基础上将符号位取反得到的编码方式,只能用于表示整数。
2.2 标准偏置值
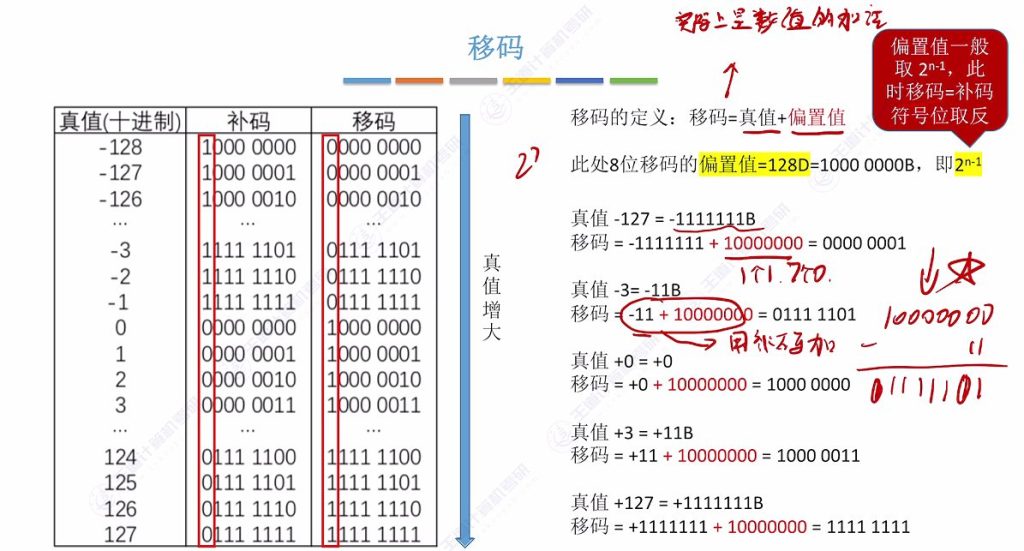
移码的定义实际上是数值的加法实现的
移动 = 真值 + 偏置值
移码(偏移二进制码)的核心思想是将负数区间整体”移动”到正数区间来表示。
基本原理:
- 真码:直接的二进制表示,有正负之分
- 偏置值:一个固定的正数,通常是 2^(n-1),其中n是位数
- 移码 = 真码 + 偏置值
举个简单例子(4位):
- 偏置值 = 2³ = 8
- 真码 -5 → 移码:-5 + 8 = 3 → 二进制 0011
- 真码 +3 → 移码:+3 + 8 = 11 → 二进制 1011
为什么这样做?
- 统一处理:把所有数(包括负数)都变成正数来存储
- 简化比较:移码可以直接按无符号数比较大小
- 应用场景:主要用在浮点数的指数部分
简单说就是给所有数都加上一个固定值,让原本的负数变成正数来表示,这样处理起来更方便。
2.3 IEEE 754 特殊偏置值
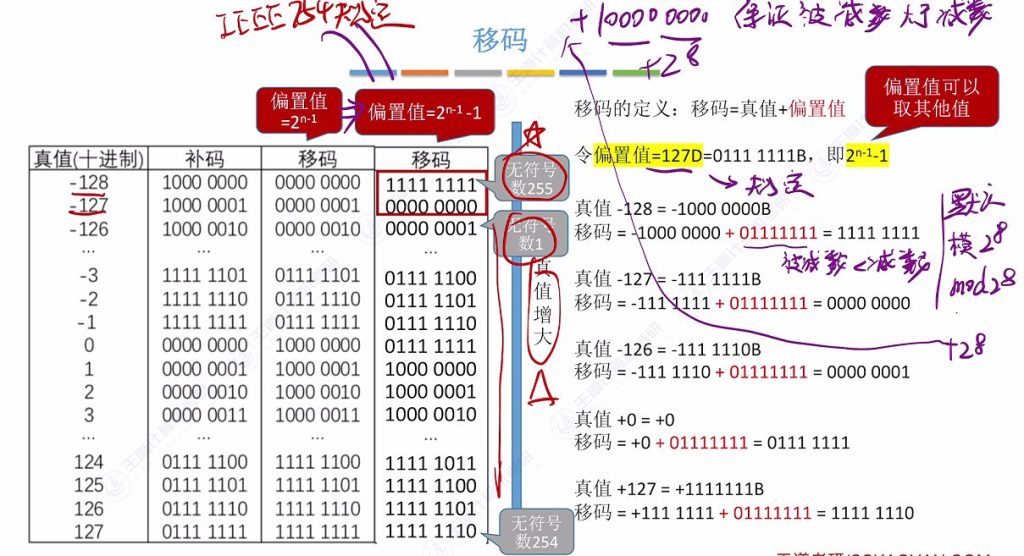
IEEE 754标准中的特殊偏置值是为了表示浮点数而设计的偏移量
偏置值的作用:
- 将有符号的指数转换为无符号存储格式
- 使得指数的比较可以直接通过二进制比较进行
具体数值:
- 单精度(32位):偏置值为127
- 双精度(64位):偏置值为1023
计算方法: 偏置值 = 2^(k-1) – 1,其中k是指数位数
- 单精度:2^(8-1) – 1 = 127
- 双精度:2^(11-1) – 1 = 1023
使用方式:
- 存储时:实际指数 + 偏置值 = 存储的指数
- 读取时:存储的指数 – 偏置值 = 实际指数
举例: 如果实际指数是-3,在单精度中存储为:-3 + 127 = 124
这种设计使得浮点数的指数部分总是正数,简化了硬件实现和比较操作。
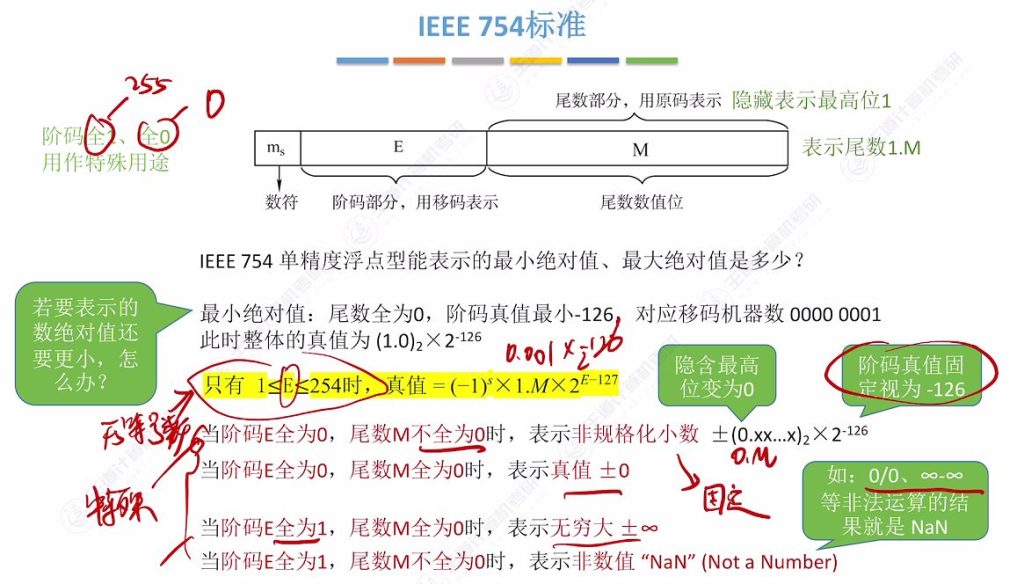
阶码全1、全0用作特殊用途
全1:1111 1111B – 无符号255
全0:0000 0000B – 无符号1
2.4 IEEE 754标准
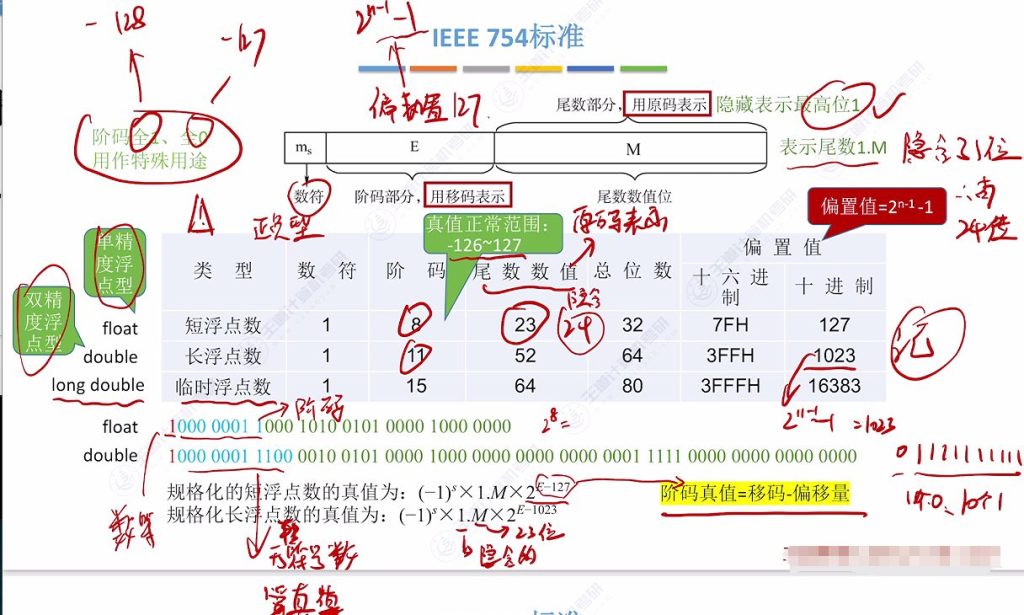
IEEE 754标准是定义浮点数算术运算的国际标准,于1985年首次发布,并在2008年进行了重大修订。这个标准规定了浮点数的表示格式、算术运算规则以及异常处理方式,是现代计算机系统中浮点运算的基础。
通用结构
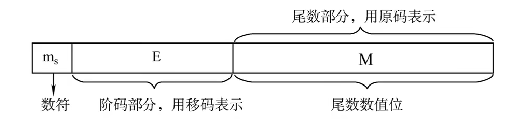
数符(1位):表示正负
阶码(移码表示):偏置值专属 IEEE 754的标准
尾数(原码表示):隐含最高位1
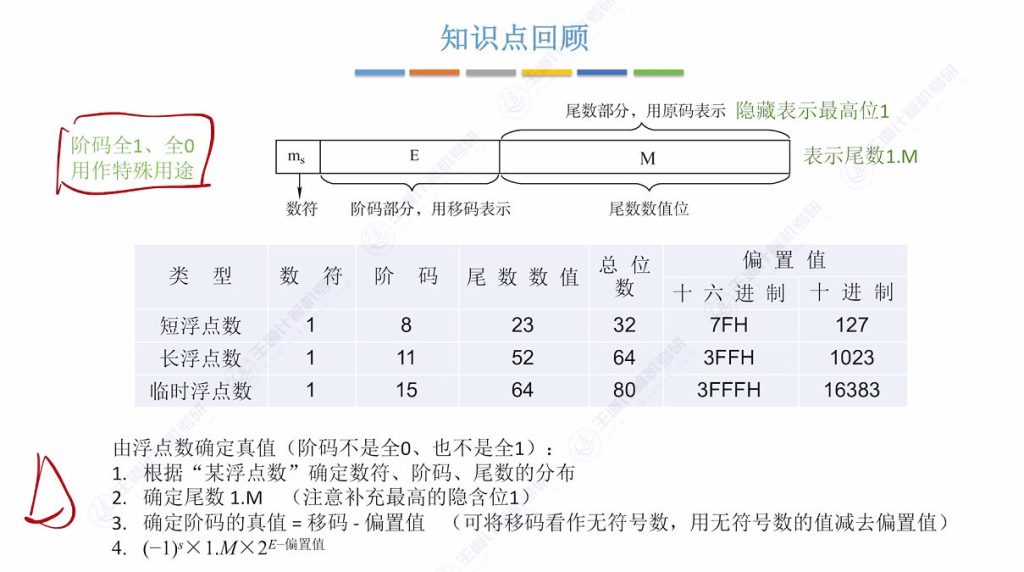
具体类型
短浮点数(float):
- 总位数:32位(1+8+23)
- 偏置值:127D(7FH)
- 尾数处理:实际24位(1.xxx)
长浮点数(double):
- 总位数:64位(1+11+52)
- 偏置值:1023D(3FFH)
临时浮点数(long double):
- 总位数:80位(1+15+64)
- 偏置值:16383D(3FFFH)
2.5 例题:十进制转浮点数
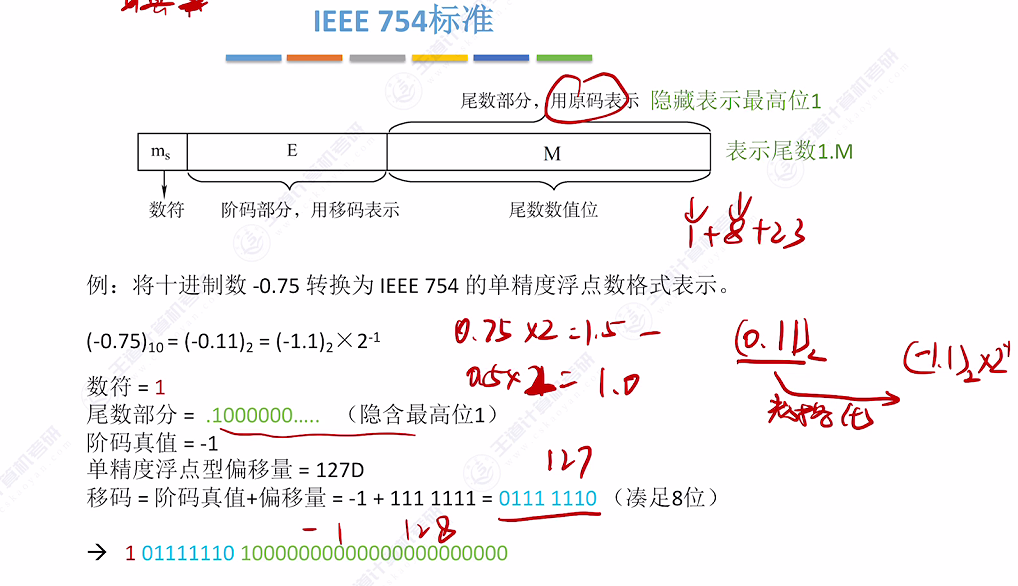
- 转换步骤
- 规格化处理:将二进制数转换为1.xxx形式,如-0.75(-0.11₂)规格化为-1.1×2⁻¹
- 数符确定:负数取1,正数取0
- 尾数处理:隐含最高位1,实际存储小数点后部分(1.1→存储100…0)
- 阶码计算:真值(-1)+偏移量(127)=126→01111110₂
- 单精度格式
- 结构组成:1位数符 + 8位阶码(移码) + 23位尾数(原码)
- 偏移量:单精度固定为127(双精度为1023)
- 完整示例:-0.75最终表示为1 01111110 10000000000000000000000
2.6 例题:浮点数转十进制
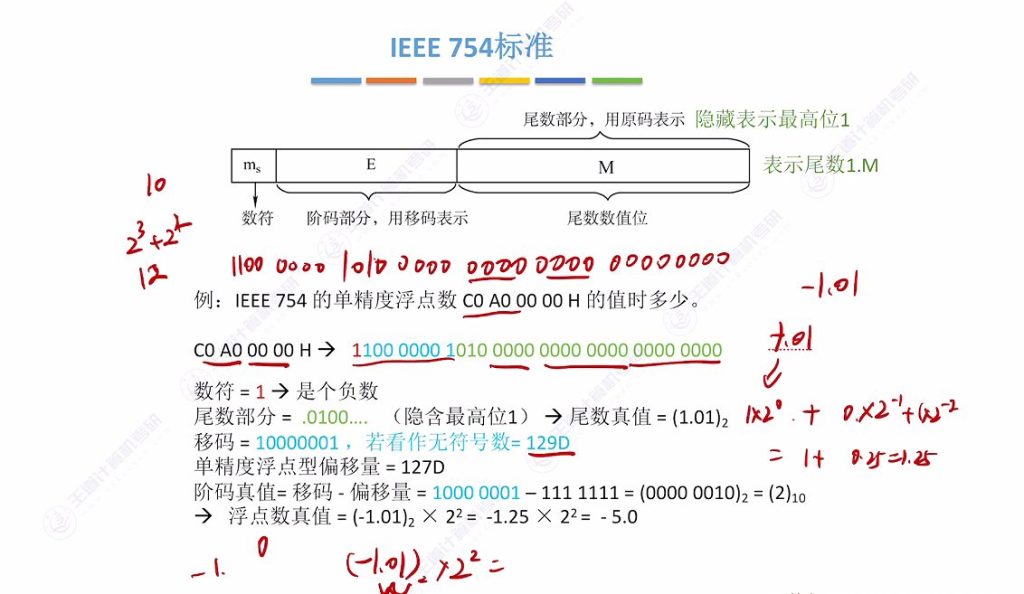
- 解析步骤
- 十六进制转换:如COAO0000H→110000001010…0
- 数符判断:首位1表示负数
- 尾数还原:补上隐含1→1.01₂(即1.25₁₀)
- 阶码转换:10000001₂→129₁₀,真值=129-127=2
- 结果计算:-1.25×2²=-5.0
2.7 例题:单精度浮点数绝对值
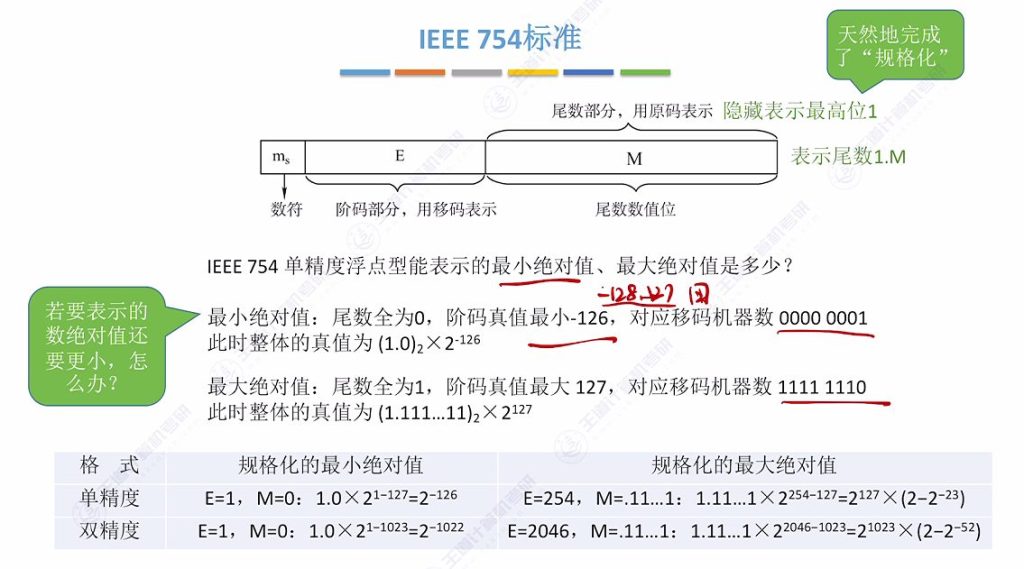
可以通过编程验证这些值:
#include <stdio.h>
#include <float.h>
int main() {
printf("单精度浮点数范围:\n");
printf("最大值:%.7e\n", FLT_MAX);
printf("最小规格化数:%.7e\n", FLT_MIN);
printf("最小非规格化数:%.7e\n", FLT_TRUE_MIN);
printf("精度:%d位有效数字\n", FLT_DIG);
return 0;
}2.8 IEEE 754的特殊表示
2.9 知识回顾
三、浮点数加减法运算
3.1 浮点数加减运算步骤
一共 5 步运算:对阶、尾数加减、规格化、舍入、判断溢出
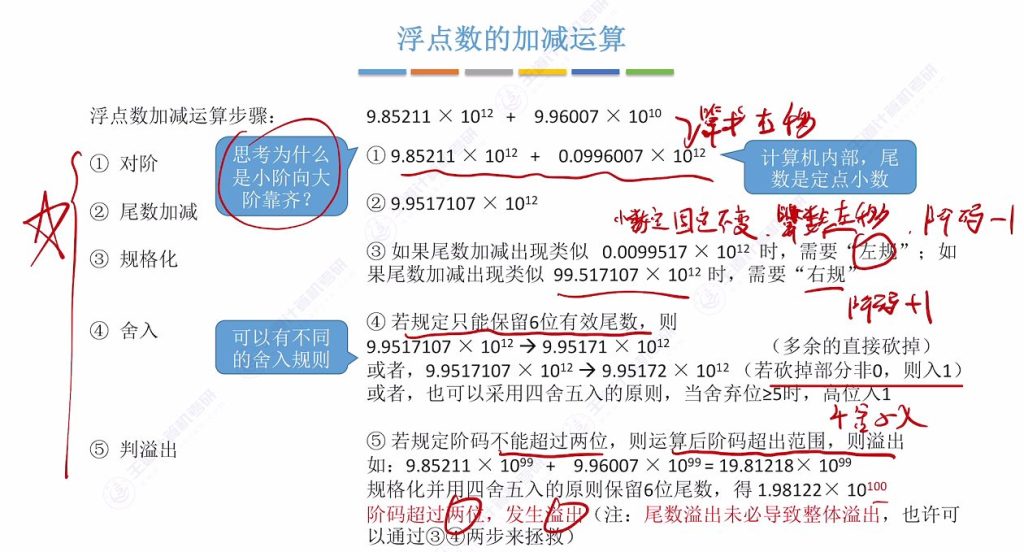
step 01 对阶
- 基本原则: 小阶向大阶对齐,通过算术右移实现
- 原因分析:
- 计算机处理定点小数时,小数点位置固定
- 大阶向小阶对齐会导致小数点前出现多个有效位,硬件实现困难
- 小阶向大阶对齐只需算术右移,硬件实现简单
- 阶差计算: 通过两数阶码相减判断大小关系,差值为负说明被减数阶码更小
step 02 尾数相减
- 操作要点:
- 阶码对齐后才能进行尾数运算
- 减法转换为加法实现(取负数的补码)
- 双符号位补码运算时,最高位进位丢弃
- 溢出特征: 双符号位不同表示尾数溢出,但可通过规格化修正
step 03 规格化
- 左规条件: 尾数出现0.00…..形式时
- 操作:尾数算术左移,阶码减1
- 右规条件: 尾数出现xxxxxx.xx形式(小数点前多位非零)时
- 操作:尾数算术右移,阶码加1
- 规格化标准: 确保尾数第一个数值位为有效位(非零)
step 04 舍入
- 必要性: 浮点数尾数位数有限,运算后可能超出存储长度
- 常见策略:
- 直接截断(砍掉低位)
- 非零进一(舍弃部分非零时向高位进1)
- 四舍五入(舍弃部分≥0.5时进1)
- 二进制特点: 舍入规则与十进制类似,但基于二进制位判断
step 05 判溢出
- 判断标准: 仅阶码溢出才是真正溢出
- 尾数溢出可通过规格化修正
- 检测方法:
- 双符号位补码:符号位不同表示溢出
- 阶码超出表示范围时发生溢出
- 重要区别: 尾数溢出可恢复,阶码溢出不可恢复
3.2 例题:浮点数的加减运算(考试标准)
1、十进制转为双符号位二进制补码

2、对阶计算,求阶差,为了使得两个数的阶数相同,小阶向大阶看齐
- -1 尾数右移,阶码+1
- 1 尾数左移,阶码-1

3、尾数相加
X-Y转化为X+Y,对 Y全部取反+1

4、规格化、舍入、判溢出

- 运算过程:
- 对阶:阶差为-1,X右移1位,阶码+1
- 尾数减:取Y的负数补码相加
- 规格化:右归处理尾数溢出
- 舍入:本例无舍入需求
- 判溢出:双符号位相同,无溢出
3.3 舍入

“0”舍”1″入法
- 原理:类似于十进制中的”四舍五入”,在尾数右移时,被移去的最高数值位为0则舍去;为1则在尾数末位加1。
- 潜在问题:加1操作可能导致尾数再次溢出,此时需要再做一次右规操作。
- 示例:尾数加减结果为11100,10.110001011时,若右移舍弃的位为1,则需在末位加1变为11101,11.0110001011。
恒置”1″法
- 操作规则:尾数右移时,不论丢弃的最高数值位是0还是1,都将右移后的尾数末位恒置为1。
- 特点:这种方法会使尾数可能变大或变小,但避免了”0舍1入”法中可能的二次溢出问题。
浮点数加减运算中的舍入问题
- 运算步骤:1.对阶 → 2.尾数加减 → 3.规格化 → 4.舍入 → 5.判溢出
- 特殊处理:某些计算机将24bit尾数扩展为32bit计算,完成运算后再舍入截断回24bit,此时同样面临舍入问题。
- 溢出处理:阶码超出上限为上溢(需抛出异常),低于下限为下溢(当作机器0处理)。
3.4 强制类型转换
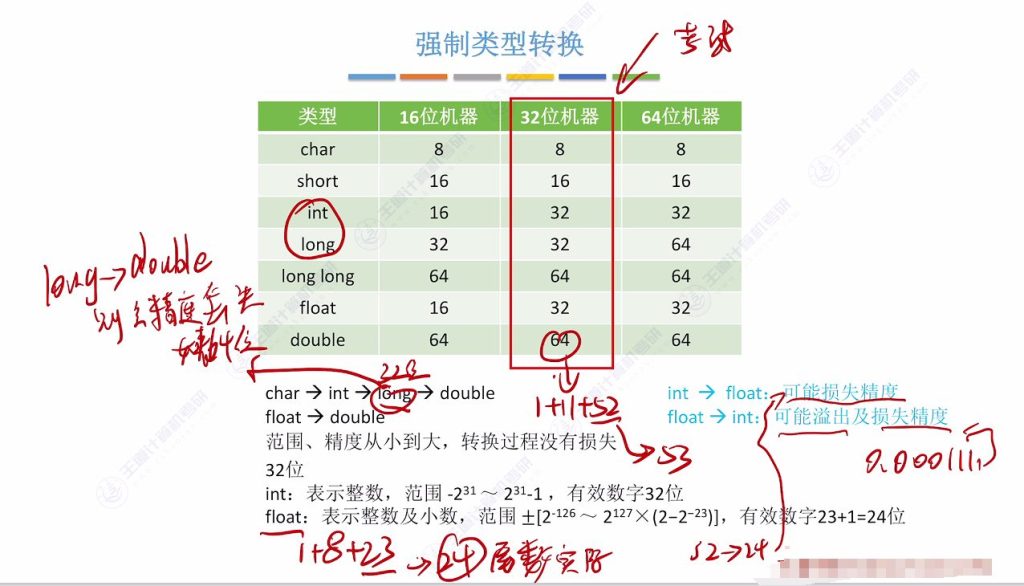
不同机器的数据类型长度
- 关键差异:int型在16位机器占16位,32/64位机器占32位;long型在32位机器占32位,64位机器占64位。
32位机器的数据类型特点
- 考试重点:多数教材基于32位环境编写,考试通常考察32位情况下的转换。
- 典型配置:int=32bit,long=32bit,double=64bit(1符号位+11阶码+52尾数,隐含1位实际53位有效数值)。
无损的强制类型转换
- char→int:8位→32位,保留全部信息
- short→int:16位→32位,保留全部信息
- long→int:32位→32位,等宽转换
- float→double:尾数从24位(1+23)扩展到53位(1+52),阶码从8位扩展到11位
long型向double型转换的精度问题
- 32位情况:32位long可被53位double尾数完整表示,无精度损失
- 64位情况:64位long超出53位表示能力,会有精度损失(考试通常不考此情况)
float型向double型转换
- 精度保证:float尾数24位 < double尾数53位
- 范围保证:float阶码8位 < double阶码11位
int型向float型转换的精度损失
- 原因分析:int型31位有效数值 > float型24位尾数
- 范围特性:float表示范围更大,不会溢出但会损失精度
float型向int型转换的溢出与精度损失
- 溢出风险:float表示范围远大于int,可能发生正/负上溢
- 精度损失:小数部分会被直接截断(如0.000111→0)
- 典型场景:float表示的小数转换为int时必然丢失小数部分
3.5 知识回顾
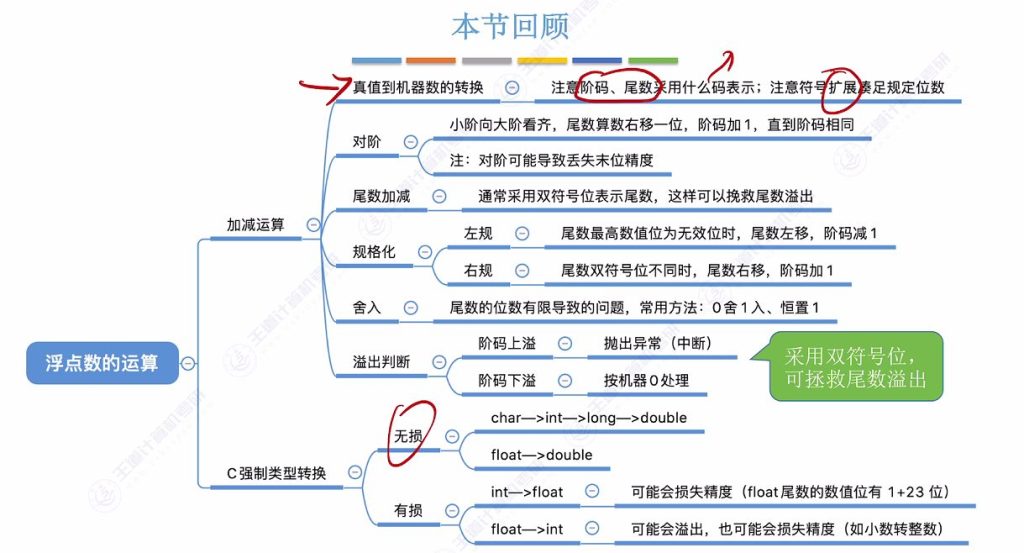
四、数列的存储和排列
4.1 大小端模式
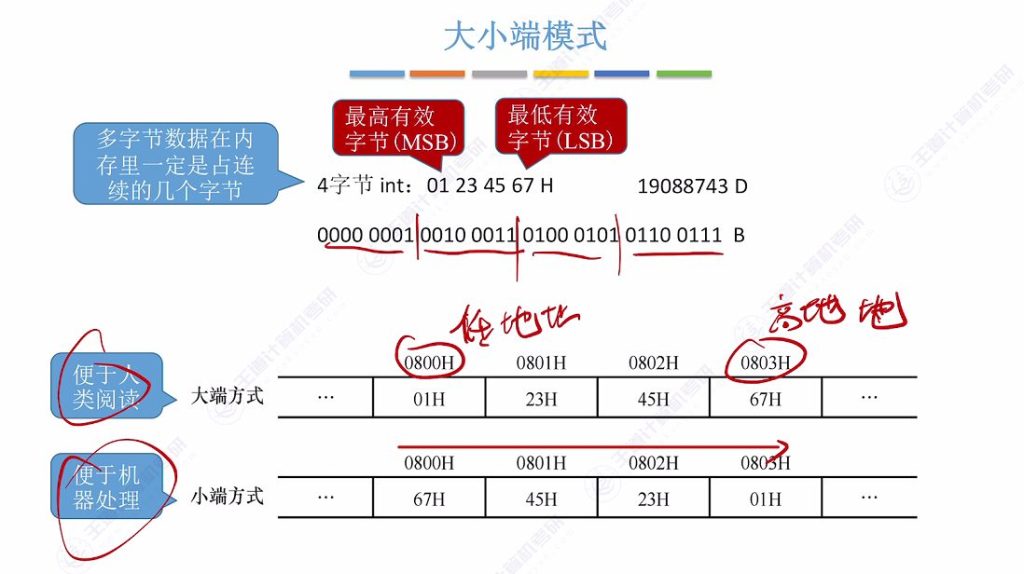
1、多字节数据存储:在内存中存储多字节数据(如C语言的int型变量)时,会占据连续的几个字节空间。
例如4字节int型变量用16进制表示为01 23 45 67H,对应十进制19088743
2、有效字节区分:
- MSB(最高有效字节):数据最左边的字节(如示例中的01)
- LSB(最低有效字节):数据最右边的字节(如示例中的67H)
3、存储模式分类:
- 大端模式:符合人类阅读习惯,将最高有效字节存储在最低内存地址
- 小端模式:机器处理更高效,将最低有效字节存储在最低内存地址
4、机器处理优势:
- CPU按地址递增顺序读取数据,小端模式会先读取最低有效字节
- 进行多字节运算(如加法)时,CPU需要从低位开始处理,小端模式可直接顺序处理
4.2 边界对齐
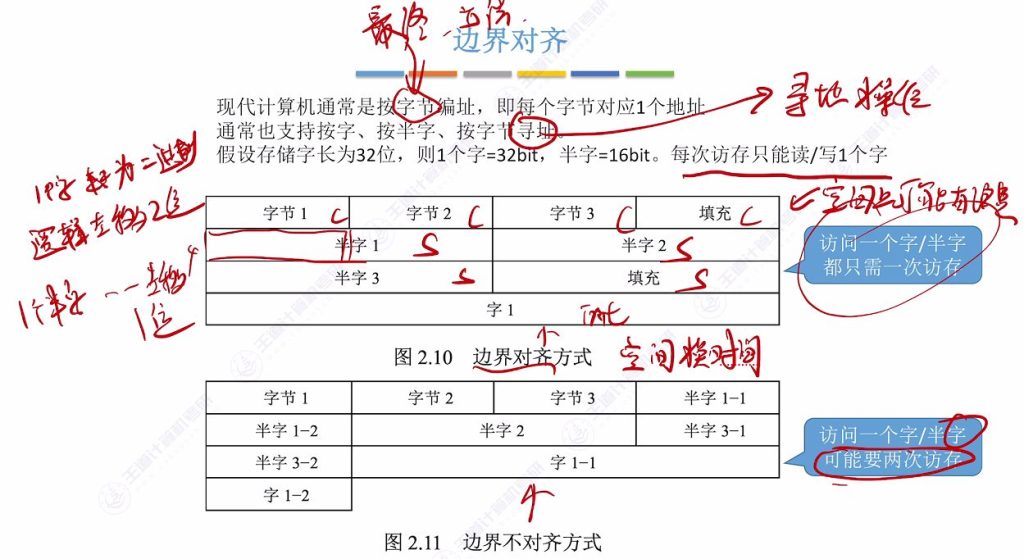
- 编址基础:
- 现代计算机按字节编址,每个字节对应唯一地址(如0,1,2,3…)
- 存储字长为32位时:1字=32bit=4字节,半字=16bit=2字节
- 寻址转换:
- 字地址→字节地址:逻辑左移2位
- 半字地址→字节地址:逻辑左移1位
- 存储策略对比:
- 边界对齐:牺牲部分存储空间(如char型后填充空白),保证数据单元完整存储在一个字内
- 优点:单次访存即可读取完整数据(如short型变量)
- 示例:结构体存储时主动填充空白字节
- 边界不对齐:充分利用所有存储空间,允许数据单元跨字存储
- 缺点:读取跨字数据需多次访存(如short型变量分存两个字中)
- 边界对齐:牺牲部分存储空间(如char型后填充空白),保证数据单元完整存储在一个字内
- 设计取舍:边界对齐采用空间换时间策略,虽然浪费存储空间,但显著提升访存效率
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


