一、数据的表示
1.1 进制转换
1)十进制与二进制
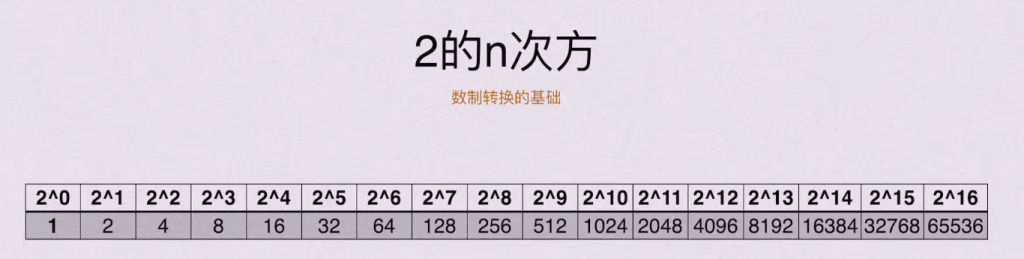


2)十进制与二进制

3)二进制与十六进制
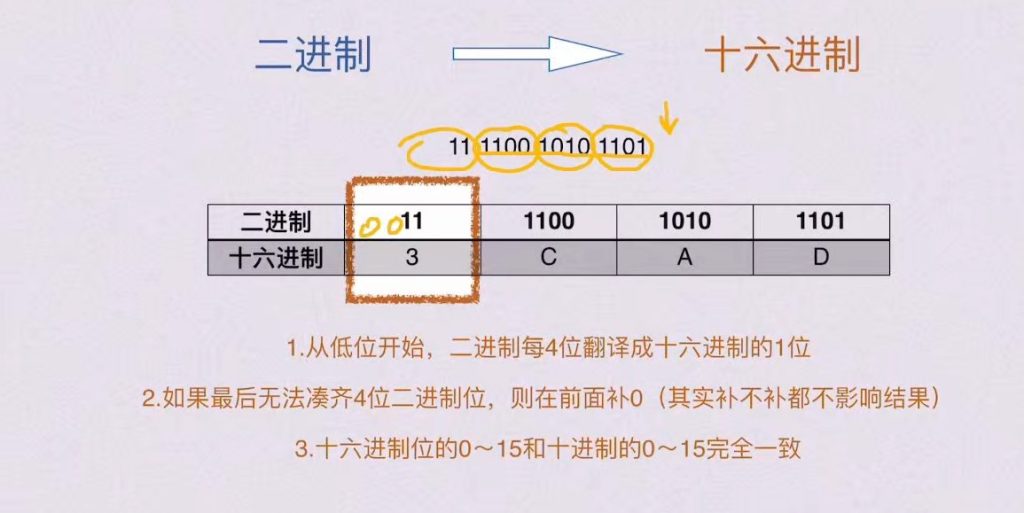
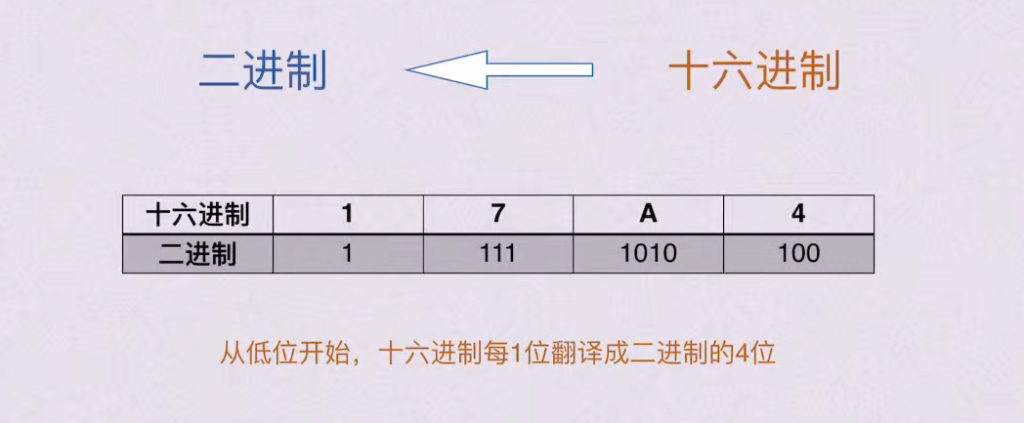
1.2 定点数与浮点数
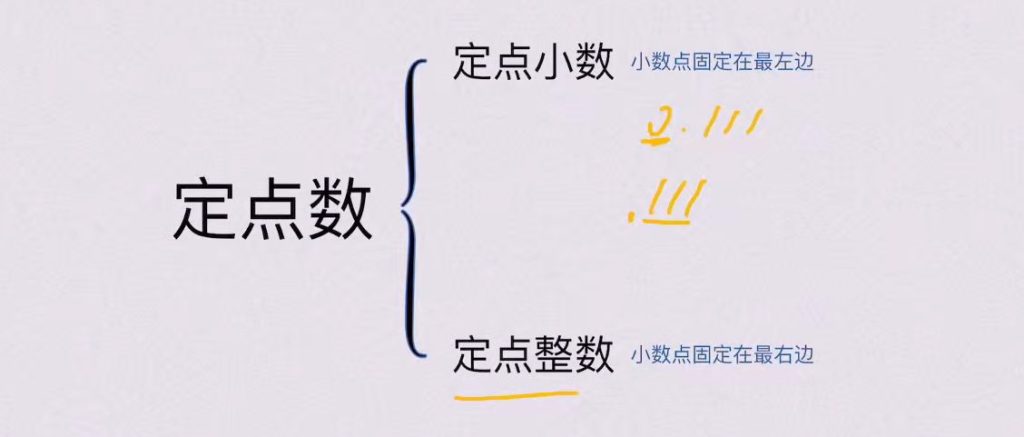
1)定点数
2)浮点数

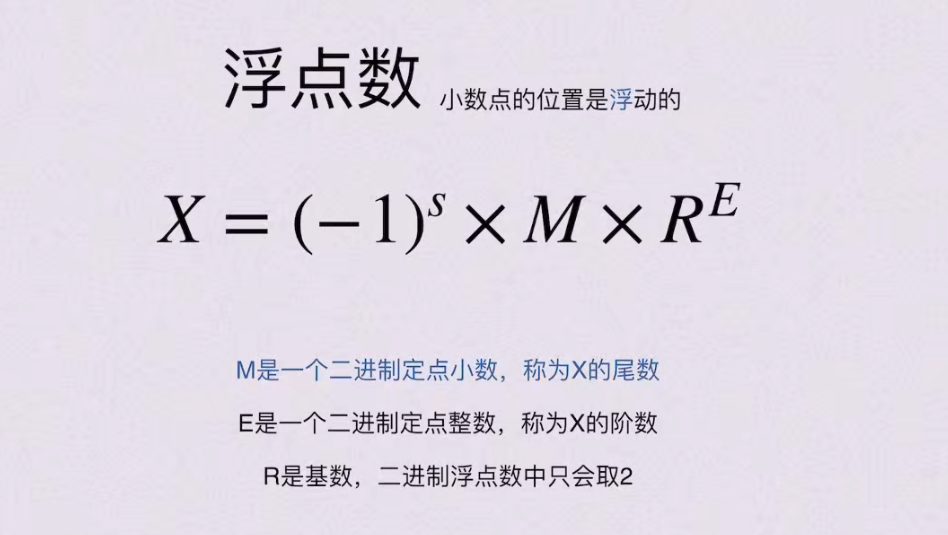


小数点右移3位,乘以10的-3
- 核心区别:定点数的小数点位置固定,浮点数的小数点位置浮动
- 类比说明:浮点数的”浮”体现在小数点可移动的特性,类似科学计数法的表示方式
1.3 定点数的编码表示

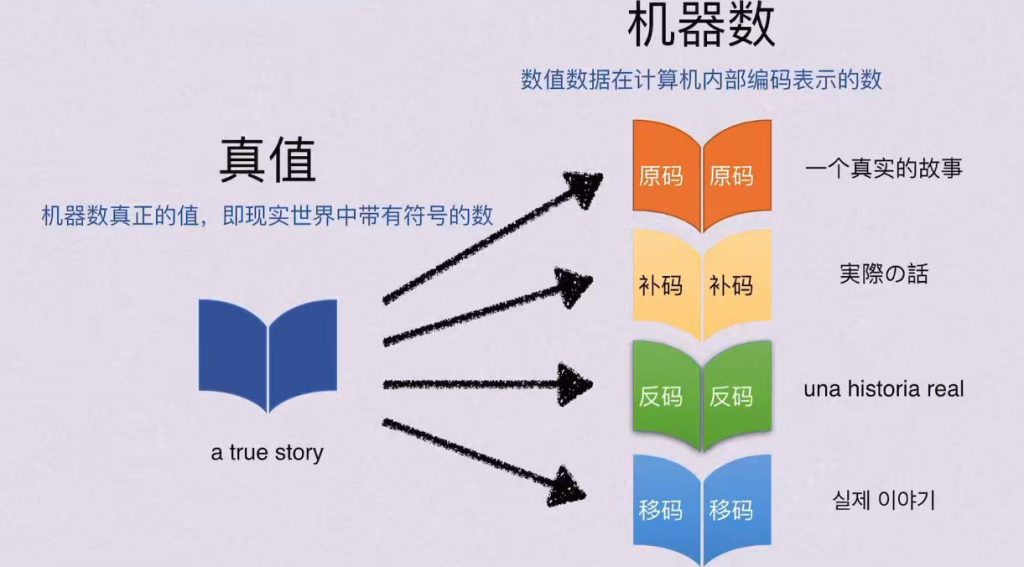
1)机器数和真值
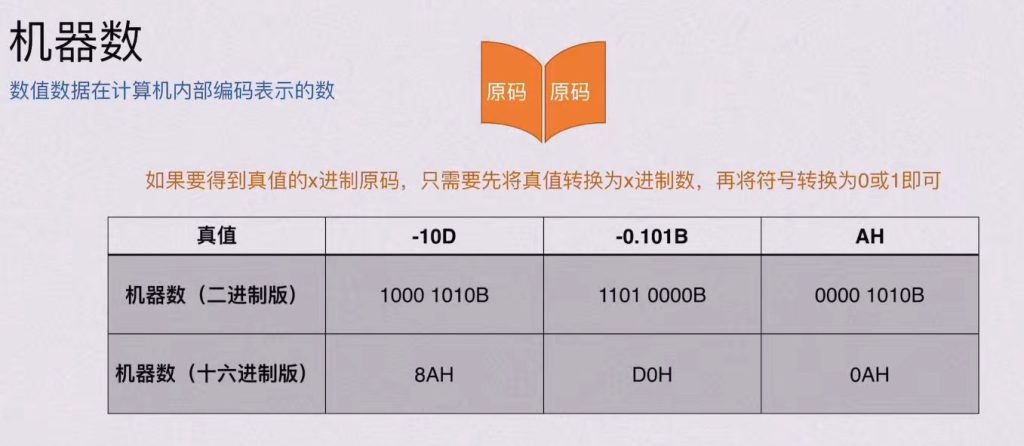
2)机器数的表示方式 – 原码
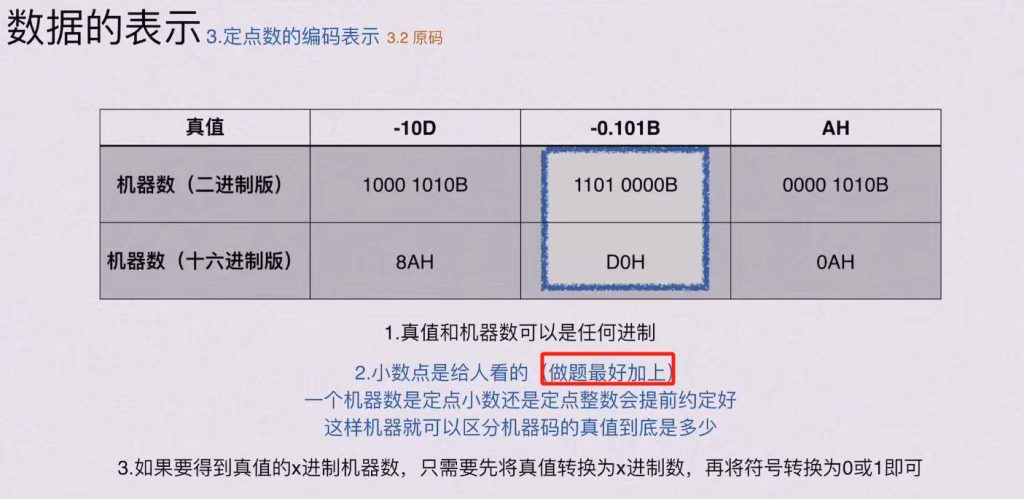

0有占用两种编码




1. 真值(True Value)
定义:数本身的 “实际值”,即日常生活中使用的带正负号的数值。
例子:温度为 +25℃,其中 “+25” 就是真值。
欠款 -100 元,其中 “-100” 就是真值。
2. 原码(Sign-Magnitude)
定义:计算机中表示带符号数的一种编码方式,规则为:最高位(符号位):0 表示正数,1 表示负数;
其余位:数值的绝对值的二进制表示。
例子(以 4 位二进制为例):真值 +5 → 原码 0101(符号位 0,数值部分 101=5)。
真值 -5 → 原码 1101(符号位 1,数值部分 101=5)。
3. 机器数(Machine Number)
定义:计算机内部存储、运算时使用的二进制编码。原码、反码、补码都是机器数的不同形式。
例子:原码:+5 → 0101,-5 → 1101。
补码(另一种机器数):+5 → 0101,-5 → 1011(补码的计算涉及反码 + 1)。
三者关系总结
真值是现实中的数值(如 + 5、-5)。
原码是机器数的一种,直接用符号位 + 绝对值表示真值。
机器数是计算机实际存储的编码,可能采用原码、补码等形式(补码更常用,因为便于加减运算)。
简单理解:真值是 “人话”,原码是 “机器的一种翻译方式”,机器数是 “机器内部的表示统称”。
3)机器数的表示方式 – 反码
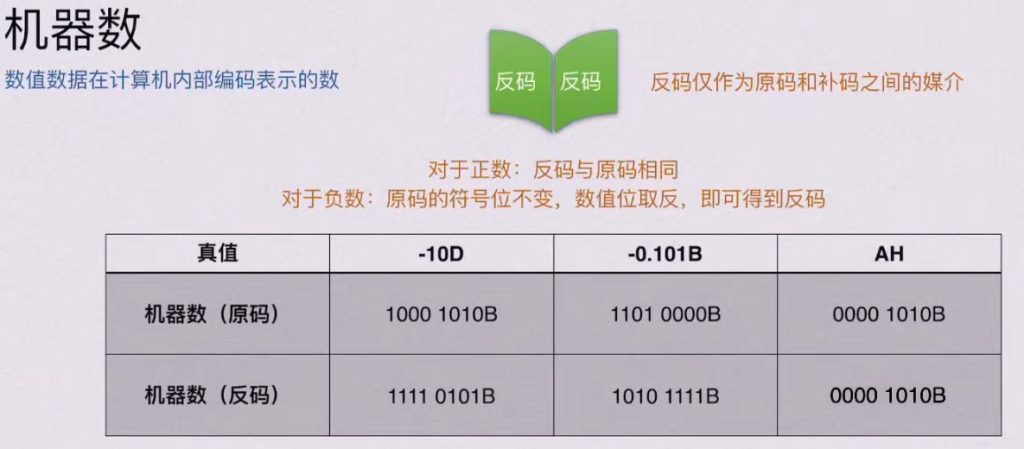
4)机器数的表示方式 – 补码
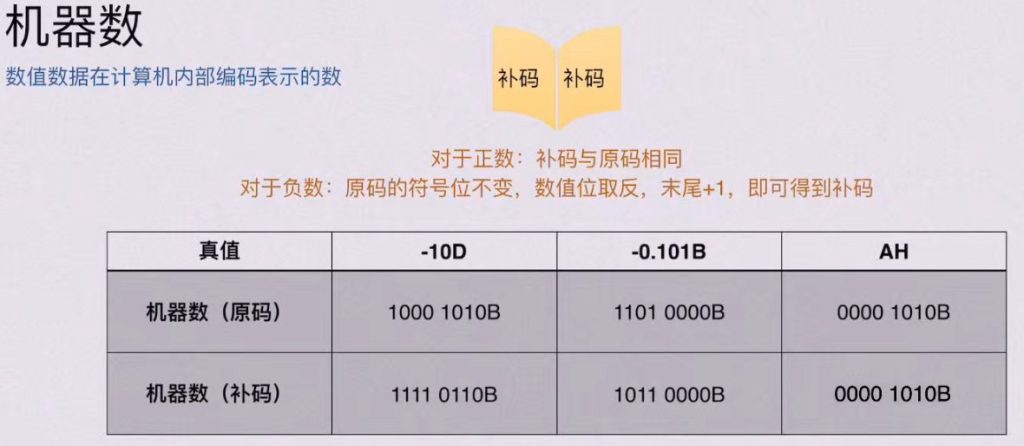
5)补码转真值(简便方法)

简便方法

6)补码表示范围

7)原码、补码范围区别
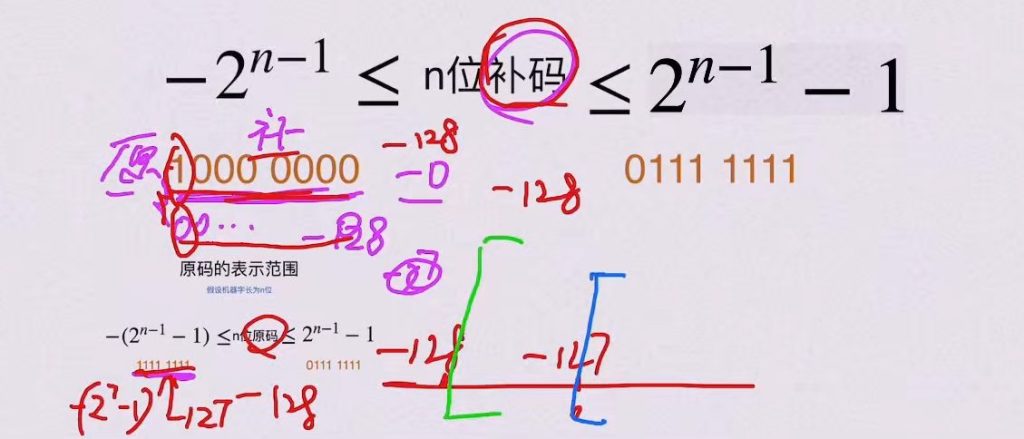
- 补码与原码表示范围的对比
- 关键差异:
- 补码比原码多表示一个负数(如8位补码可表示-128,原码只能到-127)
- 原因:补码将原码的”-0″编码重新解释为最小负数
- 表示效率:
- 补码:2n个编码表示2n个不同数值
- 原码:2n个编码只能表示2n−1个不同数值(因零占两个编码)
- 关键差异:

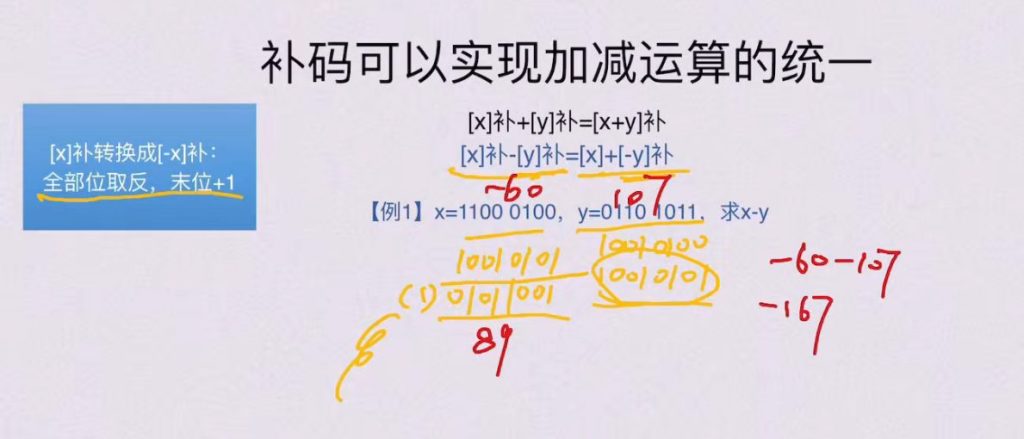
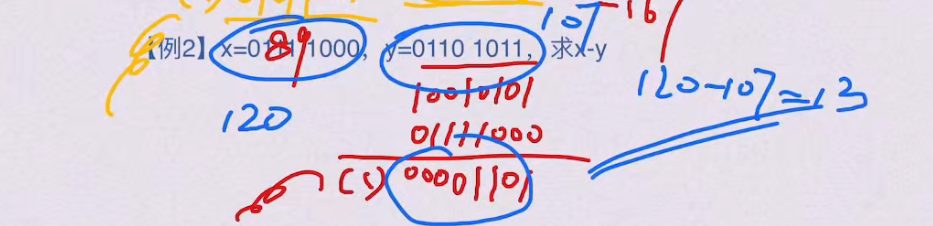
1.4 补码可以实现加减运算的统一

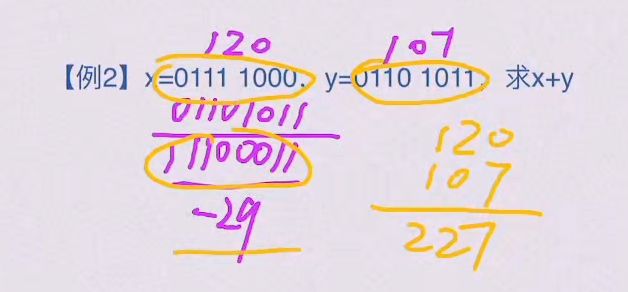



1.5 无符号数
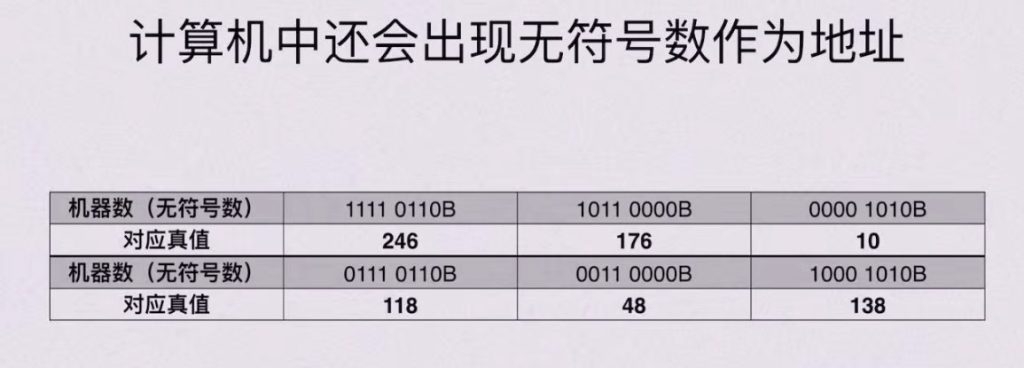

1.6 移码
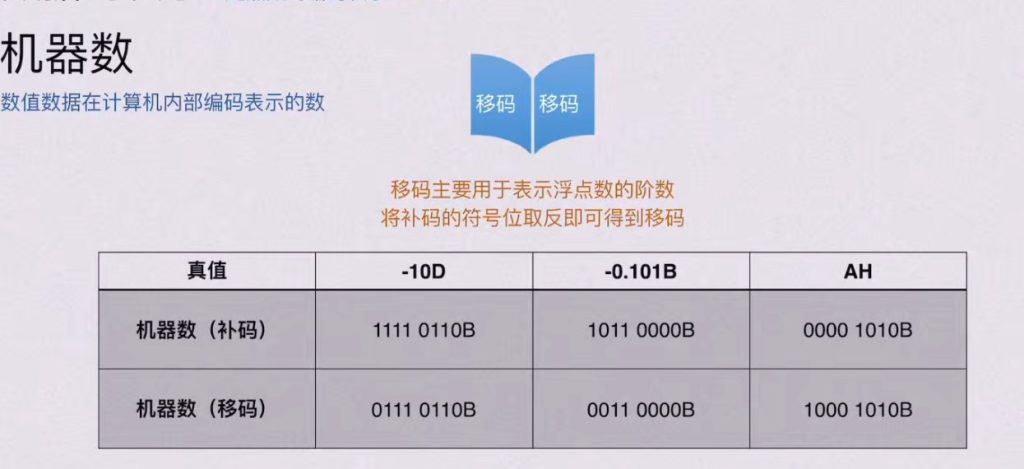
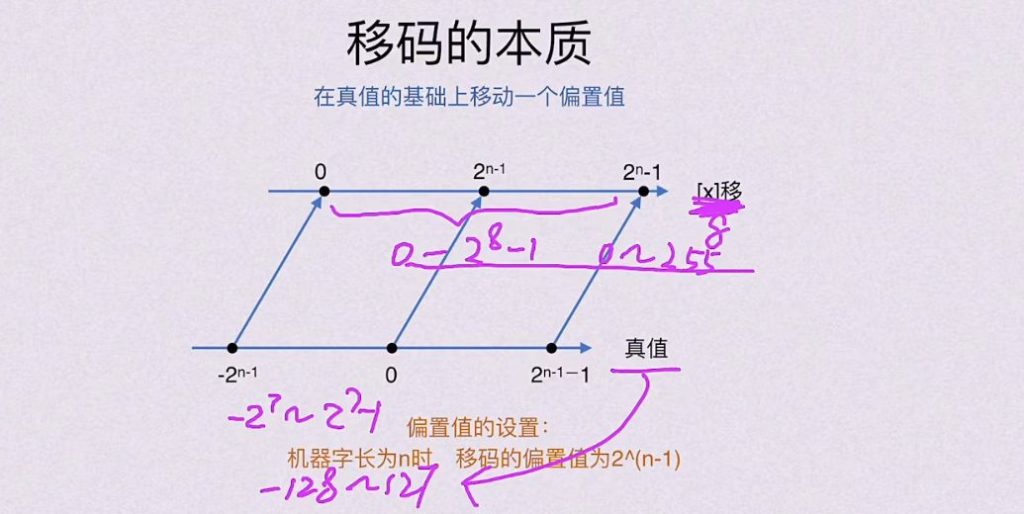
移码的核心作用是方便比较带符号数的大小,尤其适合表示浮点数的 “阶码”(指数部分)。
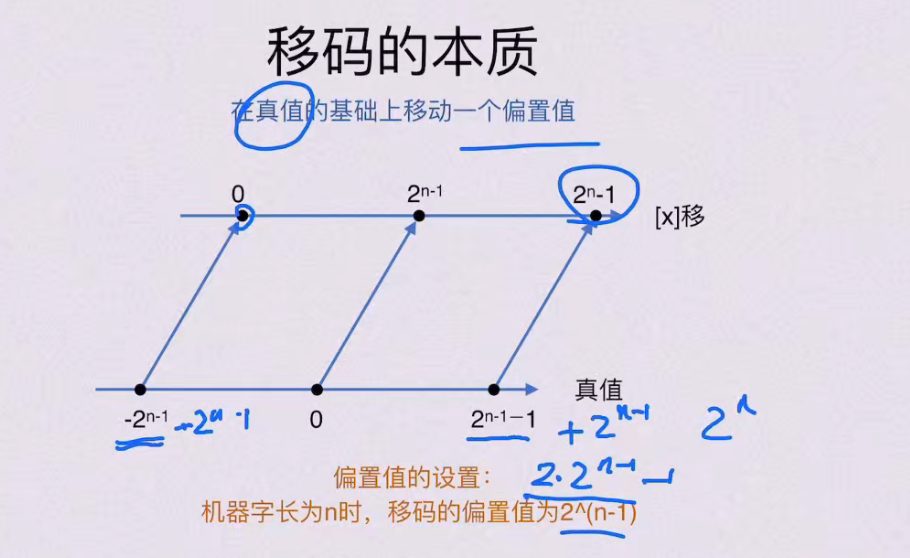
简单理解:
移码的本质是给所有数加一个 “偏移量”,把原本有正有负的数 “整体上移”,变成非负数。这样一来,移码的二进制大小顺序和真值的大小顺序完全一致—— 直接比较移码的二进制,就能知道原来的数谁大谁小,不需要额外处理符号位,极大简化了计算机的比较逻辑。
举例(以 4 位二进制为例,偏移量取 8,即 2³):
移码的计算规则:移码 = 真值 + 偏移量(这里是 8)
| 真值 | 移码(真值 + 8) | 二进制移码 |
|---|---|---|
| -4 | -4 + 8 = 4 | 0100 |
| 0 | 0 + 8 = 8 | 1000 |
| 3 | 3 + 8 = 11 | 1011 |
| 5 | 5 + 8 = 13 | 1101 |
观察规律:
- 真值越大,移码的二进制数值也越大(1101>1011>1000>0100,对应 5>3>0>-4)。
- 计算机只需像比较无符号数一样比较移码的二进制,就能直接判断真值的大小,不需要考虑符号位的干扰。
实际用途:
浮点数由 “阶码”(指数)和 “尾数”(有效数字)组成,阶码的大小决定了浮点数的整体大小。移码因为能直接比较大小,被广泛用于表示浮点数的阶码,让计算机快速判断两个浮点数的大小关系(比如比较 1.2×10³ 和 3.4×10²,只需比较阶码 3 和 2 的移码大小)。
1.7 练习



1.8 数据的宽度和存储
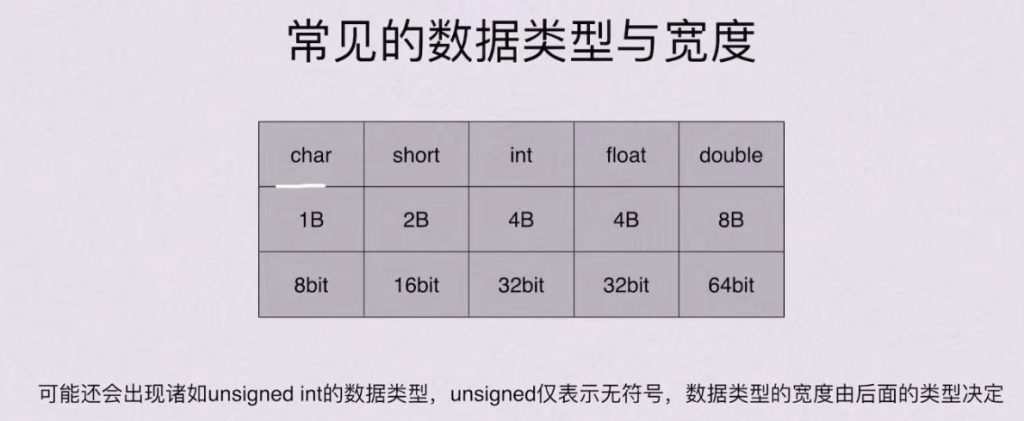
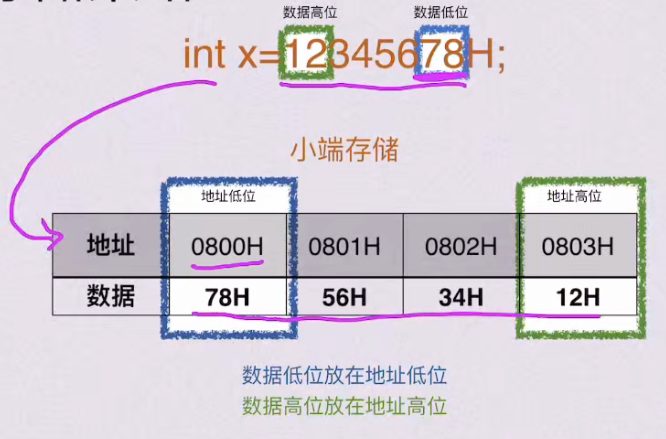
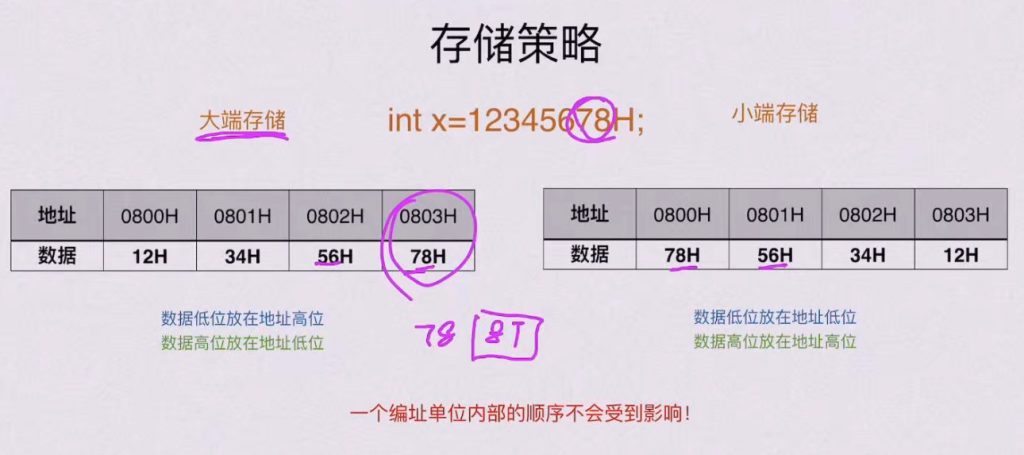
1.9 大小端存储
大端存储
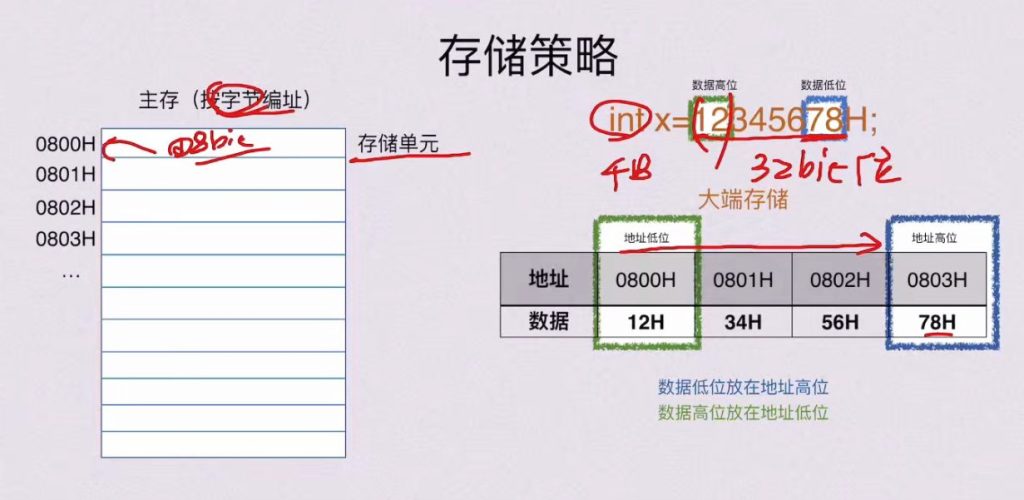
小端存储
二、运算部件
2.1 加法器
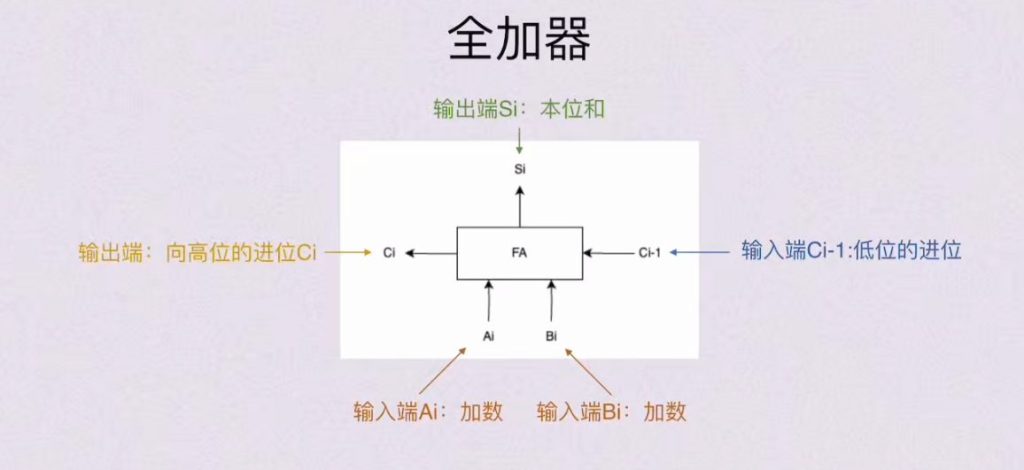
2.1.1 全加器
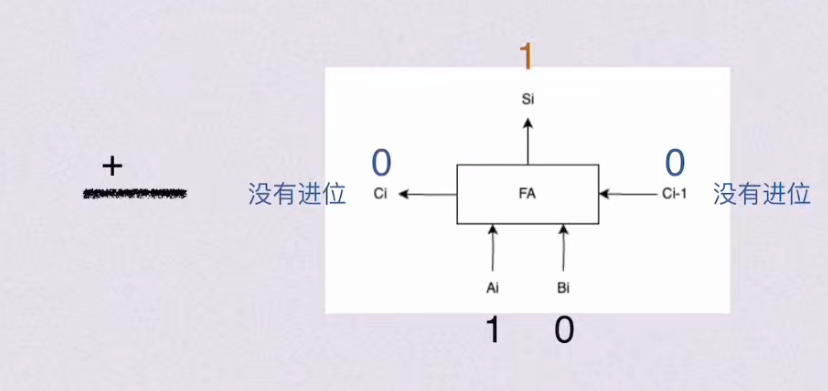
2.1.2 串行进行加法器
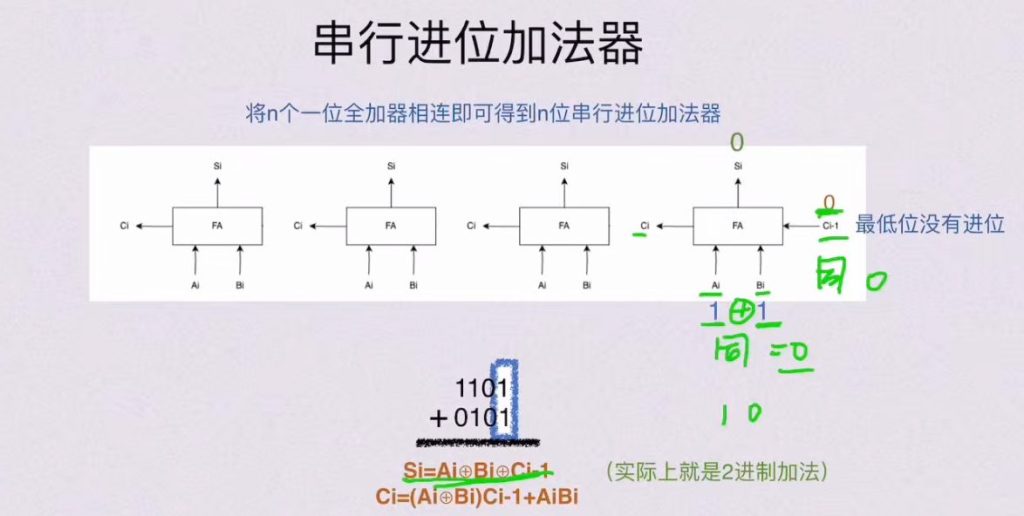
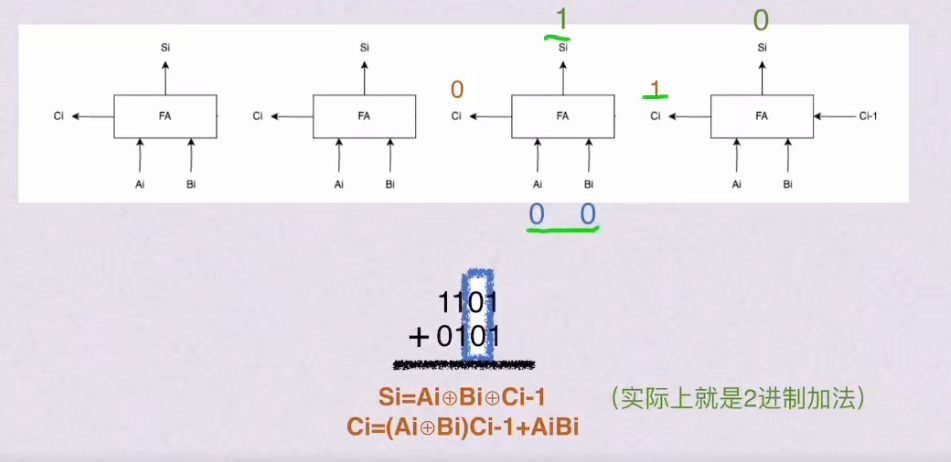
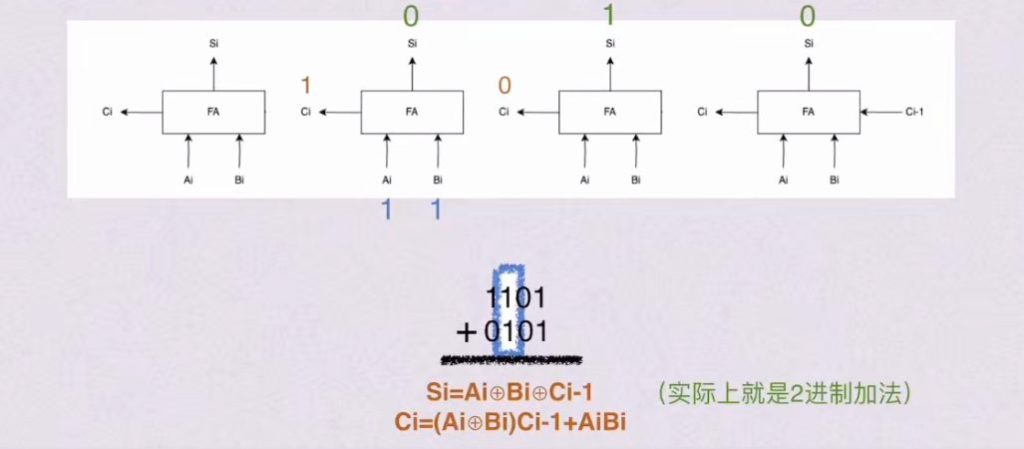
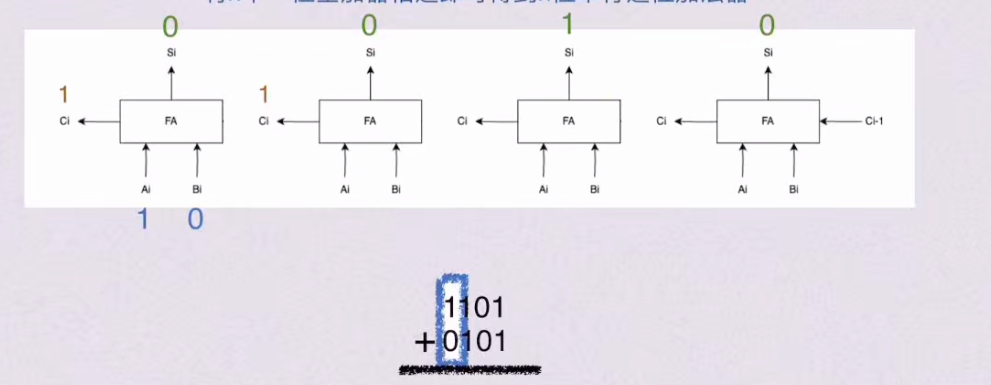
- 最高位的进位直接丢弃(不是溢出)
缺陷
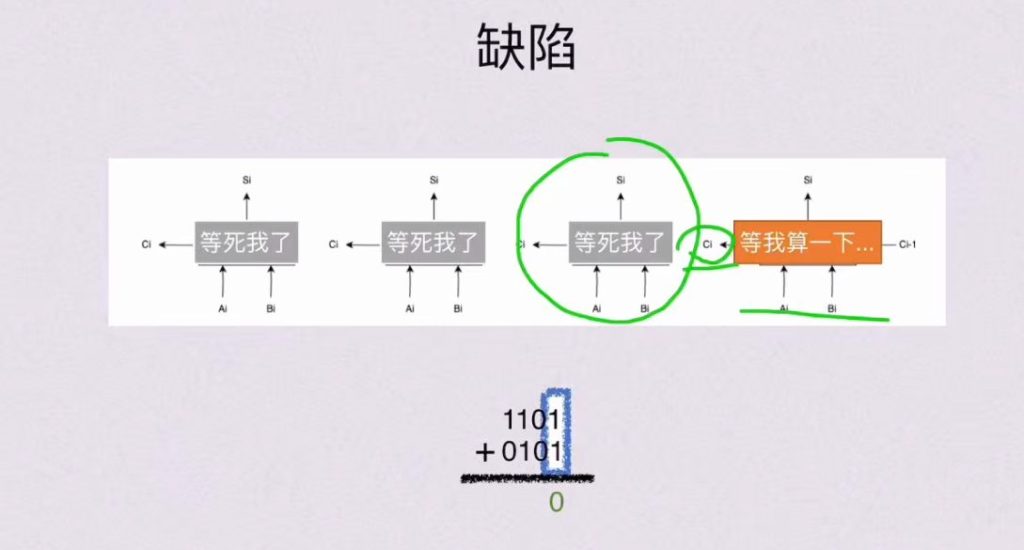
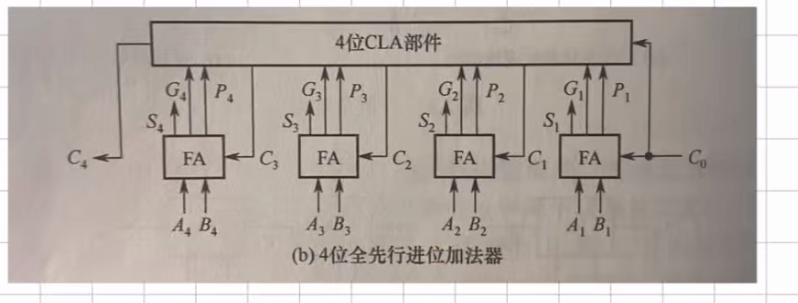
2.1.3 并行进行加法器

串行进位加法器进位推导
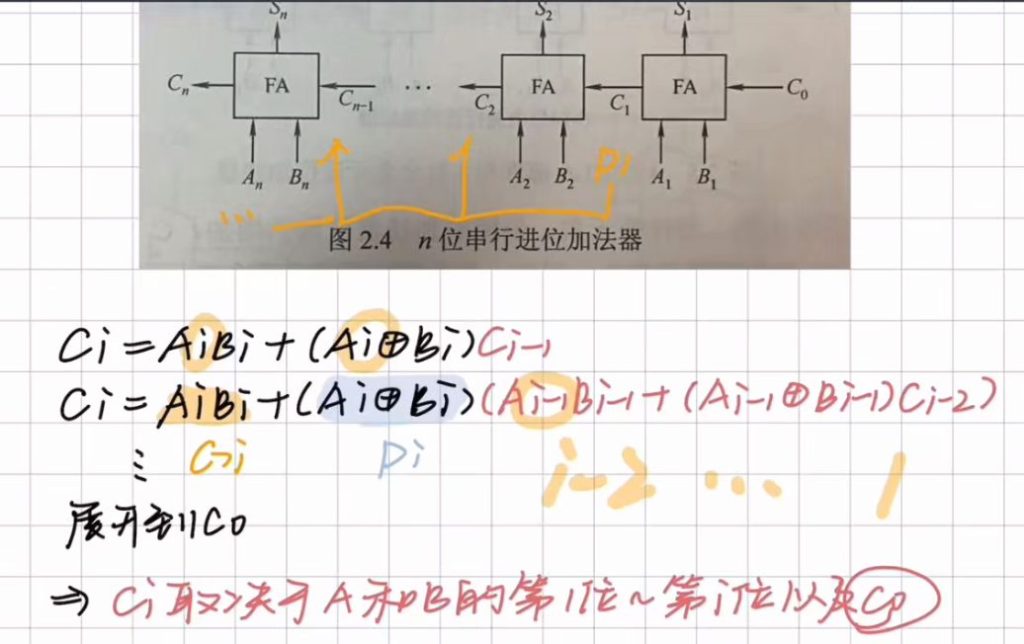

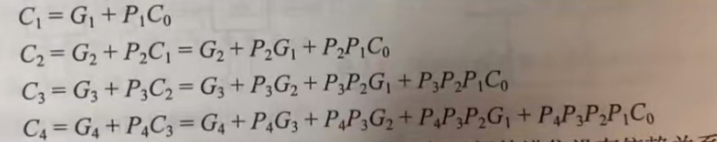
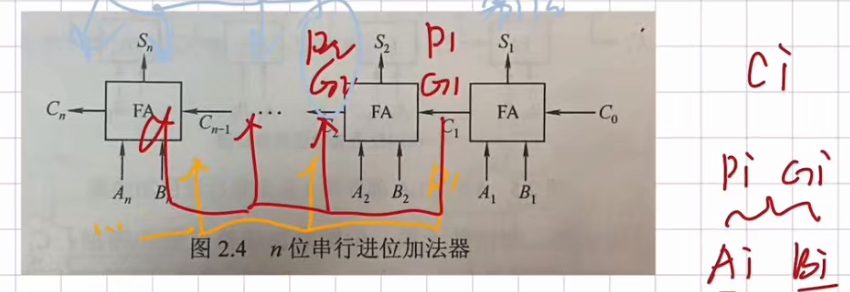
并位加法器
2.1.4 带标志加法器(大题重点)
OF 仅对带符号数有效,题目如果问,按表达式推
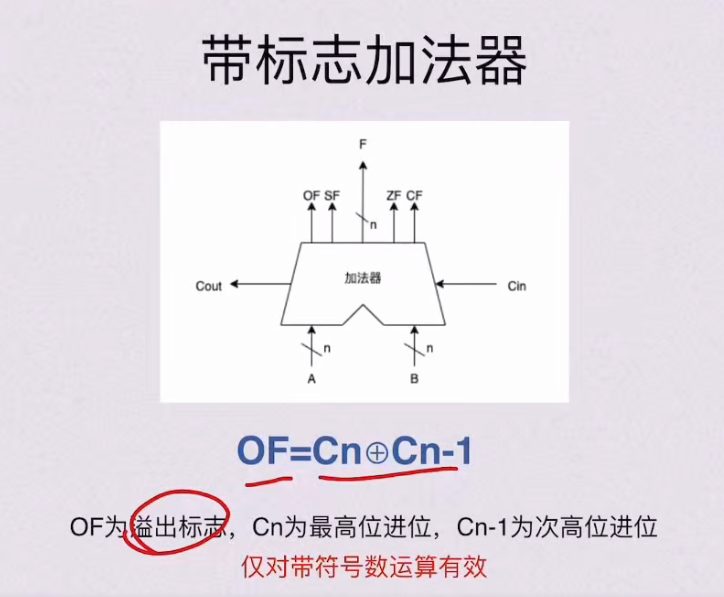

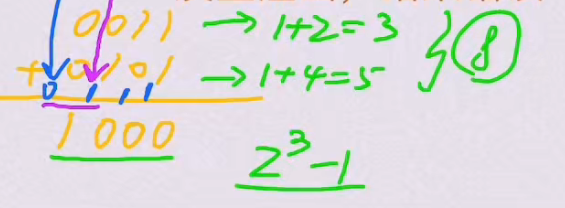
SF
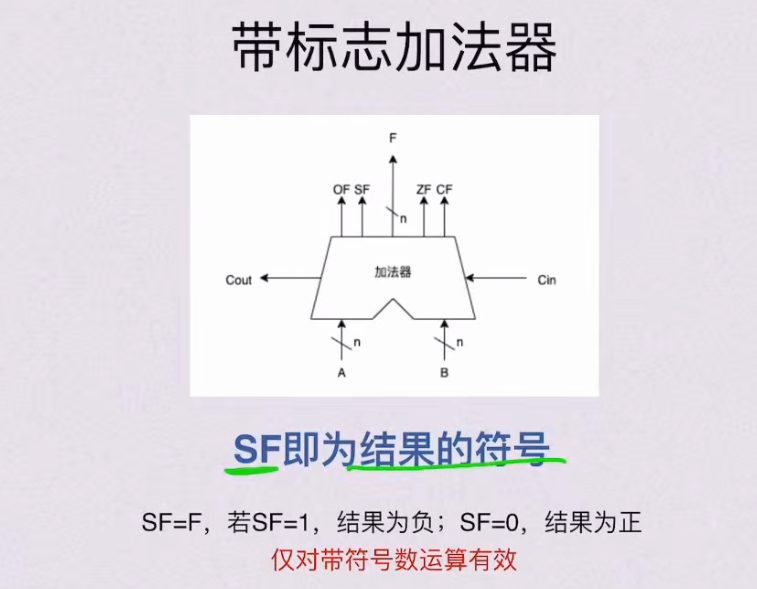
ZF
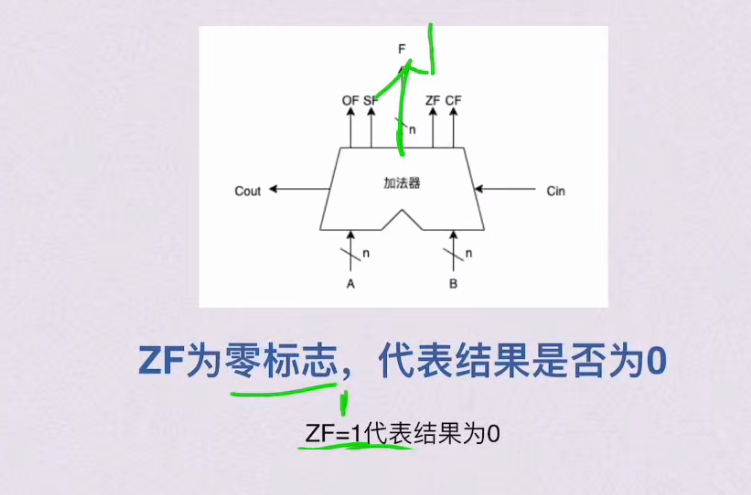
CF – 仅对无符号数有效
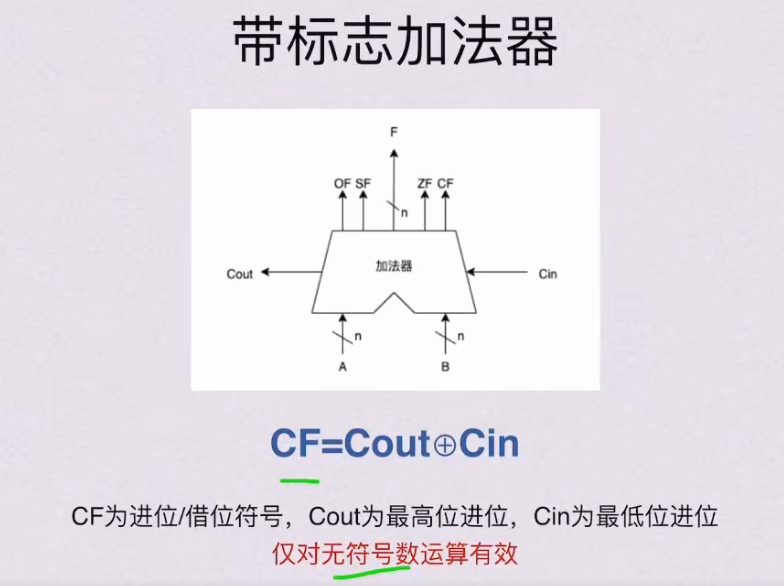


2.2 算数逻辑单元ALU
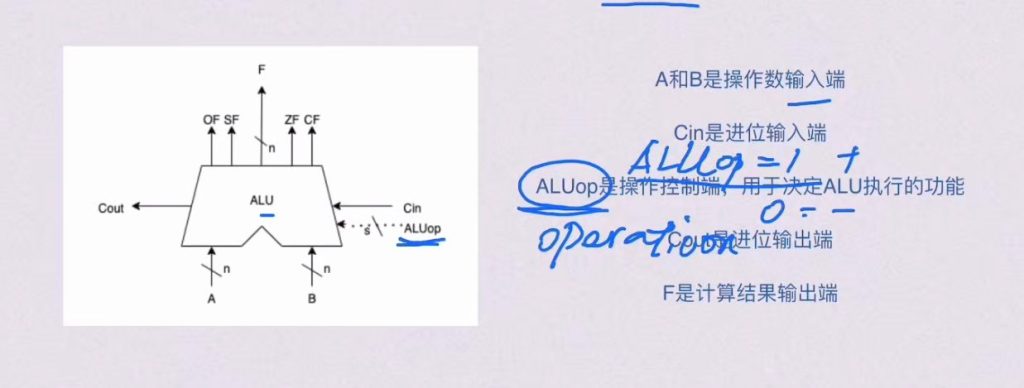
ALUop = 1 加法; ALUop = 0 减法
三、符号扩展与零扩展
3.1 符号扩展的原则


3.2 符号扩展的应用
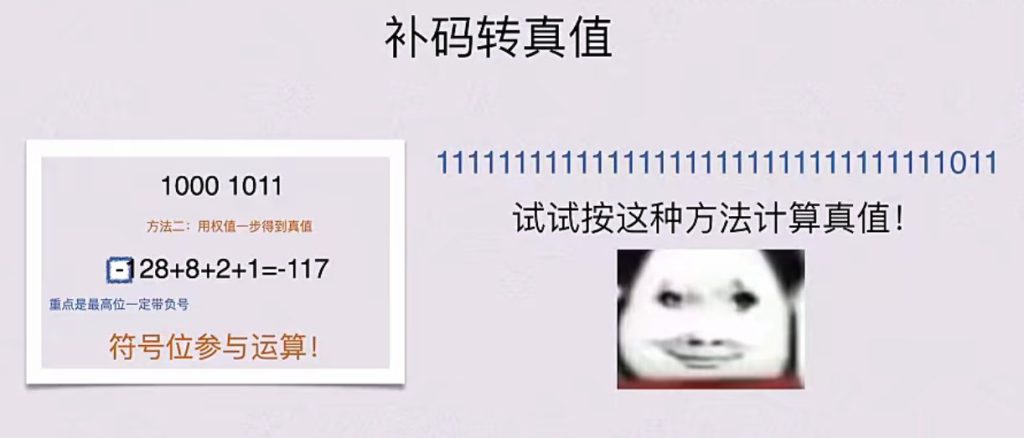
补码转真值


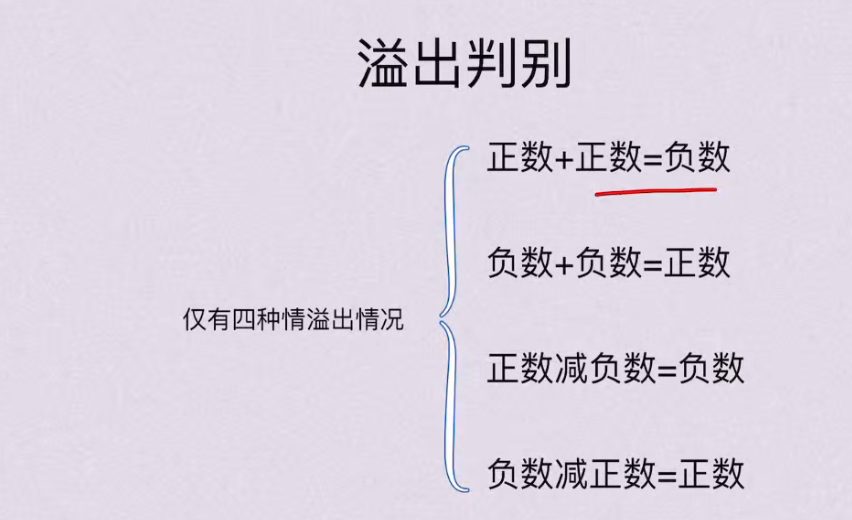
溢出判断

没有发生溢出

发生溢出
3.3 零扩展

四、定点数的运算(不是考察重点)
4.1 定点数的移位操作
4.1.1 左移
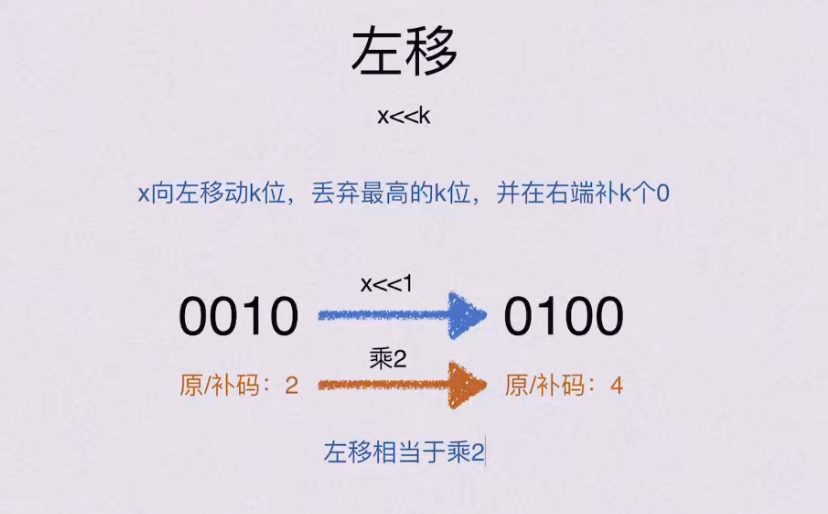
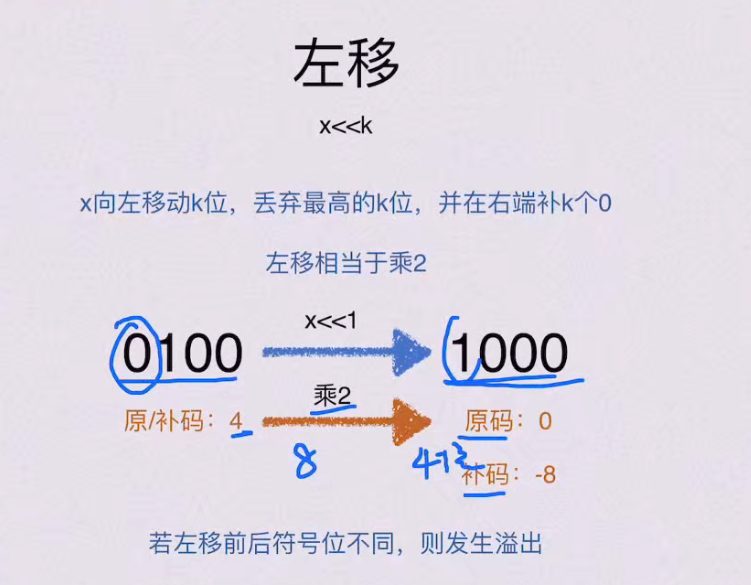
4.1.2 右移
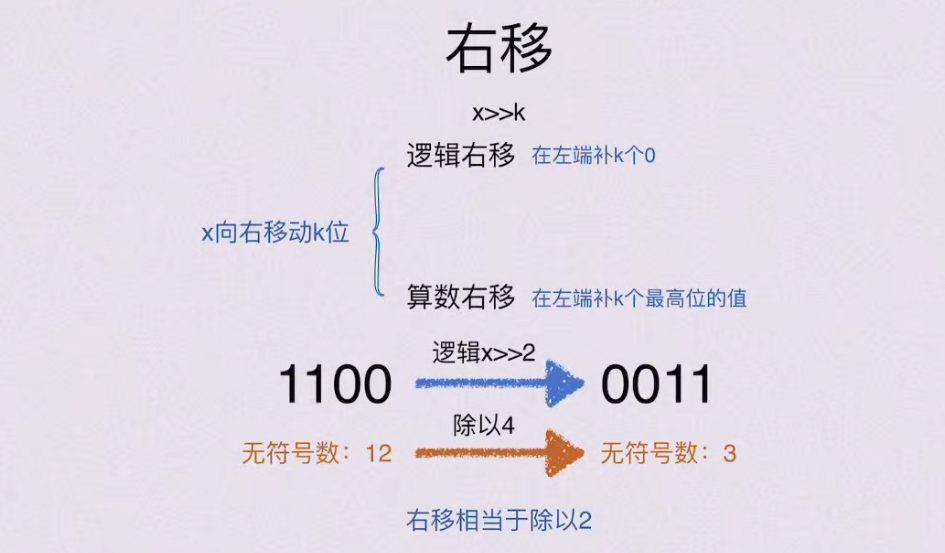
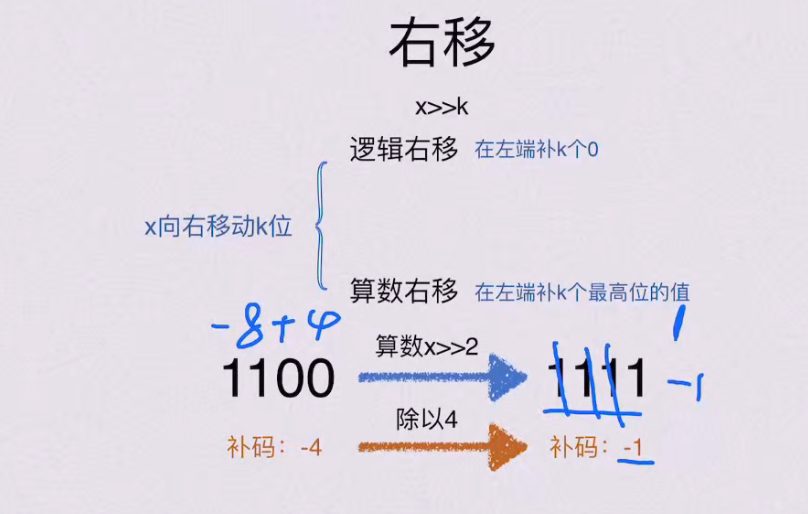
算数右移 针对 补码,逻辑右移用于无符号数
4.2 补码的加减运算
4.2.1 补码加减运算法则

4.2.2 补码加减运算电路
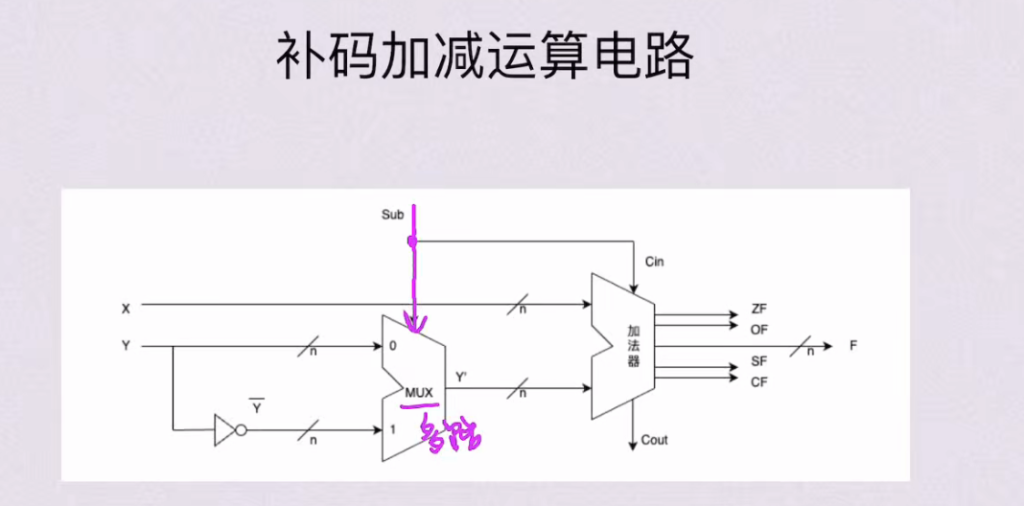
[y]补 -> [-y]补
1、全部按位取反
2、末位 + 1
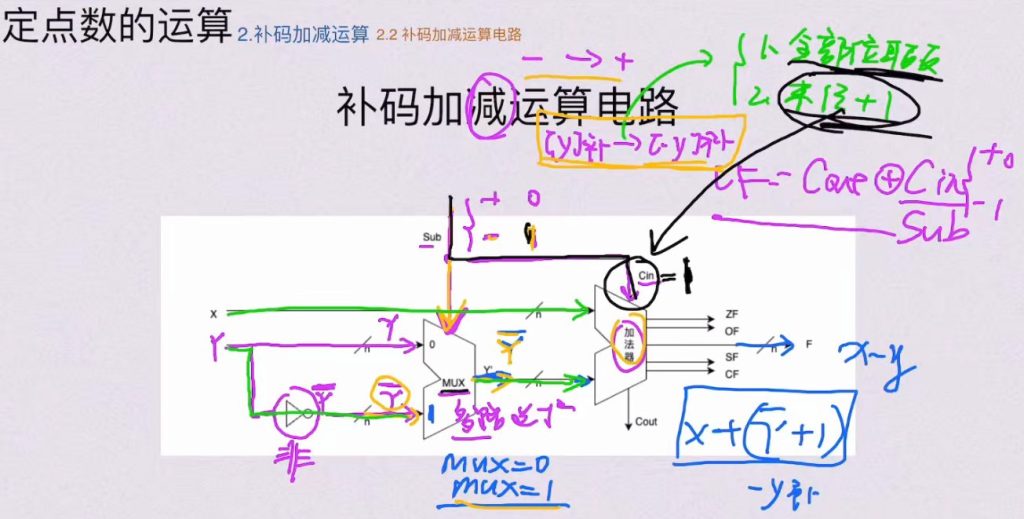
- 核心组件:
- 带标志加法器:执行实际加法运算
- 多路选择器(MUX):选择输入y或y取反
- 控制信号Sub:决定执行加法(0)或减法(1)
- 减法实现原理:
- Sub=1时:MUX输出y取反,同时Cin=1
- 等效操作:y取反加1得到−y补码
- 加法实现原理:
- Sub=0时:MUX直接输出y,Cin=0
- 等效操作:直接计算x+y
- 标志位应用:
- OF:有符号数溢出标志
- CF:无符号数进位标志
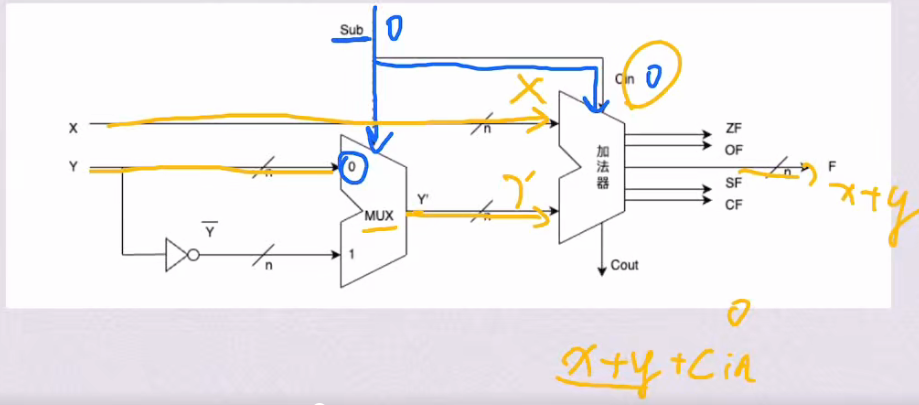
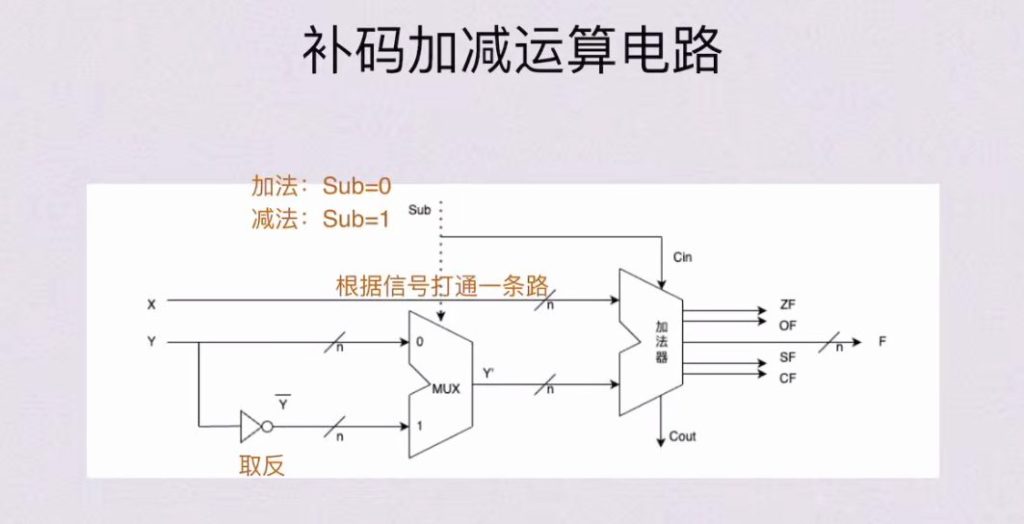
该图需要记忆
4.2.3 溢出判别
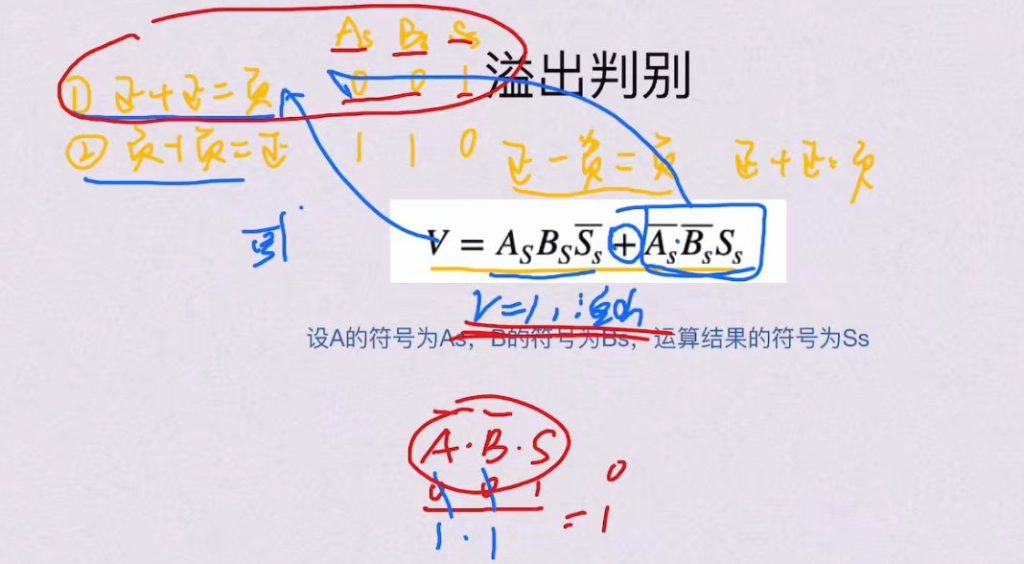


4.3 乘法原理和电路
4.3.1 原码乘法

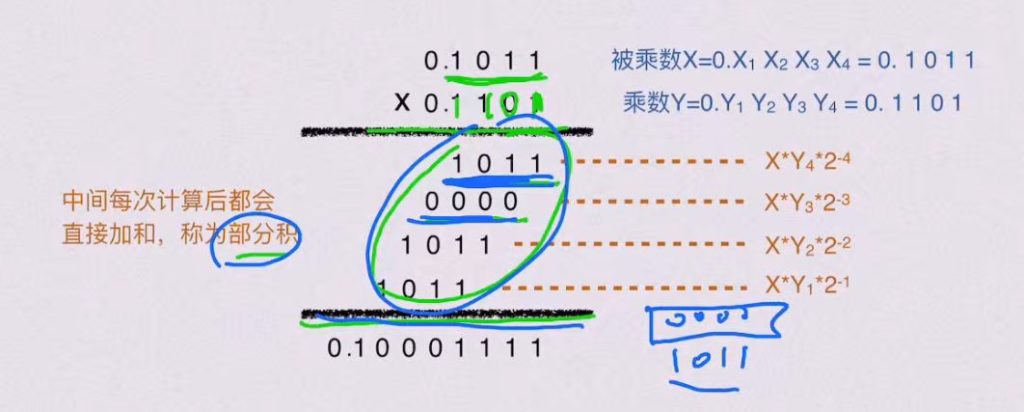
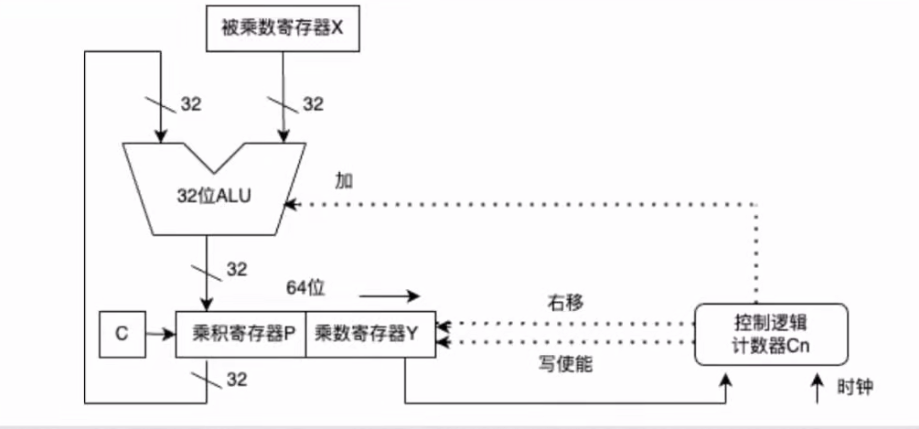
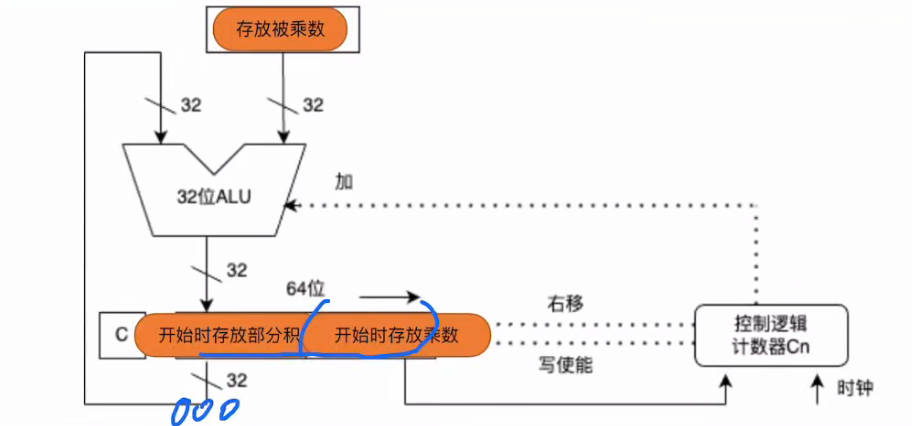
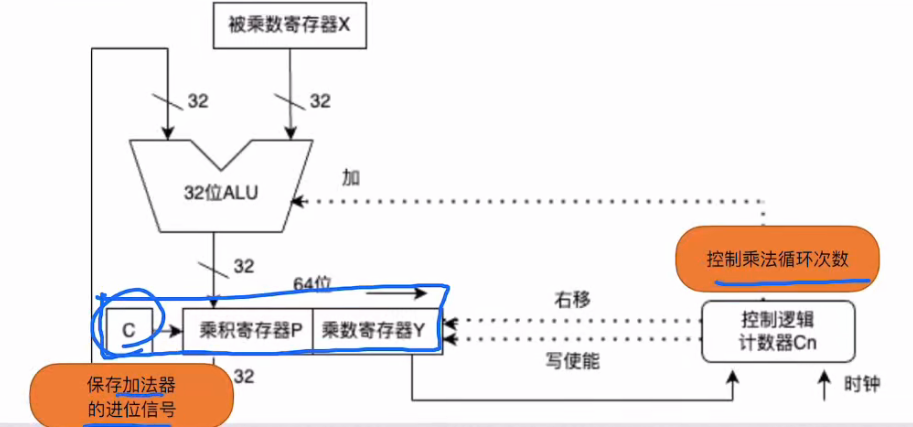
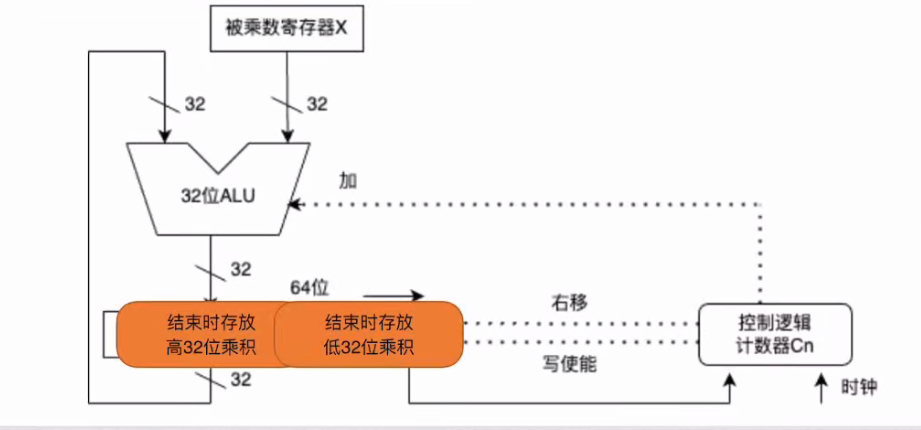


4.3.2 补码乘法
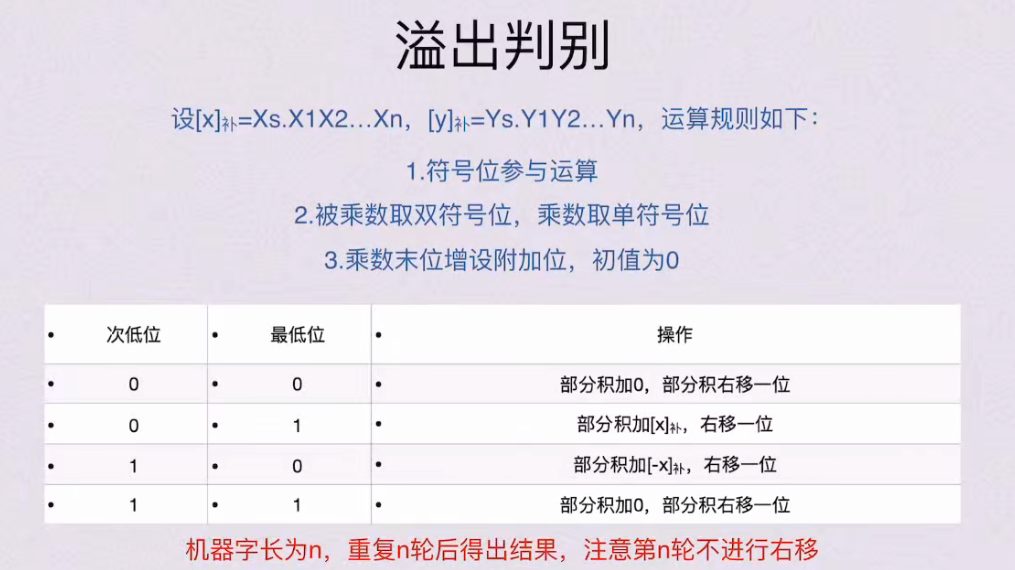
4.4 除法原理与电路
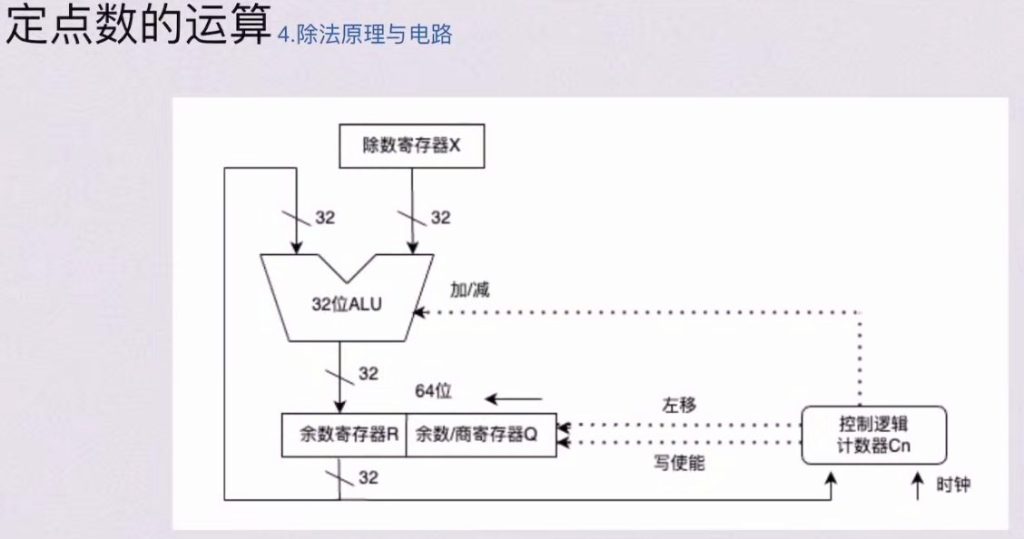
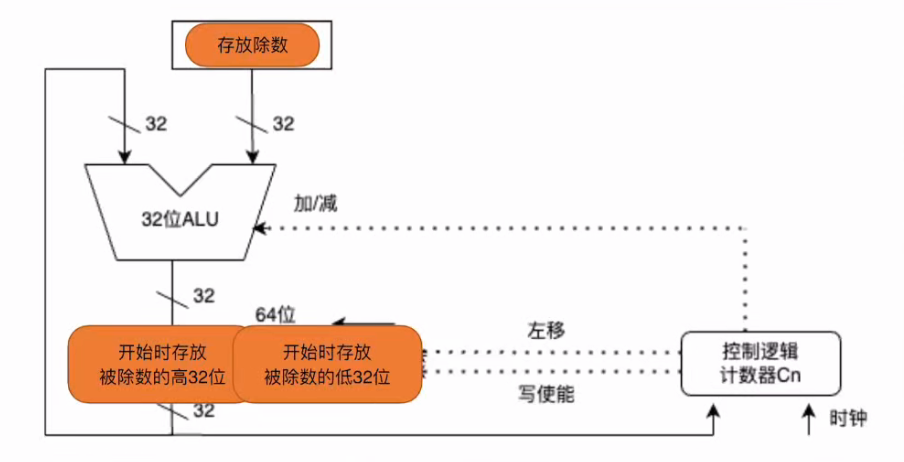
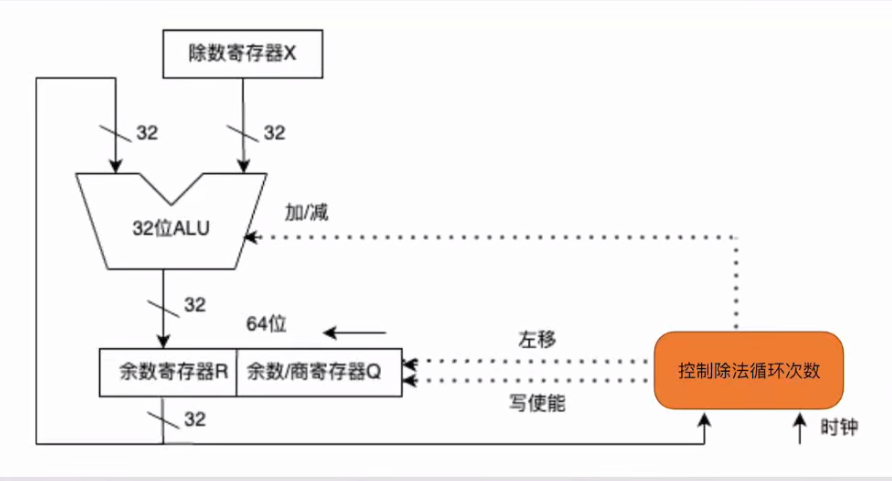
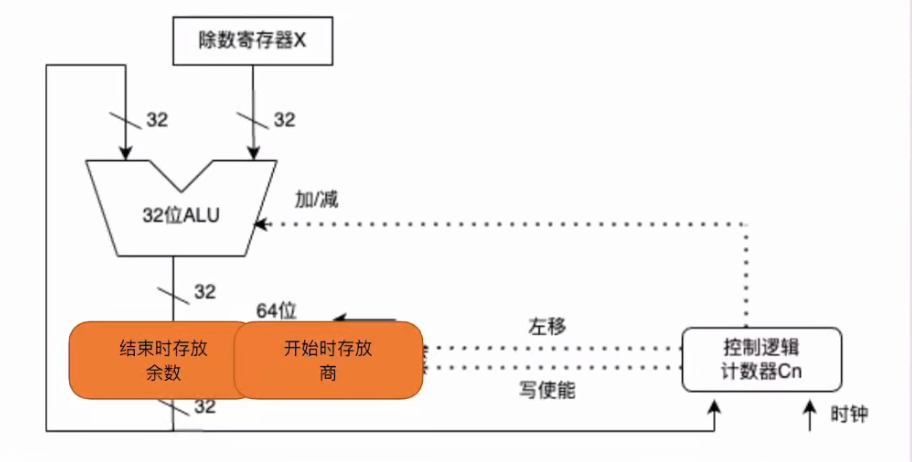

五、浮点数与IEEE754
5.1 浮点数
5.1.1 浮点数的表示格式

【注】:基数一般是考察2这种情况
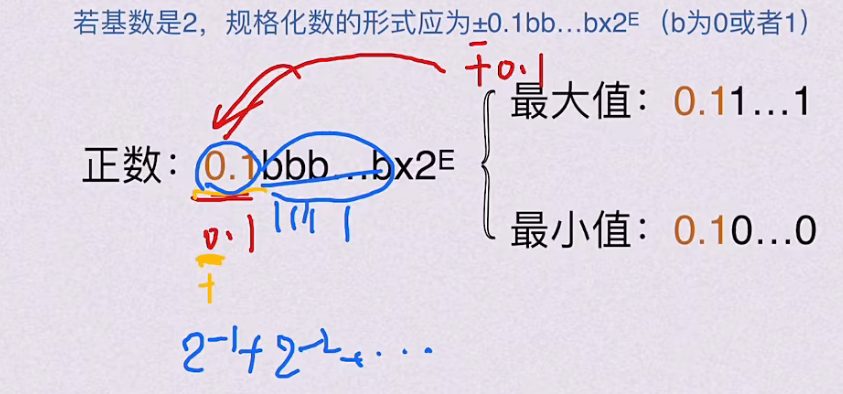
5.1.2 浮点数的规格化


正数
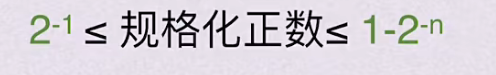
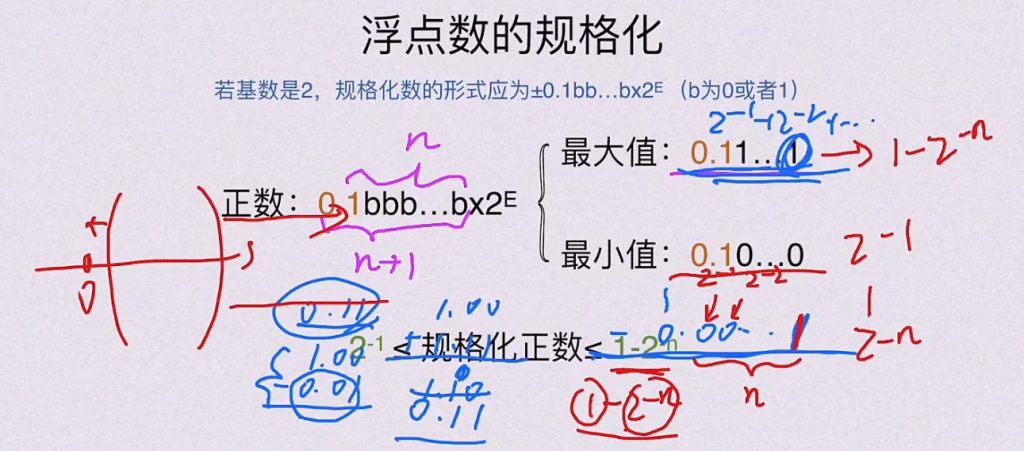
负数


- 规格化
- 基数r=2时:
- 形式:±0.1bb…b×2^E(b为0或1)
- 关键特征:小数点后第一位必须为1(二进制有效位)
- 基数r=2^n时:
- 要求:尾数最高n位不全为0
- 本质:尾数绝对值必须大于r分之一(如r=4时需>0.25)
- 原码特性:
- 尾数用原码表示时,真值范围在(-1,1)之间
- 因此规格化形式中整数部分只能是0(正数)或符号位(负数)
- 基数r=2时:

5.1.3 规格化操作(区别IEEE754)



5.1.4 浮点数的加减运算






5.1.5 补码表示的尾数

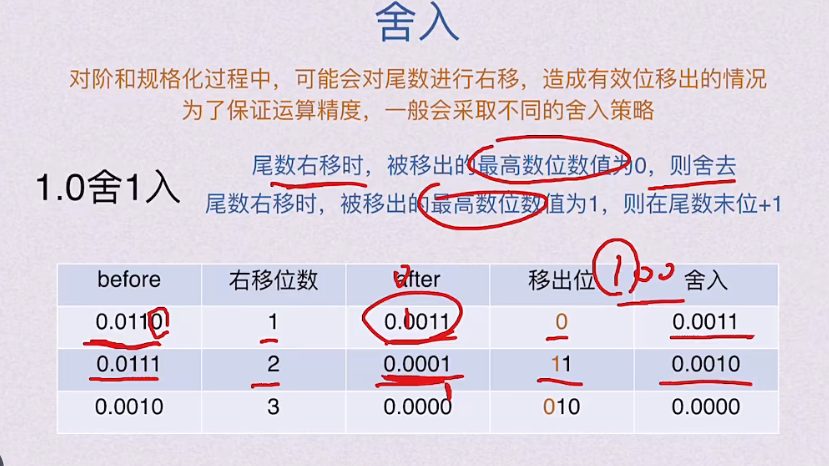
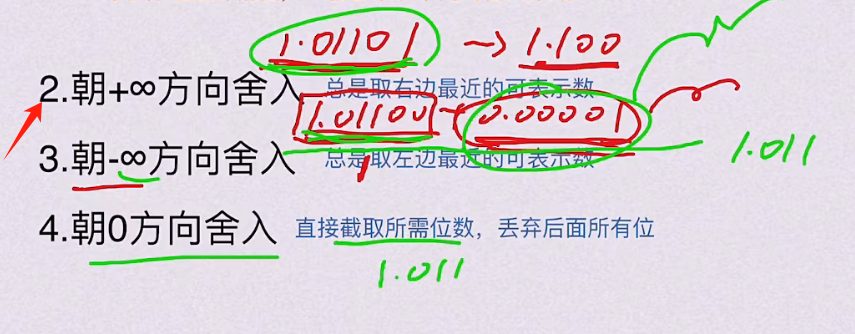
5.1.6 舍入
5.2 IEEE754
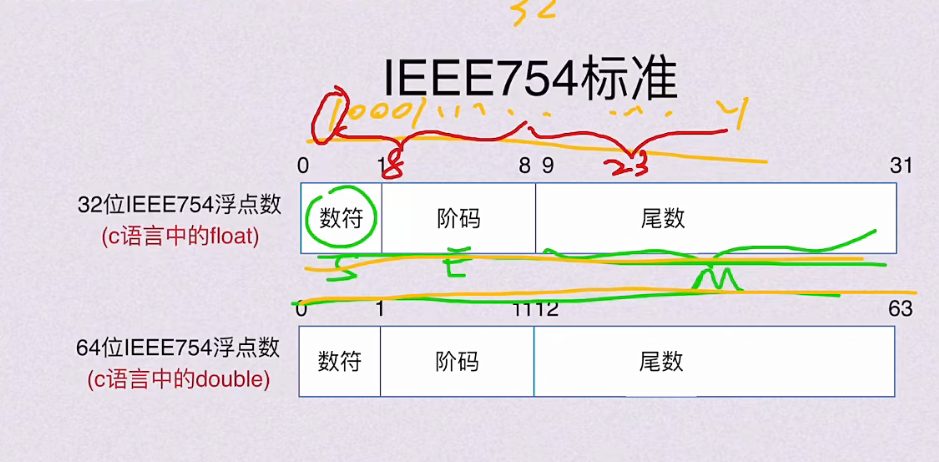
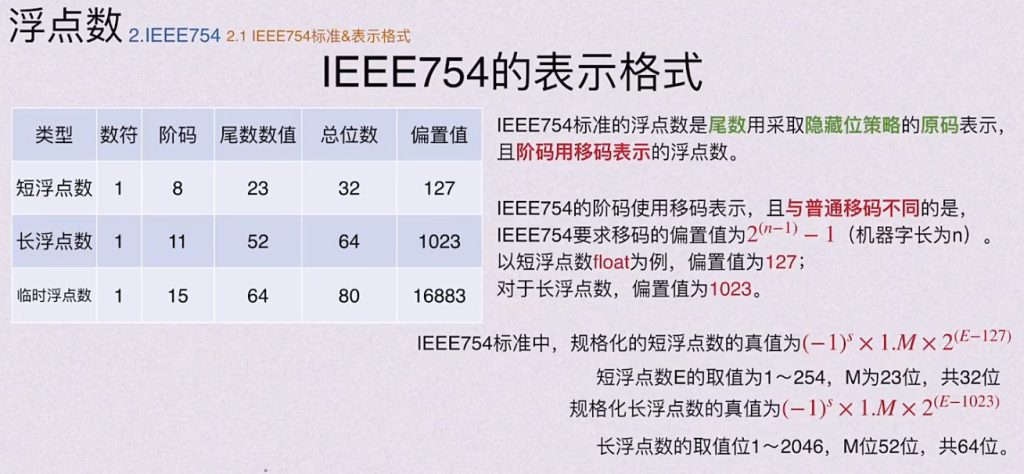
5.2.1 IEEE754标准 & 表示格式
5.2.2 移码
5.2.3 IEEE754浮点数规格化

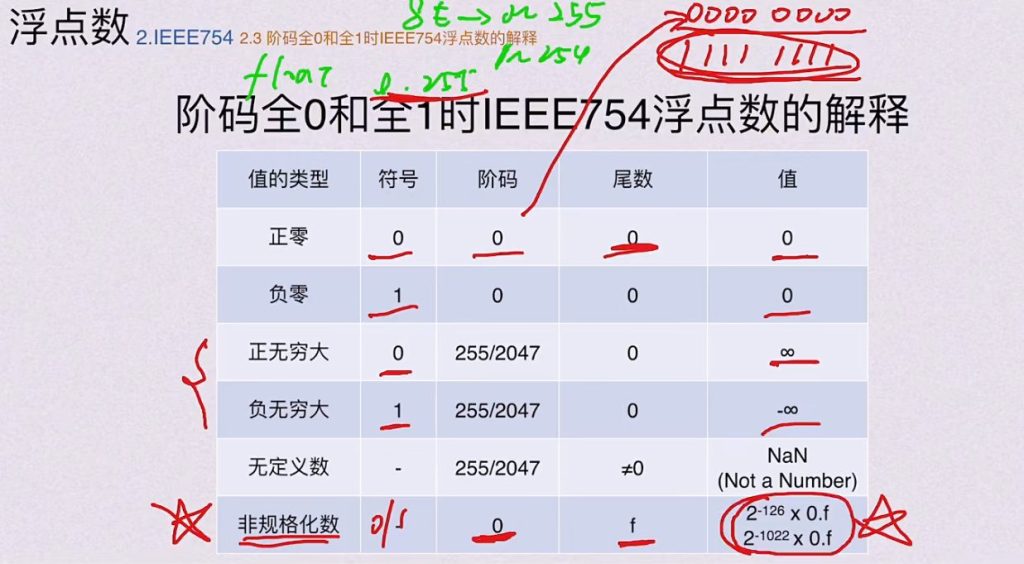
5.2.4 阶码全0和全1时IEEE754浮点数的解释
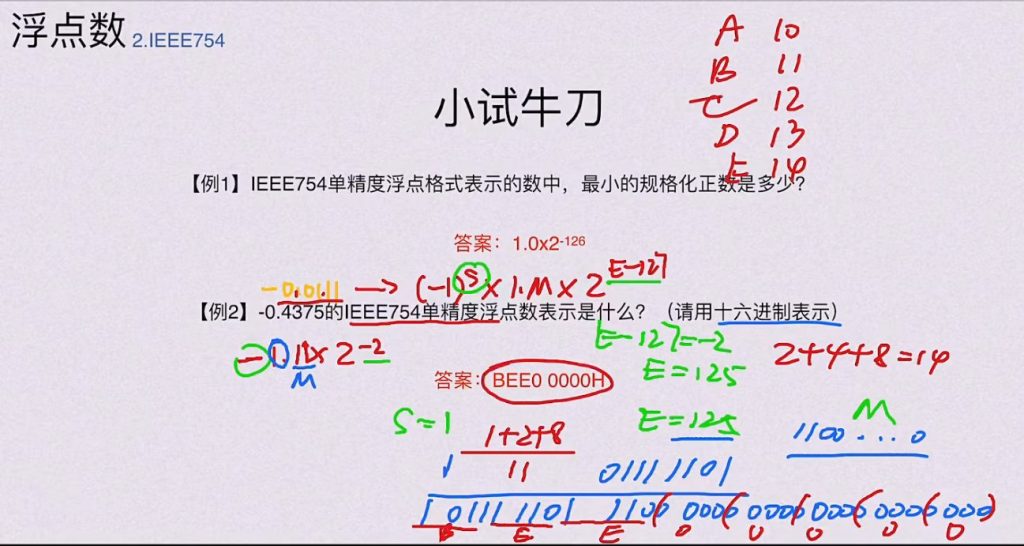
5.2.5 小试牛刀

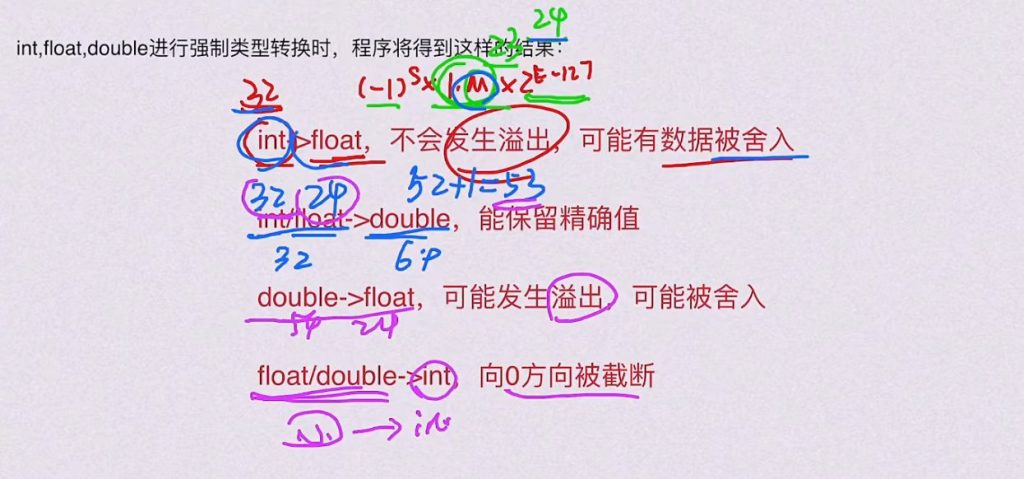
5.3 C语言中浮点数类型
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


