第二章 01数制与编码

数据如何在计算机中表示？

运算器如何实现数据的算术和逻辑运算

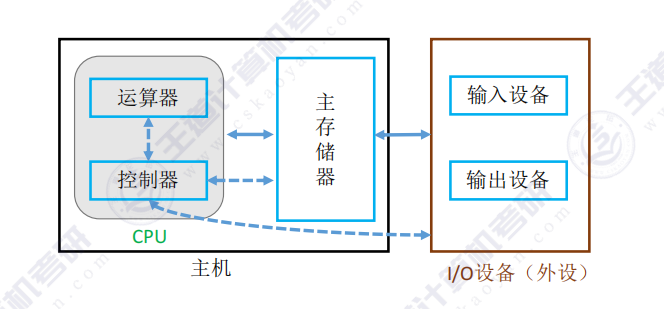
一、进位计数制

1.1 知识总览

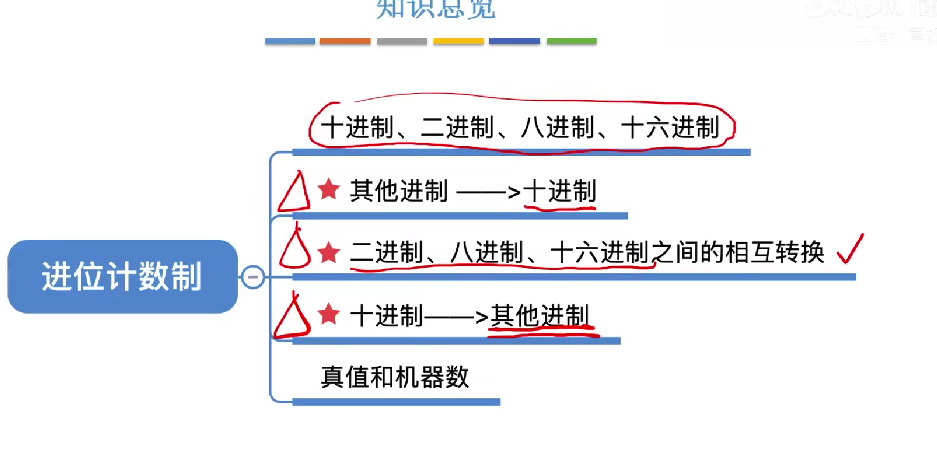
1.2 最古老的计数方法

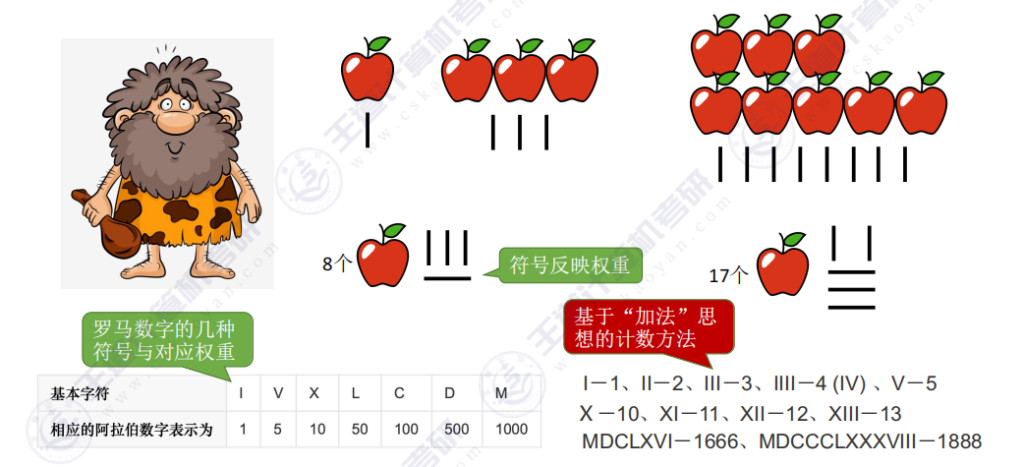
• 符号权重表示法：使用不同符号表示不同数量，如竖线（权重1）和横线（权重5），8个苹果用1横3竖表示，17个用3横2竖表示。
• 罗马数字系统：
  • 基本符号对应关系：I(1), V(5), X(10), L(50), C(100), D(500), M(1000)
  • 组合示例：II=2, III=3, IV=4, V=5, XI=11, MDCLXVI=1666, MDCCCLXXXVIII=1888
• 加法思想：数值计算通过符号权重相加实现，如MDCLXVI=1000+500+100+50+10+5+1
• 局限性：大数表示需要不断发明新符号（如用W表示10000），随着数字增大变得不便

1.3 十进制计数法

位置权重：符号、位置决定其权重

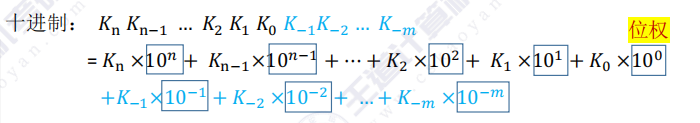
1.4 推广：r进制计数法辅助进制：八进制和十六进制因与二进制转换简便（1位十六进制=4位二进制）而常用

二进制加法

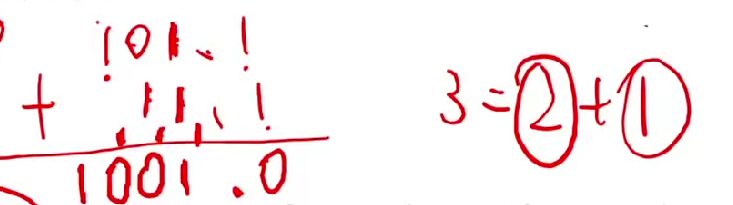
八进制加法

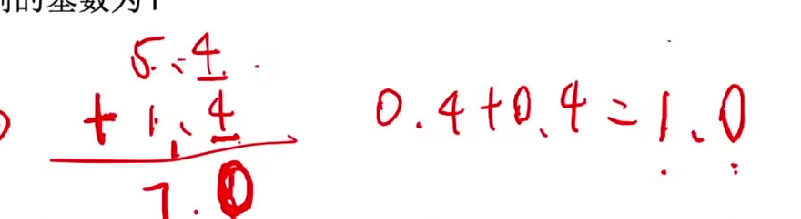
十六进制加法

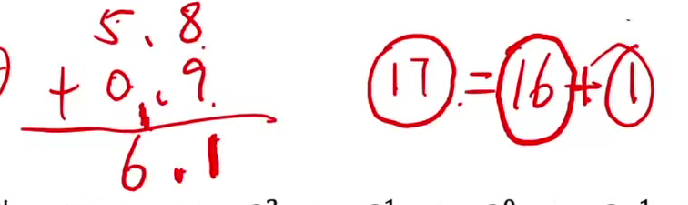
辅助进制：八进制和十六进制因与二进制转换简便（1位十六进制=4位二进制）而常用

1.5 任意进制→十进制

1.6 二进制→八进制、十六进制

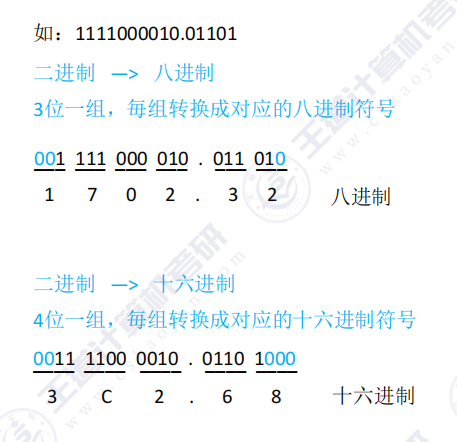
• 二进制转八进制
  • 补位规则:
    • 整数部分不足3位时左侧补零
    • 小数部分不足3位时右侧补零

• 二进制转十六进制
  • 分组原则: 4位二进制对应1位十六进制

1.7 八进制、十六进制 -> 二进制

1.8 各种进制的书写方式

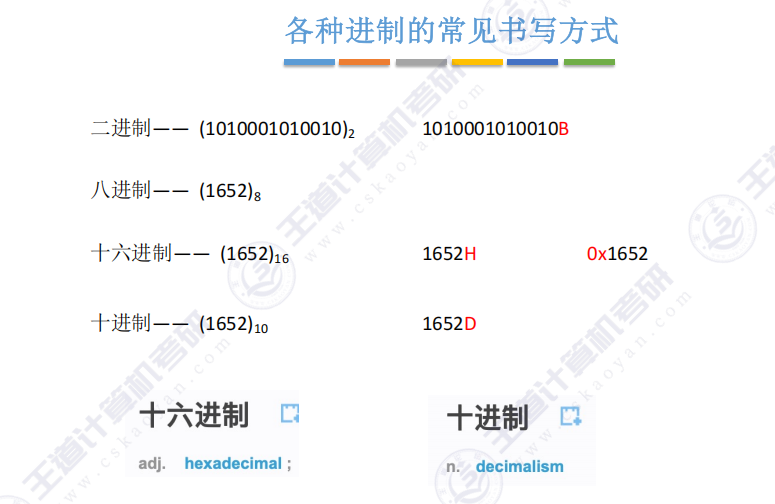
进制	基数	表示前缀 / 后缀	允许字符	示例
十进制	10	无	0~9	128、2048
八进制	8	0	0~7	0377（对应十进制 255）
二进制	2	0b/0B，后缀B	0、1	0b11111111（对应 255）
十六进制	16	0x/0X、后缀H	0~9、A~F（a~f）	0x3FF（对应 1023）

1.9 十进制->任意进制

（1）整数部分处理

（2）小数部分处理

基本原理：通过反复乘以基数r，取整数部分作为对应数位的值

操作步骤：

• 用小数部分乘以r，记录整数部分（最高小数位K_−1​）
• 用新小数部分继续乘以r，取整数作为下一位K₋₂
• 重复直到小数部分为0或达到所需精度

部分十进制小数无法精确表示为二进制（如0.3），会出现无限循环

1.10 十进制->二进制（拼凑法）

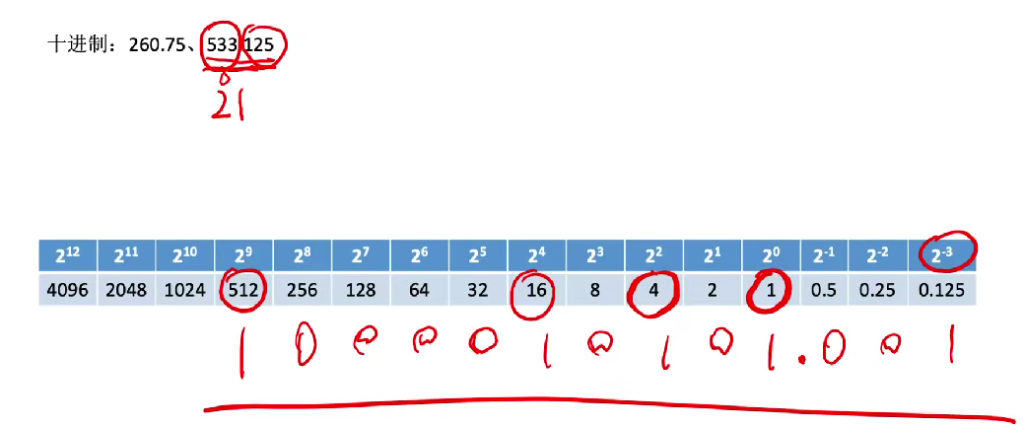
• 可先转二进制再转其他进制（如八进制）

1.11 真值和机器数

• 概念区分:
  • 真值：符合人类习惯的实际数值（带正负号的数值）
  • 机器数：计算机中存储的数字形式（将正负号数字化为0或1）
• 表示方法：通过增加符号位（0表示正，1表示负）解决十进制数带正负的问题
• 后续内容：将学习原码、反码、补码等计算机表示带符号数的方法

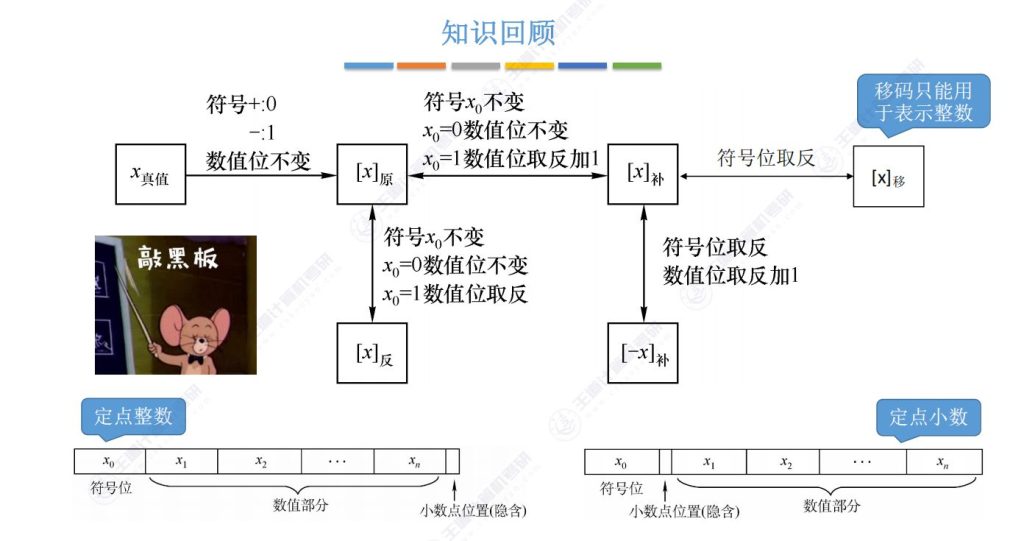
1.12 知识回顾

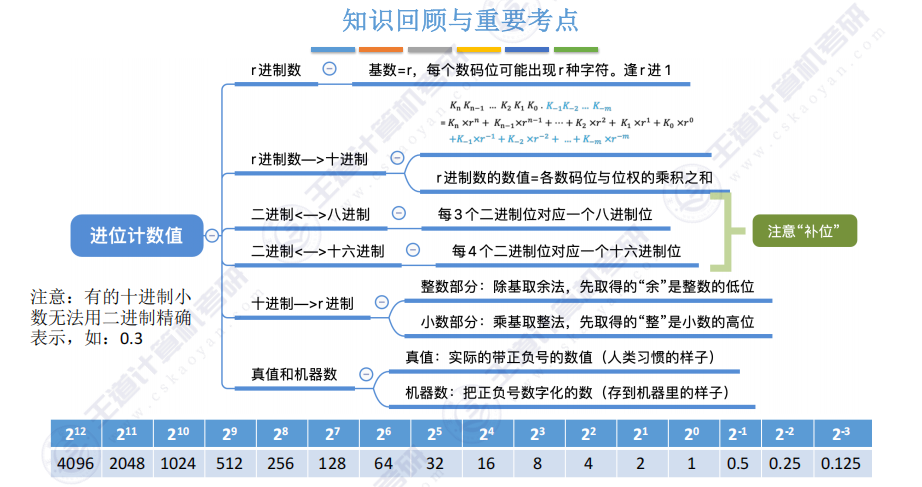
二、定点数的编码表示（重点）

2.1 知识总览

2.2 定点数和浮点数

• 定义区别：
  • 定点数：小数点位置固定不变，类似十进制常规计数方式（如123.45）
  • 浮点数：小数点位置浮动，类似科学计数法，需配合阶码表示

2.3 无符号数的表示

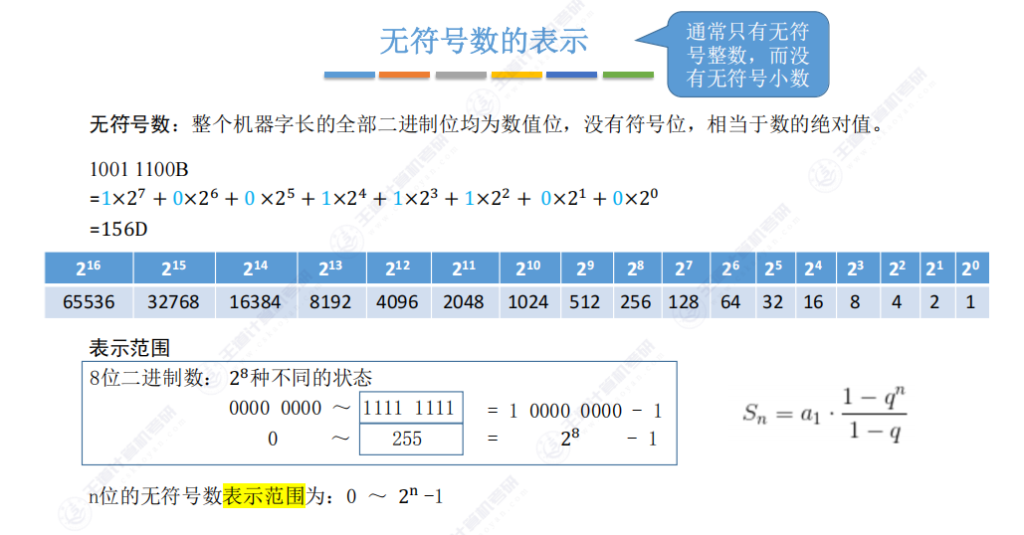
• 通常只有无符号整数，而没有无符号小数

• unsigned int / long(unsigned float 报错)

2.4 有符号数的表示

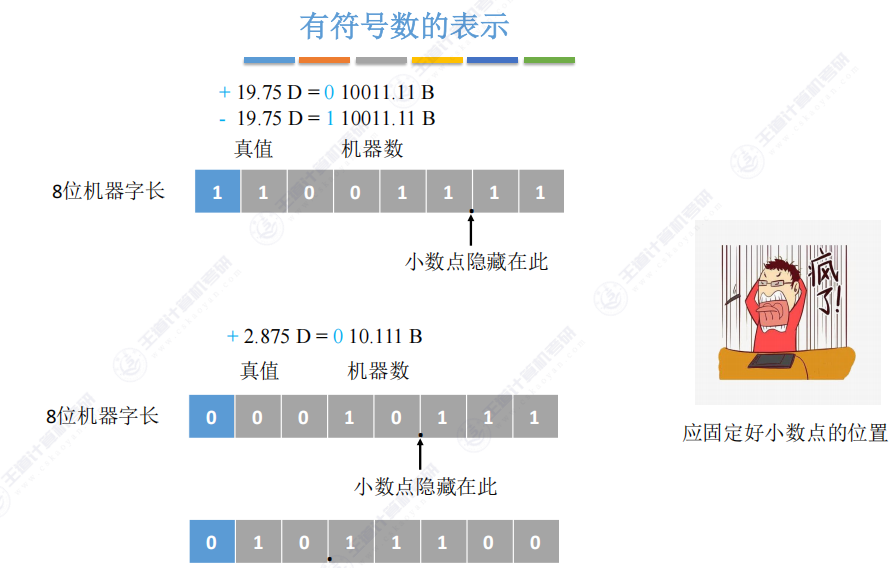
2.5 有符号数的定点表示

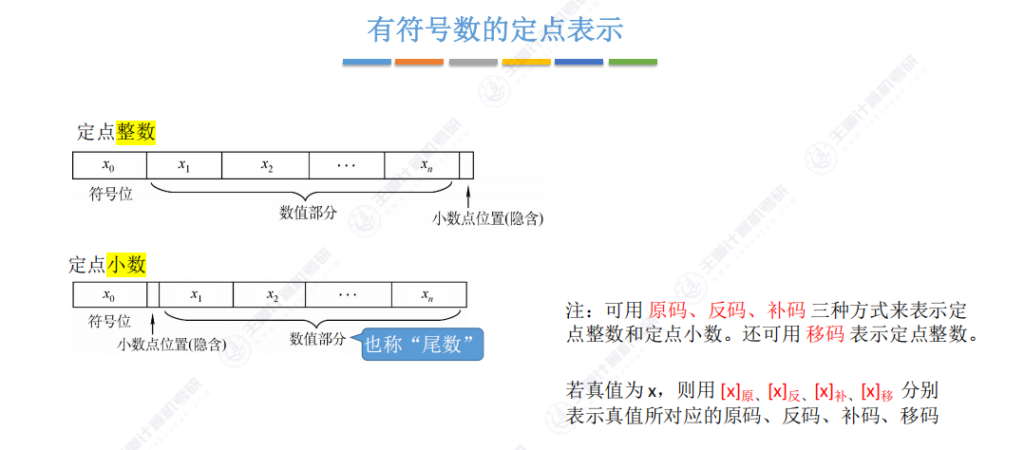
• • 定点整数：
    • 小数点隐含在最低位后
    • 最高位为符号位（0正1负）
    • 示例：+19D原码=0,0010011；-19D原码=1,0010011
  • 定点小数：
    • 小数点隐含在符号位后
    • 最高位为符号位（0正1负）
    • 示例：+0.75D原码=0.1100000；-0.75D原码=1.1100000
  • 尾数：表示数值部分的二进制位
  • 符号位：最高位表示正负

2.6 原码

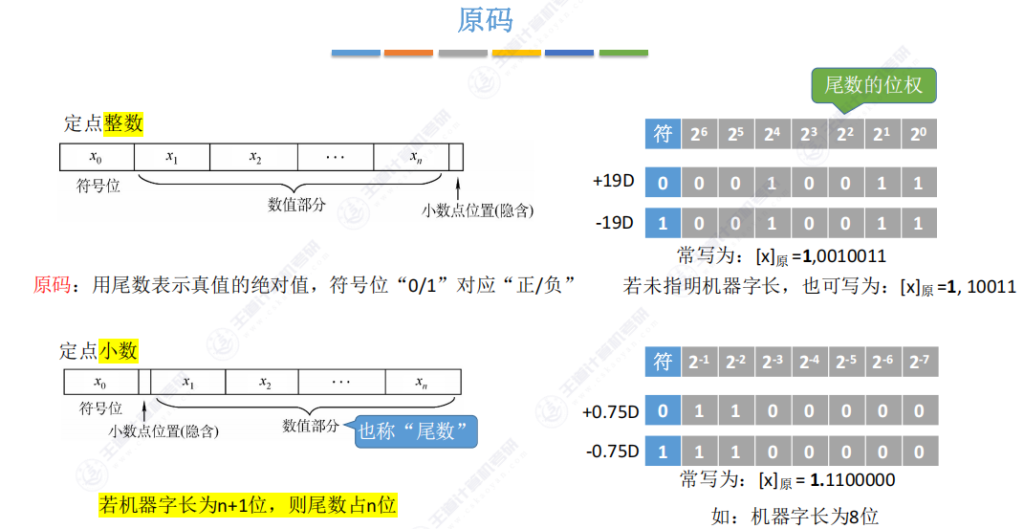
• 原码
  • 定义：用尾数表示真值的绝对值，符号位单独表示
  • 定点整数示例：
    • +19D：符号位0，尾数=16+2+1=0010011 → [x]原=0,0010011
    • -19D：符号位1，尾数不变 → [x]原=1,0010011
  • 定点小数示例：
    • +0.75D：0.5+0.25 → 尾数1100000 → [x]原=0.1100000
    • -0.75D：符号位取反 → [x]原=1.1100000
  • 书写规范：
    • 符号位后可用逗号/点分隔（如1.1100000或1,1100000）
    • 不足位需补零（根据机器字长）

原码范围表示

2.6 反码

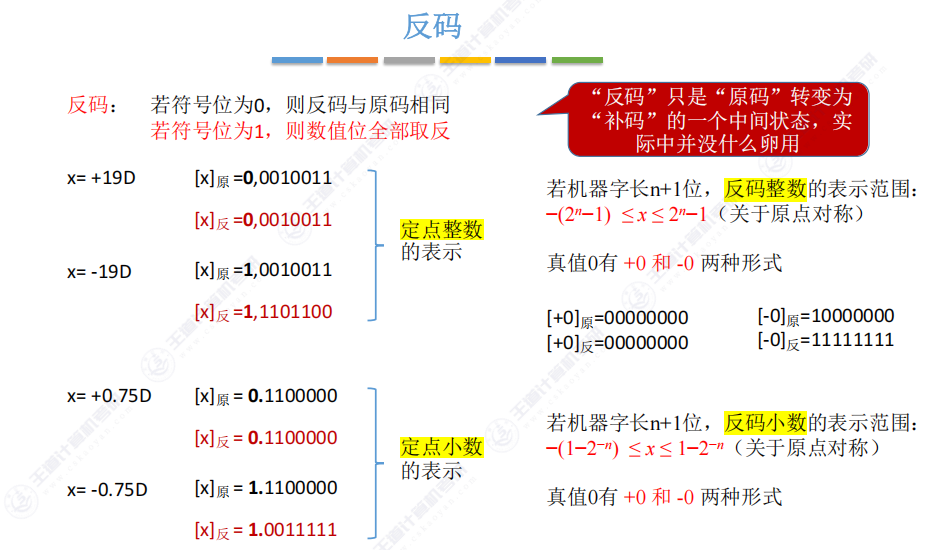
2.7 补码

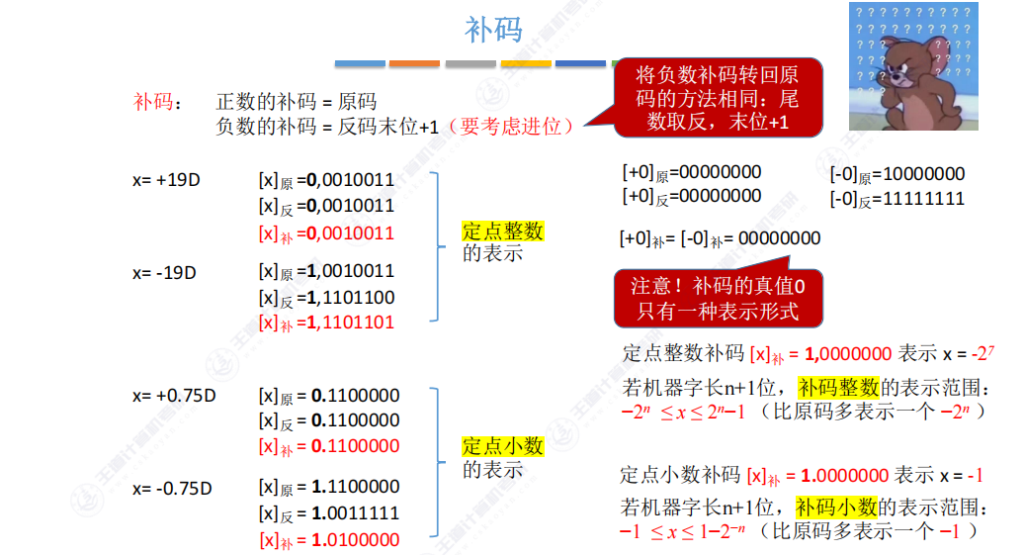
将负数补码转回原码的方法相同:尾数取反，末位+1

2.8 移码 – 表示的整数很方便对比大小

补码的基础上将符号位取反得到移码

移码只能用于表示整数

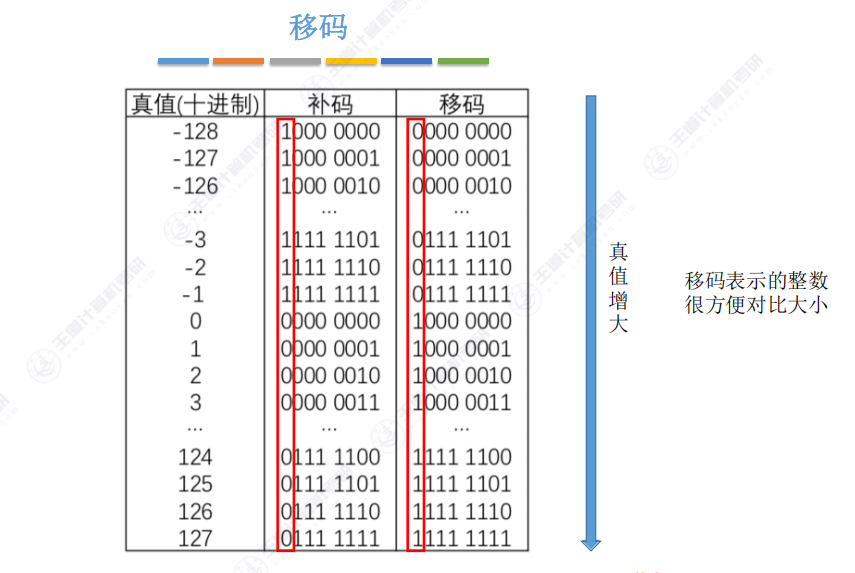
• 移码
  • 定义：在补码基础上将符号位取反
  • 特点：
    • 只能表示整数，不能表示小数
    • 零的表示只有一种形式（与补码一致）
    • 表示范围与补码相同
  • 优势：
    • 真值增大时，移码对应的无符号数也逐一递增
    • 便于计算机硬件比较大小（从高位到低位依次比较）

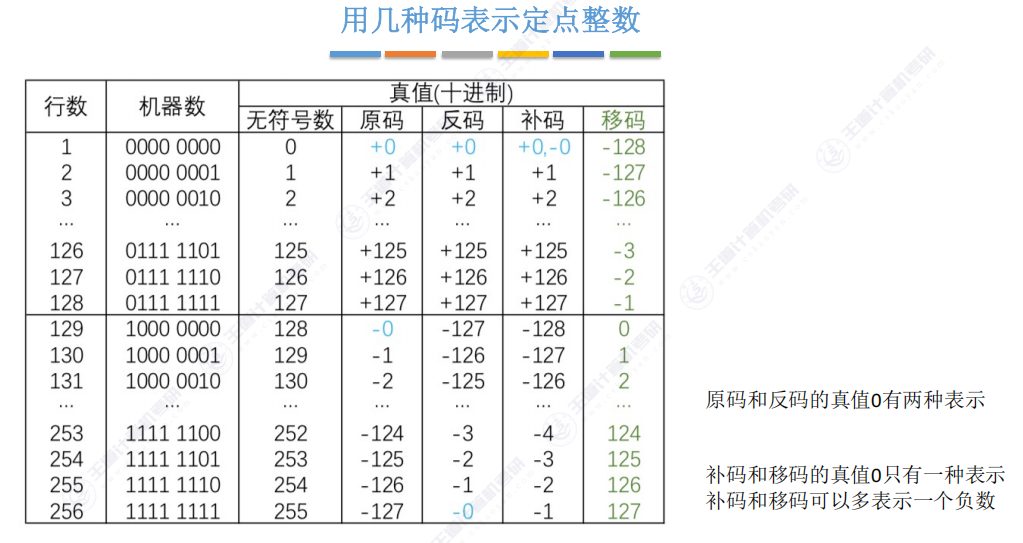
2.9 用几种码表示定点整数

2.10 练习

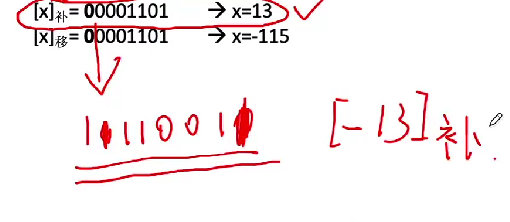
2.11 知识总结

三、各种码的作用

3.1 加减运算

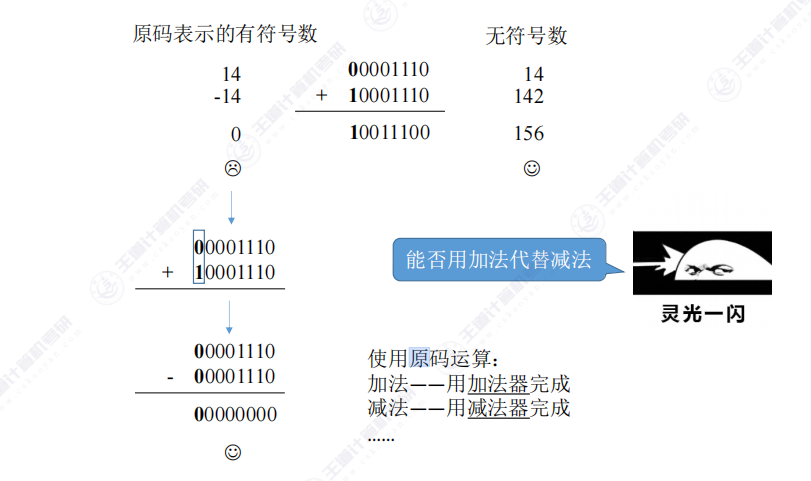
原码表示缺陷：当对原码进行加减运算时，若正数加负数（如14+(-14)），直接相加会得到错误结果（10011100），必须转换为正数减正数（14-14）才能得到正确结果0
硬件实现问题：原码运算需要同时设计加法器和减法器电路，其中减法器设计更复杂，会增加硬件成本和复杂度

3.2 用加法代替减法

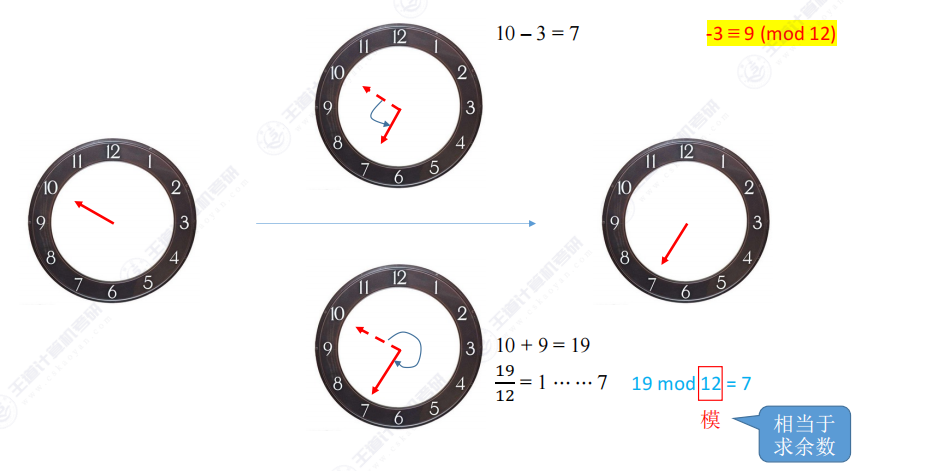
3.3 模运算的性质 – 求补码

模运算等价性：在模12条件下，-3和9等价（互为补数）

在(mod m)的条件下，若能找到负数的补数，就可以用正数的加法来等价替代减法

两个数互为补数需满足：①模运算下等价；②绝对值之和等于模

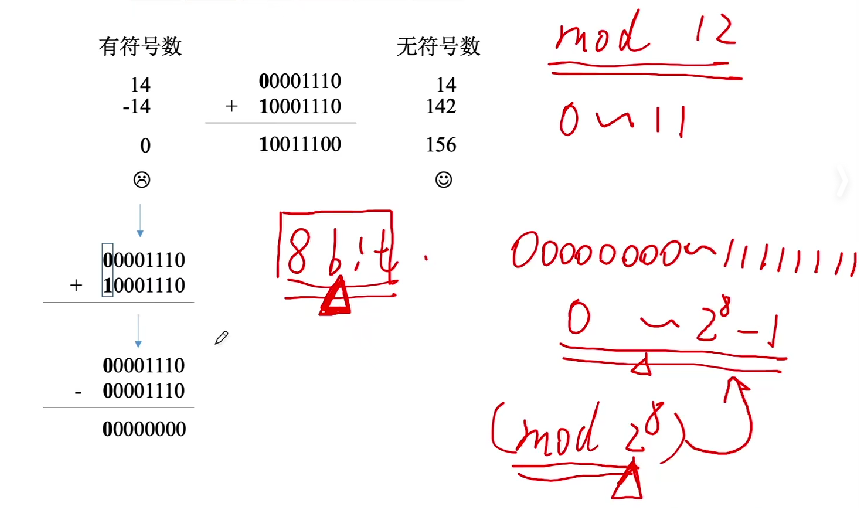
求补码

公式：模-a的绝对值=a的补数，等价于符号位不变，原码取反+1

3.4 加减法练习

求补码：

1、减数去掉符号，得66，也就是01000010

2、全部取反+1得补码 10111110

四、C语言中的强制类型转换

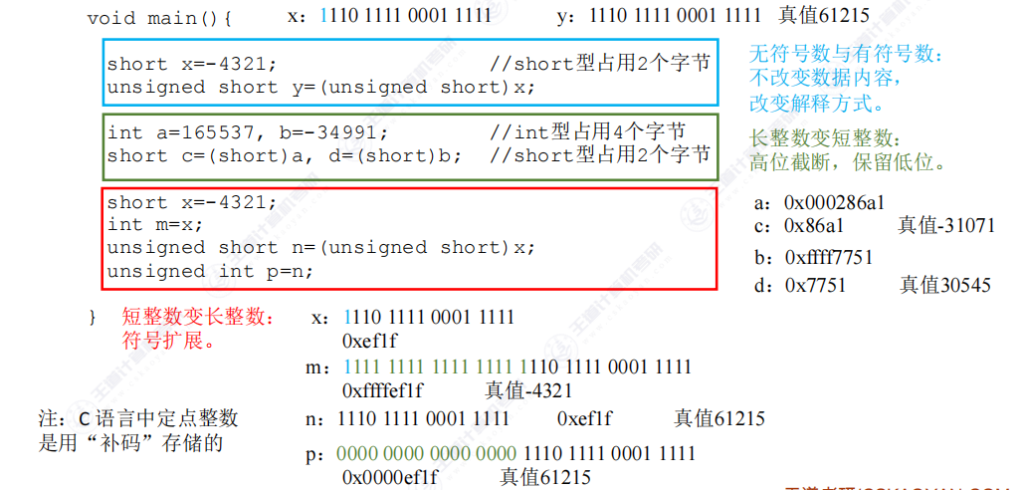
• 存储方式: C语言中所有定点整数(int/short/long)均采用补码形式存储，unsigned修饰的为无符号数
• 转换基本原则: 强制类型转换不改变底层二进制表示，仅改变解释方式

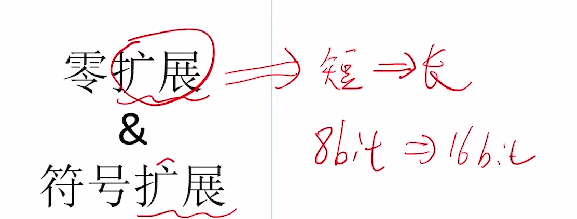
五、零扩展和符号扩展

5.1 为什么需要对数据进行长度扩展

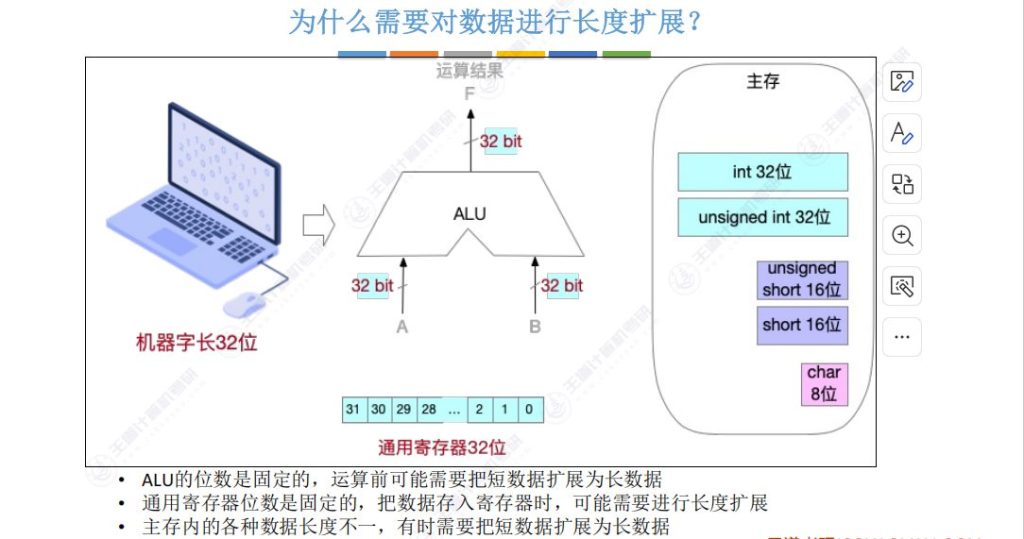
• 硬件需求：计算机的机器字长决定了通用寄存器位数和ALU运算位数（通常固定为32位），而主存中存储的数据长度各异（如int型32位、short型16位、char型8位），运算前需统一扩展至寄存器/ALU位宽
• 软件场景：程序赋值时可能涉及不同长度变量的转换（如short bshort\ bshort b赋值给int aint\ aint a），此时需要进行长度扩展
• 处理流程：数据需先存入通用寄存器再传给ALU运算，这两个环节都可能需要将短数据扩展为长数据（如16位→32位）

5.2 扩展方法 （零扩展、符号扩展）

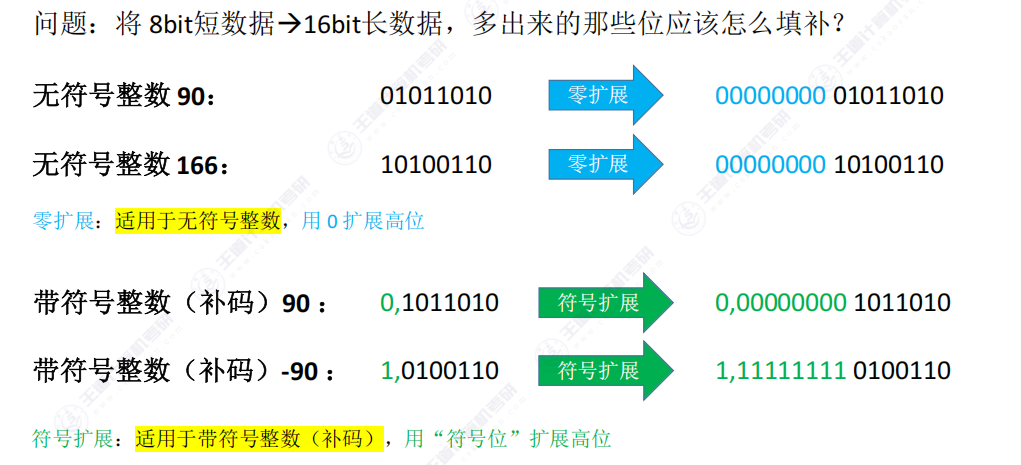
• 零扩展适用于无符号整数，扩展时高位补 0，保持数值不变（如 8 位无符号数 90 扩展为 16 位时，直接在高位补 0）。
• 符号扩展适用于带符号整数的补码表示，高位补符号位（正数补 0，负数补 1），以保持补码真值不变（如 8 位补码 – 90 扩展为 16 位时，高位补 1）。
  核心区别：零扩展不改变无符号数的数值，符号扩展确保有符号数补码的正确性，负数若误用零扩展会导致真值错误。