一、古典概型
1、古典概型:具有以下两个特征的试验称为古典概型
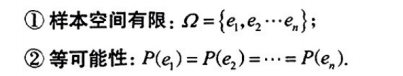
2、计算方法:

3、古典概型的性质

4、古典概型例题1 – 放回和不放回问题

解析
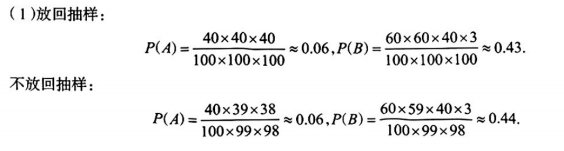
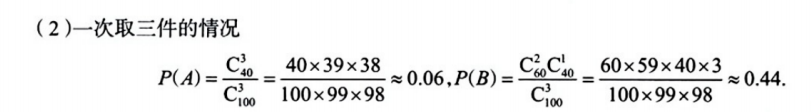
古典概率计算中,往往要用到排列与组合数数,若是一次取一件无论是放回还是不放回抽样,我们都将其当成排列来计算,此时最易犯错误的是漏掉产品间的顺序,从上面这个例子,我们容易看到:一次取一件不放回取三次与一次取三件计算事件的概率时结果一样,这不是巧合,适用于一般情况,以后如果遇到一次取一件不放回取几次计算事件的概率,我们可以将其当成一次取几件,此时我们可用组合计算,这样也可避免漏掉产品间的顺序.
5、古典概型例题2
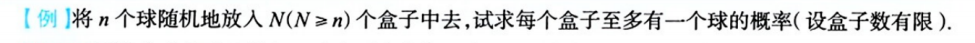
解析


二、几何概型
1、几何概型的定义

2、何时用几何概型
①在某个区间( 区域)内随机取数或者任意取点;
②在某个时间段内随机到达某个地方;
③在某个区间( 区域)内任意子区间(区域)上取值概率与该区间( 区域 )的长度( 面积)成正比.
3、何时用长度比?何时用面积比?
①通过实验条件若只产生一个变量时用长度比,产生两个变量时用面积比.
例如:在一个区间随机取一个数,求该数落在某个区间的概率,用长度比;
在一个区间随机取两个数,求两数之差小于多少的概率,用面积比.
②若条件是在某个区间内任何子区间上取值概率与该区间长度成正比,则用长度比;
若条件为在某个区域内任何子区域上取值概率与该区域面积成正比,用面积比.
4、几何概型例题1

解析
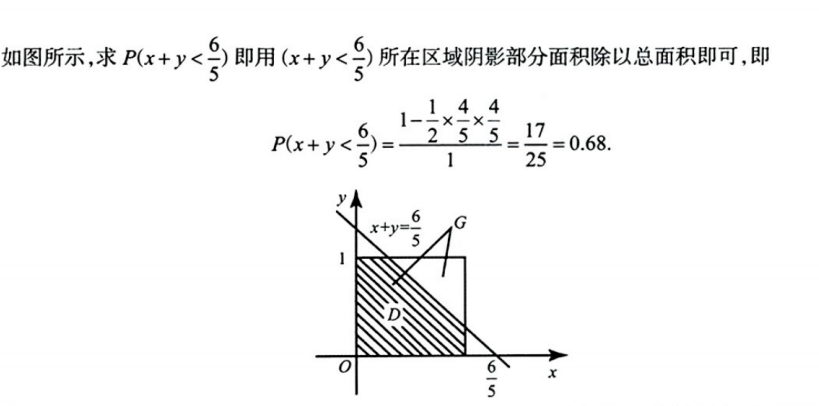
5、几何概型例题2

解析
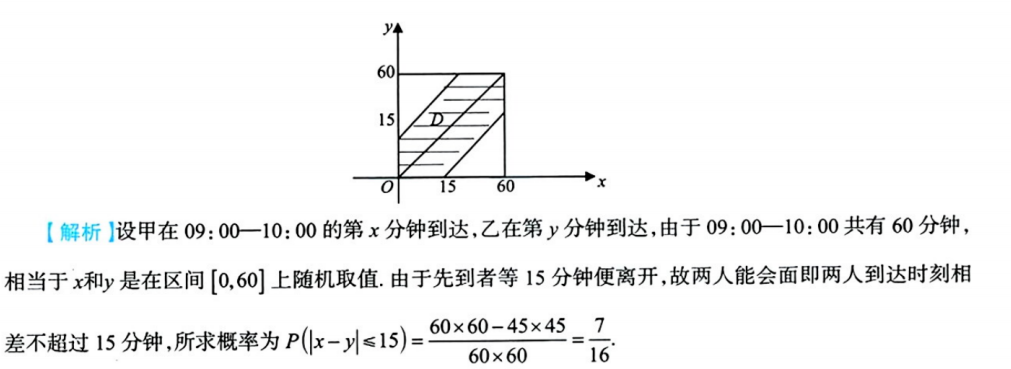
6、几何概型例题3

解析
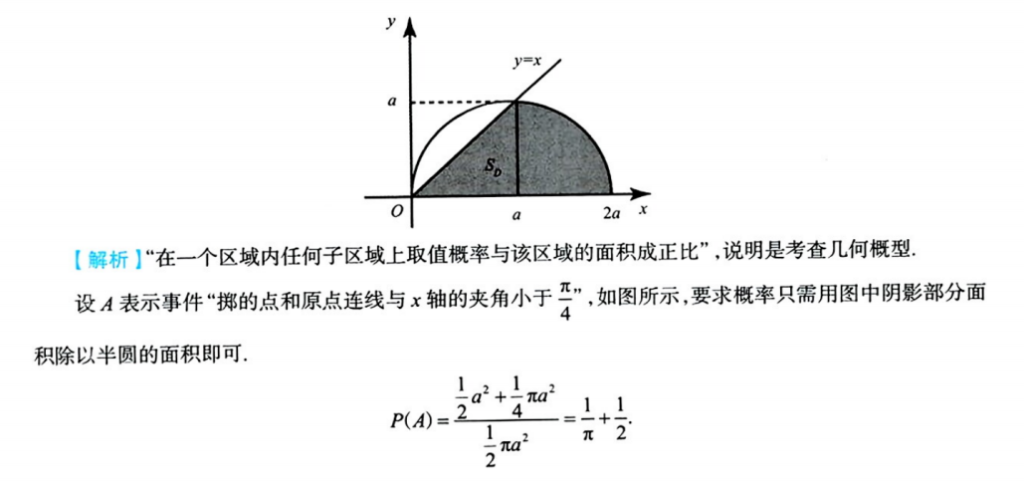
7、几何概型例题4
解析
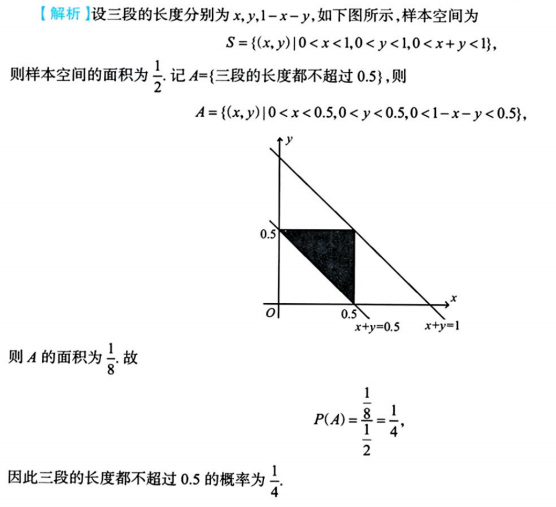
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


