一、重要知识点
1、A、B、C不多于一个发生的 逆事件 至少两个不发生
2、几何概型的应用:只有一个变量用长度比;两个变量用面积比
3、至少一件次品的逆事件表示一件次品都没有
4、古典概型计算问题

5、概率推不出事件

6、抓阄问题和抽签问题,抽出后不放回
第N次取次品的概率与第一次取次品的概率相等
7、概率为0的事件与任何事件都独立
8、多个事件相互独立的结论

二、错题、难题汇总
| 题目 | 备注 |
| 3.1.2 | 抽样问题 |
| 3.4.1\3.4.2\3.4.4 | 几何概型 |
| 3.3.2 | 古典概型问题\N个盒子放n个球问题 |
| 3.5.2 | 概率计算 |
| 3.6.4 | 乘法公式 – 抓阄问题 |
| 3.6.5 | 抽签原理 |
| 3.7.1 | 全概率公式的应用 |
| 3.7.2 | 全概率公式的应用 |
| 3.9.2 | 两两独立问题 |
| 3.9.4 | 独立问题 |
| 3.9.5 | 概率为0的事件与任何事件都独立 |
三、李良课本习题
3.1 排列、组合
3.1.1


3.1.2



3.2 随机事件关系
3.2.1


3.3 古典概型
3.3.1

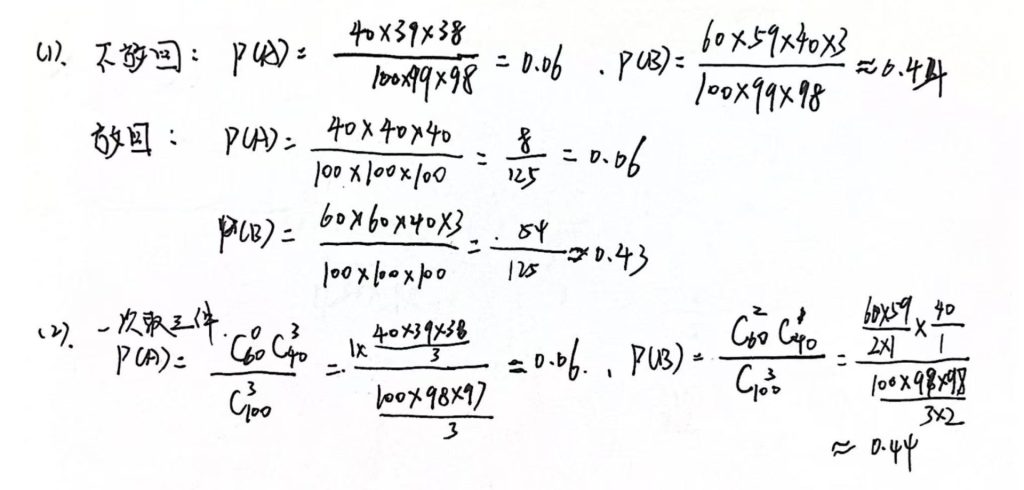

3.3.2
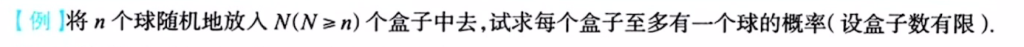

问题设定
- 有n个球(通常假设球是不同的)
- 有N个盒子(通常假设盒子是不同的)
- 每个球都要放入某个盒子
- 求:每个盒子至多有一个球的概率
分析思路
1. 总的放球方法数 每个球都可以放入N个盒子中的任意一个,所以总的放球方法数为:N^n
2. 满足条件的方法数 “每个盒子至多有一个球”意味着所有球都在不同的盒子里(即没有两个球在同一个盒子)。
这要求:n ≤ N(球数不能超过盒子数)
满足条件的方法数是:
- 第1个球有N种选择
- 第2个球有(N-1)种选择(不能选第1个球已选的盒子)
- 第3个球有(N-2)种选择
- …
- 第n个球有(N-n+1)种选择
所以满足条件的方法数为:N × (N-1) × (N-2) × … × (N-n+1) = N!/(N-n)!
3. 概率计算 P = 满足条件的方法数 / 总方法数 = [N!/(N-n)!] / N^n
具体例子
例1:3个球,5个盒子
- 总方法数:5³ = 125
- 满足条件的方法数:5 × 4 × 3 = 60
- 概率:60/125 = 12/25 = 0.48
例2:4个球,4个盒子
- 总方法数:4⁴ = 256
- 满足条件的方法数:4! = 24
- 概率:24/256 = 3/32 ≈ 0.094
直观理解
- 当n = N时:这相当于把n个不同的球放入n个不同的盒子,每个盒子恰好一个球,这是排列问题
- 当n < N时:相当于从N个盒子中选n个来放球,然后安排这n个球的顺序
- 当n > N时:至少有一个盒子必须放多个球,所以概率为0
实际应用 这个模型在现实中有很多应用:
- 生日问题:n个人,365天,求没有人同一天生日的概率
- 哈希冲突:n个数据,N个哈希槽,求无冲突的概率
- 停车问题:n辆车,N个车位,求每个车位至多停一辆车的概率
概率变化规律
- 当n固定时,N越大,概率越大(盒子多,重复可能性小)
- 当N固定时,n越大,概率越小(球多,重复可能性大)
3.4 几何概型
3.4.1

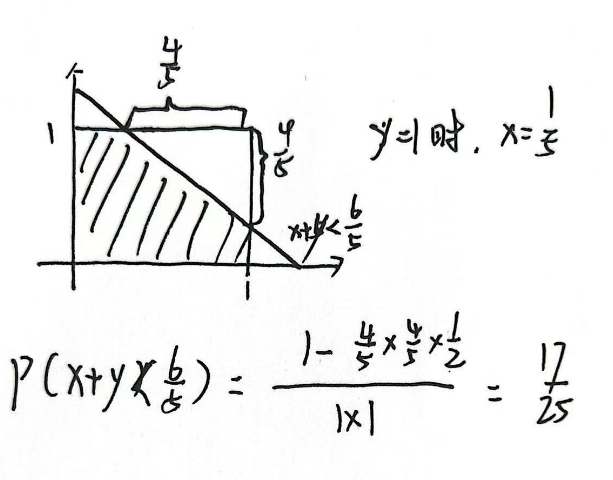
3.4.2

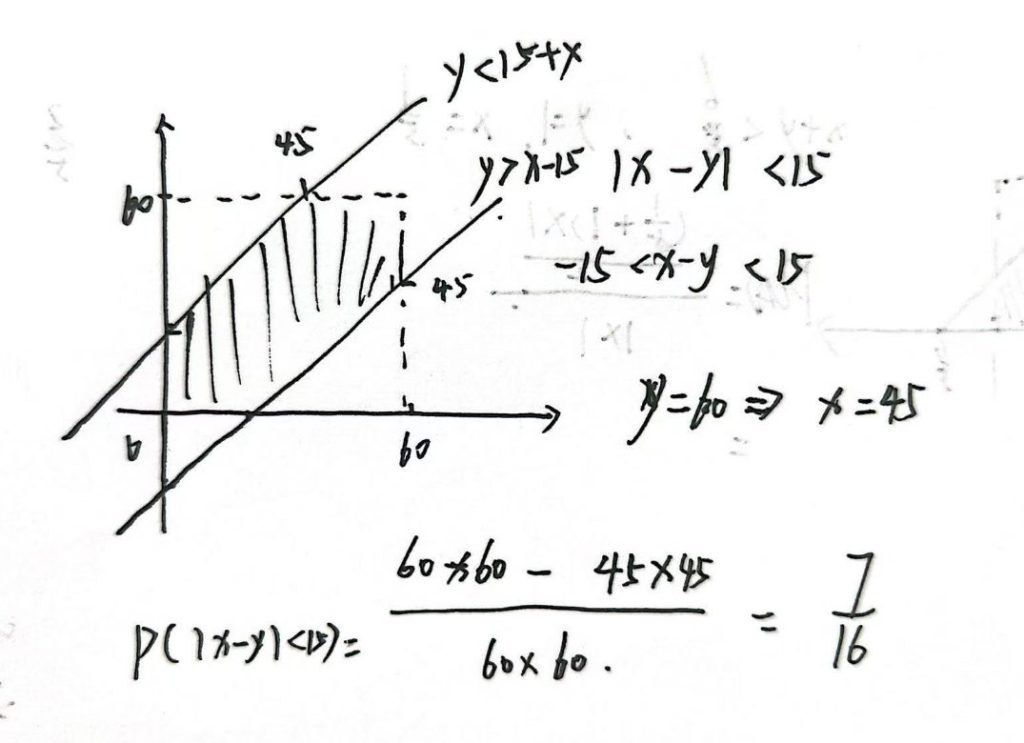
3.4.3

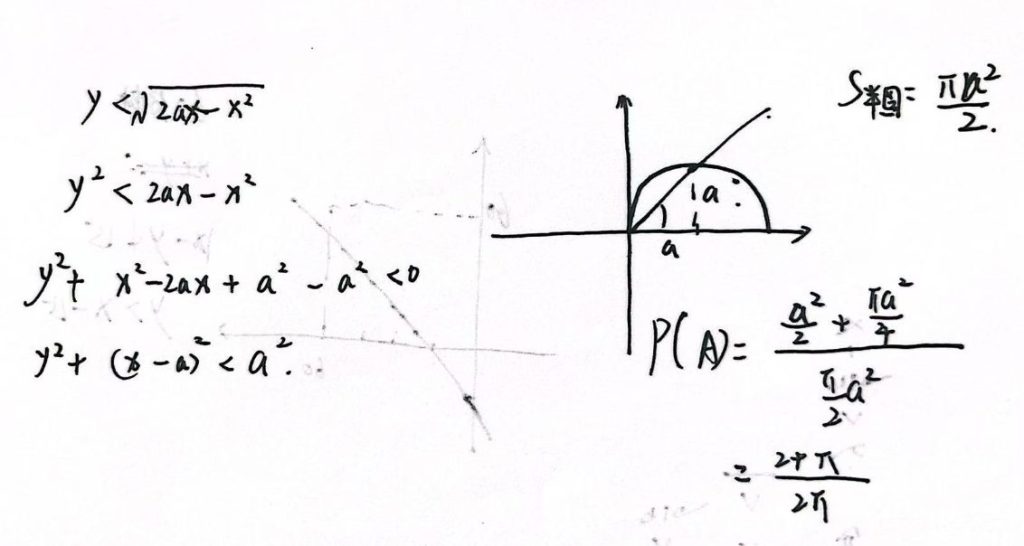
3.4.4

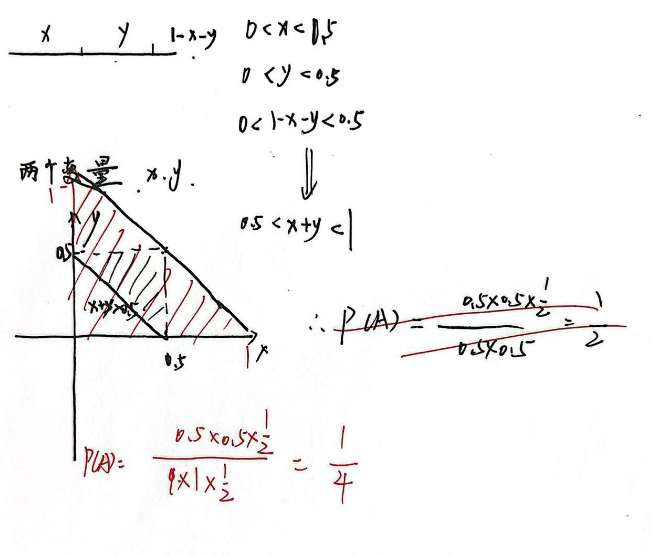
3.5 概率的公理化定义和性质
3.5.1

C- 概率推不出事件

3.5.2


3.5.3
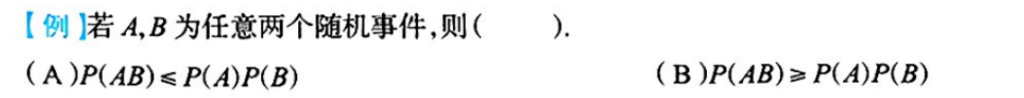

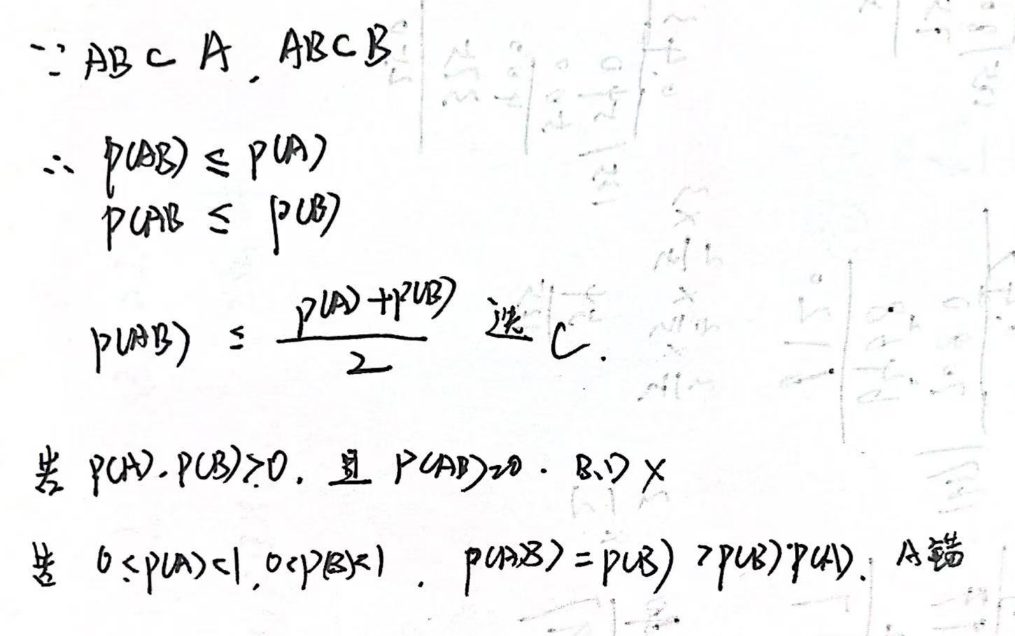
3.5.4
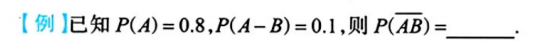
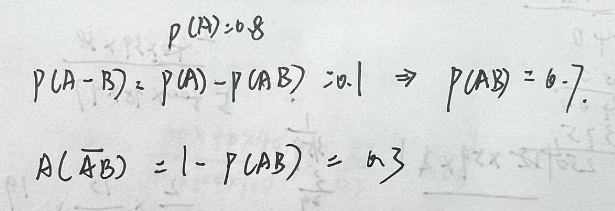
3.5.5
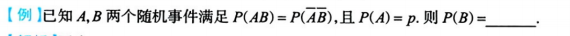
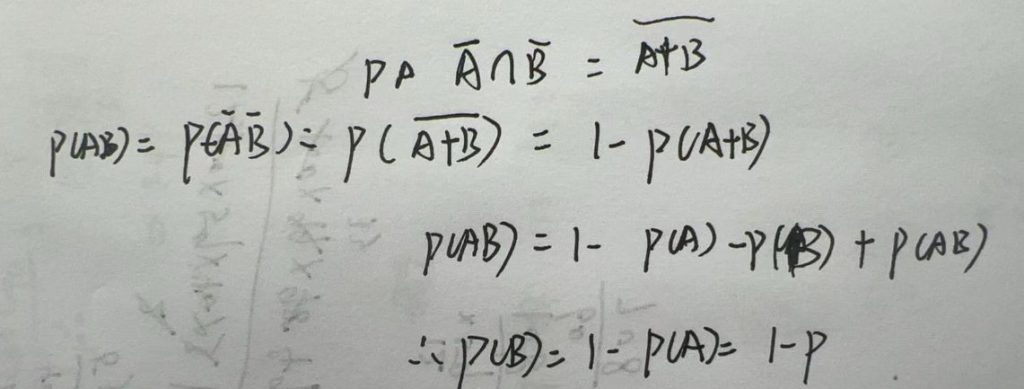
3.5.6
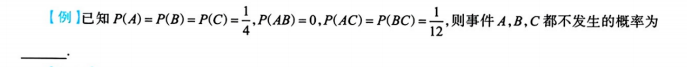

3.5.7

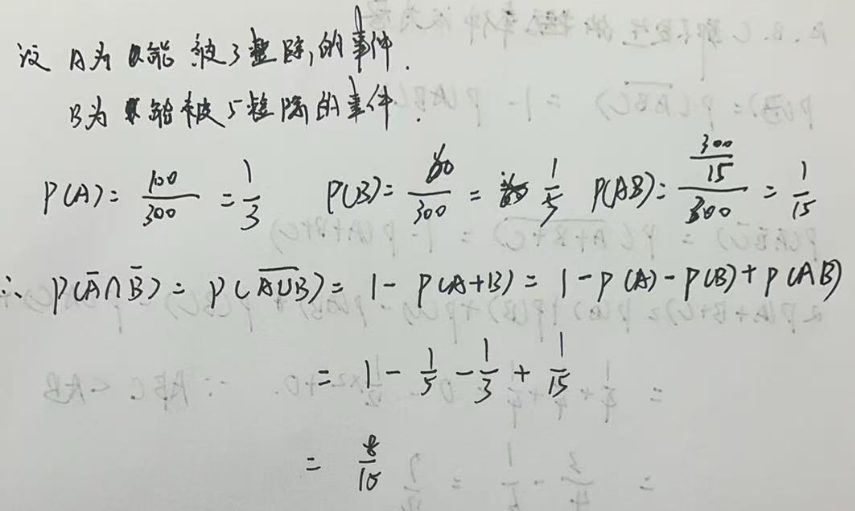
3.6 条件概率及其性质
3.6.1
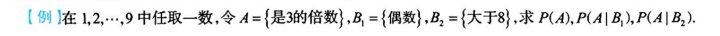
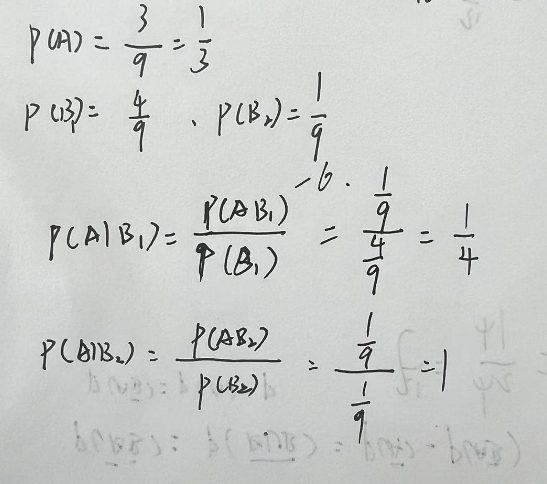
3.6.2
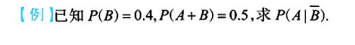
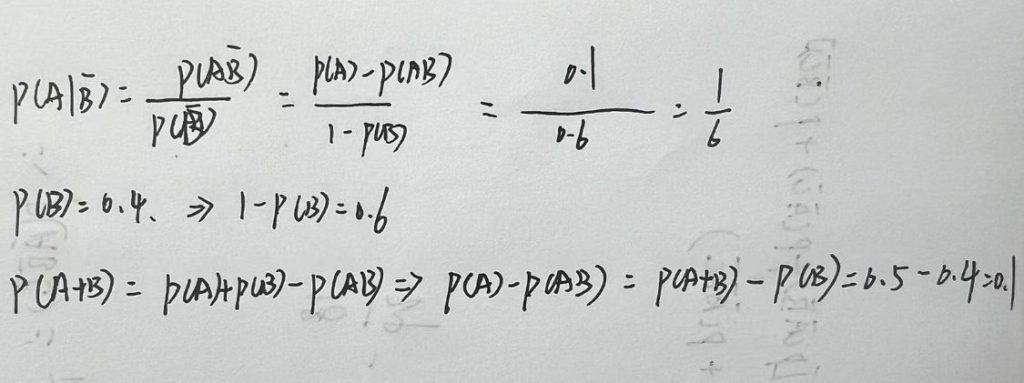
3.6.3
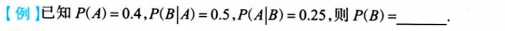
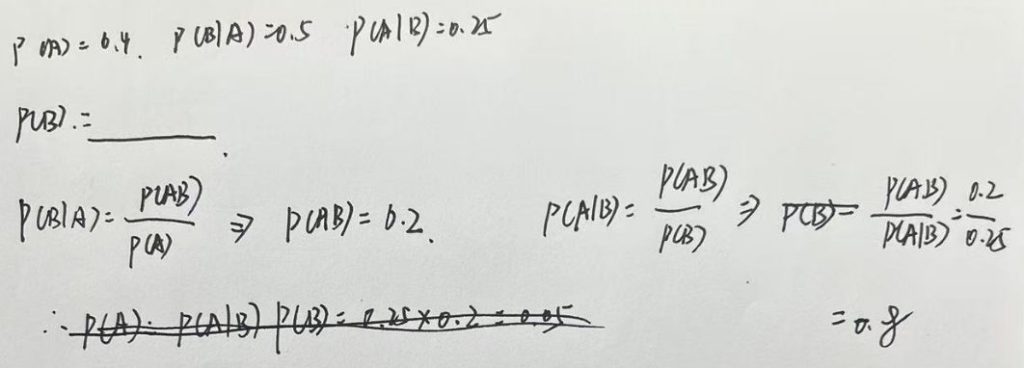
3.6.4 抓阄问题


3.6.5 抽签原理


3.7 全概率公式
3.7.1
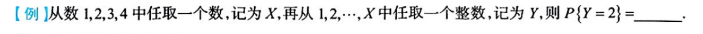

3.7.2



3.8 贝叶斯公式
3.8.1



3.8.2



3.9 独立事件
3.9.1

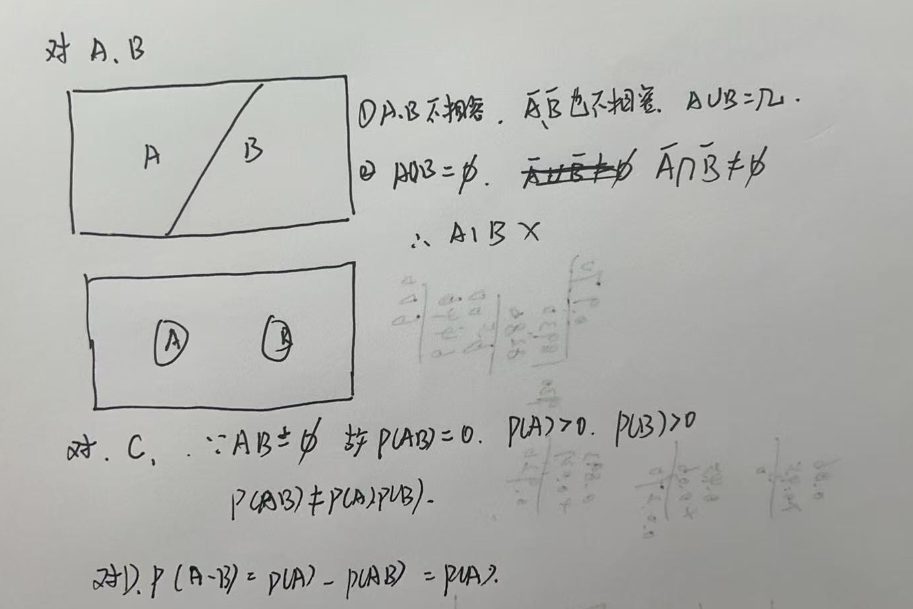

3.9.2
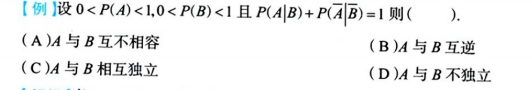
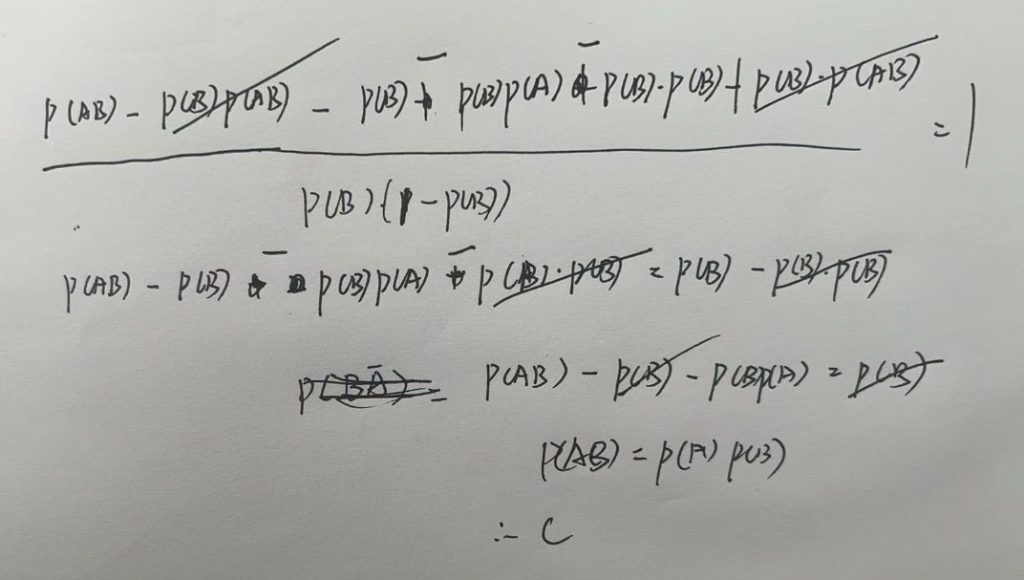

3.9.3 三个事件独立


3.9.4


3.9.5

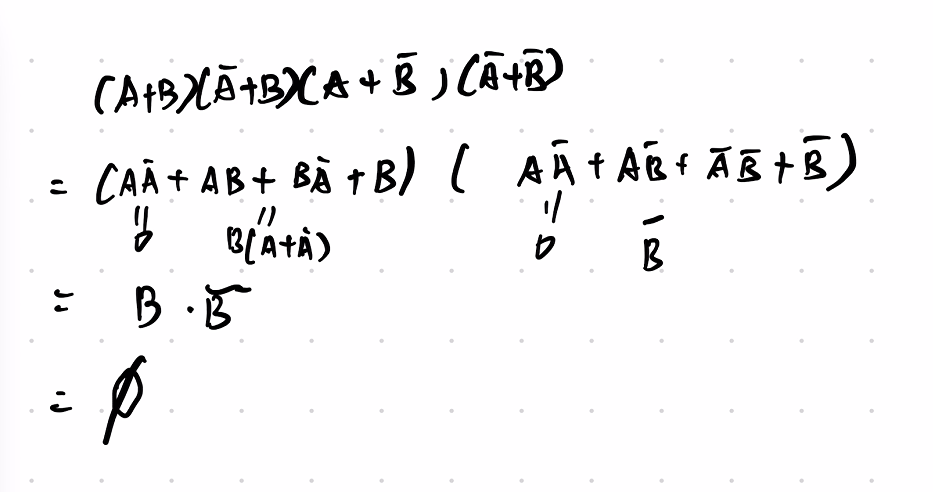
3.9.6


3.9.7

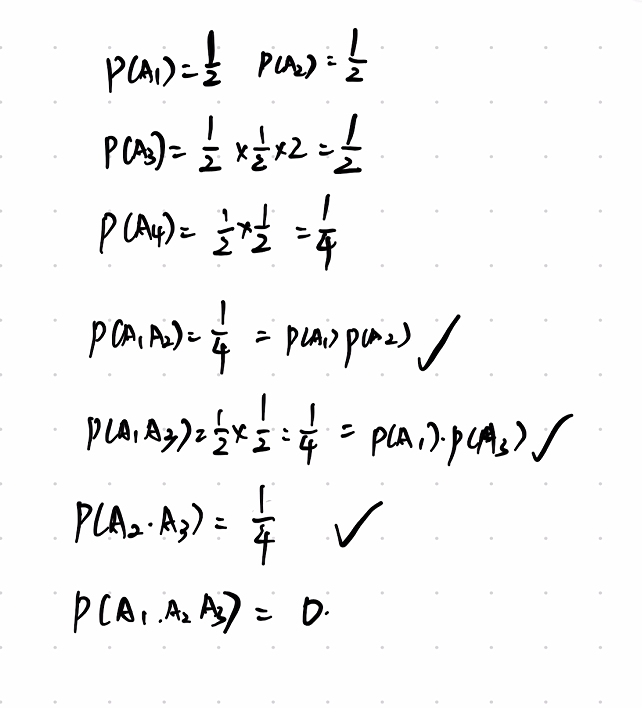
3.10 n重伯努利试验
3.10.1


3.10.2


3.10.3


本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


