一、基础知识结构
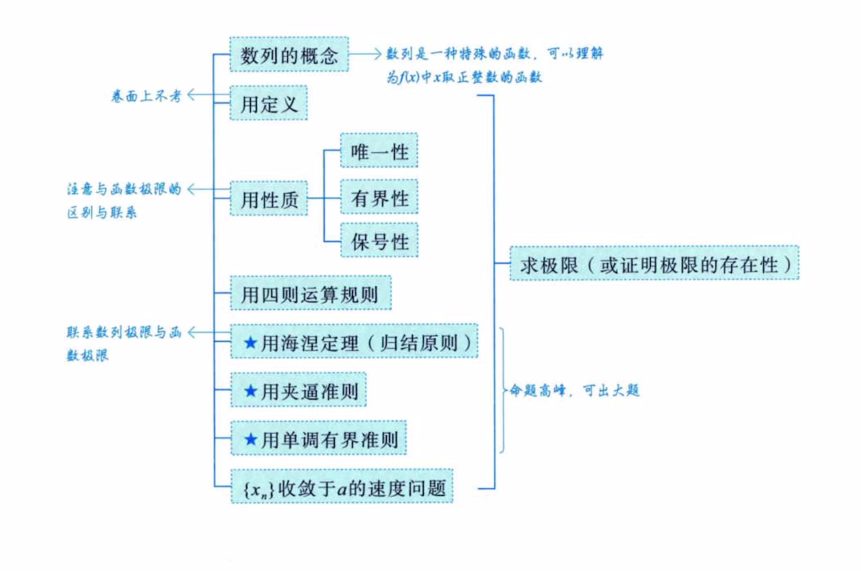
二、重要知识点
1、无穷大量和无界
- 数列 {Xn}是无穷大量,定义是:任意M>0,存在N>0,当n>N时,使Xn的绝对值>M;
- 数列 {Xn}无界,定义是:任意M>0,存在n>0,使Xn的绝对值>M。
- 通俗的语言解释上述两个定义就是: 无穷大量是数列从某项(N)起,其后面的所有项都充分大(不管你M取多大,Xn总比你大,即∞);
- 无界是数列存在某项充分大(即某项∞)。 关键在于无穷大是从某项起之后所有都充分大,而无界是存在某项充分大。



2、等价无穷小

3、夹逼准则结论
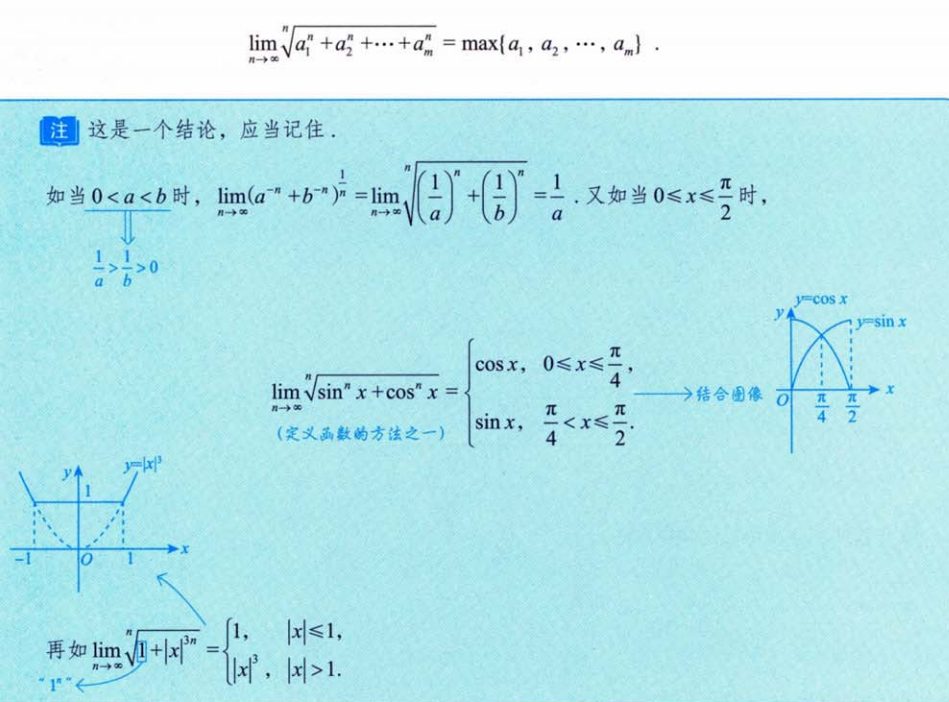
4、关于 x = 2In(1+x)的两种情形
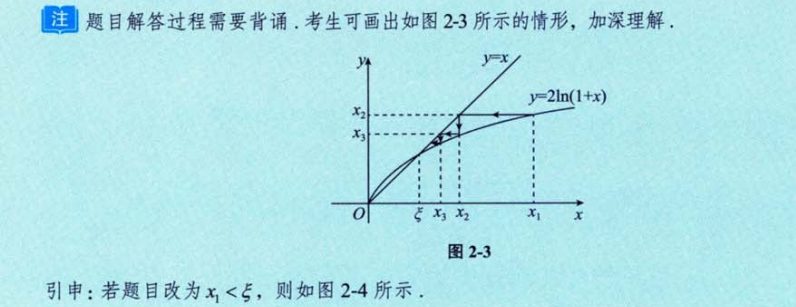
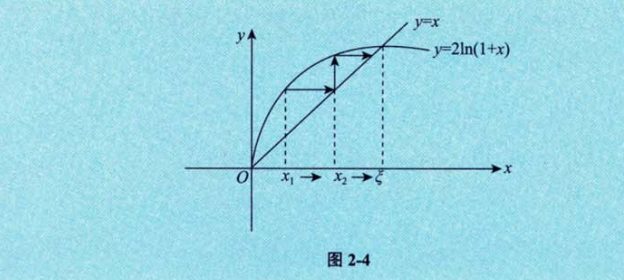
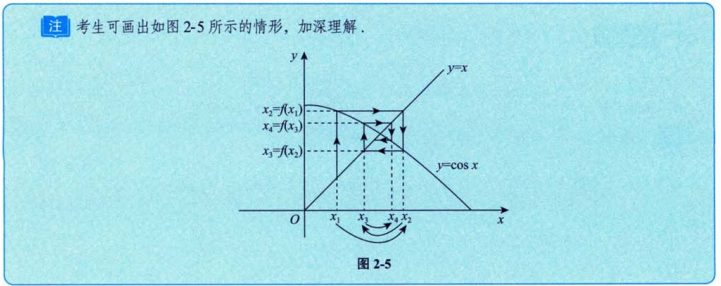
5、数列极限定义问题

e 是不能与 n 有关的
三、错题汇总
| 题号 | 备注 |
| 例题2.5 | |
| 例题2.7 | 海涅原理,注意处理无穷大量和无界量,可以通过取值的方式 |
| 例题2.12 | 单调有限准则 |
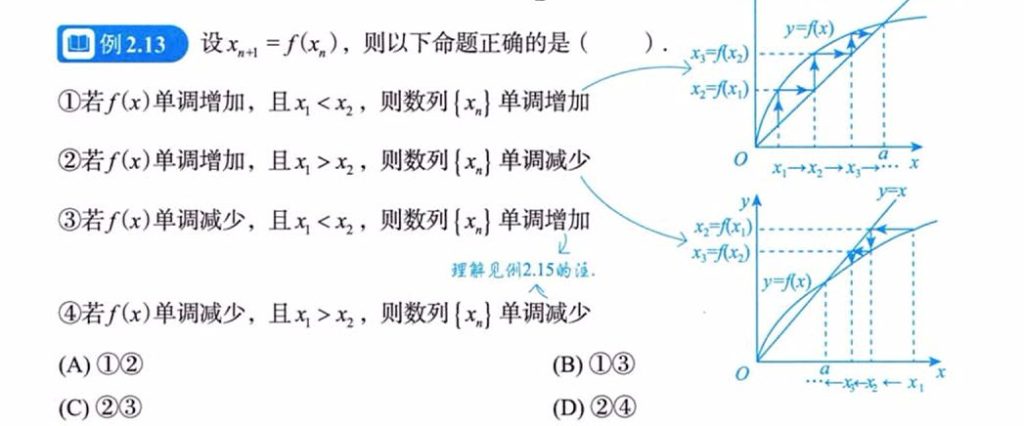
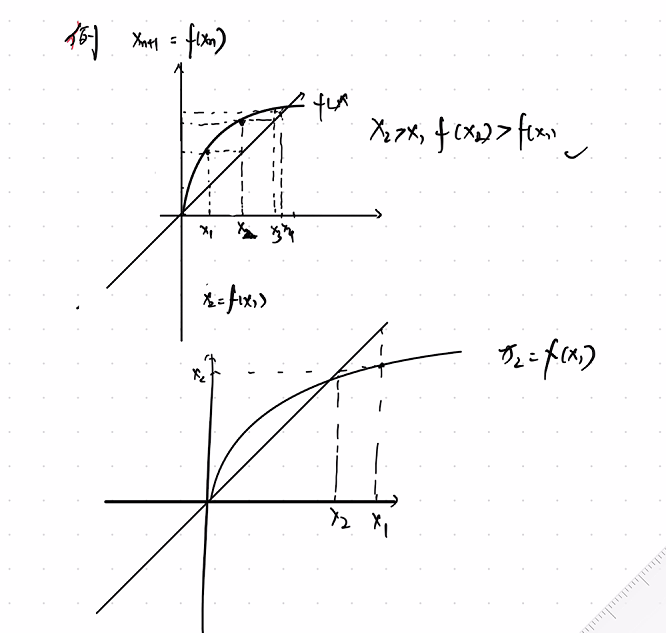
| 例题2.13 | 重点的数形结合 |
| 例题2.14 | 需要背 |
| 例题2.15 | 同2.14,都是单调性求极限问题,需要理解记忆 |
| 例题2.16 | 极限定义概念题,重点 |
| 例题2.17 | 极限定义概念题,重点 |
| 例题2.18 | 极限定义概念题,重点 |
四、题目类型
数列的定义
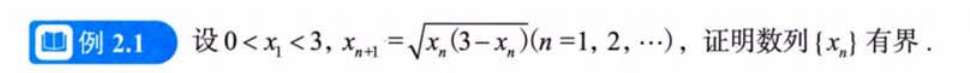

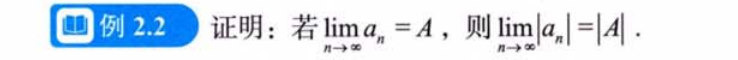









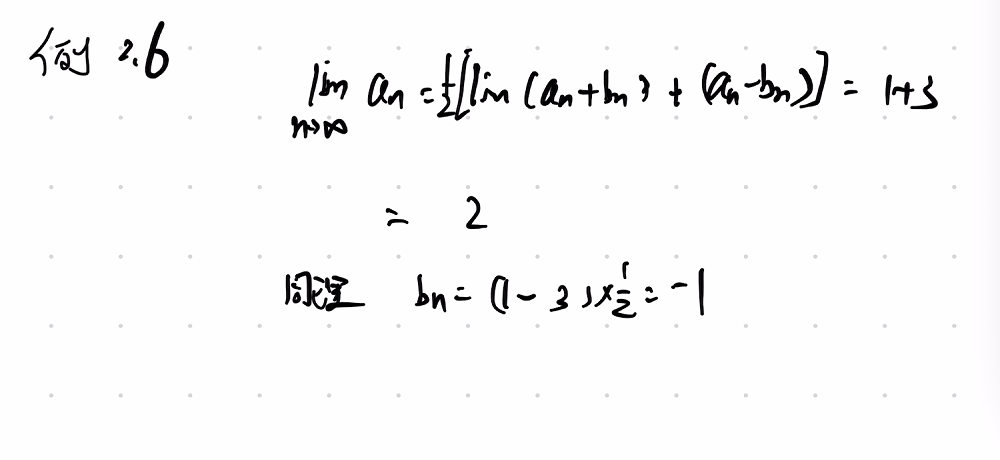




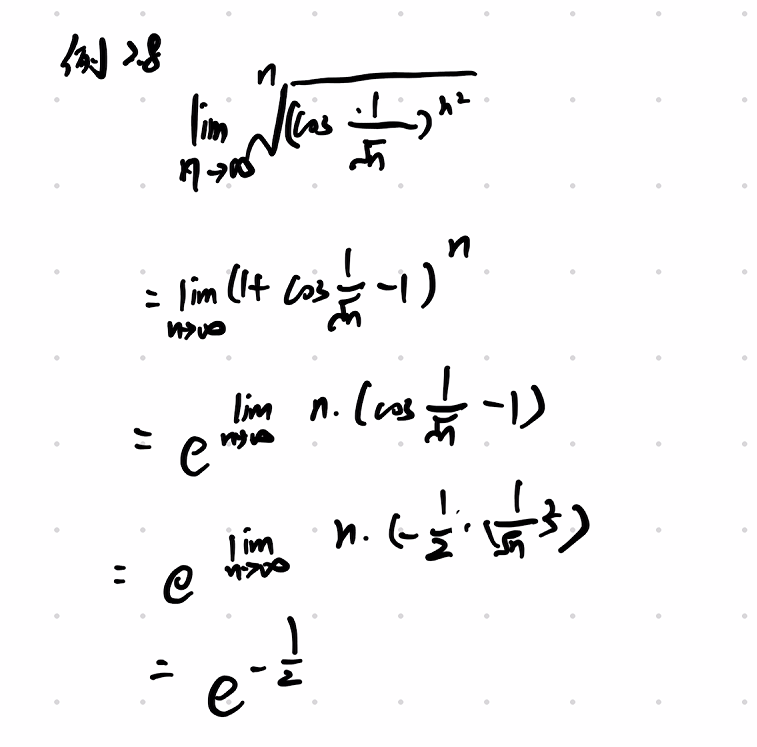
压缩映射原理


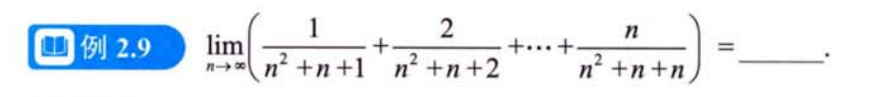

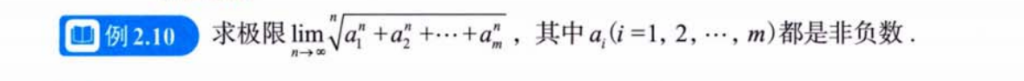




单调有界准则


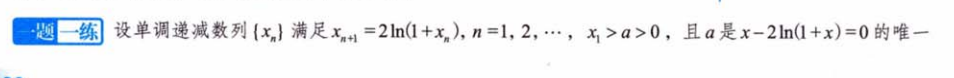
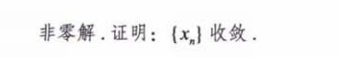

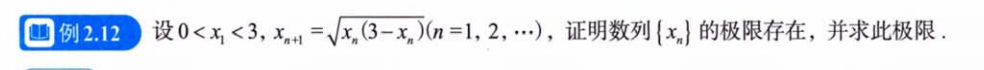





{xn}收敛于α的速度问题








本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客



