微分方程概念及求解
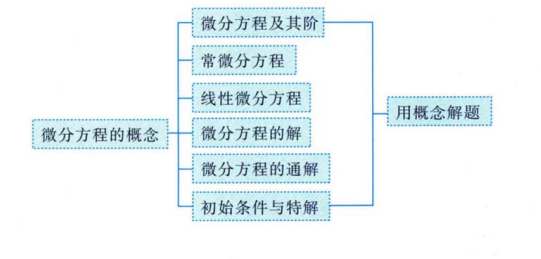
一、微分方程的概念
1、微分方程及其阶
微分方程:是指含有未知函数的导数(或微分)的方程。
- 研究对象是y,求y=y(x)
微分方程的阶:微分方程的 阶数 是指方程中出现的 未知函数的最高阶导数的阶数
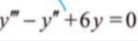
2、常微分方程
未知函数是 一元函数,方程中只包含未知函数的 常导数
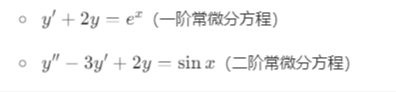
3、线性微分方程
方程中关于未知函数及其导数的项都是 “线性” 的(一次、不相乘)
- n阶线性微分方程
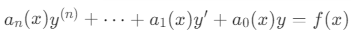
- n阶常系数线性微分方程

4、微分方程的解
4.1定义:
微分方程的解是满足该方程的 函数(包括显式函数、隐式函数或参数方程形式),其核心是将函数代入方程后,方程左右两边恒等。
微分方程解的图形称为积分曲线
4.2解的分类

1、通解的常数 C 并非任意常数,指在一定范围内任意取值的常数,并非实数范围内任意取值;2、C1、C2相互独立指的是相除不等于常数;3、C为了合并,任意写成 InC 形式

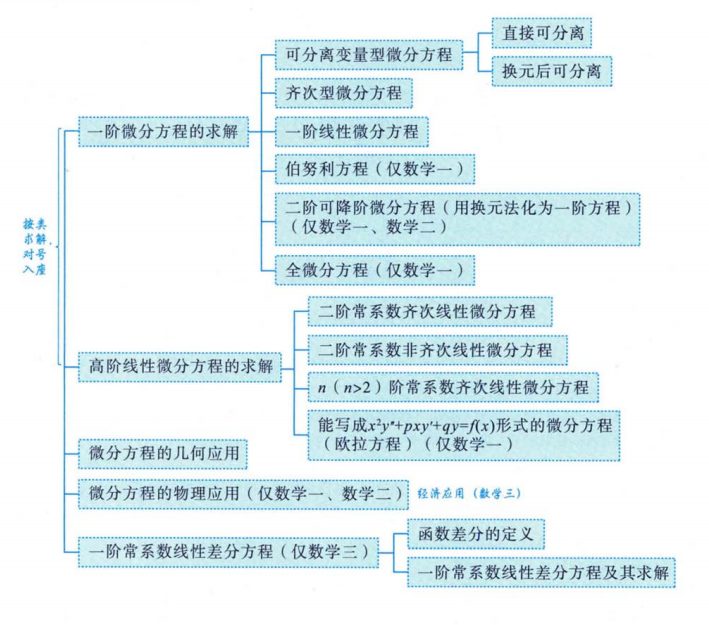
二、一阶微分方程的求解
1、可分离变量型微分方程
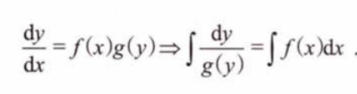
1.1 直接可分离
1.2换元可分离

2、齐次型微分方程

3、一阶线性微分方程

3.1公式推导

3.2注意事项


4、伯努利方程(仅数学一)

5、二阶可降微分方程(数一、数二)
5.1不显含y的,或者不含y和x(思想是把有关y的函数导数去掉)



5.2不显含x


6、全微分方程

三、高阶线性微分方程的求解
1、二阶常系数齐次线性微分方程
1.1 概念

1.2解的结构

1.3通解形式



2、二阶常系数非齐次线性微分方程
2.1概念

2.2解的结构(性质)

2.3特解的设定
待定系数法-求特解:
形式一:

补充说明:
1、一看;二算;三比较;
2、多项式的写法:
比如P = 2 则Q = a;写成一般式
P = 2x + 3 , Q = ax + b
e^ax 直接照抄
形式二:
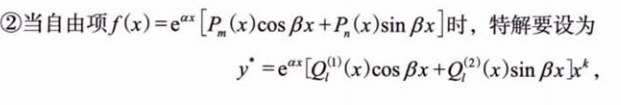


这里的 l 说明:
比如2cosx + xsinx ,按2和x的最高次写一般式,也就是写成ax+b的形式
微分算子法-求特解:
概念

形式一:
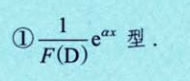
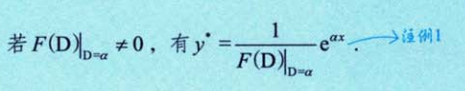
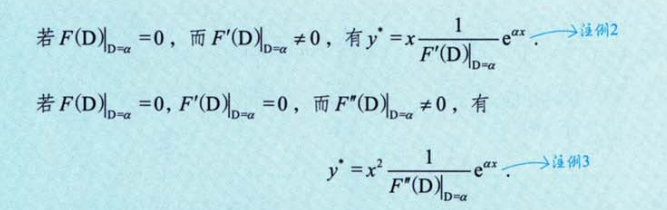
形式一的例子

D=0,求一次导多一个x
形式二
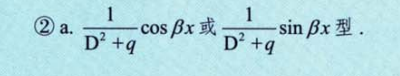
该形式中没有y,只有y”和y
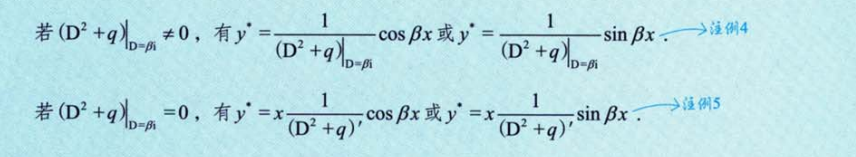
形式二例题
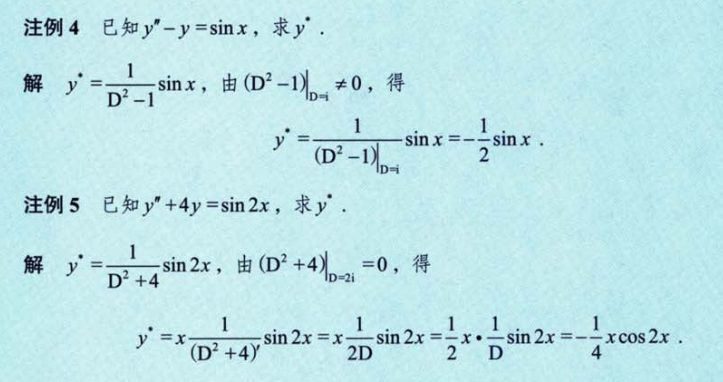
形式三


形式三例题
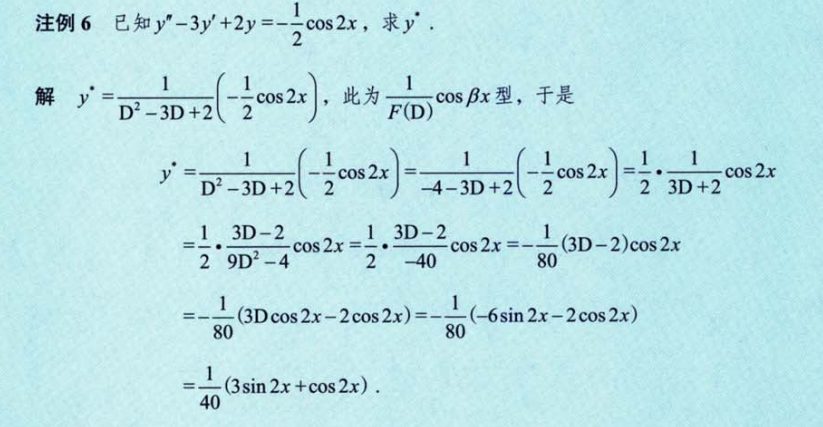
这里只带入D^2
i^2是-1
形式四

形式四例题


形式五
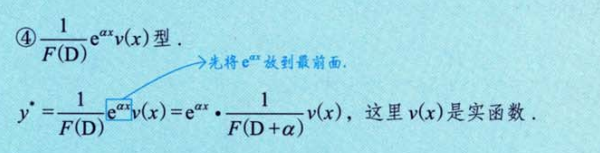
形式五例题

2.4通解

3、n(n>2)阶常系数齐次线性微分方程

四、欧拉方程
1、微分方程的形式
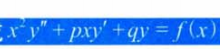

2、欧拉方程的推导

这里需要特别注意x>0还是x<0
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


