2.1 线性表的定义和基本操作
2.1.1 线性表的定义
- 线性表是具有相同数据类型的n(n>0)个数据元素的有限序列。 (其中n为表长,当n=0时线性表是一个空表。若用L命名线性表,则其一般表示为)
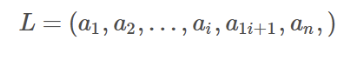
- 特点:
- 存在惟一的第一个元素。
- 存在惟一的最后一个元素。
- 除第一个元素之外,每个元素均只有一个直接前驱。
- 除最后一个元素之外,每个元素均只有一个直接后继
- 几个概念:
- ai是线性表中的“第i个”元素线性表中的位序。
- a1是表头元素;an是表尾元素。
- 除第一个元素外,每个元素有且仅有一个直接前驱:除最后一个元素外,每个元素有且仅有一个直接后继。
- 存储结构:
- 顺序存储结构:顺序表
- 链式存储结构:链表
2.1.2 线性表的基础操作
| InitList(&L) | 初始化表。构造一个空的线性表L, 分配内存空间。 |
|---|---|
| DestroyList(&L) | 销毁操作。销毁线性表,并释放线性表L所占用的内存空间 |
| ListInsert(&L;i,e) | 插入操作。在表L中的第i个位置上插入指定元素e。 |
| ListDelete(&L,i,&e) | 删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值 |
| LocateElem(L,e) | 按值查找操作。在表L中查找具有给定关键字值的元素。 |
| GetElem(L,i) | 按位查找操作。获取表L中第i个位置的元素的值 |
| Length(L) | 求表长。返回线性表L的长度,即L中数据元素的个数 |
| PrintList(L) | 输出操作。按前后顺序输出线性表L的所有元素值 |
| Empty(L) | 判空操作。若L为空表,则返回true,否则返回false |
“&“是C++的用法,表示引用。是否要传入引用”&“取决于对参数的修改结果是否需要”带回来”
void test(int x) {
x = 1024;
printf("test函数内部x = %d\n", x);
}
int main() {
int x = 1;
printf("调用test前 x = %d\n", x);
test(x);
printf("调用test后 x = %d\n", x);
return 0;
} void test(int& x) {
x = 1024;
printf("test函数内部x = %d\n", x);
}
int main() {
int x = 1;
printf("调用test前 x = %d\n", x);
test(x);
printf("调用test后 x = %d\n", x);
return 0;
}小结
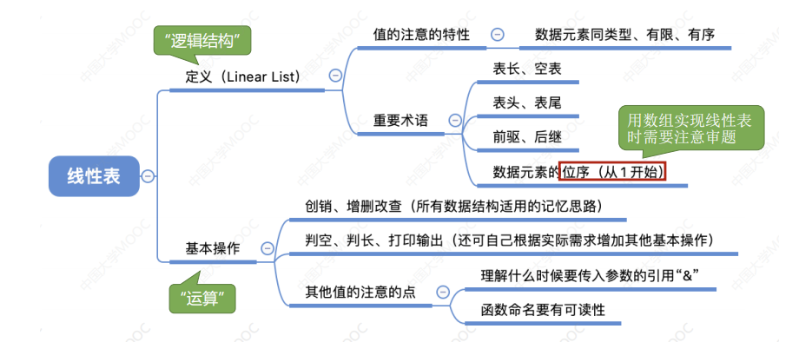
2.2 顺序表
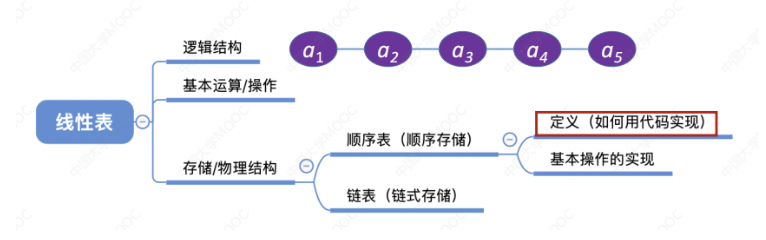
2.2.1 顺序表的定义
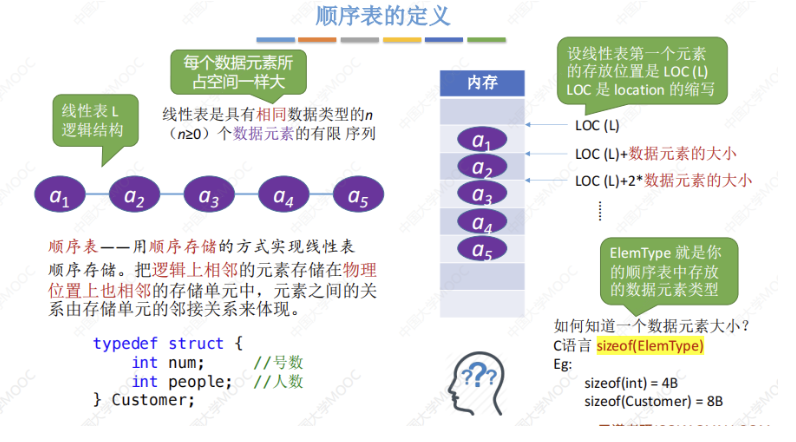
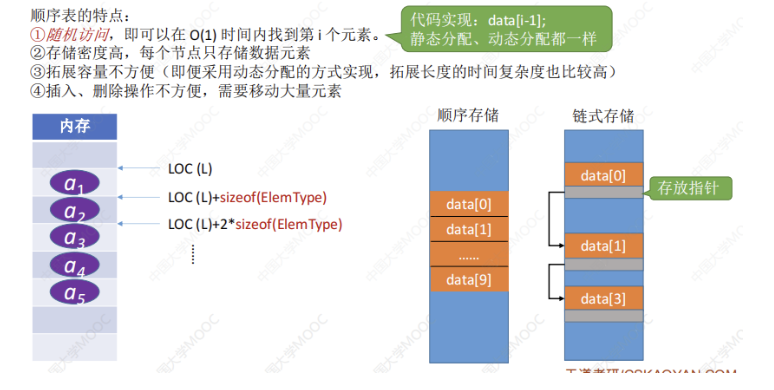
2.2.2. 顺序表的实现
1.静态分配
#define MaxSize 10 //定义最大长度
typedef struct{
ElemType data[MaxSize]; //用静态的"数组"存放数据元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义(静态分配方式)
//基本操作——初始化一个顺序表
void InitList(SqList &L){
L.length=0; //顺序表初始长度为0
}声明一个顺序表时在内存中分配存储顺序表L的连续空间。包括:MaxSize×sizeof(ElemType)和存储Length的空间
初始化顺序表时可以不用把各个数据元素的值设为默认值,直接将Length的值设为0即可。尽管内存中会有遗留的”脏数据”,但是因为访问超过当前长度的值是违法的,所以并不会有什么影响
尽量使用基本操作来访问顺序表中的各个数据元素
2.动态分配
因为静态分配实现的顺序表的表长开始确定后就无法更改(存储空间是静态的),刚开始就声明一个很大的内存空间又很浪费。所以可以用动态分配的方式实现顺序表大小可变
#define InitSize 10 //顺序表的初始长度
typedef struct{
ElemType *data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList; //顺序表的类型定义(动态分配方式)C提供了malloc和free函数来实现动态申请和释放内存空间。使用时加头文件#include<stdlib.h>。 malloc函数会申请一整片连续的存储空间,返回指向这片存储空间开始地址的指针。需要强制转型来决定这片存储空间用来存储什么类型的数据元素。如L.data=(ElemType *)malloc(sizeof(ElemType) * InitSize)就强制转型为了你定义的数据元素类型指针,并让data指针变量指向这一整片存储空间的起始地址也就是顺序表的第一个数据元素。
C++可以用new和delete关键字实现类似与malloc和free的功能,但要涉及到面向对象的一些相关知识
实现初始化顺序表和增加动态数组的长度
#include<stdlib.h>
#define InitSize 10 //默认的最大长度
typedef struct{
int* data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList;
void InitList(SeqList &L){
//用malloc函数申请一片连续的存储空间
L.data=(int*)malloc(InitSize*sizeof(int));
L.length=0;
L.MaxSize=InitSize;
}
//增加动态数组的长度
void IncreaseSize(SeqList &L,int len){
int *p=L.data;
L.data=(int*)malloc((L.MaxSize+len))*sizeof(int));
for(int i=0;i<L.length;i++){
L.data[i]=p[i]; //将数据复制到新区域
}
L.MaxSize=L.MaxSize+len; //顺序表最大长度增加len
free(p); //释放原来的内存空间
}
int main(){
SeqList L; //声明一个顺序表
InitList(L); //初始化顺序表
//...往顺序表中随便插入几个元素...
IncreaseSize(L,5);
return 0;
}小结
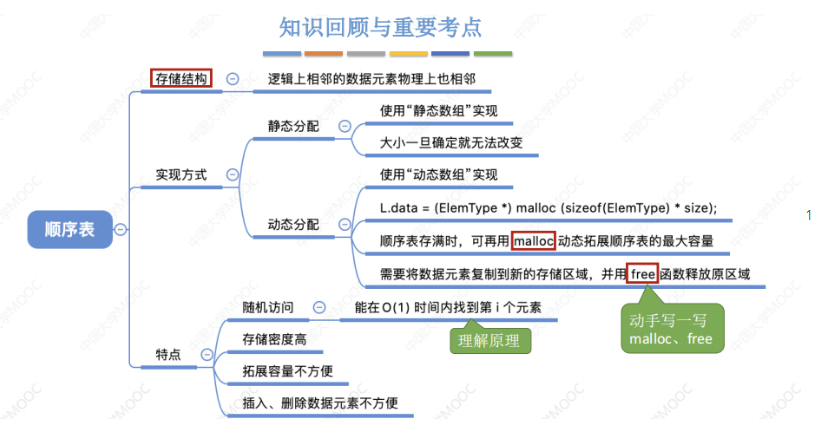
2.2.3 顺序表的基本操作
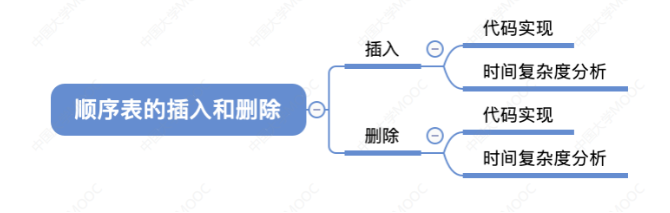
1.插入
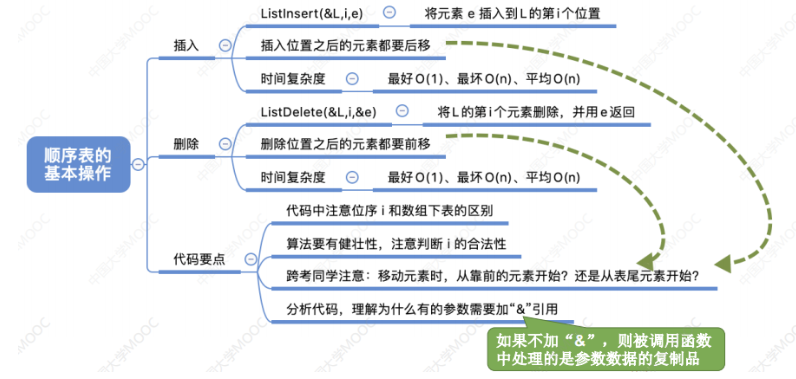
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e
要把第i个位置开始的n-i+1个元素全部后移一位,再在第i个位置上填入要插入的元素e
#define MaxSize 10 //定义最大长度
typedef struct{
int data[MaxSize]; //用静态的"数组"存放数组元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize) //当前存储空间已满,不能插入
return false;
for(int j=L.length;j>=i;j--) //将第i个元素及之后的元素后移
L.data[j]=L.data[j-1]; //注意位序,数组下标的关系,并从后面的元素依次移动
L.data[i-1]=e; //在位置i处放入e
L.length++; //长度加1
return true;
}
分析时间复杂度,关注最深处循环语句的执行次数与问题规模n的关系。这里的问题规模n=L.length(表长)
最好情况:新元素插入到表尾,不需要移动元素 i=n+1,循环0次;最好时间复杂度=O(1) 最坏情况:新元素插入到表头,需要将原有的n个元素全部向后移动 i=1,循环n次;最坏时间复杂度=O(n) 平均情况:假设新元素插入到任何一个位置的概率相同,即i=1,2,3,…,length+1的概率都是p = 1/(n + 1)
i=1,循环n次;i=2时,循环n-1次 … i=n+1时,循环0次。平均循环次数=np+(n-1)p+(n-2)p+…+1⋅p=n/2,故平均时间复杂度为O(n)
2.删除
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值
bool ListDelete(SqList &L,int i,int &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e=L.data[i-1]; //将被删除的元素赋值给e
for(int j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j]; //注意位序,数组下标的关系,并从后面的元素依次移动
L.length--; //线性表长度减1
return true;
}
删除时是先移动前面的元素再移动后面的元素,插入操作时则是先移动后面的元素再移动前面的元素
仿造对插入操作的时间复杂度分析可得删除操作的时间复杂度:
最好情况:删除表尾元素,不需要移动其他元素 i=n,循环0次;最好时间复杂度=O ( 1 ) 最坏情况:删除表头元素,需要将后续的n-1个元素全都向前移动 i=1,循环n-1次;最坏时间复杂度=O ( n )
平均情况:假设删除任何一个元素的概率相同,即i=1,2,3,…,length的概率都是p = 1/n
i=1,循环n-1次;i=2时,循环n-2次;i=3,循环n-3次 … i=n时,循环0次。平均循环次数=(n-1)p+(n-2)p+…+1⋅p=(n-1)/2,故平均时间复杂度为O(n)
插入与删除
3.查找
1)按位查找
GetElem(L,i) 按位查找操作。获取表L中第i个位置的元素的值
不管是采用静态分配的还是动态分配,都可以用如下方式实现按位查找
ElemType GetElem(SqList L,int i){
return L.data[i-1];
}只有一个return语句,没有递归调用也没有循环,时间复杂度为O(1)
由于顺序表的各个数据元素在内存中连续存放,因此可以根据起始地址和数据元素大小立即找到第i个元素。这就是顺序表的“随机存取”特性
2)按值查找
LocateElem(L,e) 按值查找操作。在表L中查找具有给定关键字值的元素
同样不管是采用静态分配的还是动态分配,都可以用如下方式实现按值查找
//在顺序表L中查找第一个元素值等于e的元素,并返回其位序
int LocateElem(SeqList L,int e){
for(int i=0;i<L.length;i++)
if(L.data[i]==e)
return i+1;
return 0;
}
这里是假定顺序表存储的数据类型为int,如果类型是结构体,判断相等不能直接用“==”。判断相等时如果是C语言要自己写,C++还可以用运算符重载
现在分析时间复杂度。最好情况是目标元素在表头,最好时间复杂度为O(1)。最坏情况是目标元素在表尾,最坏时间复杂度为O(n)。平均时间复杂度为O(n)
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客



