一、重要知识点
1.1 分段复合函数的计算

关键点:画内层函数图像,数形结合
1.2 ∞-∞ 采用倒带换
1.3 泰勒展开式
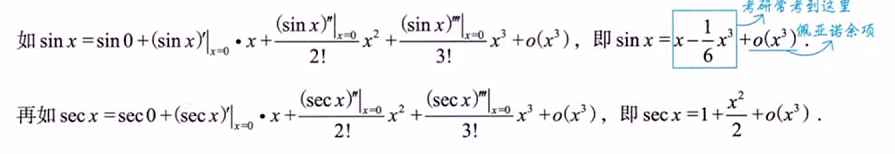

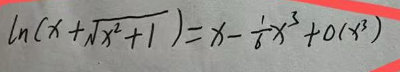
无穷级数
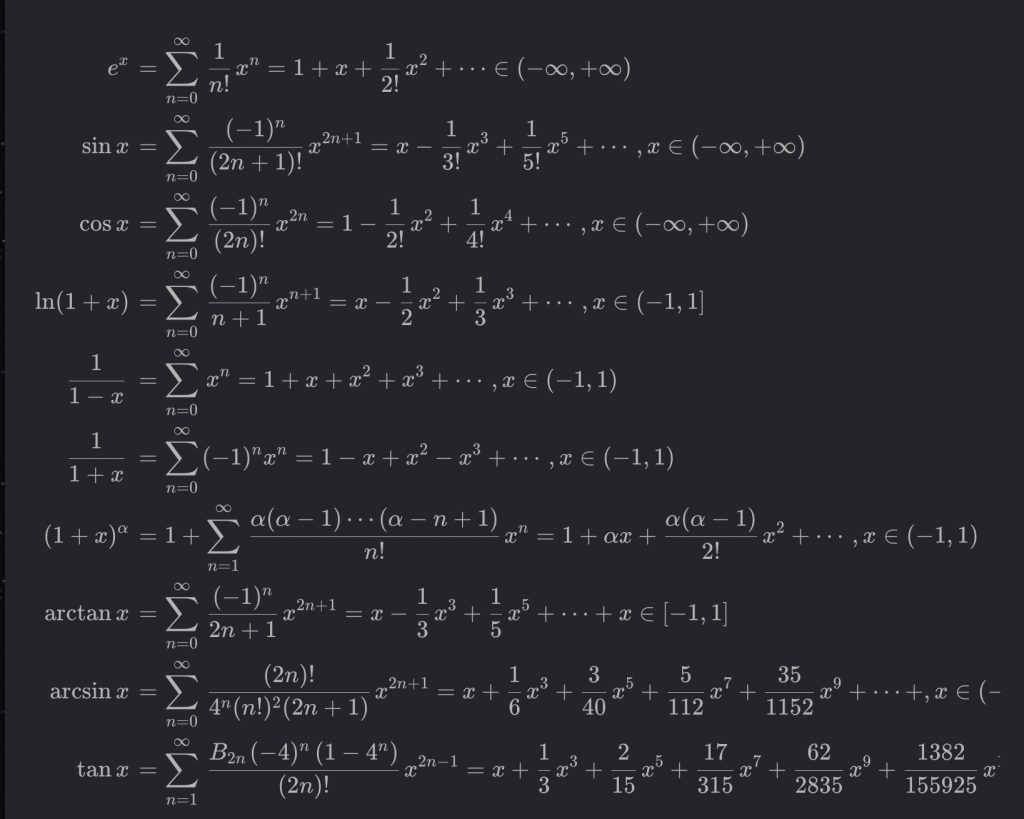
1.4 无穷小加减替换关系

1.5 无穷大速度的比较

1.6 基本公式&&无穷小公式总结

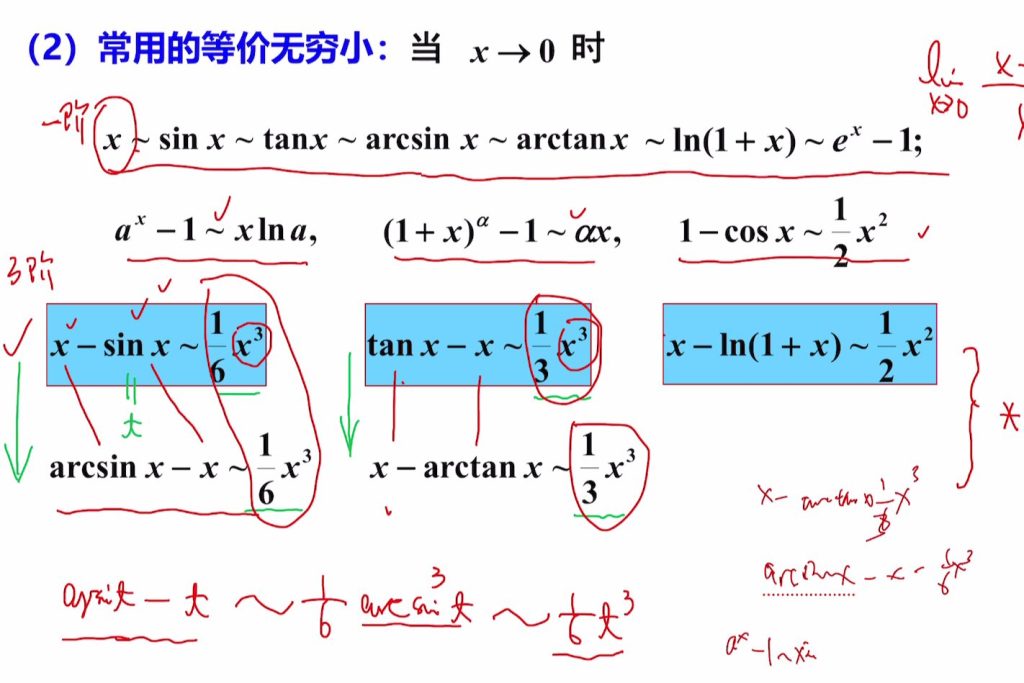


1.7 无穷小的运算

1.8 计算极限需要分左右极限

1.9 取整函数的性质与应用

1.10 什么时候能用洛必达

1.11 洛必达能洛几次的问题
如果f(x)在x的n阶导数连续

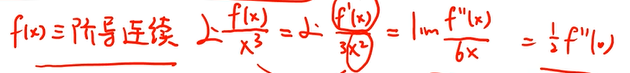


如果 f(x)在x有n阶导数(没说n 阶导函数连续)




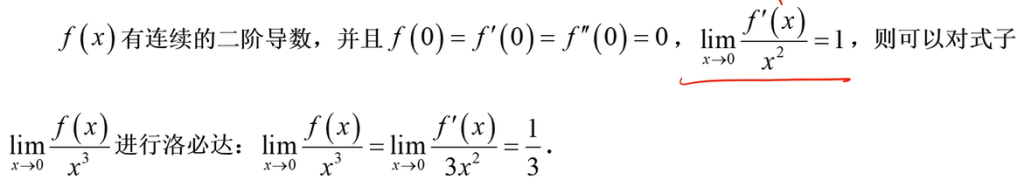
例题
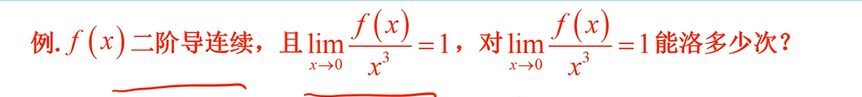
一次不能洛

选A
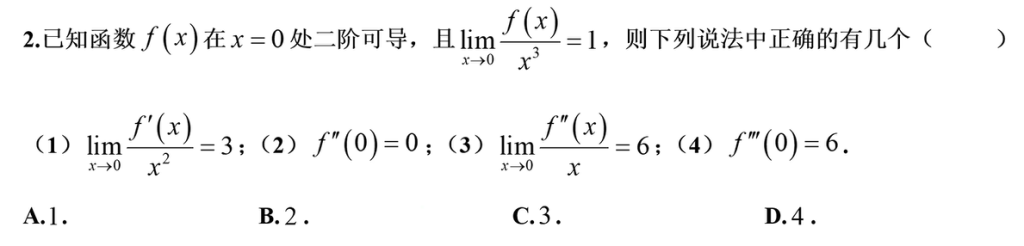
1.12 利用定积分求极限

什么时候用定积分、什么时候用夹逼

定积分定义计算极限,三部曲

1.13 证明单调有界的方法(重点)
方法一

证明单调的常用方法

证明数列有界的方法


方法二 递推函数法


方法三:压缩映射法



1.14 分段函数求导

1.15 曲率公式

二 习题
1 分段复合函数
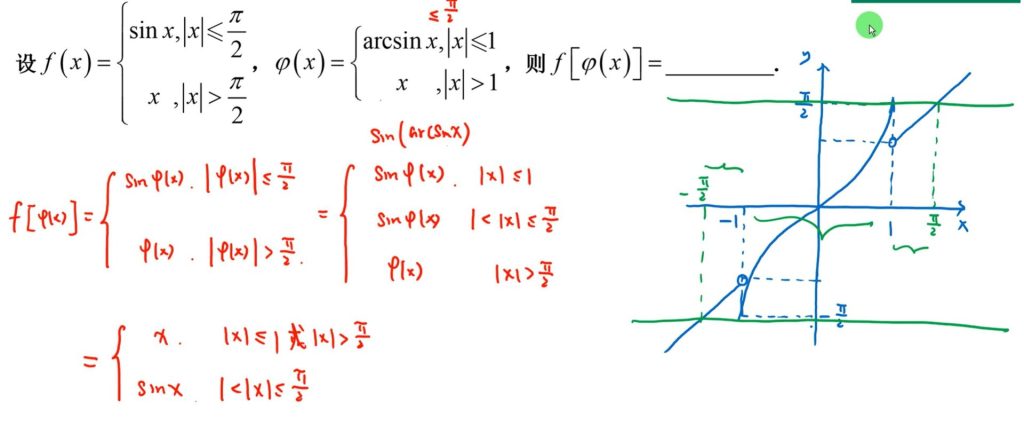
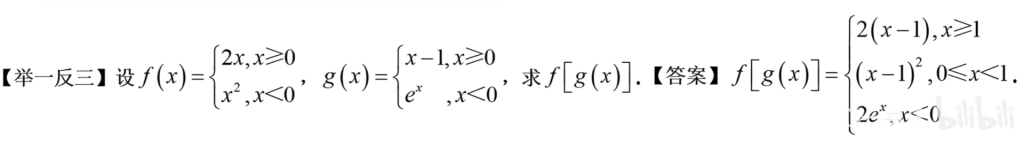
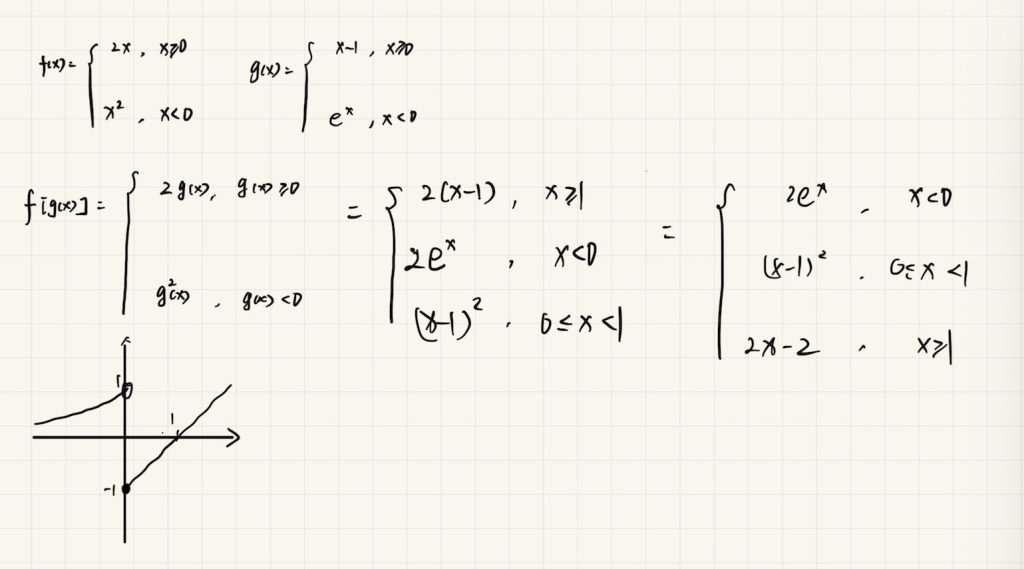
2 计算分段复合函数求极限

特别注意 方法二、f(x) 不等于0
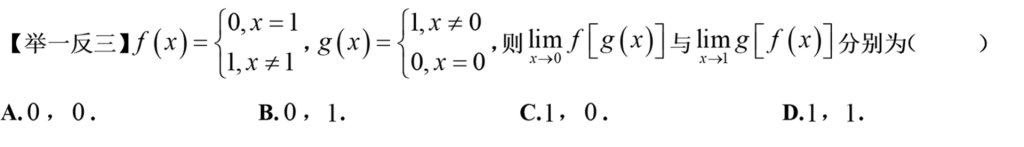

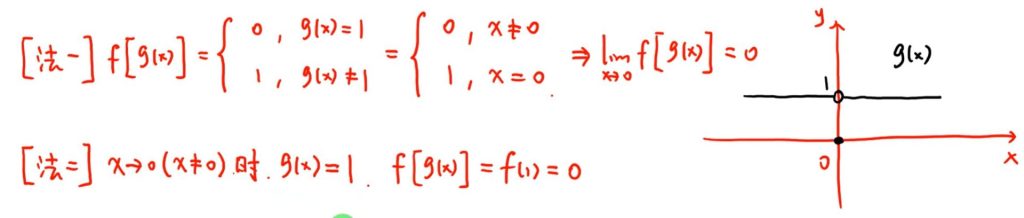
3 自变量的广义化
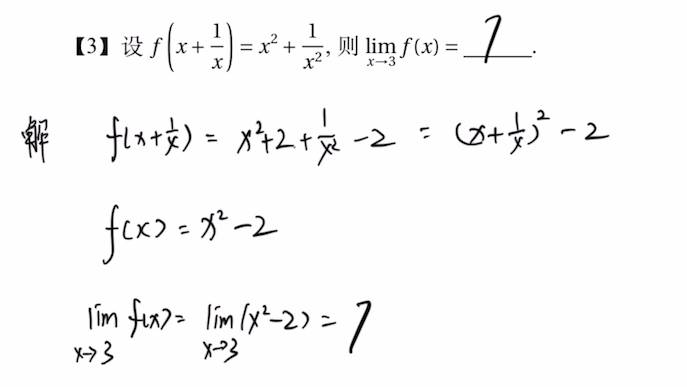
举一反三
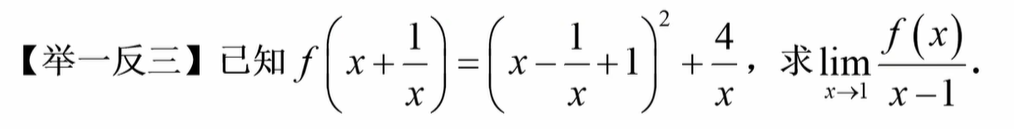
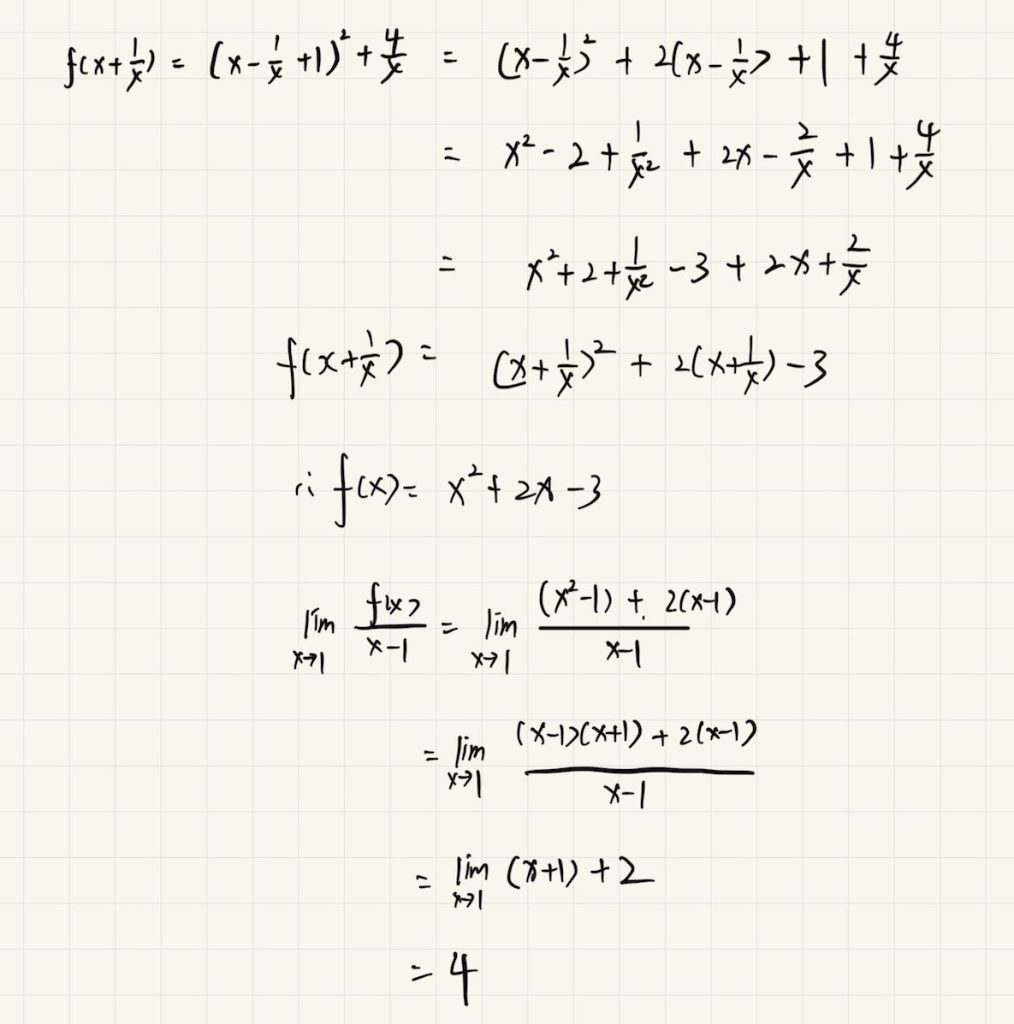
4 极限和无穷小的关系
方法一

方法二

5 已知极限求极限
方法一
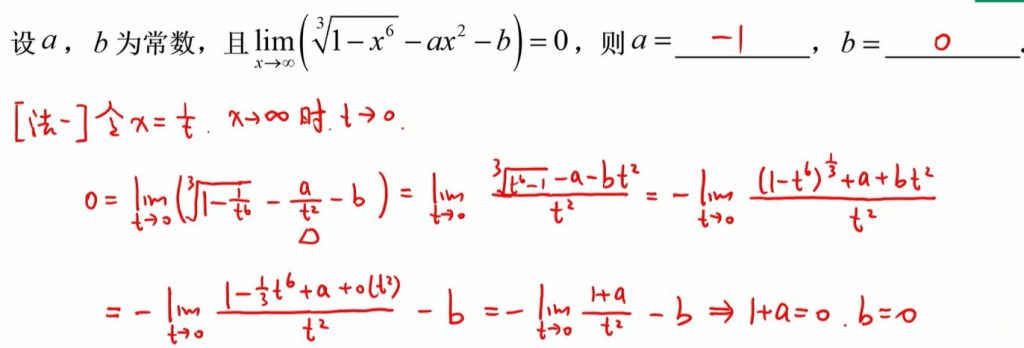
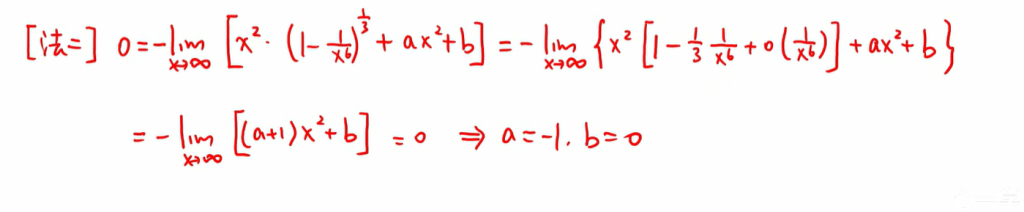
举一反三题
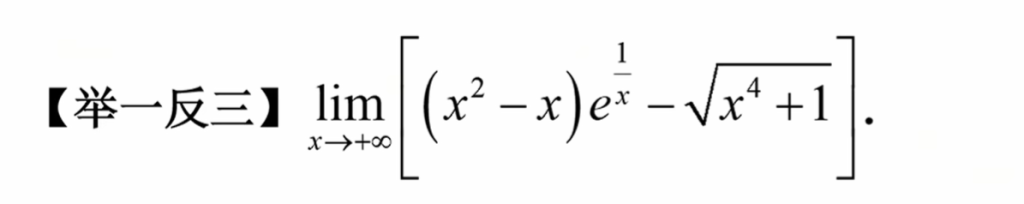

这里泰勒展开需要展开到第三项,为了减小误差
6 极限0/0型
方法一:看到根号 – 有理化
方法二:利用+1 – 1 化简
方法三:拉格朗日
方法四:泰勒公式

7 无穷大速度的比较

8 关于 uv 类型求极限
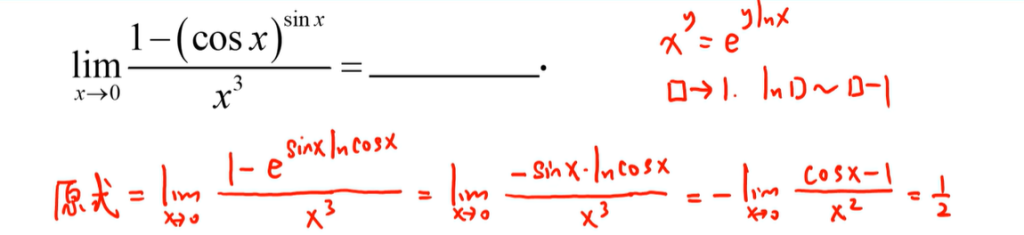
9 极限 a 的+∞ 分类讨论

10 极限连续问题

11 极限计算(易错题)
易错点:泰勒展开的地步
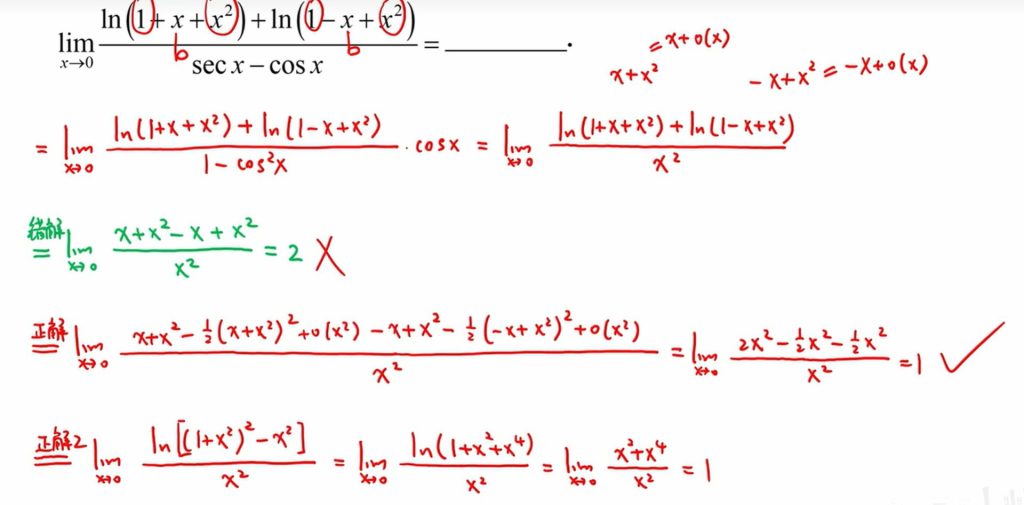
12 泰勒展开 – 深入理解

改 成x5

举一反三
13 易错
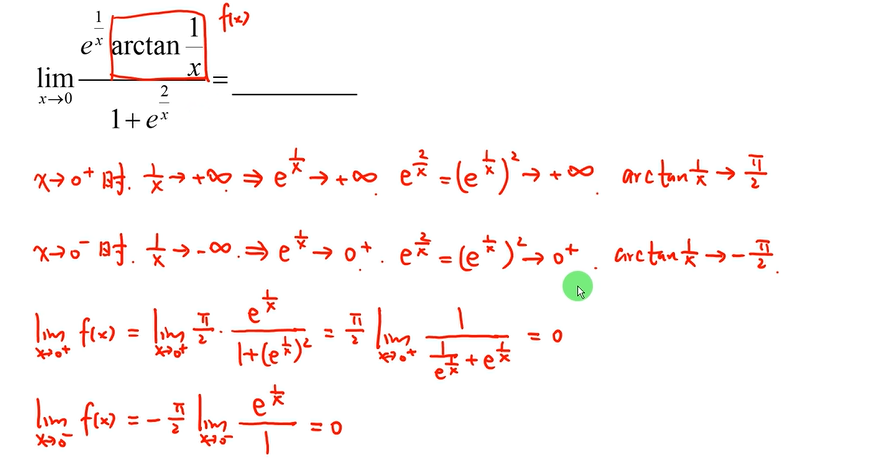
14 取整函数

15 极限 抽象
泰勒公式
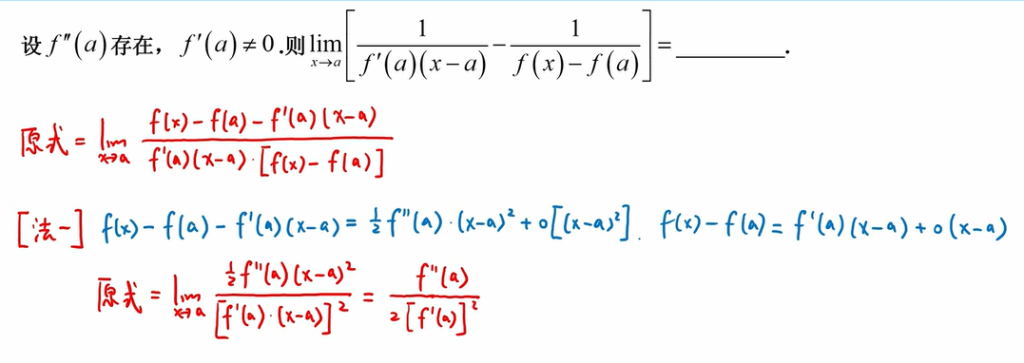
洛必达
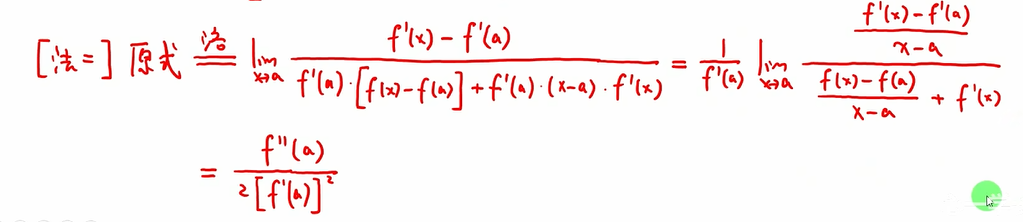



16 极限为常数

17 定积分定义

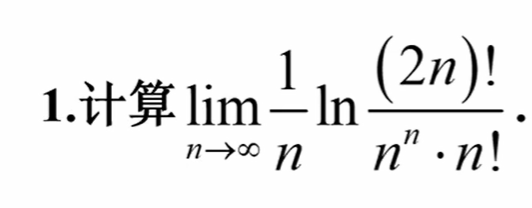
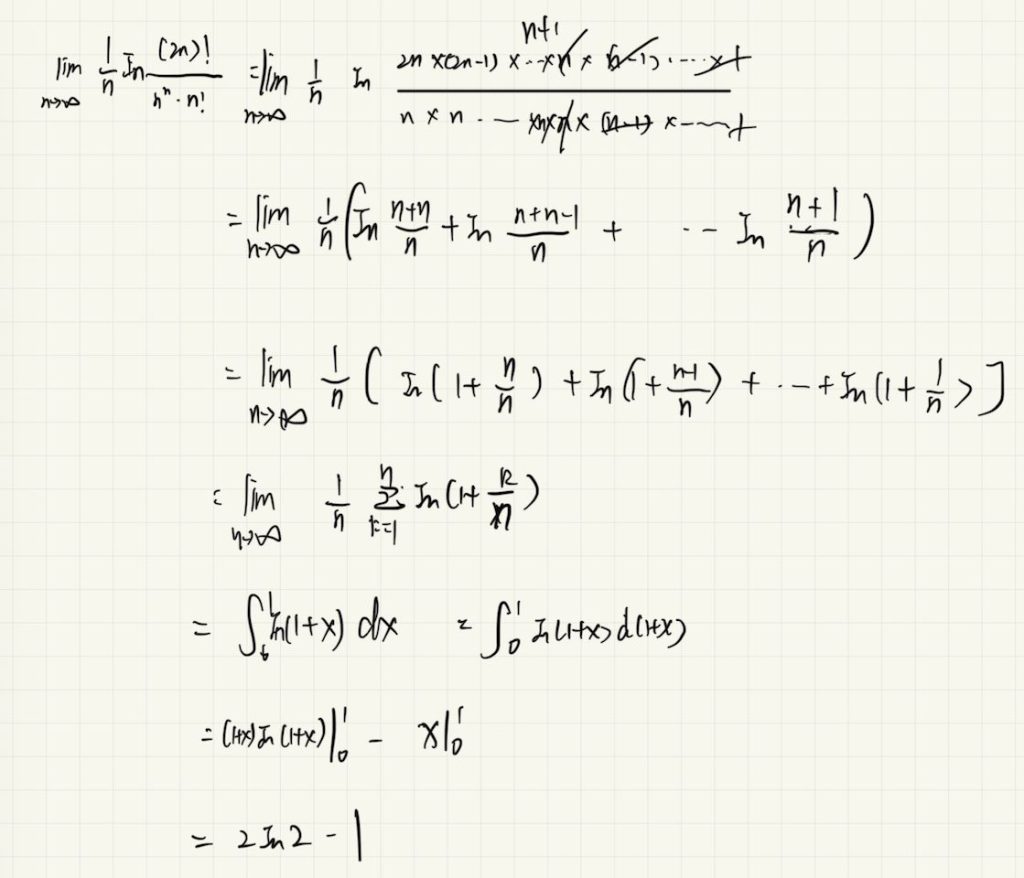
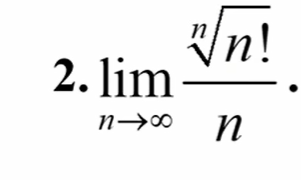

18 含有递推式数列极限证明
方法一:单调有界

卡bug也适用于填空题
证明单调最无敌的方法(适用于所有方法)

方法二:压缩映射法(使用范围更广,即可以搞单调,也可以搞不单调的)
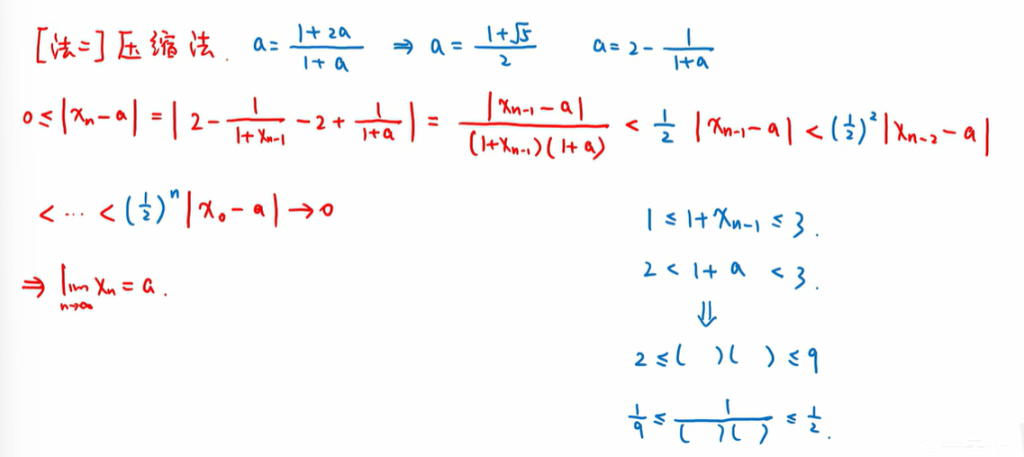
举一反三
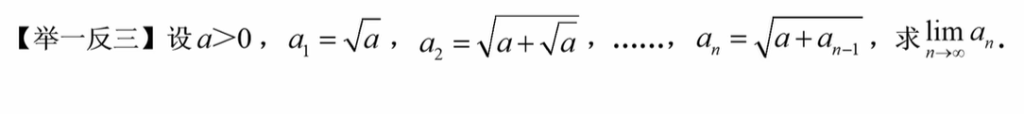
方法一:

方法二:

19 极限定义的分段函数

20 间断点

21 分段函数求导

22 利用导数定义求极限
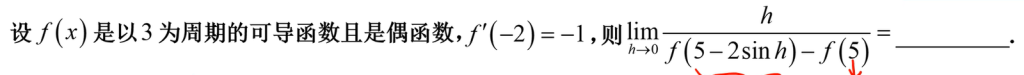
错解

正解
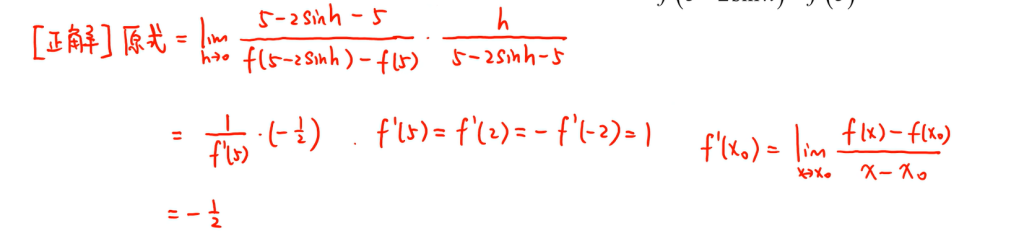


23 幂指函数求导

24 参数方程及曲率
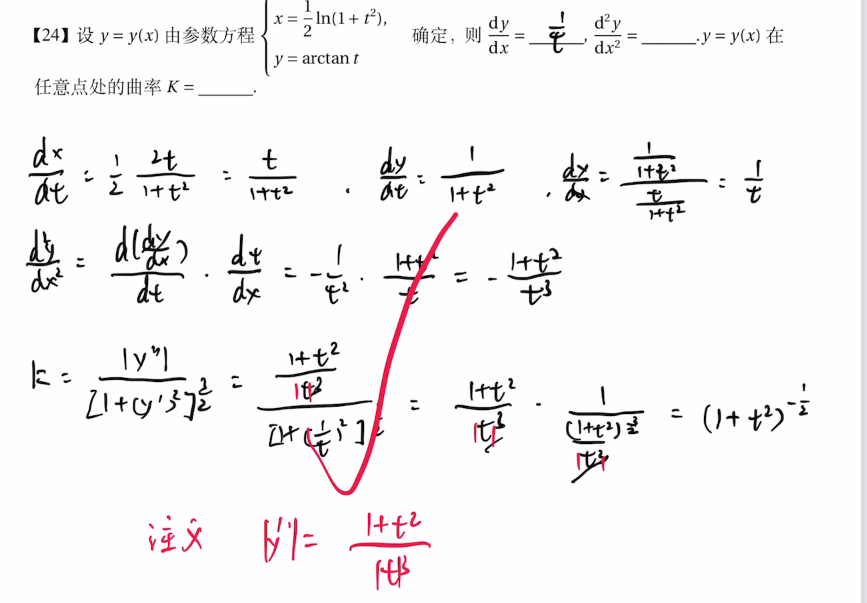
24 数三

【举一反三】

25 求微分 – 细节
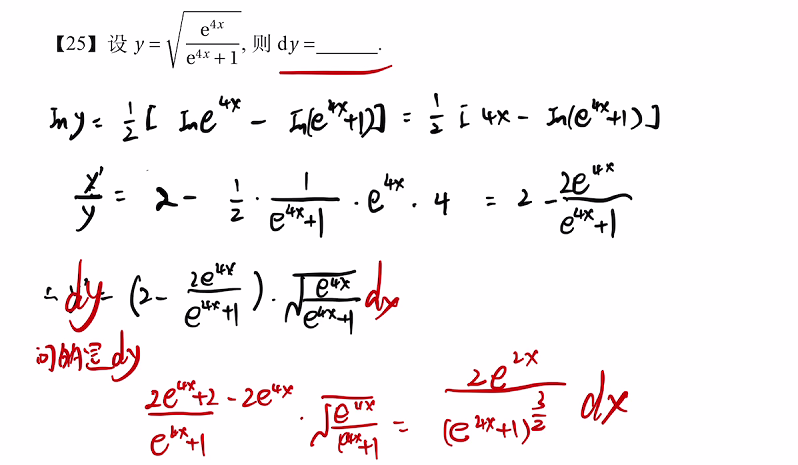
26 泰勒公式对比系数
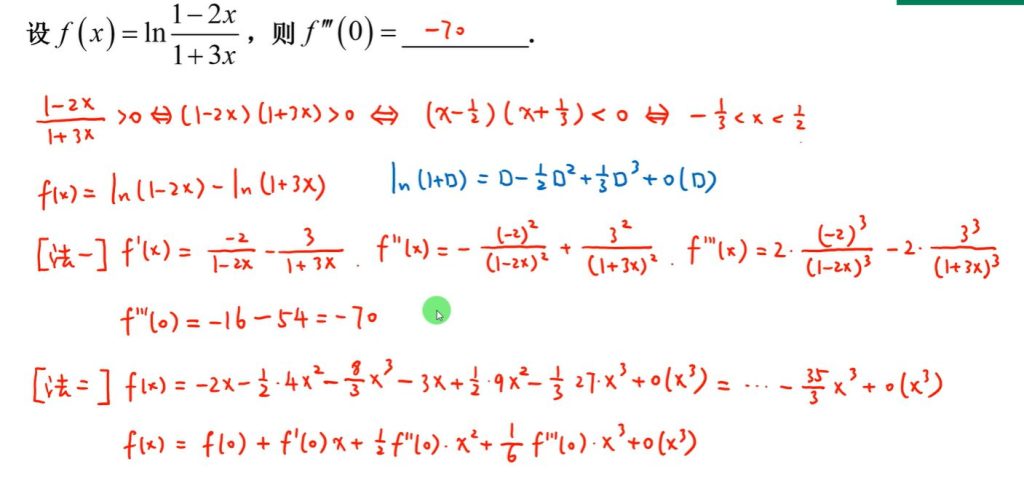
【举一反三】

27 切线方程

28 法线方程

29 切线方程

30 确定区间

31 拐点
二阶导等于0,三阶导不等于0

32 已知可导求参数

33 分段函数的导数

34 导数定义求极限 陷阱题



35 导数定义求极限

36

37 难题,大题思路


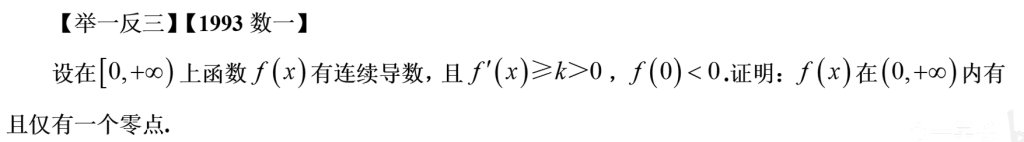
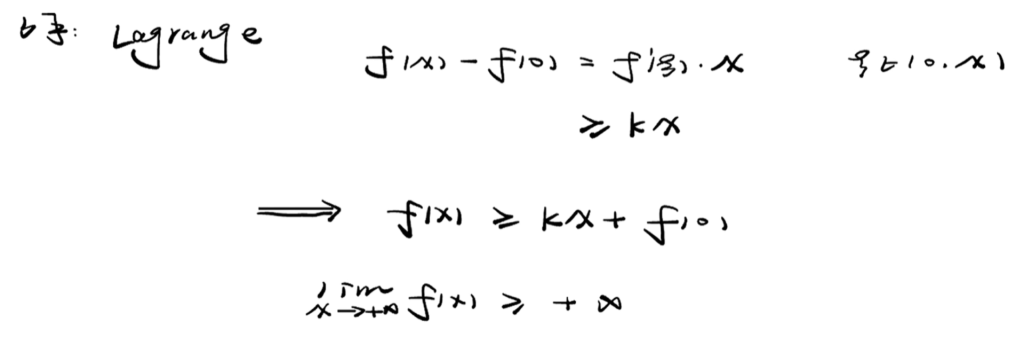


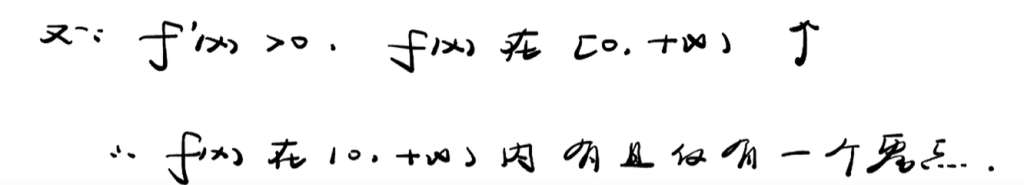

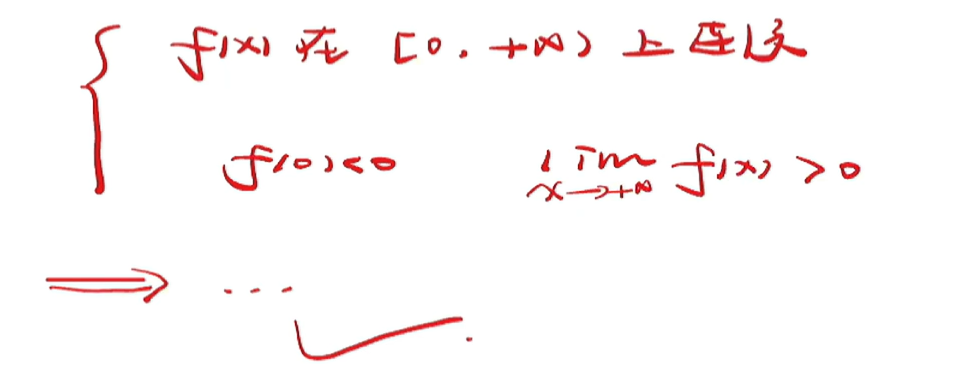
38 求驻点

39

三 错误题目
| 题号(类型) | 备注 |
| 1 | 计算分段复合函数 |
| 5 | 泰勒公式的记忆 |
| 11 | 计算错误 |
| 12 | 计算不会 |
| 14 | 取整函数 |
| 15 | 洛必达的应用 |
| 17 | 定积分 |
| 18 | 带递推公式 |
| 19 | 讨论局部极限 |
| 21 | 分段函数求导 |
| 22 举一反三 | 利用导数定义求极限 |
| 26 泰勒公式对比系数 | |
| 33 分段函数的导数 | 注意分段函数求导 |
| 34 导数定义求极限 | |
| 35 导数定义求极限 | |
| 37 | |
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客


