一、操作符分类
1、算术操作符
2、移位操作符
3、位操作符
4、赋值操作符
5、单目操作符
6、关系操作符
7、逻辑操作符
8、条件操作符
9、逗号操作符
10、下标引用、函数调用和结构成员
二、算术操作符
1、+
2、-
3、*
4、/
5、%
结论:
除了%操作符,其他的操作符可以作用于整数和浮点数
对于 / 操作符如果两个操作数都为整数,执行整数除法。而只要有浮点数执行的就是浮点数除法
% 操作符的两个操作数必须为整数。返回的是整数之后的余数
三、移位操作符
移位操作符 – 移动的是内存中的补码
左移动,右移动操作符只针对整数
警告:对于移位操作符,不要移动负数位,这个是标准未定义的
例如:
int num = 10; num >> -1;//error
3.1 原码、反码、补码
正的整数的原码、反码、补码相同
以整数 7 为例
负的整数的原码、反码、补码是要计算的
以整数 -7 为例
整数在内存中存储的是补码
3.2 左移操作符
左移操作符移动的是二进制位
3.2.1 正数的左 移位操作
#include <stdio.h>
int main()
{
int a = 7;
int b = a << 1;
printf("a = %d\n", a);
printf("b = %d\n", b);
return 0;
}运算结果:
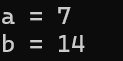
左移操作符计算规则:左边丢弃、右边补0

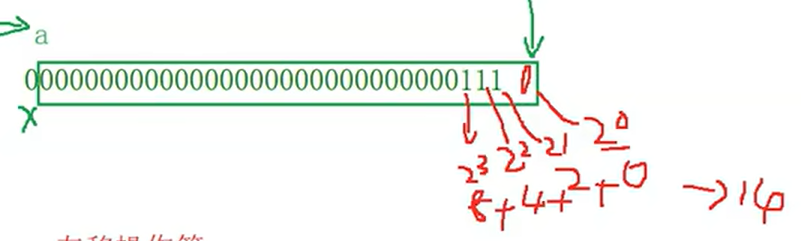
3.2.2 负数的移位操作
代码实现
#include <stdio.h>
int main()
{
int a = -7;
int b = a << 1;
printf("a = %d\n", a);
printf("b = %d\n", b);
return 0;
}运行结果
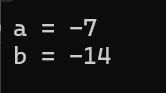
运行原理
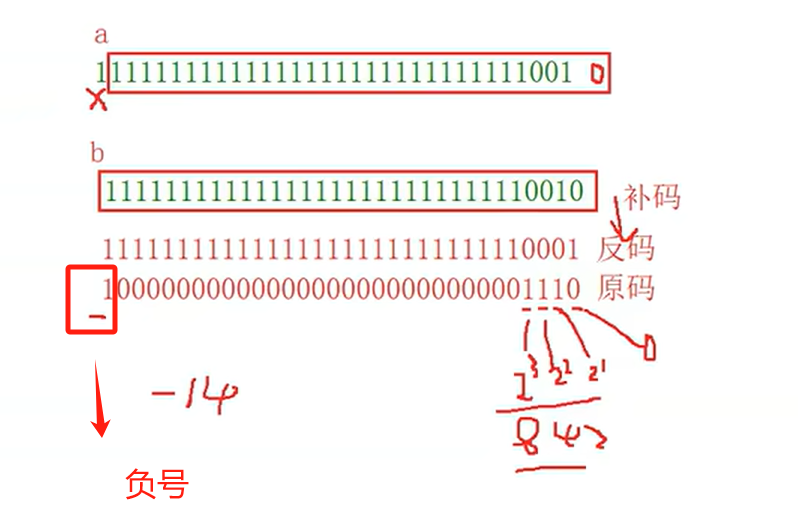
3.3 右移操作符
右移操作符分为:算术移位、逻辑移位
移位规则
算术移位:右边丢弃,左边补原符号位
逻辑移位:右边丢弃,左边补0
3.3.1 正数的右移位操作
代码实现
int main()
{
int a = 7;
int b = a >> 1;
printf("a = %d\n", a);
printf("b = %d\n", b);
return 0;
}运行结果
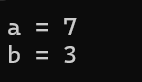
运行原理

结论:对于正数来说,判别不出编译器是算术右移还是逻辑右移,补0即可
3.3.2 负数的右移位操作
代码实现
int main()
{
int a = -7;
int b = a >> 1;
printf("a = %d\n", a);
printf("b = %d\n", b);
return 0;
}运行结果
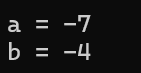
实现原理
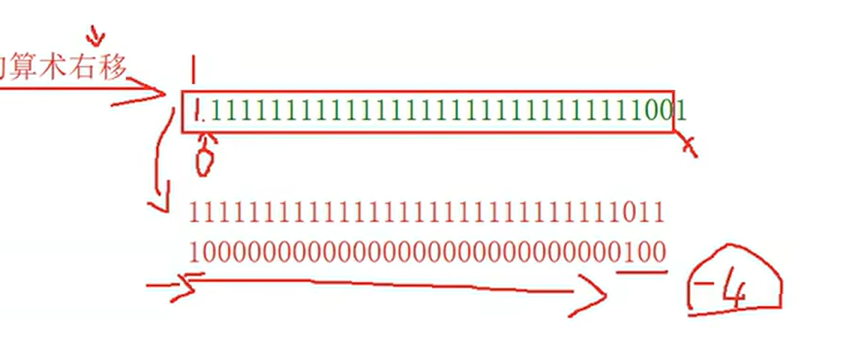
结论:
VS编译器 – 支持算术右移动
大多数编译器支持算术右移
四、位操作符
位操作符有:
& 按(2进制)位与
| 按(2进制)位或
^ 按(2进制)位异或
注:他们的操作数必须是整数
4.1 按位与 – &
代码实现
int main()
{
int a = 3;
int b = -5;
int c = a & b;
// 00000000 00000000 00000000 00000011 - 3的原码(正数 - 原码反码补码相同)
// 10000000 00000000 00000000 00000101 - -5的原码
// 11111111 11111111 11111111 11111010 - -5的反码
//
// 11111111 11111111 11111111 11111011 - -5的补码
// 00000000 00000000 00000000 00000011 - 3的补码
// 00000000 00000000 00000000 00000011 - 按位&之后的结果
// %d 意味着打印一个有符号的整数
printf("c = %d\n", c);
return 0;
}运行结果
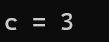
按位与原理
// 00000000 00000000 00000000 00000011 – 3的原码(正数 – 原码反码补码相同)
// 10000000 00000000 00000000 00000101 – -5的原码
// 11111111 11111111 11111111 11111010 – -5的反码
//
// 11111111 11111111 11111111 11111011 – -5的补码
// 00000000 00000000 00000000 00000011 – 3的补码
// 00000000 00000000 00000000 00000011 – 按位&之后的结果
4.2 按位或 – |
代码实现
int main()
{
int a = 3;
int b = -5;
int c = a | b;
// 00000000 00000000 00000000 00000011 - 3的原码(正数 - 原码反码补码相同)
// 10000000 00000000 00000000 00000101 - -5的原码
// 11111111 11111111 11111111 11111010 - -5的反码
//
// 11111111 11111111 11111111 11111011 - -5的补码
// 00000000 00000000 00000000 00000011 - 3的补码
// 11111111 11111111 11111111 11111011 - 按位|之后的结果 - 补码
// 11111111 11111111 11111111 11111010 - 减1
// 10000000 00000000 00000000 00000101 - 取反(除去第一位的符号,其他的都反)
//
// %d 意味着打印一个有符号的整数
printf("c = %d\n", c);
return 0;
}运行结果
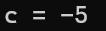
按位或原理
// 00000000 00000000 00000000 00000011 – 3的原码(正数 – 原码反码补码相同)
// 10000000 00000000 00000000 00000101 – -5的原码
// 11111111 11111111 11111111 11111010 – -5的反码
// 11111111 11111111 11111111 11111011 – -5的补码
// 00000000 00000000 00000000 00000011 – 3的补码
// 11111111 11111111 11111111 11111011 – 按位|之后的结果 – 补码
// 11111111 11111111 11111111 11111010 – 减1
// 10000000 00000000 00000000 00000101 – 取反(除去第一位的符号,其他的都反)
// %d 意味着打印一个有符号的整数
4.3 按位异或 – ^
相同为0,相异为1
a^a = 0
0^a = a
异或支持交换律
代码实现
int main()
{
int a = 3;
int b = -5;
int c = a ^ b;
// 00000000 00000000 00000000 00000011 - 3的原码(正数 - 原码反码补码相同)
// 10000000 00000000 00000000 00000101 - -5的原码
// 11111111 11111111 11111111 11111010 - -5的反码
//
// 11111111 11111111 11111111 11111011 - -5的补码
// 00000000 00000000 00000000 00000011 - 3的补码
// 11111111 11111111 11111111 11111000 - 按位^之后的结果 - 补码
//
// 11111111 11111111 11111111 11110111 - 减1
// 10000000 00000000 00000000 00001000 - 取反(除去第一位的符号,其他的都反)
//
// %d 意味着打印一个有符号的整数
printf("c = %d\n", c);
return 0;
}运行结果
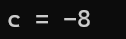
按位异或原理
00000000 00000000 00000000 00000011 – 3的原码(正数 – 原码反码补码相同)
10000000 00000000 00000000 00000101 – -5的原码
11111111 11111111 11111111 11111010 – -5的反码11111111 11111111 11111111 11111011 – -5的补码
00000000 00000000 00000000 00000011 – 3的补码
11111111 11111111 11111111 11111000 – 按位^之后的结果 – 补码11111111 11111111 11111111 11110111 – 减1
10000000 00000000 00000000 00001000 – 取反(除去第一位的符号,其他的都反)
4.4 位操作符的应用
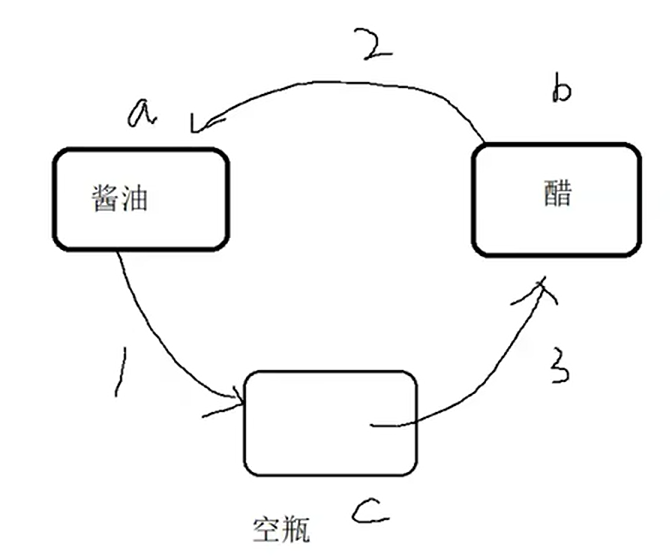
4.4.1 题目:不能创建临时变量(第三个变量),实现两个数的交换。
创建临时变量的方法(开发中一般采用的方法,效率高,可读性强)
int main()
{
int a = 3;
int b = 5;
int c = 0;
c = a;
a = b;
b = c;
printf("a = %d b = %d\n", a,b);
return 0;
}方法1 – 该方法会有溢出的问题
int main()
{
int a = 3;
int b = 5;
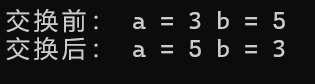
printf("交换前: a = %d b = %d\n", a, b);
a = a + b;
b = a - b;
a = a - b;
printf("交换后: a = %d b = %d\n", a, b);
return 0;
}运行结果:
方法2 – 采用异或的方法
int main()
{
int a = 3;
int b = 5;
printf("交换前: a = %d b = %d\n", a, b);
a = a ^ b; // 3^5
b = a ^ b; // 3^5^5 = 3^0 = 3
a = a ^ b; // 3^5^3 = 5^0 = 5
printf("交换后: a = %d b = %d\n", a, b);
return 0;
}
// 3^3 = 0 -> a^a = 0
// 011 =
// 011 =
// 000
// 0^5 = 5 - > 0^a = a
// 000
// 101
// 101
// 3^3^5 = 5
// 3^5^3 = 5 - 异或支持交换律
// 011
// 101
// 011
// 101代码原理(重点)
异或 符合交换律
a = a ^ b; // 3^5
b = a ^ b; // 3^5^5 = 3^0 = 3
a = a ^ b; // 3^5^3 = 5^0 = 5
推理
// 3^3 = 0 -> a^a = 0
// 011 =
// 011 =
// 000// 0^5 = 5 – > 0^a = a
// 000
// 101
// 101// 3^3^5 = 5
// 3^5^3 = 5 – 异或支持交换律
// 011
// 101
// 011
// 101
4.4.2 题目:编写代码实现:求一个整数存储在内存中的二进制中的 1 的个数
求补码中二进制中 1 的个数
int a = 3;
00000000000000000000000000000011 – 3 的补码
a & 1
00000000000000000000000000000011
00000000000000000000000000000001
00000000000000000000000000000001
方法1
int main()
{
int num = 10;
int count = 0;
while (num)
{
if (num % 2 == 1)
{
count++;
}
num = num / 2;
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}方法2:
int main()
{
int num = 10;
int i = 0;
int count = 0;
for(i = 0;i<32;i++)
{
if (num&(1<<i))
{
count++;
}
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}方法3
int main()
{
int num = -1;
int i = 0;
int count = 0;
while (num)
{
count++;
num = num & (num - 1);
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}Brian Kernighan 算法
#include <stdio.h>
int main() {
int a = 5;
unsigned int num = (unsigned int)a;
int count = 0;
while (num != 0) {
num &= (num - 1); // 消除最右的1
count++;
}
printf("count = %d\n", count);
return 0;
}我们以 a=5(二进制 00000101)为例,用二进制演示代码中 num &= (num - 1) 的操作原理:
初始状态num = 5(二进制:00000101,共 2 个 1)count = 0
第一次循环
计算 num - 1:num = 5 → 二进制 00000101num - 1 = 4 → 二进制 00000100(最右边的 1 变成 0,右侧所有 0 变 1)
执行 num &= (num - 1)(按位与):00000101(num)& 00000100(num-1)= 00000100(结果)
此时 num 变为 4(二进制 00000100),count 自增为 1(消除了最右边的 1)。
第二次循环
计算 num - 1:num = 4 → 二进制 00000100num - 1 = 3 → 二进制 00000011(最右边的 1 变成 0,右侧所有 0 变 1)
执行 num &= (num - 1):00000100(num)& 00000011(num-1)= 00000000(结果)
此时 num 变为 0,count 自增为 2(消除了最后一个 1)。
循环终止num 变为 0,循环结束。最终 count=2,正确统计了 5 的二进制中 1 的个数(00000101 有 2 个 1)。
核心原理总结num &= (num - 1) 的作用是消除二进制中最右边的 1:num - 1 会将最右边的 1 变为 0,并将其右侧所有 0 变为 1(例如 00000101 → 00000100)。
按位与操作(&)会将 num 中最右边的 1 及其右侧的所有位清零(例如 00000101 & 00000100 = 00000100)。
每执行一次该操作,num 中最右边的 1 就被消除,count 记录消除次数。当 num 变为 0 时,所有 1 已被消除,count 即为 1 的总个数。
扩展验证:负数场景
若 a=-1(32 位系统中二进制全 1):
初始 num = (unsigned int)(-1) = 0xFFFFFFFF(二进制 32 个 1)。
每次循环消除最右边的 1,共执行 32 次循环,最终 count=32(正确统计 32 个 1)。
该算法的时间复杂度为 O(k)(k 是二进制中 1 的个数),比逐位检查(O(32/64))更高效。
五、赋值操作符
在 C 语言中,赋值操作符的主要作用是将右侧表达式的值赋给左侧的变量(或内存空间),它是 C 语言中最基础的操作符之一。以下是详细讲解及代码示例:
5.1 基础赋值操作符(=)
最常用的赋值操作符是 =,语法格式为:变量 = 表达式;
它表示将右侧表达式的计算结果存储到左侧变量对应的内存空间中。
注意:
- 左侧必须是可修改的 “左值”(如变量、数组元素、结构体成员等),不能是常量或表达式(如
5 = a;或a+1 = 3;是非法的)。 - 赋值操作本身有返回值:赋值表达式的结果是左侧变量被赋值后的值,因此可以链式赋值(如
a = b = c = 0;)。
5.2 复合赋值操作符
为简化代码,C 语言提供了复合赋值操作符(共 10 种),适用于对变量进行 “运算 + 赋值” 的组合操作。
常见形式:变量 操作符= 表达式;(等价于 变量 = 变量 操作符 表达式;)。
| 操作符 | 等价形式 | 说明 |
|---|---|---|
+= | a = a + b | 加法后赋值 |
-= | a = a - b | 减法后赋值 |
*= | a = a * b | 乘法后赋值 |
/= | a = a / b | 除法后赋值(注意整除) |
%= | a = a % b | 取余后赋值(仅整数) |
<<= | a = a << b | 左移后赋值 |
>>= | a = a >> b | 右移后赋值 |
&= | a = a & b | 按位与后赋值 |
|= | a = a | b | 按位或后赋值 |
^= | a = a ^ b | 按位异或后赋值 |
5.3 代码实现
#include <stdio.h>
int main() {
int a, b = 5;
// 基础赋值操作
a = b; // a 被赋值为 b 的值(5)
printf("基础赋值:a = %d\n", a); // 输出:5
// 链式赋值
int x, y, z;
x = y = z = 10; // 等价于 z=10; y=z; x=y;
printf("链式赋值:x=%d, y=%d, z=%d\n", x, y, z); // 输出:10, 10, 10
// 复合赋值操作(以 +=、*= 为例)
a = 3;
a += 2; // 等价于 a = a + 2 → 3+2=5
printf("+= 操作后:a = %d\n", a); // 输出:5
a = 4;
a *= (b + 1); // 等价于 a = a * (b+1) → 4*(5+1)=24
printf("*= 操作后:a = %d\n", a); // 输出:24
// 其他复合赋值(以 %= 为例,仅整数)
int num = 13;
num %= 5; // 等价于 num = 13 % 5 → 3
printf("%%= 操作后:num = %d\n", num); // 输出:3(注意 %% 转义为 %)
return 0;
}

5.4 注意事项
- 赋值操作符的优先级较低(仅高于逗号操作符),使用时需注意结合顺序。例如
a = b + 3等价于a = (b + 3)。 - 复合赋值操作符会隐式限制变量类型(如
float类型使用%=会报错,因取余仅支持整数)。 - 赋值操作是 “写内存” 行为,频繁赋值可能影响性能(但现代编译器会优化)。
六、单目操作符
6.1 常见单目操作符分类及功能
1. 逻辑非 !
- 功能:对操作数的逻辑值取反(真变假,假变真)。
- 规则:操作数为 0(假)时结果为 1(真);非 0(真)时结果为 0(假)。
2. 按位取反 ~
- 功能:对操作数的二进制位逐位取反(1 变 0,0 变 1)。
- 注意:按位操作,与逻辑取反(
!)有本质区别。
3. 自增 ++ 和自减 --
- 功能:操作数自增 1(
++)或自减 1(--)。 - 区分:
- 前置形式(如
++a):先自增,再参与表达式运算。 - 后置形式(如
a++):先参与表达式运算,再自增。
- 前置形式(如
4. 正负号 + 和 -
- 功能:表示操作数的正负性(正号可省略,负号用于取负数)。
5. 计算大小 sizeof
- 功能:计算操作数(变量或类型)在内存中占用的字节数。
- 注意:
sizeof是操作符而非函数,括号在变量名时可省略(如sizeof a),类型名必须保留(如sizeof(int))。
6. 取地址 & 和指针解引用 *
- 取地址
&:获取变量的内存地址(用于指针操作)。 - 解引用
*:通过指针地址获取对应内存中的值(需配合指针变量使用)。
7.(类型) 强制类型转换
6.2 示例代码1
#include <stdio.h>
int main() {
int a = 5;
int b = 0;
int c = 0x1234; // 十六进制数(二进制:0001 0010 0011 0100)
// 1. 逻辑非 !
printf("逻辑非演示:\n");
printf("!5 = %d(5是非0值,逻辑真,取反后为假)\n", !a); // 输出0
printf("!0 = %d(0是假,取反后为真)\n\n", !b); // 输出1
// 2. 按位取反 ~
printf("按位取反演示(假设为16位整数):\n");
printf("~0x1234 = 0x%x(二进制每一位取反)\n\n", ~c); // 输出0xedcb(二进制:1110 1101 1100 1011)
// 3. 自增 ++(前置 vs 后置)
int x = 10;
int y = x++; // 后置:先赋值y=x(10),再x自增为11
int z = ++x; // 前置:先x自增为12,再赋值z=x(12)
printf("自增演示:\n");
printf("x=%d, y=%d, z=%d\n\n", x, y, z); // 输出x=12, y=10, z=12
// 4. 正负号 + 和 -
int num = 8;
printf("正负号演示:\n");
printf("-num = %d(取负数)\n", -num); // 输出-8
printf("+num = %d(正号可省略)\n\n", +num); // 输出8
// 5. 计算大小 sizeof
printf("sizeof演示:\n");
printf("sizeof(int) = %zu字节\n", sizeof(int)); // 输出4(常见32/64位系统)
printf("sizeof(a) = %zu字节(变量名可省略括号)\n\n", sizeof a); // 输出4
// 6. 取地址 & 和指针解引用 *
int var = 100;
int* p = &var; // 取var的地址存入指针p
printf("指针操作演示:\n");
printf("var的地址:%p\n", &var); // 输出var的内存地址(如0x7ffd...)
printf("*p = %d(通过指针解引用获取值)\n", *p); // 输出100
return 0;
}
6.3 关键注意事项
- 自增 / 自减操作符的前置和后置形式在表达式中会影响结果,需根据场景选择。
sizeof对数组名计算时返回整个数组的大小(如int arr[5],sizeof(arr)为 20 字节),但数组名作为参数传入函数后会退化为指针,此时sizeof结果为指针大小(4 或 8 字节)。- 按位取反
~的结果与系统的整数位数(如 16 位、32 位)相关,示例中假设为 16 位整数,实际结果可能因环境不同而变化。 - 指针解引用
*需确保指针指向有效内存,否则会导致未定义行为(如空指针解引用)。
七、关系操作符
定义:用于比较两个表达式并返回布尔值(真 / 假)的运算符,结果用整数1(真)和0(假)表示。
7.1 常用关系操作符
| 操作符 | 描述 | 示例 | 结果 |
|---|---|---|---|
> | 大于 | 5 > 3 | 1 |
< | 小于 | 5 < 3 | 0 |
>= | 大于等于 | 5 >= 5 | 1 |
<= | 小于等于 | 3 <= 5 | 1 |
== | 等于(值相等) | 5 == 5 | 1 |
!= | 不等于 | 5 != 3 | 1 |
使用注意事项
- 避免混淆赋值与比较
- 错误:
if (x = 5)(赋值操作,始终为真) - 正确:
if (x == 5)(比较操作)
- 错误:
- 数据类型影响结果c运行
float a = 0.1 + 0.2; printf("%d", a == 0.3); // 可能输出0(浮点数精度问题) - 优先级规则
- 关系运算符优先级低于算术运算符,但高于赋值运算符。
示例:a + b > c - d等价于(a + b) > (c - d)
- 关系运算符优先级低于算术运算符,但高于赋值运算符。
典型应用场景
- 条件判断c运行
if (age >= 18) { printf("成年人\n"); } - 循环控制c运行
while (i < 10) { i++; } - 多条件组合c运行
if (score >= 90 && score <= 100) { printf("优秀\n"); }
常见错误案例
- 错误比较字符串c运行
char str1[] = "hello"; char str2[] = "hello"; if (str1 == str2) { ... } // 错误!比较的是地址而非内容 // 正确:使用strcmp函数 - 浮点精度问题c运行
double x = 1.0 / 3.0; if (x * 3 == 1.0) { ... } // 可能失败 // 正确:使用容差比较 if (fabs(x * 3 - 1.0) < 1e-9) { ... }
7.2优先级与结合性
| 类别 | 操作符 | 结合性 |
|---|---|---|
| 算术运算符 | + - * / | 左到右 |
| 关系运算符 | > < >= <= | 左到右 |
| 相等运算符 | == != | 左到右 |
| 赋值运算符 | = += -= *= /= | 右到左 |
总结:关系操作符是 C 语言中控制程序逻辑的基础工具,需注意数据类型、优先级和边界条件,避免常见陷阱。
八、逻辑操作符
在 C 语言里,逻辑操作符主要用于对表达式进行逻辑运算,运算结果为布尔值,也就是true(在 C 语言中用非零值表示)或者false(在 C 语言中用 0 表示)。下面为你详细介绍 C 语言中的逻辑操作符。
8.1 逻辑与(&&)
- 功能:当且仅当两个操作数都为真时,结果才为真。只要有一个操作数为假,结果就为假。
- 使用格式:
expression1 && expression2 - 运算规则:先对
expression1进行求值,如果它的值为假,就不会再对expression2求值了,因为此时整个表达式的结果必然为假;只有当expression1的值为真时,才会继续对expression2进行求值。
示例代码:
#include <stdio.h>
int main() {
int a = 5, b = 10, c = 0;
// 两个操作数都为真,结果为真(1)
printf("%d\n", (a > 0) && (b > 0)); // 输出:1
// 其中一个操作数为假,结果为假(0)
printf("%d\n", (a > 0) && (c > 0)); // 输出:0
// 短路特性:由于a < 0为假,不会执行printf
(a < 0) && printf("This won't print\n"); // 无输出
return 0;
}8.2 逻辑或(||)
- 功能:只要两个操作数中有一个为真,结果就为真;只有当两个操作数都为假时,结果才为假。
- 使用格式:
expression1 || expression2 - 运算规则:先对
expression1进行求值,如果它的值为真,就不会再对expression2求值了,因为此时整个表达式的结果必然为真;只有当expression1的值为假时,才会继续对expression2进行求值。
示例代码:
#include <stdio.h>
int main() {
int a = 5, b = 10, c = 0;
// 两个操作数都为真,结果为真(1)
printf("%d\n", (a > 0) || (b > 0)); // 输出:1
// 其中一个操作数为真,结果为真(1)
printf("%d\n", (a > 0) || (c > 0)); // 输出:1
// 短路特性:由于a > 0为真,不会执行printf
(a > 0) || printf("This won't print\n"); // 无输出
return 0;
}8.3 逻辑非(!)
- 功能:对操作数的逻辑状态取反,也就是操作数为真时结果为假,操作数为假时结果为真。
- 使用格式:
!expression - 运算规则:若
expression的值为真(非零),则!expression的值为假(0);若expression的值为假(0),则!expression的值为真(1)。
示例代码:
#include <stdio.h>
int main() {
int a = 5, c = 0;
// 操作数为真,取反后为假(0)
printf("%d\n", !(a > 0)); // 输出:0
// 操作数为假,取反后为真(1)
printf("%d\n", !(c > 0)); // 输出:1
return 0;
}8.4 注意要点
- 优先级问题:逻辑非(
!)的优先级高于算术操作符,而逻辑与(&&)和逻辑或(||)的优先级低于关系操作符。在实际使用时,要注意合理添加括号来明确运算顺序。c运行// 等价于 (a > 0) && (b > 0) a > 0 && b > 0 // 等价于 (!a) || (b > 0) !a || b > 0
// 等价于 (a > 0) && (b > 0)
a > 0 && b > 0
// 等价于 (!a) || (b > 0)
!a || b > 0- 短路求值特性:逻辑与和逻辑或操作符都具有短路求值的特性,利用这一特性可以避免一些潜在的错误。c运行
// 当ptr为NULL时,由于短路特性,不会执行*(ptr) if (ptr != NULL && *ptr > 0) { // 执行相应操作 }
// 当ptr为NULL时,由于短路特性,不会执行*(ptr)
if (ptr != NULL && *ptr > 0) {
// 执行相应操作
}- 与按位操作符的差异:逻辑操作符(
&&、||、!)进行的是逻辑运算,运算结果为布尔值;而按位操作符(&、|、~)进行的是逐位运算,运算结果是整数。c运行// 逻辑与 printf("%d\n", 5 && 0); // 输出:0 // 按位与 printf("%d\n", 5 & 0); // 输出:0(5的二进制是101,0的二进制是000,按位与结果为000)
// 逻辑与
printf("%d\n", 5 && 0); // 输出:0
// 按位与
printf("%d\n", 5 & 0); // 输出:0(5的二进制是101,0的二进制是000,按位与结果为000)- 常见应用场景:逻辑操作符常用于条件语句(如
if、while)和循环控制中。c运行// 判断一个数是否在1到100之间 if (num >= 1 && num <= 100) { printf("Valid\n"); } // 判断一个字符是否为数字或字母 if ((ch >= '0' && ch <= '9') || (ch >= 'A' && ch <= 'Z')) { printf("Alphanumeric\n"); }
// 判断一个数是否在1到100之间
if (num >= 1 && num <= 100) {
printf("Valid\n");
}
// 判断一个字符是否为数字或字母
if ((ch >= '0' && ch <= '9') || (ch >= 'A' && ch <= 'Z')) {
printf("Alphanumeric\n");
}8.5 求闰年
is_leap_year(int y)
{
if (((y % 4 == 0) && (y % 100 != 0)) || (y % 400 == 0))
{
return 1;
}
else
{
return 0;
}
}8.6 优先级案例1(复习)
int main()
{
int i = 0, a = 0, b = 2, c = 3, d = 4;
i = a++ && ++b && d++;
printf("a=%d\nb=%d\ni=%d\nd=%d\n", a, b, i, d);
return 0;
}结果:
a=1
b=2
i=0
d=4关键点:
- 逻辑与(
&&)的短路特性:当左侧操作数为假(0)时,右侧操作数不会执行。 - 后缀自增(
a++):先返回原值,再自增。 - 前缀自增(
++b):先自增,再返回新值。
执行过程:
a++返回 0(假),随后a变为 1- 由于左侧为假,
++b和d++被短路(不执行) - 整个表达式结果为 0,赋值给
i - 最终
b和d保持原值不变
8.6 优先级案例2(复习)
int main()
{
int i = 0, a = 1, b = 2, c = 3, d = 4;
i = a++ && ++b && d++;
printf("a=%d\nb=%d\ni=%d\nd=%d\n", a, b, i, d);
return 0;
}结果:
a=2
b=3
i=1
d=5关键点:
- 逻辑与(
&&)的短路特性:只有当左侧操作数为真(非 0)时,才会继续计算右侧。 - 后缀自增(
a++、d++):先返回原值,再自增。 - 前缀自增(
++b):先自增,再返回新值。
执行过程:
- 计算
a++:返回a的原值 1(真),随后a变为 2 - 计算
++b:b先自增为 3,返回 3(真) - 计算
d++:返回d的原值 4(真),随后d变为 5 - 整个表达式为真:结果为 1,赋值给
i
最终变量值:
a=2(执行了a++)b=3(执行了++b)i=1(逻辑表达式结果为真)d=5(执行了d++)
8.7 优先级案例3(复习)
int main()
{
int i = 0, a = 0, b = 2, c = 3, d = 4;
//i = a++ && ++b && d++;
i = a++ || ++b || d++;
printf("a=%d\nb=%d\ni=%d\nd=%d\n", a, b, i, d);
return 0;
// a = 1; b = 3; d = 4; i = 1;
}关键点:
- 逻辑或(
||)的短路特性:只要左侧操作数为真(非 0),就会立即终止计算,右侧操作数不会执行。 - 后缀自增(
a++):先返回原值,再自增。 - 前缀自增(
++b):先自增,再返回新值。
执行过程:
- 计算
a++:返回a的原值 0(假),随后a自增为 1。 - 计算
++b:- 由于
a++返回假,继续计算右侧的++b。 b先自增为 3,再返回 3(真)。
- 由于
- 短路发生:
- 由于
++b返回真,逻辑或表达式已确定为真,d++不会执行,因此d保持原值 4。
- 由于
- 结果赋值:整个表达式结果为 1(真),赋值给
i。
最终变量值:
a=1(a++执行后自增)b=3(++b执行后自增)i=1(逻辑或表达式结果为真)d=4(d++因短路未执行)
8.8 总结
&& 左边为假,右边就不计算了
|| 左边为真,右边就不计算了
九、条件操作符(三目操作符)
在 C 语言里,条件操作符(? :)是一种能替代简单if-else语句的便捷工具。其基本形式为:条件 ? 值1 : 值2。
工作原理:
- 当条件为真(非 0)时,返回值 1。
- 当条件为假(0)时,返回值 2。
示例:
int a = 5, b = 10;
int max = (a > b) ? a : b; // 因为a > b不成立,所以max的值为b,即10
主要用途:
- 简化赋值操作
int abs_value = (num < 0) ? -num : num; // 获取绝对值
- 避免除以零的错误
float result = (divisor != 0) ? (10.0 / divisor) : 0;
注意事项:
- 要留意运算符的优先级,建议使用括号来明确运算顺序。
- 表达式的结果类型要保持兼容。
十、逗号表达式
在 C 语言中,逗号表达式是一种使用逗号运算符,将多个表达式连接起来的特殊表达式。逗号表达式会从左到右依次计算每个子表达式,并返回最后一个子表达式的值。
10.1 基本语法和特性
表达式1, 表达式2, 表达式3, ..., 表达式N
- 计算顺序:严格从左到右依次计算每个子表达式。
- 返回值:整个逗号表达式的值是最后一个子表达式(表达式 N)的值。
- 优先级:逗号运算符的优先级是所有运算符中最低的,因此通常需要用括号明确运算顺序。
10.2 示例分析
- 简单的逗号表达式
int a = (3 + 5, 7 * 2, 10 - 4); // a的值为6(最后一个表达式10-4的结果)计算过程:
- 先计算
3 + 5,结果为 8(被丢弃)。 - 再计算
7 * 2,结果为 14(被丢弃)。 - 最后计算
10 - 4,结果为 6,作为整个表达式的值赋给a。
- 结合赋值操作
int x, y, z;
x = (y = 3, y + 2); // 先将3赋给y,然后计算y+2,x的值为5
- 在 for 循环中使用
for (int i = 0, j = 10; i < j; i++, j--) {
printf("i=%d, j=%d\n", i, j);
}
- 初始化部分
int i = 0, j = 10使用逗号分隔多个变量声明。 - 迭代部分
i++, j--使用逗号表达式同时更新两个变量。
10.3 实际应用场景
- 多变量初始化或更新
int a, b, c;
(a = 1, b = 2, c = a + b); // 同时初始化多个变量
- 函数调用中的参数列表
void func(int x, int y);
func((a++, b++), (c = a + b)); // 逗号表达式作为参数传递
- 宏定义中的复杂操作
#define SWAP(a, b) ((a)=(a)+(b), (b)=(a)-(b), (a)=(a)-(b))
10.4 注意事项
- 避免混淆逗号的不同用途
- 函数参数分隔符:
func(a, b)中的逗号不是逗号运算符。 - 变量声明分隔符:
int a, b;中的逗号也不是逗号运算符。
- 函数参数分隔符:
- 慎用复杂的逗号表达式
虽然逗号表达式可以让代码更简洁,但过度使用会降低代码的可读性。例如:
result = (a = 1, b = 2, c = a + b, d = c * 2); // 可读性较差
- 运算顺序的严格性
逗号表达式确保子表达式按顺序计算,这在需要副作用(如修改变量)的场景中很重要:
int i = 0;
int x = (i++, i++); // x的值为1(先i变为1,再i变为2,最后返回第二个i++的值1)与其他语言的对比
- C/C++:逗号表达式是语言的一部分,有明确的运算规则。
- Python/Java:没有直接等价的逗号表达式,但可以通过序列操作或方法链实现类似效果。
合理使用逗号表达式可以让代码更简洁,但应避免在可读性上妥协。
十一、下标引用、函数调用和结构成员
11.1 下标引用(数组访问)
比特案例
int main()
{
int arr[10] = { 0 };
// arr[7] --> *(arr+7) --> *(7+arr) --> 7[arr];
// *(arr + 7) 就是第八个元素
arr[7] = 8;
7[arr] = 9;
return 0;
}
// arr[7] –> *(arr+7) –> *(7+arr) –> 7[arr];
// *(arr + 7) 就是第八个元素
借助下标引用操作符[],你可以对数组元素进行访问。
int arr[5] = {10, 20, 30, 40, 50};
int third = arr[2]; // 获取数组的第3个元素,结果为30
arr[4] = 500; // 修改数组的第5个元素
要点提示:
- 数组下标是从 0 开始的,有效范围是
0到长度-1。 - 若访问的下标超出数组范围,会引发未定义行为。
- 多维数组的访问方式为
arr[i][j],例如:
int matrix[2][3] = {{1,2,3}, {4,5,6}};
int value = matrix[1][2]; // 结果为611.2 函数调用
通过函数调用操作符(),你可以执行函数并传递参数。
int add(int a, int b) {
return a + b;
}
int result = add(3, 5); // 调用add函数,结果为8核心细节:
- 函数参数可以是常量、变量或者表达式。
- 参数传递方式有值传递和指针传递两种:
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
swap(&x, &y); // 通过指针传递来交换x和y的值
- 函数也可以没有参数或者返回值:
void print_hello() {
printf("Hello\n");
}
- sizeof int,不需要函数调用操作符也可以运行,所以sizeof不是函数
11.3 结构成员访问
比特案例
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct Stu {
char name[10];
int age;
char sex[5];
double score;
};
void set_age1(struct Stu ss)
{
strcpy(ss.name, "zhangsan");
ss.age = 20;
ss.score = 100.0;
}
void print_stu(struct Stu ss)
{
printf("%s %d %lf\n", ss.name, ss.age, ss.score);
}
int main()
{
struct Stu s = { 0 };
set_stu(s);
printf_stu(s);
return 0;
}原因分析:
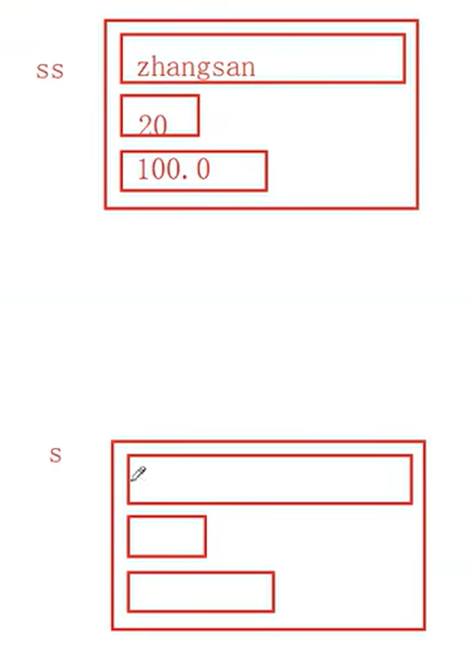
更改:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct Stu {
char name[10];
int age;
char sex[5];
double score;
};
void set_stu(struct Stu ss)
{
strcpy(ss.name, "zhangsan");
ss.age = 20;
ss.score = 100.0;
}
void set_stu1(struct Stu* ps)
{
/*strcpy((*ps).name, "zhangsan");
(*ps).age = 20;
(*ps).score = 100.0;*/
strcpy(ps->name, "张三");
ps->age = 20;
ps->score = 100;
}
void print_stu(struct Stu ss)
{
printf("%s %d %lf\n", ss.name, ss.age, ss.score);
}
int main()
{
struct Stu s = { 0 };
//set_stu(s);
set_stu1(&s);
print_stu(s);
return 0;
}结构体指针 -> 成员,ps->age 完全等价于 (*ps).age 先找到对象,再找到成员
结构体对象.成员
结构成员访问操作符有.(用于结构体变量)和->(用于结构体指针)。
struct Point {
int x;
int y;
};
struct Point p1 = {10, 20};
struct Point* ptr = &p1;
int a = p1.x; // 使用.访问成员,结果为10
int b = ptr->y; // 使用->通过指针访问成员,结果为20
使用技巧:
ptr->member其实等价于(*ptr).member。- 结构体可以进行嵌套,访问嵌套成员的方式为:
struct Rectangle {
struct Point top_left;
struct Point bottom_right;
};
struct Rectangle rect;
int x = rect.top_left.x; // 访问嵌套结构体的成员
11.4 三者的综合运用
下面通过一个示例来展示这三种操作的综合使用:
struct Student {
char name[50];
int scores[3];
};
// 计算学生的平均分数
float calculate_average(struct Student* s) {
int sum = 0;
for (int i = 0; i < 3; i++) {
sum += s->scores[i]; // 结合->和[]操作
}
return (float)sum / 3;
}
// 主函数
int main() {
struct Student s = {"Alice", {85, 90, 95}};
float avg = calculate_average(&s); // 调用函数
printf("Average: %.2f\n", avg); // 输出:Average: 90.00
return 0;
}11.5 关键注意事项
- 下标越界问题:在访问数组时,一定要确保下标在有效范围之内。
- 函数参数匹配:调用函数时,传递的参数类型和数量要与函数定义一致。
- 指针有效性检查:在使用
->操作符前,要确保指针不是NULL。 - 结构体初始化:可以使用初始化列表对结构体成员进行初始化,如
struct Point p = {.x=1, .y=2};。
十二、表达式求值
表达式求值的顺序一部分是由操作符的优先级和结合性决定
同样,有些表达式的操作数在求值的过程中可能需要转换为其他类型。
#include <stdio.h>
int main()
{
int a = 2 + 6 / 3; // 优先级
int b = 2 + 2 + 2 + 3; // 结合性,优先级相同的情况下
return 0;
}12.1 隐式类型转换
C的整型算术运算总是至少以缺省整型类型的精度来进行的。
为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
整型提升的意义:CPU通常以int大小的数据进行运算效率最高
表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行运算。
char a = 25;
char b = 124;
char c = a + b;- a和c的值被提升为普通整型,然后再进行加法运算。
- 加法运算完成之后,结果将被截断,然后存储在a中
如何进行整型整体提升呢?
整形提升是按照变量的数据类型的符号位来提升的
以下是整型提升的三种案例
1、负数的整型提升
char c1 = -1;

char c = -1;// -1是整数,32个比特位
// 10000000000000000000000000000001 原码
// 11111111111111111111111111111110 反码
// 11111111111111111111111111111111 补码 -1的补码
// 截断:11111111 -c 整形提升是按照变量的数据类型的符号位来提升的
// 整型提升
// 111111111111111111111111111111112、正数的整型提升,高位补充符号位,即为0
char c2 = 1;

3、无符号整型提升,高位补0;
12.2 整型提升的例子(鹏哥案例,重点)
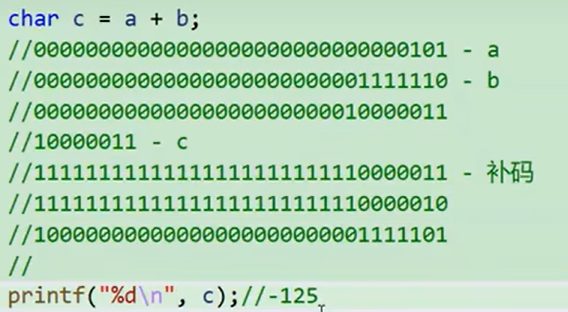
char a = 5;
char b = 126;
// 0
char c = a + b;
printf("%d\n", c); // -125这展示了 C 语言中整数溢出的典型行为,结果会 “环绕” 到数据类型的取值范围另一端。若要避免溢出问题,可使用更大的数据类型(如int)来存储结果。
正数的原反补都是一样
内存中都是以补码形式存在的(整型家族
signed char,short,int,long,long long在内存中均是以补码存在的)ASCII的取值范围是0-127的
这是因为补码有很多优势:统一的加减运算、唯一的零表示、硬件实现简单
详细解释
使用补码的数据类型
有符号整数类型确实普遍使用补码表示,包括:
signed char,short,int,long,long long- 这是因为补码有很多优势:统一的加减运算、唯一的零表示、硬件实现简单
不使用补码的数据类型
无符号整数类型:
unsigned char,unsigned short,unsigned int等- 使用纯二进制表示,没有符号位概念
浮点数类型:
float,double,long double- 使用IEEE 754标准,采用符号位+指数+尾数的格式,与补码完全不同
指针类型:
- 通常作为无符号整数处理,直接存储内存地址
字符类型:
char的符号性由实现定义,可能是有符号(补码)或无符号特殊情况
某些嵌入式系统或特殊硬件可能使用其他表示方法(如反码),但现代主流系统几乎都对有符号整数使用补码。
所以更准确的说法是:有符号整数类型在现代系统中普遍使用补码,但这并不适用于所有数据类型。
这个问题涉及C语言中字符类型的算术运算和整数溢出。让我用二进制的角度来详细解释:
变量的二进制表示
char a = 5:
- 5的二进制:
00000101
char b = 126:
- 126的二进制:
01111110
加法运算过程
当执行 char c = a + b 时:
00000101 (5)
+ 01111110 (126)
-----------
10000011 (131的二进制)
关键问题:char的取值范围
在大多数系统中,char 是有符号8位整数:
- 取值范围:-128 到 127
- 最高位是符号位(0表示正数,1表示负数)
溢出分析
计算结果是131,但这超出了有符号char的范围(127),发生了整数溢出。
131的二进制是 10000011,在有符号char中:
- 最高位是1,表示这是负数
- 需要用二补数来解释这个负数
二补数计算
对于 10000011:
- 按位取反:
01111100 - 加1:
01111101= 125 - 加上负号:-125
结果验证
所以 c 的值是 -125,这就是为什么 printf("%d\n", c) 输出 -125。
总结
这是典型的有符号整数溢出行为:当结果超出数据类型能表示的最大值时,会”环绕”到负数范围。在二进制层面,就是最高位变成了1,被解释为符号位,导致结果变成了负数。
12.3 整型提升的例子2
char a = 0xb6; // 这里是补码
short b = 0xb600;
int c = 0xb6000000;
if (a == 0xb6)
{
printf("a");
}
if (b == 0xb600)
{
printf("b");
}
if (c == 0xb6000000)
{
printf("c");
}从整型提升的角度来分析这段代码:
整型提升规则
在C语言中,当char和short类型参与运算或比较时,会自动提升为int类型。这是因为CPU通常以int大小的数据进行运算效率最高。
逐行分析
变量声明部分
char a = 0xb6; // a = -74 (signed char)
short b = 0xb600; // b = -18944 (signed short)
int c = 0xb6000000; // c = -1241513984 (signed int)
关键点:char和short默认是有符号类型,最高位为符号位。
比较操作中的整型提升
第一个if语句:
if (a == 0xb6) // a会提升为int进行比较
a(char类型,值为-74)提升为int类型,变成0xFFFFFFB6(-74的32位表示)0xb6是int字面量,值为182- 比较:
0xFFFFFFB6 != 0x000000B6,条件为假,不输出”a”
第二个if语句:
if (b == 0xb600) // b会提升为int进行比较
b(short类型,值为-18944)提升为int类型,变成0xFFFFB6000xb600是int字面量,值为46592- 比较:
0xFFFFB600 != 0x0000B600,条件为假,不输出”b”
第三个if语句:
if (c == 0xb6000000) // 都是int类型,无需提升
c本身就是int类型,无需提升- 两个值都是
0xb6000000,比较结果为真,输出”c”
程序输出结果
程序只会输出:c
核心概念
整型提升的本质是符号扩展:
- 正数:高位补0
- 负数:高位补1(保持二进制补码表示的一致性)
这就是为什么负数的char和short在提升为int后,与原来的十六进制字面量不相等的原因。
二进制的转换过程1
第一步:十六进制转二进制
0xb6 = 10110110 (二进制)第二步:理解signed char的存储
signed char是8位有符号整数- 取值范围:-128 到 +127
- 使用二进制补码表示负数
第三步:判断正负数
10110110 ^ 最高位是1,说明这是负数第四步:计算负数的值
对于二进制补码,负数的计算方法:
- 按位取反:
10110110→01001001- 加1:
01001001+1=01001010- 转为十进制:
01001010= 64 + 8 + 2 = 74- 加负号:-74
验证计算
我们可以反向验证:
- -74的二进制补码表示:
- 74的二进制:
01001010- 按位取反:
10110101- 加1:
10110110- 结果正好是
0xb6!关键概念
二进制补码是计算机存储有符号整数的标准方法:
- 正数:直接用二进制表示
- 负数:正数的二进制按位取反后加1
所以
0xb6作为8位有符号数就是 -74。让我详细解释
short b = 0xb600如何得到 -18944 这个值:二进制转换过程2
第一步:十六进制转二进制
0xb600 = 1011 0110 0000 0000 (二进制,16位)第二步:理解signed short的存储
signed short是16位有符号整数- 取值范围:-32768 到 +32767
- 使用二进制补码表示负数
第三步:判断正负数
1011 0110 0000 0000 ^ 最高位是1,说明这是负数第四步:计算负数的值(二进制补码方法)
对于二进制补码,负数的计算:
- 按位取反:
1011 0110 0000 0000→0100 1001 1111 1111- 加1:
0100 1001 1111 1111+1=0100 1010 0000 0000- 转为十进制:
0100 1010 0000 0000 = 16384 + 2048 + 512 = 18944- 加负号:-18944
验证计算
反向验证 -18944 的二进制补码:
- 18944的二进制:
0100 1010 0000 0000- 按位取反:
1011 0101 1111 1111- 加1:
1011 0110 0000 0000- 转为十六进制:
0xb600✓另一种理解方法
也可以直接用权重计算:
1011 0110 0000 0000 (作为16位有符号数) = -32768×1 + 16384×0 + 8192×1 + 4096×1 + 2048×0 + 1024×1 + 512×1 + 256×0 + ... + 1×0 = -32768 + 8192 + 4096 + 1024 + 512 = -32768 + 13824 = -18944所以
0xb600作为16位有符号数就是 -18944。
12.4 整型提升的例子3
char c = 1;
printf("%u\n", sizeof(c));
printf("%u\n", sizeof(+c));
printf("%u\n", sizeof(-c));
//输出
1
4
4示例中,c只要参与了表达式的运算,就会发生整型提升,表达式+c就会发生提升,所以sizeof(+c)是4个字节
1. sizeof(+c) – 输出 4
- 关键点:一元运算符
+触发了整型提升 - 提升过程:
c是char类型(1字节)- 应用一元
+运算符时,char被提升为int +c的类型变成int(通常4字节)sizeof(+c)计算的是int的大小
2. sizeof(-c) – 输出 4
- 同样,一元运算符
-也触发整型提升 - 提升过程与
+c相同:c从char提升为int- 然后对
int值取负 - 结果仍是
int类型
C语言的整型提升规则规定:
- 当
char、short、位域或相应的unsigned类型参与运算时 - 如果
int能表示原类型的所有值,则提升为int - 否则提升为
unsigned int
触发整型提升的情况
- 算术运算符:
+、-、*、/、% - 比较运算符:
<、>、==等 - 位运算符:
&、|、^、<<、>> - 一元运算符:
+、-、~ - 函数调用:可变参数函数的参数
12.5 算术转换
如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数的转换为另一个操作数的类型,否则操作就无法进行。下面的层次体系称为寻常算术转换。

- 如果某个操作数的类型在上面这个列表中排名较低,那么首先要转换为另外一个操作数的类型后执行运算
警告
但是算术转换要合理,要不然会有一些潜在的问题。
float f= 3.14;
int num =f;//隐式转换,会有精度丢失十三、操作符属性
13.1 复杂表达式的求值有三个影响的因素
1.操作符的优先级
2.操作符的结合性
3.是否控制求值顺序.
两个相邻的操作符先执行哪个?取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。操作符优先级
13.2 操作符汇总表
汇总表
| 操作符 | 描述 | 用法示例 | 结果类型 | 结合性 | 是否控制流操作 | 备注 |
|---|---|---|---|---|---|---|
| () | 分组 | (表达式) | 与表达式相同 | N/A | 否 | |
| () | 函数调用 | rexp (rexp, …rexp) | rexp | L-R | 否 | |
| [] | 下标引用 | rexp[rexp] | lexp | L-R | 否 | |
| . | 访问成员或成员 | lexp.member_name | lexp | L-R | 否 | |
| -> | 访问成员或成员名 | rexp->member_name | lexp | L-R | 否 | |
| ++ | 后缀自增 | lexp ++ | rexp | L-R | 否 | |
| — | 后缀自减 | lexp — | rexp | L-R | 否 | |
| ! | 逻辑反 | ! rexp | rexp | R-L | 否 | |
| – | 按位取反 | – rexp | rexp | R-L | 否 | |
| + | 单目、条件运算 | + rexp | rexp | R-L | 否 | |
| – | 单目、条件加减 | + rexp | rexp | R-L | 否 | |
| ++ | 前缀自增 | ++ lexp | rexp | R-L | 否 | |
| — | 前缀自减 | — lexp | rexp | R-L | 否 | |
| * | 间接引用 | * rexp | lexp | R-L | 否 | |
| & | 取地址 | & lexp | rexp | R-L | 否 | |
| sizeof | 取数长度、以字节为单位 | sizeof rexp sizeof(类型) | rexp | R-L | 否 | |
| (类型) | 类型转换 | (类型) rexp | rexp | R-L | 否 | |
| * | 乘法 | rexp * rexp | rexp | L-R | 否 | |
| / | 除法 | rexp / rexp | rexp | L-R | 否 | |
| % | 整数取余 | rexp % rexp | rexp | L-R | 否 | |
| + | 加法 | rexp + rexp | rexp | L-R | 否 | |
| – | 减法 | rexp – rexp | rexp | L-R | 否 | |
| << | 左移位 | rexp << rexp | rexp | L-R | 否 | |
| >> | 右移位 | rexp >> rexp | rexp | L-R | 否 | |
| < | 小于 | rexp < rexp | rexp | L-R | 否 | |
| <= | 小于等于 | rexp <= rexp | rexp | L-R | 否 | |
| > | 大于 | rexp > rexp | rexp | L-R | 否 | |
| >= | 大于等于 | rexp >= rexp | rexp | L-R | 否 | |
| == | 等于 | rexp == rexp | rexp | L-R | 否 | |
| != | 不等于 | rexp != rexp | rexp | L-R | 否 | |
| & | 位与 | rexp & rexp | rexp | L-R | 否 | |
| ^ | 位异或 | rexp ^ rexp | rexp | L-R | 否 | |
| | | 位或 | rexp | rexp | rexp | L-R | 否 | |
| && | 逻辑与 | rexp && rexp | rexp | L-R | 是 | |
| || | 逻辑或 | rexp || rexp | rexp | L-R | 是 | |
| ? : | 条件操作符 | rexp ? rexp : rexp | rexp | N/A | 是 | |
| = | 赋值 | lexp = rexp | rexp | R-L | 否 | |
| += | 以…加 | lexp += rexp | rexp | R-L | 否 | |
| -= | 以…减 | lexp -= rexp | rexp | R-L | 否 | |
| *= | 以…乘 | lexp *= rexp | rexp | R-L | 否 | |
| /= | 以…除 | lexp /= rexp | rexp | R-L | 否 | |
| %= | 以…取模 | lexp %= rexp | rexp | R-L | 否 | |
| <<= | 以…左移 | lexp <<= rexp | rexp | R-L | 否 | |
| >>= | 以…右移 | lexp >>= rexp | rexp | R-L | 否 | |
| &= | 以…与 | lexp &= rexp | rexp | R-L | 否 | |
| ^= | 以…异或 | lexp ^= rexp | rexp | R-L | 否 | |
| |= | 以…或 | lexp |= rexp | rexp | R-L | 否 | |
| , | 逗号 | rexp, rexp | rexp | L-R | 是 |
说明
- rexp: 右值表达式 (right-value expression)
- lexp: 左值表达式 (left-value expression)
- L-R: 左结合 (Left-to-Right associativity)
- R-L: 右结合 (Right-to-Left associativity)
- N/A: 不适用
- 是否控制流操作: 指该操作符是否会影响程序执行流程
优先级顺序
表格中的操作符按照优先级从高到低排列,同一行的操作符具有相同的优先级。
13.3 一些问题表达式
非法代码1
//表达式的求值部分由操作符的优先级决定,
//表达式1
a*b + c*d + e*f
虽然答案都正确,没有唯一确定的答案、
非法代码2

注释:同上,操作符的优先级只能决定自减-的运算在+的运算的前面,但是我们并没有办法得知,+操作符的左操作数的获取在右操作数之前还是之后求值,所以结果是不可预测的,是有歧义的。
非法代码3
非法代码4

这个代码有没有实际的问题?
有问题!
虽然在大多数的编译器上求得结果都是相同的。
但是上述代码 answer = fun()-fun()*fun();
我们只能通过操作符的优先级得知:先算乘法再算减法。
函数的调用先后顺序无法通过操作符的优先级确定。
非法代码5
int a = 1;
int b = (++a) + (++a) + (++a);
printf("%d\n", b);VS运行结果12,linux运行结果10
这个C代码的结果是未定义行为,不同的编译器和编译选项可能产生不同的结果。
问题在于这一行:
cint b = (++a) + (++a) + (++a);这里存在**序列点(sequence point)**问题。在同一个表达式中多次修改同一个变量
a,而在相邻的序列点之间,变量的修改顺序是未定义的。可能的执行顺序包括:
- 从左到右:a变为2,然后3,然后4,结果b = 2+3+4 = 9
- 从右到左:a变为2,然后3,然后4,结果b = 4+3+2 = 9
- 其他顺序:可能得到不同的结果
实际测试中,很多编译器会输出
12,这是因为编译器可能会:
- 先计算所有的
++a操作,使a变为4- 然后计算 4+4+4 = 12
但这个行为不可移植,在不同编译器、不同优化级别下可能得到不同结果。正确的做法是将操作分开
cint a = 1;
++a; // a = 2
++a; // a = 3
++a; // a = 4
int b = a + a + a; // b = 12
总结:我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径,那这个表达式就是存在问题
的。
本文转载自,原文链接:https://blog.csdn.net/ljh86/article/details/130537197,本文观点不代表何大锤的博客立场。




