一、进制转换详解
1. 二进制(Binary)↔ 十六进制(Hexadecimal)
核心逻辑:利用十六进制与二进制的天然对应关系(1 位十六进制 = 4 位二进制)。
二进制转十六进制
- 步骤:
- 从右往左将二进制数每 4 位 分组,不足 4 位时在左侧补
0。 - 每组转换为对应的十六进制数(
0-9对应0-9,10-15对应A-F)。
- 从右往左将二进制数每 4 位 分组,不足 4 位时在左侧补
- 示例:
- 二进制
10110101→ 分组为10110101→ 十六进制B5。 - 二进制
00001111→ 分组为00001111→ 十六进制0F。
- 二进制
十六进制转二进制
- 步骤:
- 每位十六进制数转换为对应的 4 位二进制数(不足 4 位补前导
0)。 - 合并所有二进制组。
- 每位十六进制数转换为对应的 4 位二进制数(不足 4 位补前导
- 示例:
- 十六进制
3A→3→0011,A→1010→ 二进制00111010。 - 十六进制
FF→F→1111,F→1111→ 二进制11111111。
- 十六进制
2. 二进制(Binary)↔ 十进制(Decimal)
核心逻辑:二进制按权展开,十进制通过除法取余。
二进制转十进制
- 步骤: 从右往左,每位二进制数乘以
2^n(n为从 0 开始的位数索引),求和。 - 公式:
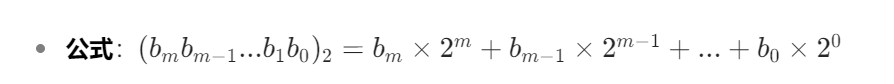
- 示例:
- 二进制
1011→1×2^3 + 0×2^2 + 1×2^1 + 1×2^0 = 8+0+2+1=11。
- 二进制
十进制转二进制
- 步骤:
- 用十进制数除以
2,记录余数(必为0或1)。 - 重复除以
2,直到商为0。 - 余数逆序排列即为二进制数。
- 用十进制数除以
- 示例:
- 十进制
23→ 除以 2 的余数序列:1, 1, 1, 0, 1(逆序后为10111)。
- 十进制
3. 二进制(Binary)↔ 八进制(Octal)
核心逻辑:八进制与二进制的对应关系(1 位八进制 = 3 位二进制)。
二进制转八进制
- 步骤:
- 从右往左将二进制数每 3 位 分组,不足 3 位时在左侧补
0。 - 每组转换为对应的八进制数(
0-7)。
- 从右往左将二进制数每 3 位 分组,不足 3 位时在左侧补
- 示例:
- 二进制
1101011→ 分组为01101011(补零为001 101 011)→ 八进制153。
- 二进制
八进制转二进制
- 步骤:
- 每位八进制数转换为对应的 3 位二进制数(不足 3 位补前导
0)。 - 合并所有二进制组。
- 每位八进制数转换为对应的 3 位二进制数(不足 3 位补前导
- 示例:
- 八进制
72→7→111,2→010→ 二进制111010。
- 八进制
4. 其他进制转换(间接法)
- 十六进制 ↔ 十进制:
- 十六进制转十进制:按权展开(每位乘以
16^n)。 例:0x2A=2×16^1 + 10×16^0 = 42。 - 十进制转十六进制:除以 16 取余,余数
10-15对应A-F。 例:42 ÷ 16 = 2余10→ 十六进制2A。
- 十六进制转十进制:按权展开(每位乘以
- 八进制 ↔ 十进制:
- 八进制转十进制:按权展开(每位乘以
8^n)。 例:075=7×8^1 + 5×8^0 = 61。 - 十进制转八进制:除以 8 取余。 例:
61 ÷ 8 = 7余5→ 八进制75。
- 八进制转十进制:按权展开(每位乘以
二、各进制应用场景
1. 二进制(Base 2)
- 特点:仅用
0和1,计算机底层物理实现简单(电路通断、电平高低)。 - 应用场景:
- 计算机硬件(CPU 指令、内存存储)。
- 逻辑运算(布尔代数、位操作)。
- 通信协议(如 USB、以太网的底层信号)。
- 缺点:位数长,人类可读性差,需借助十六进制 / 八进制简化。
2. 十六进制(Base 16)
- 特点:1 位对应 4 位二进制,压缩二进制长度,便于书写和记忆。
- 应用场景:
- 编程(内存地址、变量地址,如
0x7FFFFFFF表示整数最大值)。 - 颜色表示(如
#FF0000代表红色,每两位对应 RGB 的一个分量)。 - 固件开发(二进制文件的十六进制转储,如
.hex文件)。 - 加密 / 哈希(如 MD5、SHA 的结果以十六进制显示)。
- 编程(内存地址、变量地址,如
3. 十进制(Base 10)
- 特点:人类习惯的进制,符合十进制计数法。
- 应用场景:
- 日常生活(货币、时间、数量)。
- 非计算机领域的数学运算(如财务、科学计算)。
- 程序中的输入输出(如用户输入的数字、打印结果)。
4. 八进制(Base 8)
- 特点:1 位对应 3 位二进制,早期用于简化二进制表示(现已逐渐被十六进制取代)。
- 应用场景:
- Unix/Linux 系统的文件权限(如
755表示读、写、执行权限)。 - 早期计算机系统(如 PDP-8,地址总线为 12 位,可表示为 4 位八进制数)。
- 部分嵌入式系统的配置参数(少数保留场景)。
- Unix/Linux 系统的文件权限(如
三、总结对比
| 进制 | 基数 | 核心用途 | 转换关键技巧 |
|---|---|---|---|
| 二进制 | 2 | 计算机底层、逻辑运算 | 分组(4 位→十六进制,3 位→八进制) |
| 十六进制 | 16 | 简化二进制、内存地址、颜色码 | 每位拆 / 合 4 位二进制 |
| 十进制 | 10 | 人类日常交互、非底层运算 | 除基取余、按权展开 |
| 八进制 | 8 | 历史遗留系统、文件权限 | 每位拆 / 合 3 位二进制 |
通过理解进制转换的规律和应用场景,可在编程、硬件开发、系统配置等场景中灵活切换进制,提升问题解决效率。
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客





