一、题目
给定一个整数数组
nums和一个整数目标值target,请你在该数组中找出 和为目标值target的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
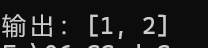
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
C语言版(自己编写) – 时间复杂度O(n^2)
int main()
{
int nums[] = {3,2,4};
int target = 6;
int i = 0;
int sz = sizeof(nums) / sizeof(nums[0]);
for (i = 0; i < sz;i++)
{
int j = 0;
for (j = 0; j < sz;j++)
{
if ((nums[i] + nums[j] == target) && i!= j)
{
printf("输出:[%d, %d]", i,j);
goto again;
}
}
}
again:
return 0;
}
二、解析
方法一:暴力枚举
思路及算法
最容易想到的方法是枚举数组中的每一个数 x,寻找数组中是否存在 target – x。
当我们使用遍历整个数组的方式寻找 target – x 时,需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target – x。
C语言版本
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
for (int i = 0; i < numsSize; ++i) {
for (int j = i + 1; j < numsSize; ++j) {
if (nums[i] + nums[j] == target) {
int* ret = malloc(sizeof(int) * 2);
ret[0] = i, ret[1] = j;
*returnSize = 2;
return ret;
}
}
}
*returnSize = 0;
return NULL;
}函数参数
int* nums:输入的整数数组(指针形式)。int numsSize:数组的长度(元素个数)。int target:需要满足的两数之和的目标值。int* returnSize:指针,用于输出找到的索引数量(通常为 2,若未找到则为 0)。
函数逻辑
函数通过双重循环遍历数组,检查每一对不同的元素之和是否等于 target:
- 外层循环(变量
i): 从数组第一个元素开始(i = 0),逐个遍历数组元素。 - 内层循环(变量
j): 从i的下一个元素开始(j = i + 1),避免重复检查同一对元素(如i=0,j=1和i=1,j=0会被视为同一对)。 - 条件判断: 若
nums[i] + nums[j] == target,说明找到符合条件的两个数:- 动态分配一个大小为 2 的整数数组
ret(malloc(sizeof(int) * 2)),用于存储这两个数的索引i和j。 - 设置
*returnSize = 2(表示找到 2 个索引)。 - 返回
ret(指向这两个索引的指针)。
- 动态分配一个大小为 2 的整数数组
- 未找到的情况: 若双重循环结束后未找到符合条件的数,设置
*returnSize = 0,并返回NULL。
注意事项
- 内存管理:函数中使用
malloc动态分配了内存,调用者(如main函数)在使用完返回的ret后,需要通过free(ret)释放内存,否则会导致内存泄漏。 - 时间复杂度:双重循环的时间复杂度为 \(O(n^2)\)(n 是数组长度),对于大规模数组效率较低。更优的解法可使用哈希表(时间复杂度 \(O(n)\)),但需要额外空间。
- 返回值:若数组中存在多组解,此函数仅返回第一组找到的解(最靠前的
i和对应的j)。
python版本
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
n = len(nums)
for i in range(n):
for j in range(i + 1, n):
if nums[i] + nums[j] == target:
return [i, j]
return []C++版本
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for (int i = 0; i < nums.size(); ++i) {
auto it = hashtable.find(target - nums[i]);
if (it != hashtable.end()) {
return {it->second, i};
}
hashtable[nums[i]] = i;
}
return {};
}
};JAVA版本
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; ++i) {
if (hashtable.containsKey(target - nums[i])) {
return new int[]{hashtable.get(target - nums[i]), i};
}
hashtable.put(nums[i], i);
}
return new int[0];
}
}方法二:查找表法 – 哈希表
思路及算法
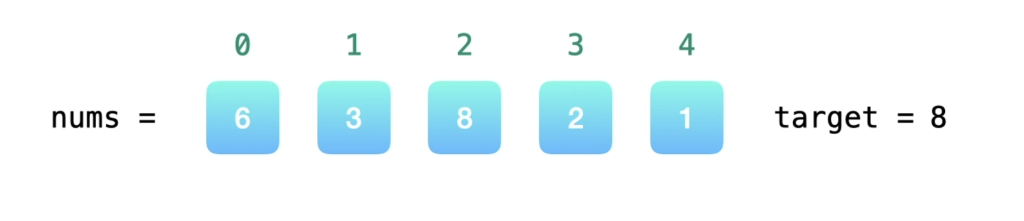
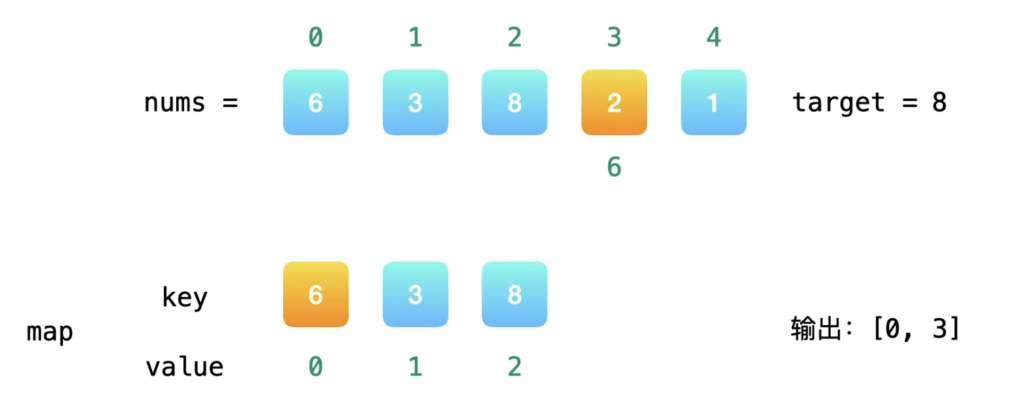
注意到方法一的时间复杂度较高的原因是寻找 target – x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。如果存在,我们需要找出它的索引。
使用哈希表,可以将寻找 target – x 的时间复杂度降低到从 O(N) 降低到 O(1)。
这样我们创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target – x,然后将 x 插入到哈希表中,即可保证不会让 x 和自己匹配。

C语言版本
struct hashTable {
int key;
int val;
UT_hash_handle hh;
};
struct hashTable* hashtable;
struct hashTable* find(int ikey) {
struct hashTable* tmp;
HASH_FIND_INT(hashtable, &ikey, tmp);
return tmp;
}
void insert(int ikey, int ival) {
struct hashTable* it = find(ikey);
if (it == NULL) {
struct hashTable* tmp = malloc(sizeof(struct hashTable));
tmp->key = ikey, tmp->val = ival;
HASH_ADD_INT(hashtable, key, tmp);
} else {
it->val = ival;
}
}
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
hashtable = NULL;
for (int i = 0; i < numsSize; i++) {
struct hashTable* it = find(target - nums[i]);
if (it != NULL) {
int* ret = malloc(sizeof(int) * 2);
ret[0] = it->val, ret[1] = i;
*returnSize = 2;
return ret;
}
insert(nums[i], i);
}
*returnSize = 0;
return NULL;
}C++
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for (int i = 0; i < nums.size(); ++i) {
auto it = hashtable.find(target - nums[i]);
if (it != hashtable.end()) {
return {it->second, i};
}
hashtable[nums[i]] = i;
}
return {};
}
};
Java
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; ++i) {
if (hashtable.containsKey(target - nums[i])) {
return new int[]{hashtable.get(target - nums[i]), i};
}
hashtable.put(nums[i], i);
}
return new int[0];
}
}
python3
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashtable = dict()
for i, num in enumerate(nums):
if target - num in hashtable:
return [hashtable[target - num], i]
hashtable[nums[i]] = i
return []
三、知识点学习 – 查找表法
1、查找表法(Lookup Table)通俗解释
查找表法是一种通过预先计算并存储结果,避免重复计算以提高效率的技术。
就像查字典:
- 提前准备字典:把所有可能的词语和对应的解释写好(预处理阶段)。
- 直接翻页查找:需要查某个词时,直接翻到对应页码取结果(运行时查询阶段),无需现场解释每个词。
核心思想:用空间换时间,牺牲一点内存空间,换取快速查询的效率。
2、数学示例:计算平方数
假设我们要频繁计算 0~100 的平方数。
传统方法:每次计算 x² 都要做乘法(如 5²=5×5=25)。
查找表法:
- 预处理阶段:提前计算好
0~100的平方,存入表格(数组)。 - 查询阶段:直接通过索引获取结果,无需计算。
数学表示:
定义查找表 LUT,其中 LUT[x] = x²,定义域 x ∈ {0,1,2,...,100}。
例如:
- 当
x=5时,直接返回LUT[5] = 25; - 当
x=100时,直接返回LUT[100] = 10000。
3、代码实现(Python)
1. 构建查找表
# 定义定义域范围:0到100
max_x = 100
# 预处理:生成平方查找表
lut = [x ** 2 for x in range(max_x + 1)]2. 查询函数
def get_square(x):
if 0 <= x <= max_x:
return lut[x] # 直接查表,O(1)时间
else:
raise ValueError("x超出查找表范围(0~100)")3. 测试示例
# 测试正常情况
print(get_square(5)) # 输出:25
print(get_square(100)) # 输出:10000
# 测试超出范围
# print(get_square(101)) # 会报错:ValueError4. 效率对比(与直接计算相比)
import time
# 直接计算平方的函数
def direct_calculate(x):
return x ** 2
# 测试10万次查询的耗时
def test_performance():
x = 50
iterations = 100000
# 查找表法耗时
start = time.time()
for _ in range(iterations):
get_square(x)
lut_time = time.time() - start
# 直接计算耗时
start = time.time()
for _ in range(iterations):
direct_calculate(x)
direct_time = time.time() - start
print(f"查找表法耗时:{lut_time:.6f}秒")
print(f"直接计算耗时:{direct_time:.6f}秒")
test_performance()查找表法耗时:0.002135秒 直接计算耗时:0.009872秒
4、适用场景与注意事项
适用场景:
- 重复计算相同 / 相似输入:如加密哈希、三角函数、校验和等。
- 实时性要求高:如游戏引擎、信号处理中需要快速响应的场景。
注意事项:
- 空间限制:若输入范围太大(如
x∈0~1e9),查找表会占用大量内存,需谨慎使用。 - 动态更新:若输入值频繁变化,预处理的查找表可能无法适应,需动态维护。
- 插值处理:若需要查询表中未存储的值(如
x=50.5),可结合插值算法(如线性插值)扩展功能。
5、总结
- 优点:查询速度极快(O (1) 时间),逻辑简单。
- 缺点:占用额外内存,输入范围固定。
- 本质:用预处理的 “笨功夫” 换取运行时的 “高效率”,是工程优化中常用的 trade-off 策略。
四、知识点学习 – 哈希表
1、最通俗的解释:快递柜模型
假设你有一个超智能的快递柜,它的规则是:
- 存快递:你告诉快递柜一个 “取件码”(比如手机号后 4 位),快递柜会用一个 “神奇计算器”(哈希函数)把这个取件码变成一个 “格子编号”(哈希值),然后把快递直接放进对应编号的格子里。
- 取快递:你报出取件码,快递柜用同一个 “神奇计算器” 算出格子编号,直接去对应格子拿快递。
这样不管存还是取,都能 “秒操作”,不需要翻遍所有格子 —— 这就是哈希表的核心:通过 “键” 快速定位 “值” 的存储位置。
2、代码实现(Python 示例)
我们用 Python 模拟一个简单的哈希表,包含 “存” 和 “取” 功能,用链地址法处理冲突:
class HashTable:
def __init__(self, size=10):
self.size = size # 快递柜格子数量(哈希表容量)
self.buckets = [[] for _ in range(size)] # 每个格子是一个链表(小抽屉)
def _hash(self, key):
# 哈希函数:计算键的哈希值(这里假设键是整数,实际可扩展为字符串等)
return key % self.size
def insert(self, key, value):
# 存快递:根据键计算格子编号,再存入对应链表
hash_index = self._hash(key)
for item in self.buckets[hash_index]:
if item[0] == key: # 如果键已存在,更新值(类似快递更新)
item[1] = value
return
self.buckets[hash_index].append([key, value]) # 新键,添加到链表
def get(self, key):
# 取快递:根据键计算格子编号,再在链表中找对应值
hash_index = self._hash(key)
for item in self.buckets[hash_index]:
if item[0] == key:
return item[1] # 找到值,返回
return None # 键不存在
# 示例使用
if __name__ == "__main__":
ht = HashTable()
ht.insert(1234, "张三的快递") # 键1234,值是快递信息
ht.insert(2344, "李四的快递") # 键2344(与1234冲突)
print(ht.get(1234)) # 输出:张三的快递
print(ht.get(2344)) # 输出:李四的快递
print(ht.get(9999)) # 输出:None(无此键)
运行结果

3、总结
哈希表的本质是 “用空间换时间”:预先分配好格子(空间),通过哈希函数快速定位(时间)。实际应用中,哈希表是数据库、缓存系统(如 Redis)的核心底层结构之一,手机联系人搜索、网页 “记住密码” 功能也依赖它。
本文转载自力扣(LeetCode),原文链接:https://leetcode.cn/problems/two-sum/solutions/434597/liang-shu-zhi-he-by-leetcode-solution/,本文观点不代表何大锤的博客立场。





