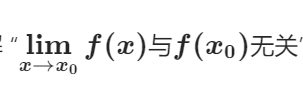导数
- 导数是研究变化快慢趋势的
- 极限是工具 – 研究函数变化趋势的
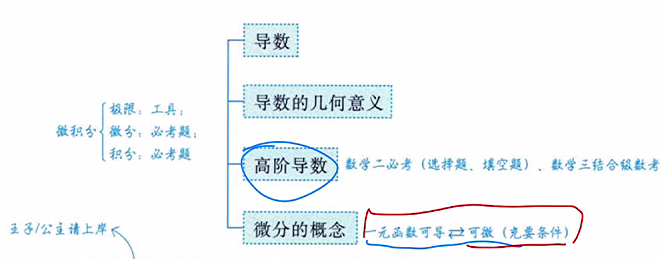
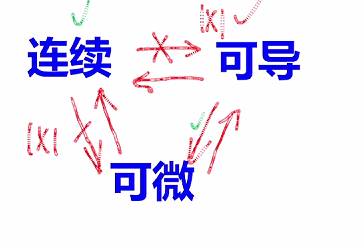
- 一元函数可导 与 可微 互为充要条件
一、基础知识结构
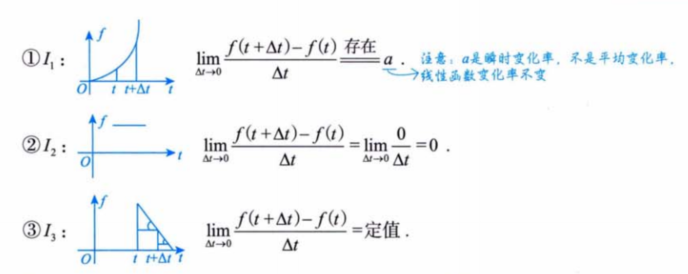
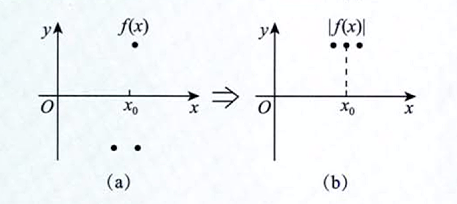
二、导数的定义
2.1 导数的概念

2.2 导数存在
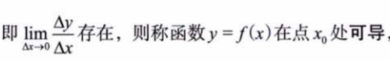

2.3 导数定义形式
1)增量式

2)函数式
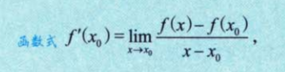
2.4 函数在一点可导的充要条件
1)单侧导数
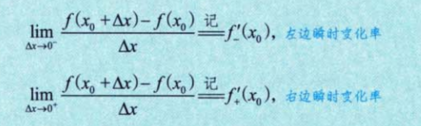
2)导数存在 – 极限问题
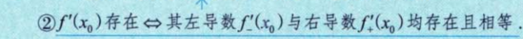
2.5 函数在一点可导的必要条件 – 可导必连续:


2.6 重要结论
2.6.1结论1

2.6.2 重要结论2

综上所述
一、“连续是点点相依相偎”
二、“导数不仅要点与点相依相偎,而且还需要导数极限存在”
三、总结条件强度
导数存在的条件,包含了连续的条件,且额外要求 “增量比的极限存在(左右导数一致等)” 。因此,导数存在是比连续更强的条件—— 能满足导数存在的函数,必然连续;但连续的函数,不一定能满足导数存在。
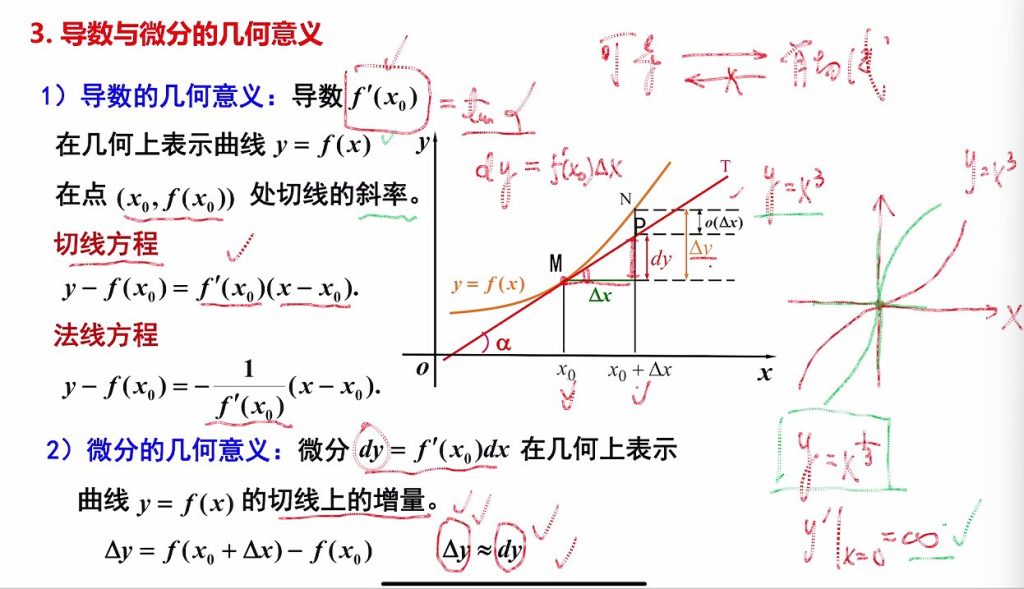
三、导数的几何意义
3.1 切线方程、法线方程

3.2 两个重要例子
切线存在导数不一定存在,导出存在切线一定存在
无穷导数在高等数学中 即为 不存在
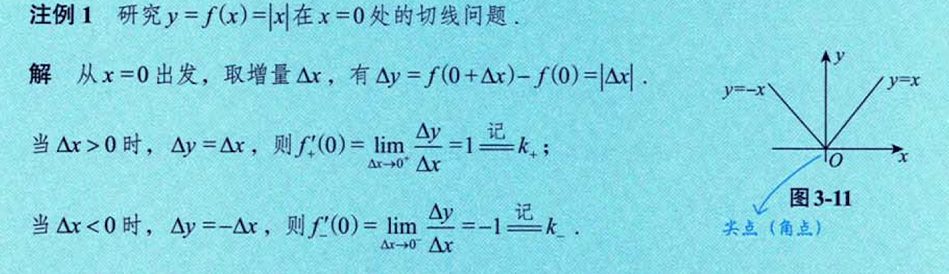

四、高阶导数
4.1 高阶导数的定义

4.2 高阶导数的重要结论


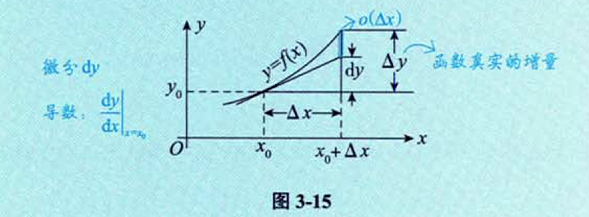
五、微分的概念
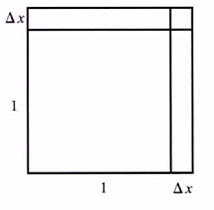
5.1 引例

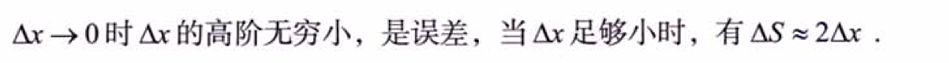
5.2 微分的定义



5.3 导数与微分的几何意义
5.4 连续,导数,可微之间的关系


本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客