一、常见题型
题目1、在数组A[0….n-1]中,查找给定值k的算法
// 题目1 在数组A中查找给定值k的算法
int main()
{
int A[10] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 11;
int i = sizeof(A) / sizeof(A[0]) - 1; //数组最后一个元素下标
int count = 0;
while (i >= 0 && (A[i] != k))
{
count++;
printf("i = %d , count = %d\n", i, count);
i--;
}
}
以下是代码运行结果
- A中没有元素与k相等的元素,i– 运行的频度是f(n) = n
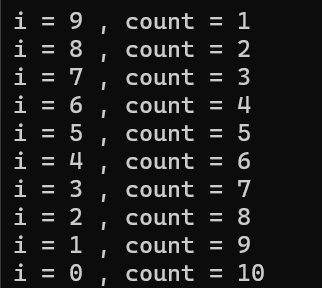
- A中最后一个元素与k相等,i– 运行的频度是f(n) = 0
题目2:计算下列代码的时间复杂度
void fun(int n)
{
int i = 0;
int count = 0;
while (i * i * i <= n)
{
i++;
count++;
printf("i=%d ", i);
}
printf("\ncount=%d ", count);
}
int main()
{
int n = 10;
fun(n);
}时间复杂度计算
- 关键操作:在
while循环里,i进行自增操作,同时count也进行自增,并且执行printf函数。 - 循环终止条件:当
i * i * i > n时,循环就会停止。 - 循环次数:假设循环执行的次数是
k,那么i的值会从 0 开始,逐步增加到k。此时,k要满足k³ > n,而(k-1)³ ≤ n。由此可知,k的大小和 n 的立方根是同一个数量级,即k ≈ ∛n。 - 时间复杂度:由于循环执行的次数和 n 的立方根成正比,所以该算法的时间复杂度为 O (∛n)。
结论
此算法的时间复杂度是O(n^(1/3))。
以下是代码运行结果:
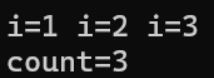
题目3:冒泡排序 – 计算下列代码的最坏时间复杂度
#include <stdio.h>
int main()
{
int i, j, temp;
int A[] = {9,8,7,6,5,4,3,2,1,0};
int count = 0;
int sz = sizeof(A) / sizeof(A[0]);
// 标准冒泡排序实现
for (i = 0; i < sz - 1; i++) {
for (j = 0; j < sz - i - 1; j++) {
if (A[j] > A[j + 1]) {
// 添加元素交换逻辑
temp = A[j];
A[j] = A[j + 1];
A[j + 1] = temp;
count++;
}
}
}
printf("count=%d\n", count);
// 打印所有元素
for (i = 0; i < sz; i++) {
printf("%d ", A[i]);
}
printf("\n");
return 0;
}时间复杂度推导
- 外层循环次数: 变量
i从sz-1递减到2,共执行 n-2 次(假设sz = n)。 - 内层循环次数: 对于每个
i,内层循环的次数为 i-1 次。具体来说:- 当
i = n-1时,内层循环执行 n-2 次; - 当
i = n-2时,内层循环执行 n-3 次; - …
- 当
i = 2时,内层循环执行 1 次。
- 当
- 总执行次数: 内层循环的总次数为等差数列求和: 1 + 2 + 3 + … + (n-2) = (n-2)(n-1)/2展开后为 (n² – 3n + 2)/2,忽略低阶项和系数,时间复杂度为 O(n²)。
关键结论
- 无论输入如何,嵌套循环的结构决定了代码的执行次数始终是二次函数,因此最坏、平均和最好时间复杂度均为 O(n²)。
- 排序逻辑缺陷:尽管代码中的赋值操作(
A[j] = A[j+1])无法正确排序数组,但时间复杂度仍由循环次数决定,与实际排序效果无关。
补充说明
- 若要实现正确的冒泡排序,需在交换元素时同时更新
A[j+1](例如使用临时变量),但这不会改变时间复杂度。 - 打印数组的循环(
for (i = 0; i < sz - 1; i++))仅执行 n-1 次,时间复杂度为 O(n),但整体复杂度仍由嵌套循环主导(O (n²))。
题目4:另一种形式的冒泡排序
#include <stdio.h>
int main()
{
int i, j, temp;
int A[] = {9,8,7,6,5,4,3,2,1,0};
int count = 0;
int sz = sizeof(A) / sizeof(A[0]);
// 修改:外层循环从 i=sz-1 开始递减到 1
for (i = sz-1; i > 0; i--) {
for (j = 0; j < i; j++) {
if (A[j] > A[j + 1]) {
temp = A[j];
A[j] = A[j + 1];
A[j + 1] = temp;
count++;
}
}
}
printf("count=%d\n", count);
// 打印所有元素
for (i = 0; i < sz; i++) {
printf("%d ", A[i]);
}
printf("\n");
return 0;
}1. 外层循环次数
- 循环条件:
i从sz-1(数组末尾索引)递减到1,共执行n-1次(n为数组长度,sz = n)。 - 示例:当
n=10时,i取值为9, 8, ..., 1,共循环 9 次。
2. 内层循环次数
- 对于每个外层循环的
i,内层循环j从0遍历到i-1,执行i次。 - 次数规律:
- 当
i = n-1时,内层循环执行n-1次; - 当
i = n-2时,内层循环执行n-2次; - ……
- 当
i = 1时,内层循环执行1次。
- 当
3. 总操作次数(数学推导)
- 内层循环总次数为等差数列求和:
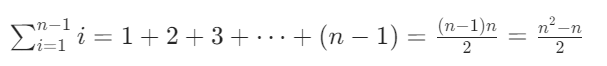
- 最高阶项为
n²,忽略低阶项和系数后,时间复杂度为 O(n²)。
4. 关键结论
| 场景 | 时间复杂度 | 说明 |
|---|---|---|
| 最坏情况 | O(n²) | 数组完全逆序(如示例输入),每轮均需完整比较和交换。 |
| 平均情况 | O(n²) | 随机无序数组,比较和交换次数接近最坏情况的一半。 |
| 最好情况 | O(n²) | 未优化时,即使数组有序,仍需执行所有比较(优化后可降至 O (n))。 |
最终结论
该冒泡排序代码的 最坏时间复杂度为 O (n²),由嵌套循环的二次方级操作次数决定。
实战题目


解析

数学解析

题目5:计算下列m++代码执行次数
int main()
{
int i = 0;
int j = 0;
int n = 10;
int m = 0;
for (i = 0;i <= n; i++)
{
for (j = 1;j <= 2 * i; j++)
{
m++;
}
}
printf("m = %d\n", m);
}以下是n=10计算结果:
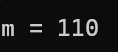

题目6:计算下列m++代码执行次数(对比题目5)
int main()
{
int i = 0;
int j = 0;
int n = 10;
int m = 0;
for (i = 0;i < n;i++)
{
for (j = 1;j < 2 * i;j++)
{
m++;
}
}
printf("m = %d\n", m);
}以下是运行结果:

(重要)总结以上该题型:


题目7:计算递归函数的时间复杂度
// 题目 11:递归函数的时间复杂度
int Func(int n)
{
if (n == 1)
return 1;
else
return 2 * Func(n / 2) + n;
}
int main()
{
int i = 4;
int ret = Func(i);
printf("%d\n", ret);
return 0;
}以下是运行结果:

解析
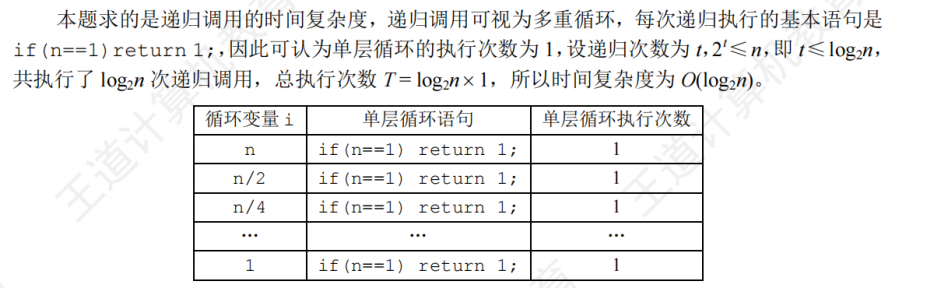

数学表达

二、408真题
题目1

解析
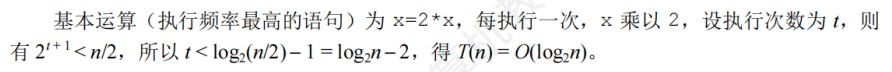
题目2

解析

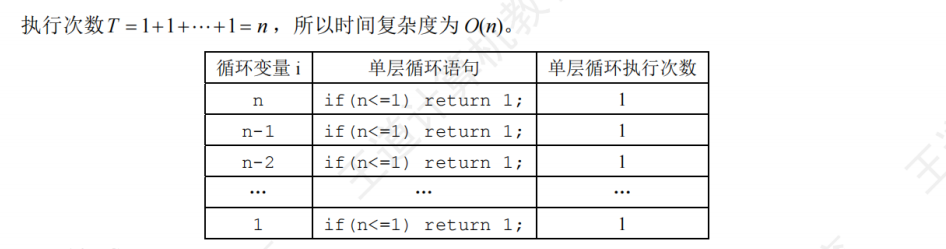
关键分析步骤:
- 递归调用次数:计算
fact(n)时,会依次调用fact(n-1)、fact(n-2)、… 直到fact(1)。总共有n次递归调用(从n递减到1,共n层)。 - 每次调用的操作量:每次递归调用仅执行一次乘法运算(
n * fact(n-1))和条件判断(n <= 1),均为常数时间O(1)。
结论
总时间复杂度为递归调用次数与单次操作时间的乘积,即:
时间复杂度 = O (n)(线性时间复杂度)。
题目3


解析

题目4
题目4

解析
int Func(int n)
{
int i = 0;
int sum = 0;
while (sum < n)
{
sum += ++i;
}
return sum;
}
int main()
{
int n = 4;
int ret = Func(n);
printf("%d\n", ret);
return 0;
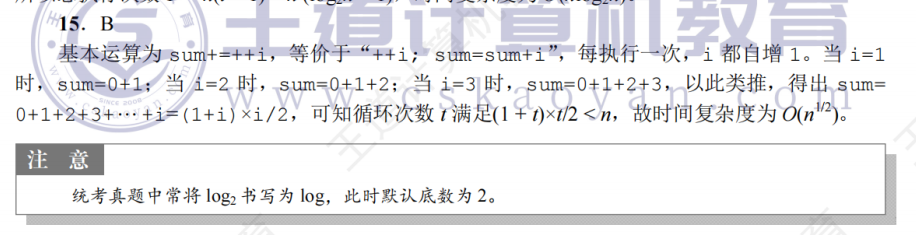
}要计算该代码的时间复杂度,我们需要分析Func函数中循环的执行次数与输入规模n的关系。
关键分析步骤:
- 循环逻辑:
while (sum < n)循环中,sum累加的是++i(即i先自增 1,再累加到sum)。因此,循环的实际行为是计算从 1 开始的连续整数的累加和,直到累加和大于等于n。 - 累加和公式:假设循环执行了
k次,则累加和为sum = 1 + 2 + 3 + ... + k = k(k+1)/2(等差数列求和公式)。 - 循环终止条件:循环终止时满足
sum >= n,即k(k+1)/2 >= n。当n较大时,近似有k² ≈ 2n,因此k ≈ √(2n)(k与n的平方根成正比)。
时间复杂度结论:
循环的执行次数k与n的平方根成正比,因此时间复杂度为 O(√n)(根号 n 阶)。
题目5

解析
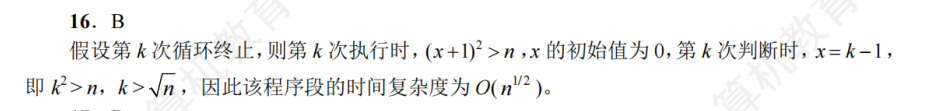
题目6

解析


题目7

解析

三、总结

本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客





