一、数据结构的基本概念(王道)

1、可以用抽象数据类型定义一个完整的数据结构
抽象数据类型ADT – 描述数据的逻辑结构和抽象运算,通常用数据对象,数据关系,基本操作集来表示定义一个完整的数据结构。
抽象数据类型(Abstract Data Type, ADT)是一种编程概念,它只关注数据 “能做什么”(功能),而不关心 “如何实现”(细节)。可以理解为 “黑箱”:用户只需要知道可以调用哪些操作(比如 “添加元素”“删除元素”),不需要知道这些操作内部是怎么完成的。
举个生活化的例子:你用手机打电话时,只需要知道按 “拨号键” 能拨出电话(功能),不需要知道手机内部是如何处理信号、连接基站的(实现细节)。这里的 “电话功能” 就类似 ADT 的定义。
ADT 的核心是封装(隐藏实现)和定义接口(暴露功能)
2、非线性数据结构 – 树和图、集合;线性数据结构 – 一般线性表、栈、队列、串、数组
数据的逻辑结构分为线性和非线性
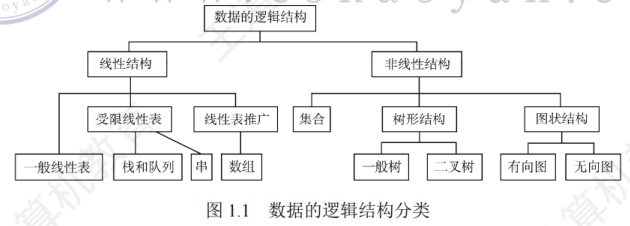
逻辑结构是指数据元素之间的逻辑关系,即从逻辑结构关系上描述数据;它与数据的存储无关,独立于计算机
3、顺序表、哈希表、单链表 – 既描述数据结构,又描述存储结构和运算;
有序表属于逻辑结构仅描述元素之间的逻辑关系,既可以链式存储,也可以顺序存储
4、数据结构三要素:逻辑结构、存储结构(物理结构)、数据运算
逻辑结构与存储结构的区别
数据的逻辑结构从面向实际问题出发,抽象表达,独立于存储结构;
数据的存储结构是逻辑结构在计算机上的映射,不能独立于逻辑结构
5、在存储数据时,不仅要存储数据元素的值,而且要存储数据元素之间的关系
6(应用题)、对于两种不同的数据结构,逻辑结构或者物理结构一定不相同吗?
答案
数据的运算也是数据结构的一个重要方面。
对于两种不同的数据结构,它们的逻辑结构和物理结构完全有可能相同。比如二叉树和二叉排序树,二叉排序树可以采用二叉树的逻辑表示和存储方式,前者通常用于表示层次关系,而后者通常用于排序和查找。虽然它们的运算都有建立树、插入结点、删除结点和查找结点等功能,但对于二叉树和二叉排序树,这些运算的定义是不同的,以查找结点为例,二叉树的平均时间复杂度为 O(n),而二叉排序树的平均时间复杂度为 O(logn)。
逻辑结构与物理结构的独立性
- 逻辑结构相同,物理结构不同:如顺序表与链表。
- 物理结构相同,逻辑结构不同:如用链式存储的二叉树与图。
- 因此,两种不同的数据结构可能在逻辑结构或物理结构上存在相同点,并非一定完全不同。
结构定义
- 二叉树:每个节点最多有两个子节点(左子节点和右子节点),子节点的顺序可以任意,没有特定的排列要求。
- 二叉排序树(BST):是一种特殊的二叉树,每个节点的值需满足:
- 左子树上所有节点的值均小于该节点的值;
- 右子树上所有节点的值均大于该节点的值;
- 左右子树也分别为二叉排序树。
// 二叉树的节点可以随意排列,例如
1
/ \
3 2
/ \
5 4
// 二叉排序树的节点必须满足左小右大的顺序,例如:
3
/ \
1 4
\ \
2 57、试举一例,说明对于相同的逻辑结构,同一种运算在不同的存储方式下实现时,其运算效率不同。
答案
线性表:顺序存储方式、链式存储方式。
在顺序存储方式下,在线性表中插入和删除元素,平均要移动近一半的元素,时间复杂度为O(n);
在链式存储方式下,插入和删除的时间复杂度为O(1)。
| 知识要点补充 | 说明 | 备注 |
| 数据 | 信息载体 | |
| 数据元素 | 数据基本单位 | 逻辑、物理(存储) |
| 数据对象 | 相同性质的数据元素集合 | 数据的子集 |
| 数据类型 | 原子、结构、抽象 | |
| 数据结构三要素 | 逻辑、物理(存储)、数据运算 | |
| 逻辑结构 | 集合、线性结构、树形结构、图结构(网状结构) | |
| 存储结构 | 顺序存储、链式存储、索引存储、散列存储(Hash存储) |
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客





