一、什么是空间复杂度?
算法效率的度量 = 时间复杂度 + 空间复杂度
其中空间复杂度就是用于衡量算法在运行过程中所需占用的额外存储空间,即空间开销(内存开销)
空间复杂度表示方法:S(n)
二、 案例汇总
案例1:空间复杂度S(n) =O(1)
#include <stdio.h>
// 输入正整数的代码
int main()
{
int n;
printf("请输入一个正整数n:");
if (scanf("%d", &n) != 1 || n < 0) //scanf 函数的返回值是成功匹配并赋值的输入项数量
{
printf("错误:n 必须为正整数。\n");
return 1; // 非零返回值(如 return 1;):表示程序异常结束,常用于指示发生了错误。
}
// 使用等差数列求和公式,空间复杂度为 O(1)
int sum = n * (n + 1) / 2;
printf("从 1 到 %d 的整数之和为: %d\n", n, sum);
return 0;
}- 上述代码执行结果:

- 空间复杂度分析:
- 程序中只使用了固定的几个变量(
n和sum),无论输入值n多大,额外占用的内存空间都是恒定的。 - 没有动态分配内存,也没有使用与
n相关的数组或其他数据结构,因此空间复杂度为 O (1)。
- 程序中只使用了固定的几个变量(
案例2:空间复杂度S(n) =O(n)
这段代码创建了一个大小为 n 的整数数组,对其进行初始化并计算所有元素的和,以此展示 O (n) 空间复杂度的应用。
#define _CRT_SECURE_NO_WARNINGS
// 使用 C 语言实现的空间复杂度为 O (n) 的示例代码,
// 该代码创建一个包含 n 个元素的数组,并计算其累加和:
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n = 10;
int* arr;
int sum = 0;
int i;
// 动态分配 n 个整数的空间
arr = (int*)malloc(n * sizeof(int));
if (arr == NULL)
{
printf("内存分配失败\n");
return 1;
}
// 初始化数组元素
for (i = 0; i < 10; i++)
{
arr[i] = i + 1;
}
// 遍历数组元素
for (i = 0; i < 10; i++)
{
printf("arr[%d]=%d ", i, arr[i]);
}
// 计算数组元素的累加和
for (i = 0; i < 10; i++)
{
sum += arr[i];
}
printf("数组元素的累加和为: %d\n", sum);
free(arr); //释放动态分配的内存
return 0;
}- 上述代码执行结果:

- 空间复杂度分析:
- 动态分配了一个大小为
n的整数数组,因此空间复杂度为 O (n)。 - 其他变量(如
sum、i)的空间复杂度为 O (1),不影响总体复杂度。
- 动态分配了一个大小为
结论
- 空间复杂度只需要关注存储空间大小与问题规模相关的变量
案例3:空间复杂度S(n) =O(n × n )
#include <stdio.h>
#include <stdlib.h>
int main() {
int n = 5; // 矩阵大小
int **matrix;
int i, j;
// 动态分配 n×n 的二维数组
matrix = (int **)malloc(n * sizeof(int *));
if (matrix == NULL) {
printf("内存分配失败\n");
return 1;
}
for (i = 0; i < n; i++) {
matrix[i] = (int *)malloc(n * sizeof(int));
if (matrix[i] == NULL) {
printf("内存分配失败\n");
return 1;
}
}
// 初始化矩阵:将每个元素设为行号和列号的乘积
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
matrix[i][j] = i * j;
}
}
// 打印矩阵
printf("生成的 %dx%d 矩阵:\n", n, n);
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
printf("%4d", matrix[i][j]);
}
printf("\n");
}
// 计算矩阵所有元素的和
int sum = 0;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
sum += matrix[i][j];
}
}
printf("矩阵元素的总和为:%d\n", sum);
// 释放动态分配的内存(按分配的相反顺序释放)
for (i = 0; i < n; i++) {
free(matrix[i]);
}
free(matrix);
return 0;
}- 上述代码执行结果:
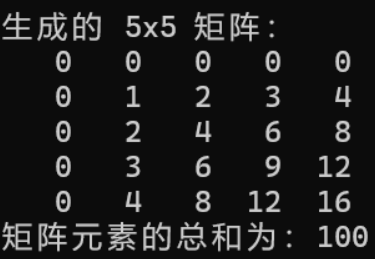
- 空间复杂度分析:
- 分配了一个
n × n的二维数组,总元素数量为n²。 - 每个元素占用一个整数的空间,因此总空间为 O (n²)。
- 分配了一个
其他空间复杂度为S(n) = n × n的情况
二维网格 / 棋盘:
// 创建 n×n 的棋盘,初始化为全 0(空白)
int **board = (int **)malloc(n * sizeof(int *));
for (i = 0; i < n; i++) {
board[i] = (int *)malloc(n * sizeof(int));
for (j = 0; j < n; j++) {
board[i][j] = 0; // 0 表示空白,1 可表示棋子
}
}邻接矩阵(图的表示):
// 用 n×n 矩阵表示图的邻接关系
int **graph = (int **)malloc(n * sizeof(int *));
for (i = 0; i < n; i++) {
graph[i] = (int *)malloc(n * sizeof(int));
for (j = 0; j < n; j++) {
graph[i][j] = 0; // 0 表示无边,1 表示有边
}
}案例4:递归型
- 先写结论:递归函数的空间复杂度主要取决于递归调用栈的深度,即递归过程中最多同时存在多少层未返回的函数调用。
- 1. 空间复杂度的核心因素
- 递归函数的空间消耗主要来自:
- 调用栈空间:每次递归调用都会在栈上分配一个新的栈帧(Stack Frame),包含局部变量、返回地址等。
- 其他辅助空间:函数内部使用的额外数据结构(如数组、列表等)。
- 递归函数的空间消耗主要来自:
- 空间复杂度 = 递归调用栈的深度 × 每层栈帧的空间消耗
4.1 线性递归(如阶乘)
int factorial(int n) {
if (n <= 1) return 1; // 基线条件
return n * factorial(n-1); // 递归调用
}- 调用栈深度:
n层(从factorial(n)到factorial(1))。 - 每层空间:常数级(仅保存
n和返回地址)。 - 空间复杂度:O(n)。
4.2 尾递归(优化后的阶乘)
int factorial_tail(int n, int acc) {
if (n <= 1) return acc; // 基线条件
return factorial_tail(n-1, n * acc); // 尾递归调用
}- 特点:递归调用是函数的最后一步操作,编译器可优化为循环(尾递归消除)。
- 优化后空间:若编译器支持,空间复杂度降为 O(1)(仅需一层栈帧)。
4.3二叉树遍历(如中序遍历)
void inorder(Node* root) {
if (root == NULL) return;
inorder(root->left); // 递归左子树
printf("%d ", root->val);
inorder(root->right); // 递归右子树
}- 最坏情况:二叉树退化为链表,递归深度为树的高度
h。 - 空间复杂度O(h),其中为树的高度。
- 对于完全二叉树,
h = O(log n),空间复杂度为 O(log n)。 - 对于退化为链表的树,
h = O(n),空间复杂度为 O(n)。
- 对于完全二叉树,
4.4分治递归(如归并排序)
void merge_sort(int arr[], int left, int right) {
if (left >= right) return;
int mid = left + (right - left) / 2;
merge_sort(arr, left, mid); // 递归左半部分
merge_sort(arr, mid+1, right); // 递归右半部分
merge(arr, left, mid, right); // 合并结果
}- 递归深度:每次递归将问题规模减半,递归树的高度为
log n。 - 每层空间:合并操作需要辅助数组(
O(n)),但这些数组在递归返回后会被释放。 - 空间复杂度:递归栈深度为 O(log n),但合并操作的辅助数组导致总空间为 O(n)。
4.5斐波那契数列
int fib(int n) {
if (n <= 1) return n;
return fib(n-1) + fib(n-2);
}- 空间复杂度:O (n)(递归树的最大深度)。
- 问题:存在大量重复计算,时间复杂度为 O (2ⁿ)。
4.6迭代实现
int fib_iter(int n) {
if (n <= 1) return n;
int a = 0, b = 1, c;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}- 空间复杂度:O (1)(仅需常数级变量)。
三、常见数据结构空间复杂度
| 算法 / 数据结构 | 典型场景 | 空间复杂度 | 说明 |
|---|---|---|---|
| 递归算法 | 阶乘、斐波那契数列(递归版) | (O(n)) | 空间复杂度由递归栈深度决定,最坏情况下递归深度为 n(如单支递归树)。 |
| 二叉树递归遍历 | 前序、中序、后序遍历(递归实现) | (O(h)) | h 为树的高度,最坏情况下 (h = n)(退化为链表的树),平均 (O(\log n))。 |
| 快速排序 | 原地排序(递归实现) | (O(\log n)) | 递归栈深度平均为 (O(\log n)),最坏情况下退化为 (O(n))(需优化随机化)。 |
| 归并排序 | 合并两个有序数组或链表 | (O(n)) | 需要额外的 (O(n)) 空间存储临时合并结果。 |
| 堆排序 | 原地建堆排序 | (O(1)) | 仅使用常数级额外空间(不考虑输入数组本身)。 |
| 二分查找 | 有序数组查找 | (O(1)) | 迭代实现仅用常数空间;递归实现需 (O(\log n)) 栈空间(较少考递归版)。 |
| 广度优先搜索(BFS) | 图或树的层次遍历 | (O(n)) | 队列中最多存储 n 个节点(最坏情况为完全二叉树或图的所有节点)。 |
| 深度优先搜索(DFS) | 图或树的递归遍历 | (O(h)) | 递归栈深度等于树的高度或图的深度,最坏 (O(n))。 |
| 动态规划 | 斐波那契数列(数组存储中间结果) | (O(n)) | 用数组存储前 n 项,可优化为 (O(1))(滚动变量)。 |
| 字符串匹配(KMP 算法) | 构建 next 数组 | (O(m)) | m 为模式串长度,需额外数组存储 next 数组。 |
| 基数排序 | 按位排序(非比较排序) | (O(n + k)) | k 为位数,需临时存储桶数组,空间与数据范围相关。 |
| 计数排序 | 数据范围较小的排序 | (O(k)) | k 为数据范围,需额外数组统计频率。 |
| 哈希表(散列表) | 存储键值对 | (O(n)) | 存储 n 个元素的额外空间(不考虑负载因子的影响)。 |
| 链表反转(递归) | 递归反转单链表 | (O(n)) | 递归栈深度为 n,迭代实现为 (O(1))。 |
四、关于计算空间复杂度结论&易错点
- 递归算法的空间复杂度
- 直接由递归调用栈的最大深度决定,与问题规模 n 的关系需结合递归树形态。
- 例:快速排序平均递归深度 (O(\log n)),最坏 (O(n))(需通过随机化避免最坏情况)。
- 原地算法(In-Place)
- 指仅使用 (O(1)) 额外空间的算法,如堆排序、插入排序、选择排序。
- 误区:快速排序是 “原地排序”(指空间复杂度为 (O(1)) ?×)—— 错! 快速排序的额外空间来自递归栈,其空间复杂度为 (O(\log n))(平均),严格来说不属于 (O(1)) 原地算法,但常被称为 “原地排序”(此处 “原地” 指不依赖额外存储,但递归栈仍占空间)。
- 动态规划的空间优化
- 若状态转移仅依赖前 k 项(如斐波那契数列),可通过滚动变量将空间从 (O(n)) 优化至 (O(1))。
- 图算法的空间复杂度
- BFS 和 DFS 的空间复杂度均与图的存储方式无关(邻接表或邻接矩阵),仅取决于遍历过程中存储节点的数量。
- 邻接表的空间复杂度为 (O(n + m))(存储图本身),但这是输入空间,不计入算法的额外空间复杂度。
- 非比较排序的空间特性
- 基数排序、计数排序的空间复杂度与数据范围相关,可能高于 (O(n)),需根据题目条件判断。
五、典型例题分析
例 1:递归实现的斐波那契数列
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)- 空间复杂度:(O(n))(递归栈深度为 n,形成单支树)。
例 2:归并排序(递归实现)
- 每次合并需 (O(n)) 额外空间,但空间可重复利用,总空间复杂度为 (O(n))。
例 3:二叉树层序遍历(迭代实现)
- 使用队列存储节点,最坏情况下队列存储 n 个节点,空间复杂度为 (O(n))。
六、备考建议
- 区分输入空间与额外空间:空间复杂度仅计算算法运行时新增的空间,不包括输入数据本身。
- 递归优先看栈深度:遇到递归算法,先分析递归树的最大深度。
- 记住常考算法的固定结论:如快排、归并、堆排、DFS/BFS 的空间复杂度是高频考点。
- 注意空间优化场景:动态规划、链表操作中常考空间优化后的复杂度(如 (O(1)) 空间的斐波那契数列)。
本网站原创文章版权归何大锤的狂飙日记所有。发布者:何大锤,转转请注明出处:何大锤的博客





