一、高等数学部分

第一部分 极限部分

第二部分 微分学

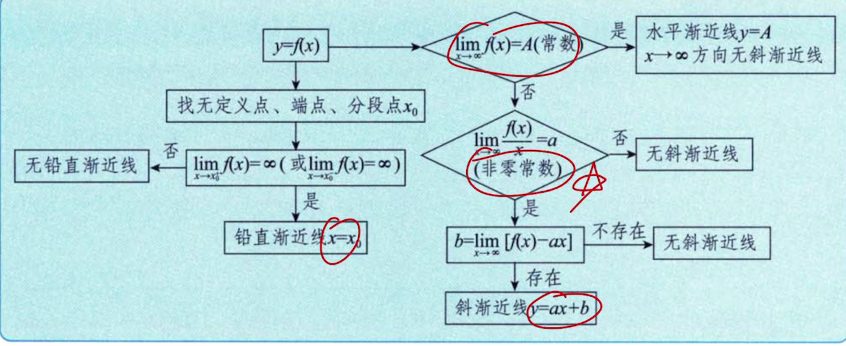
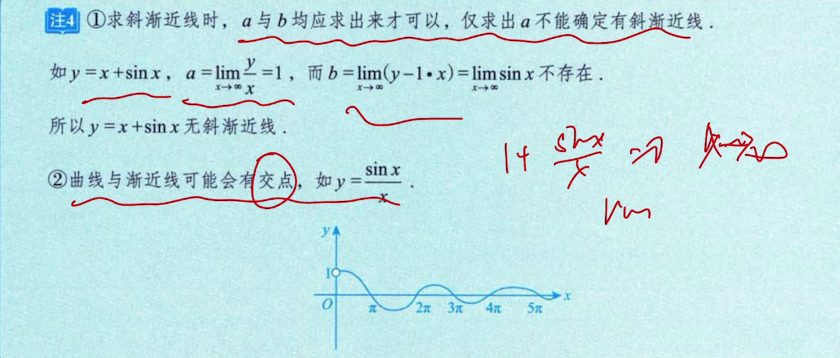
渐近线

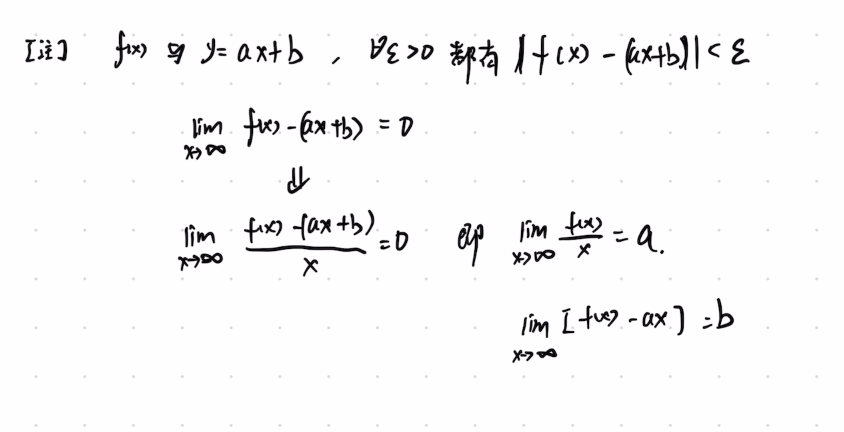
第三部分 积分学

3.1 不定积分

3.1.1 原函数存在定理

3.1.2 f(x)存在 与 f'(x) 存在的几个重要结论

3.1.3 中值定理、介质定理、达布定理

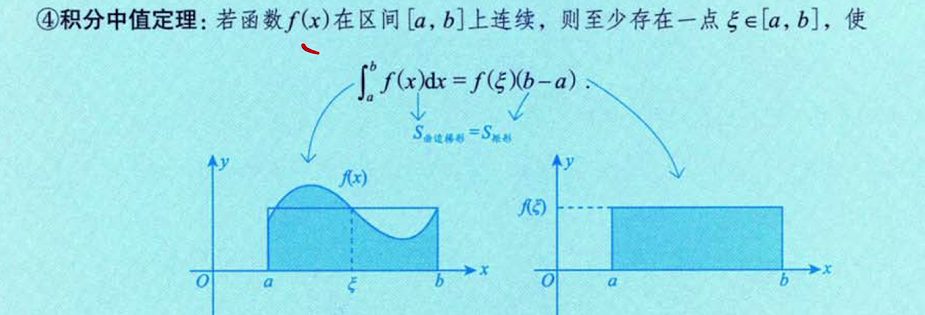
积分中值定理

介值定理

达布定理

3.1.4 原函数F(x)处处可导的几个结论

3.1.5 常见的含有振荡间断点的函数

3.3 不定积分公式

3.3.1 常用积分公式

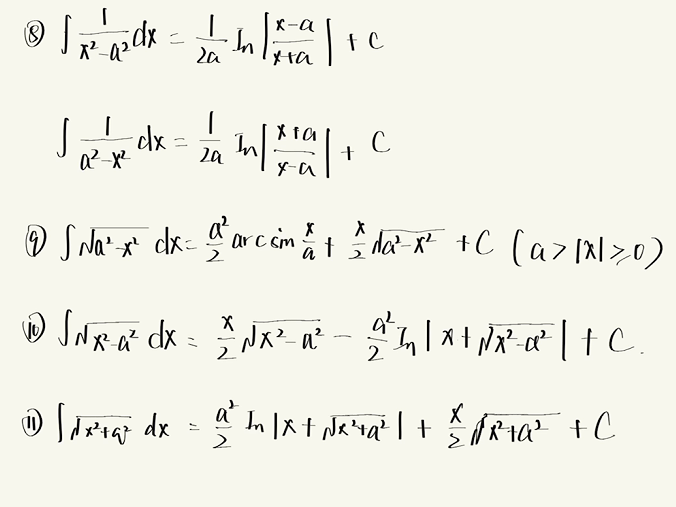
3.3.2 补充不定积分公式

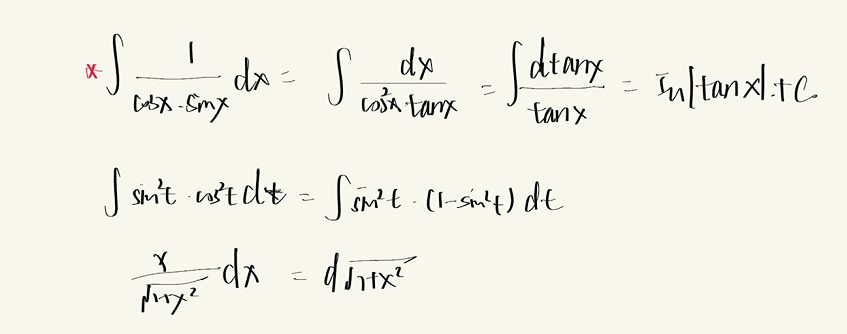
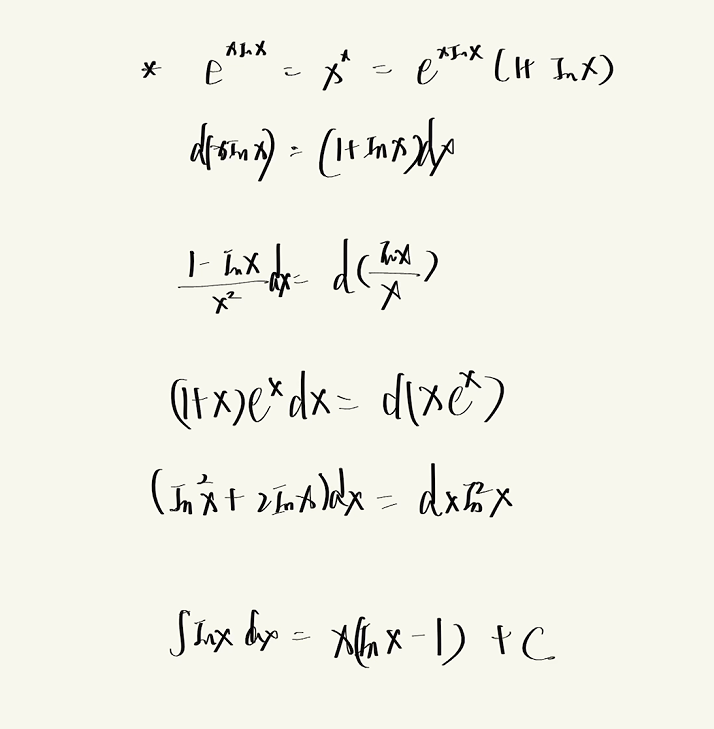
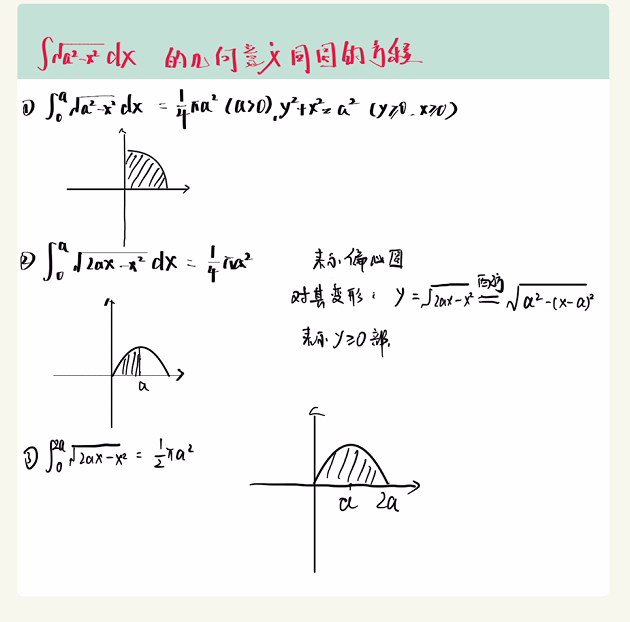
3.3.3 积分的几何意义

3.4 定积分公式

3.4.1 常用定积分公式及性质

奇偶性、周期性

区间再现

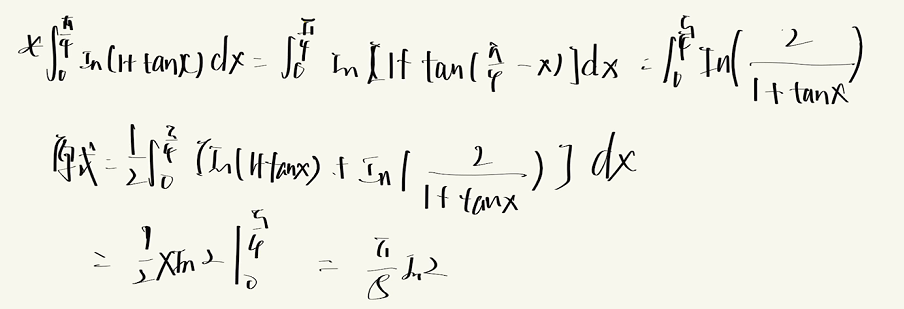
华里士公式

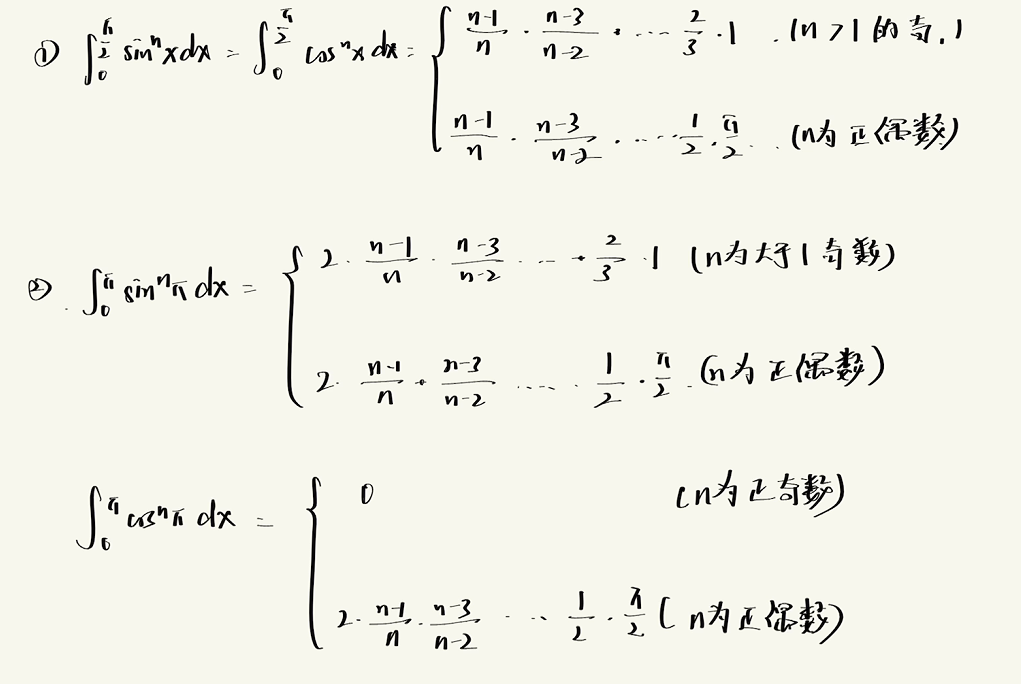
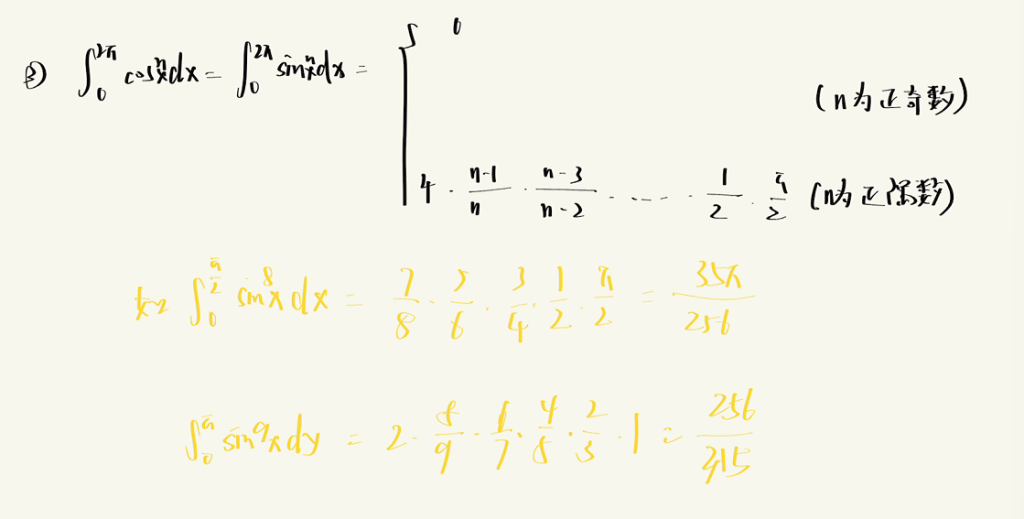
重要公式

3.4.2 定积分公式补充

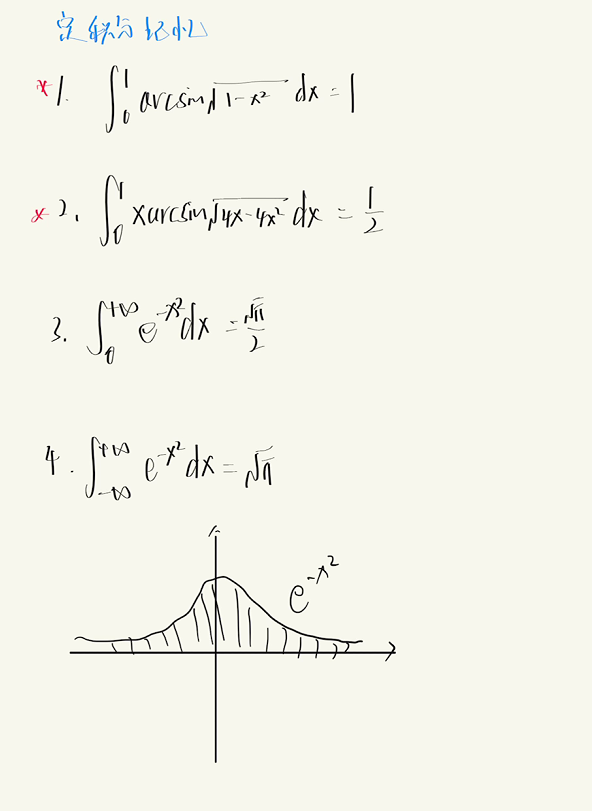
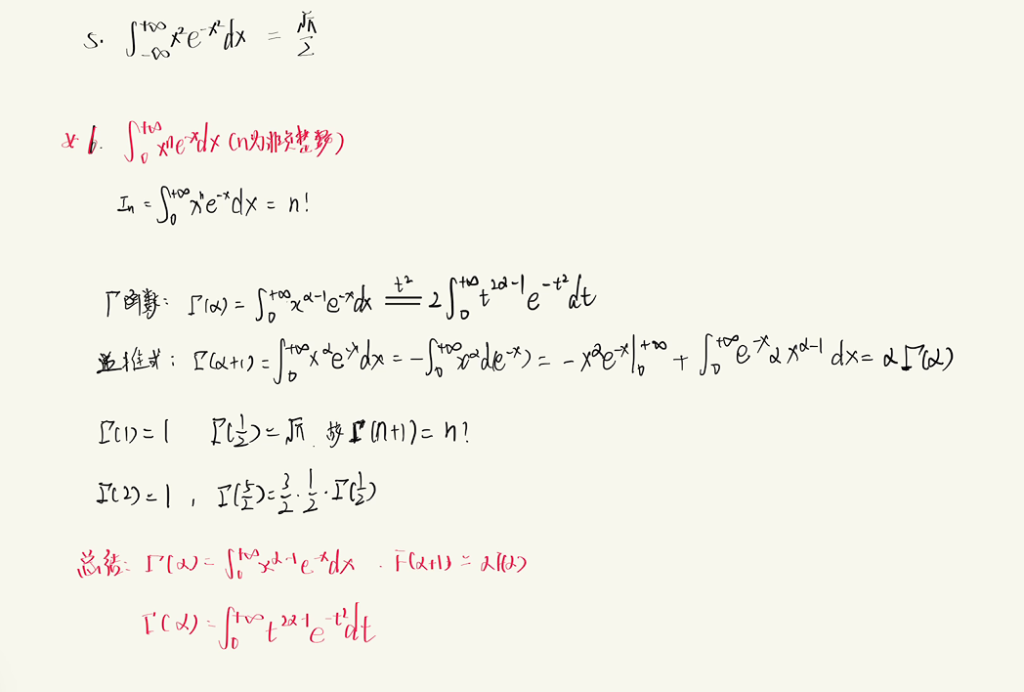
3.5 变限积分公式及性质

基本公式

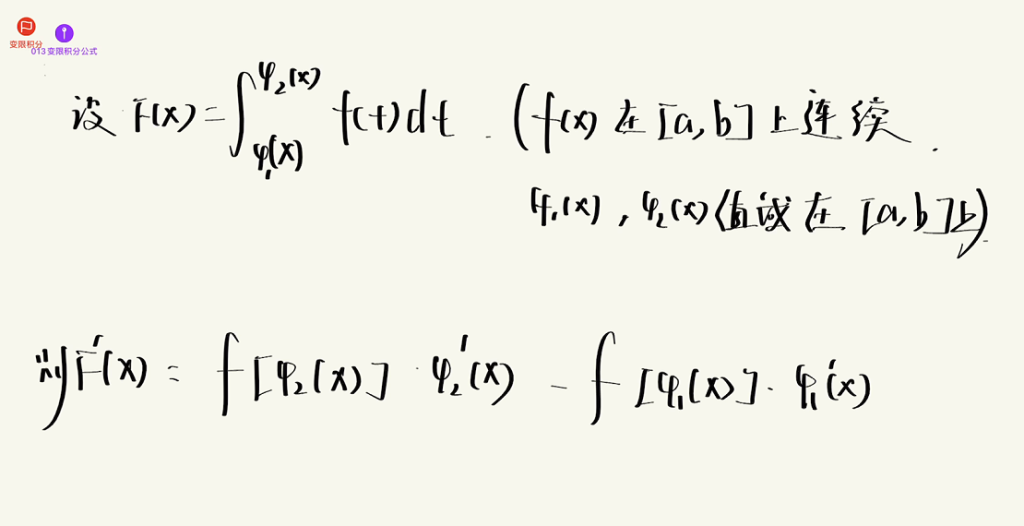
重要性质

3.6 积分方法

3.6.1 凑微分法

3.6.2 换元法

3.6.3 分部积分法

3.6.4 有理函数积分

3.6.5 三角函数有理式积分

3.6.6 定积分积分方法

牛顿莱布尼茨公式

定积分换元

定积分分部积分法

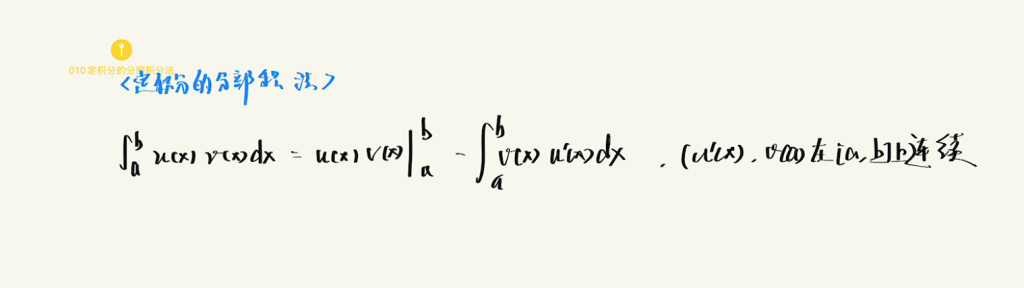
3.6.7 积不出函数

第四部分 微分方程

4.1 一阶微分方程

4.2 二阶可降阶微分方程

4.3 全微分方程

4.4 高阶线性微分方程

4.5 待定系数法求非齐次特解

形式一

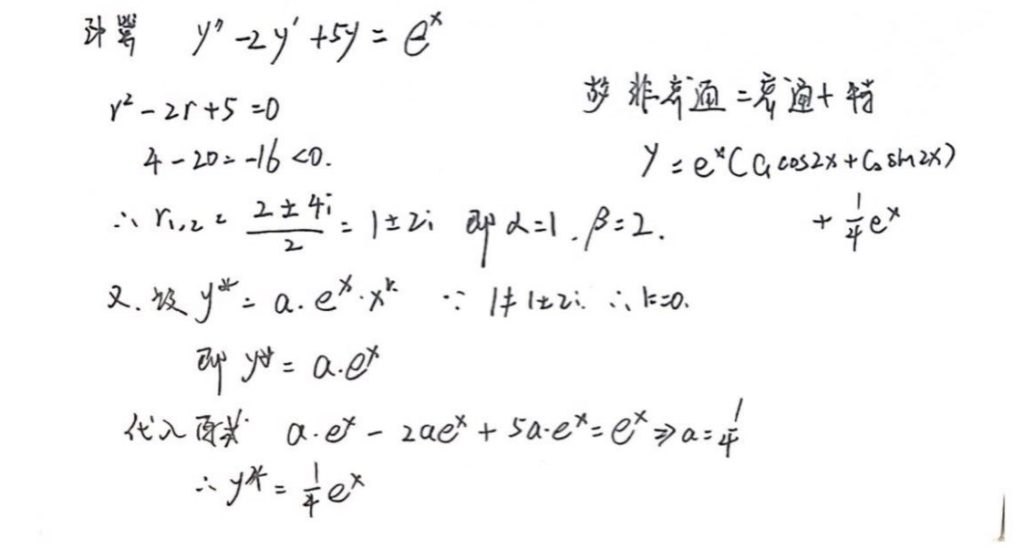
形式二

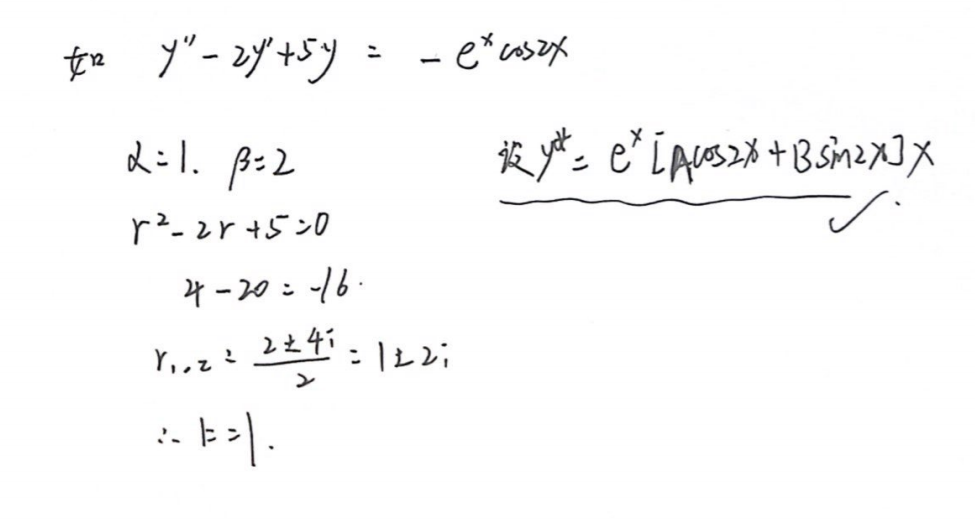
4.6 微分算子法求非齐次的特解

形式一

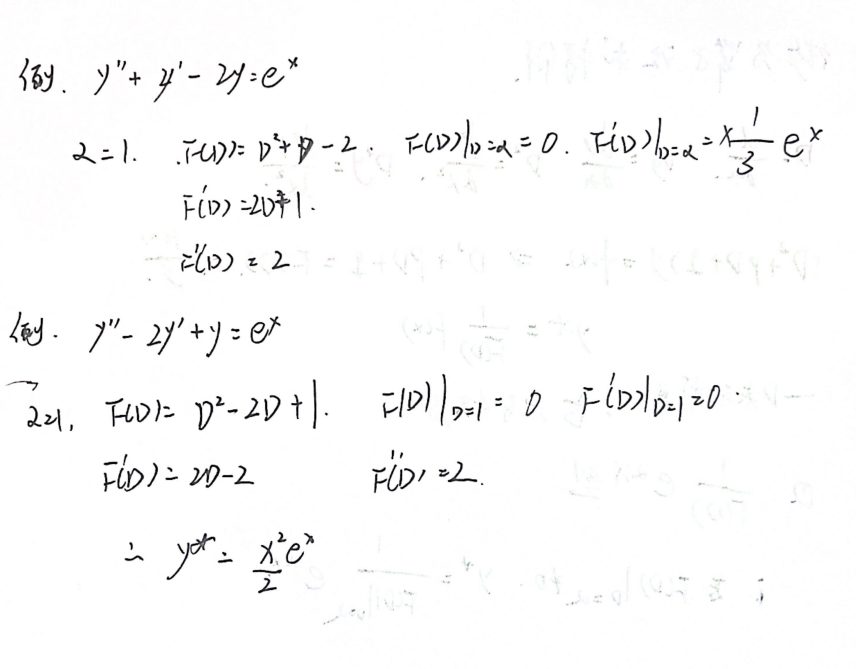
形式二

形式三

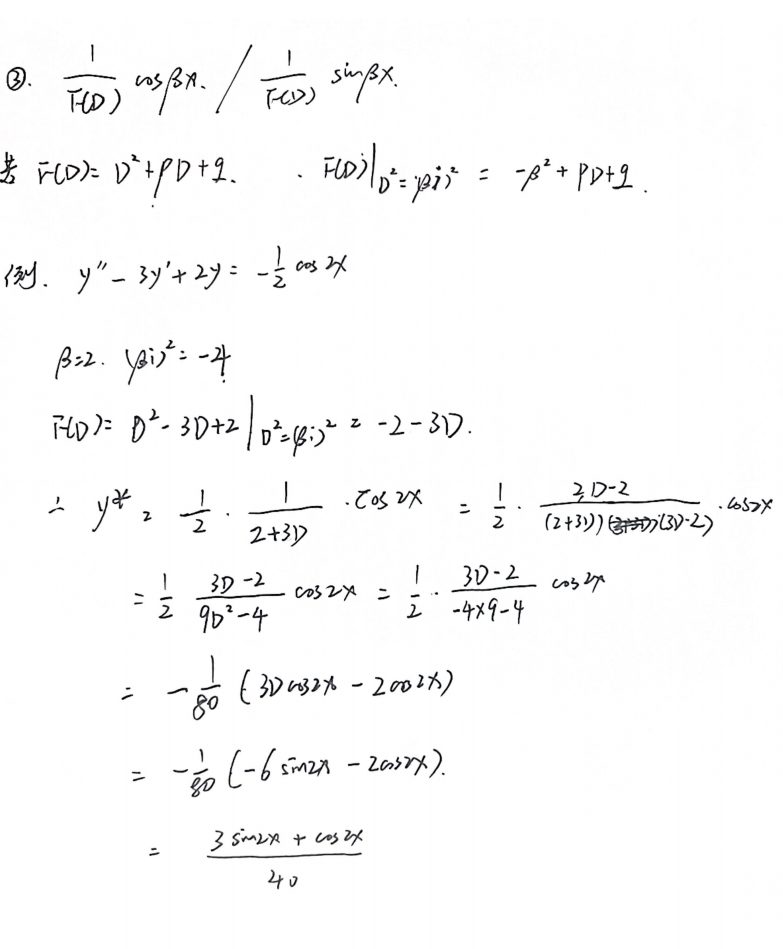
形式四

形式五

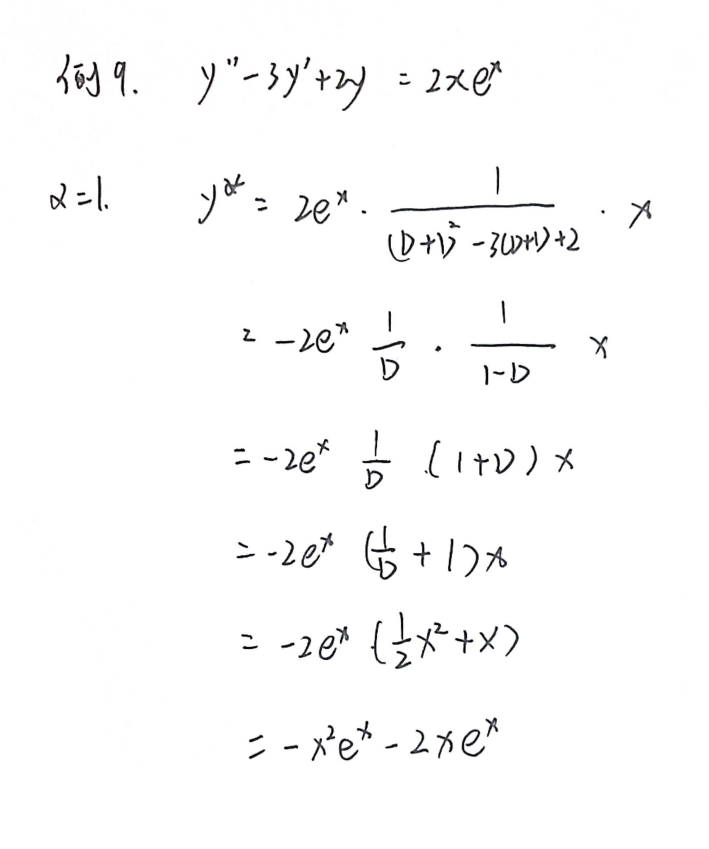
4.7 非齐次的通解

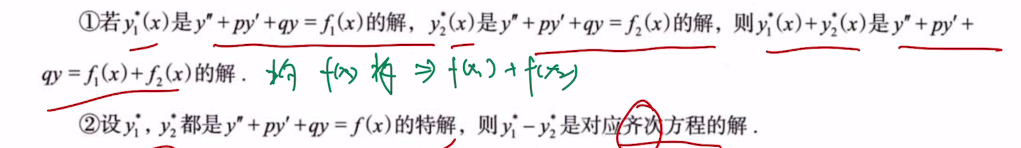
4.8 n（n>2）阶常系数齐次线性微分方程

4.9 欧拉方程

注意一定要区分x>0还是x<0，最后结果也需要回代

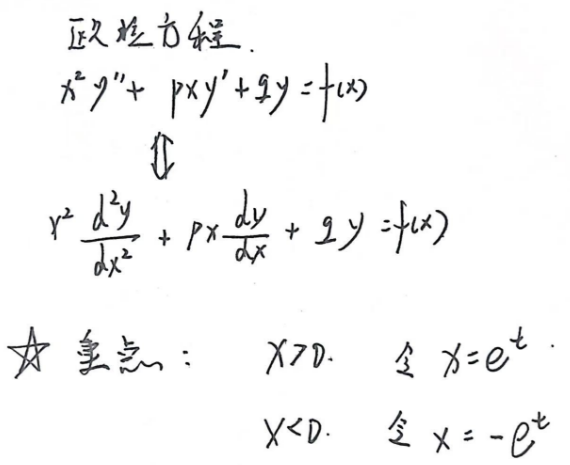
x>0

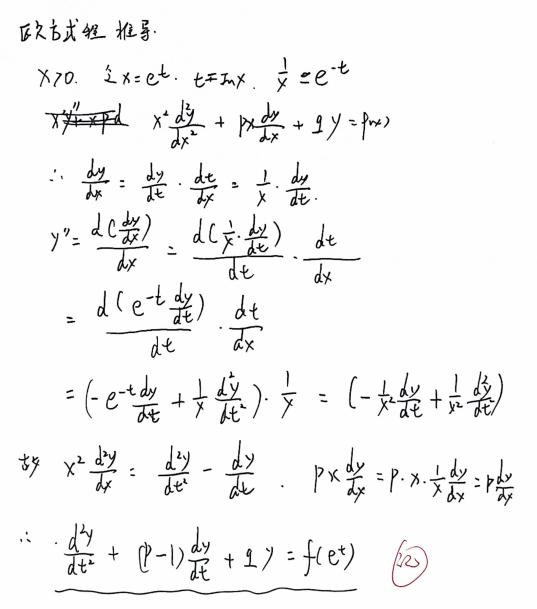
x<0

4.10 线性微分方程解的结构

第五部分 无穷级数

5.1 常数项级数的概念

5.2 常数项级数的性质

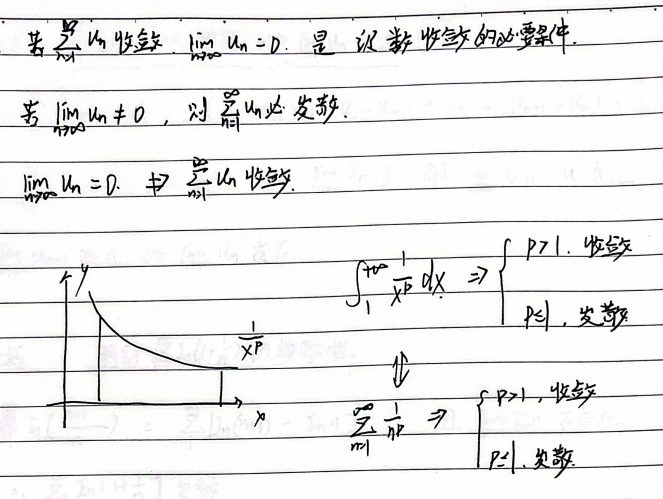
5.3 级数敛散性的判别方法

正项级数的判别方式 – 收敛原则

正项级数的判别方式 – 比较判别法

正项级数的判别方式 – 比较判别法的极限形式

正项级数的判别方式 – 比值判别法（达朗贝尔判别法）

正项级数的判别方式 – 根值判别法（柯西不等式）

正项级数的判别方式 – 积分判别法

5.4 交错级数及其敛散性判别

5.5 任意项级数及其敛散性判别（绝对值判别法）

绝对收敛、条件收敛的基本定义

几个注意点

5.6 抽象数列级数的判敛问题

5.7 幂级数概念

5.8 阿贝尔定理（区间端点处敛散性需要单独判断）

5.9 求收敛半径

5.10 收敛域求法

5.10.1 不缺项幂级数

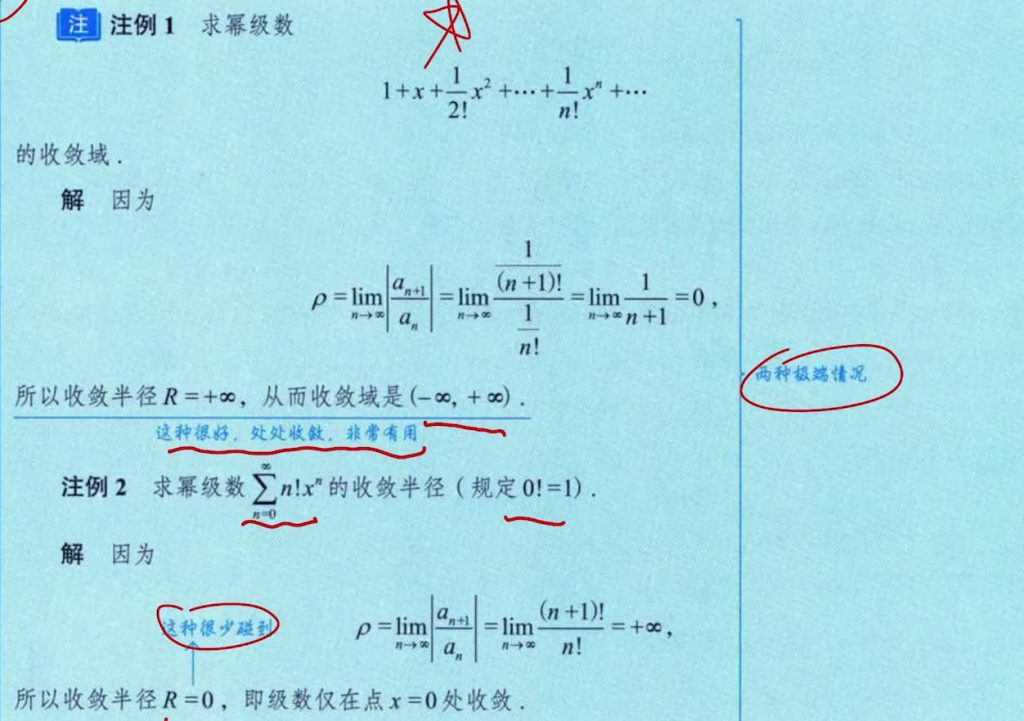
5.10.2 缺项幂级数和一般函数项级数（方法通用）

注意收敛区间和收敛域的区别

收敛区间（a，b）

单独讨论端点，确认收敛域

5.10.3 抽象型幂级数的收敛域

5.11 幂级数概念及运算法则

5.12 幂级数恒等变形方式

5.13幂级数的和函数性质

5.14 幂级数和函数的展开式

二、线性代数部分

三、概率论与数理统计部分

第一章 随机事件和概率

1.1 两个基本原理

1.2 排列、组合

1.3 随机试验

1.4 样本空间

1.5 随机事件及关系

随机事件、基本事件、事件发生、必然事件、不可能事件

随机事件的关系

随机事件关系应用

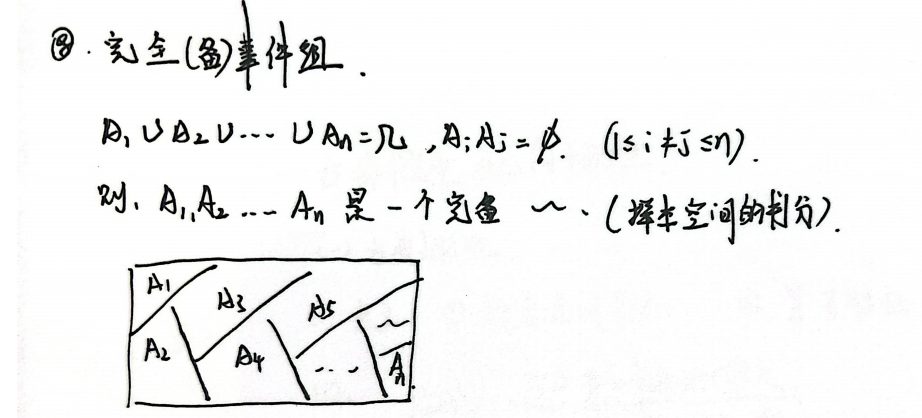
完备事件组

随机事件的运算律

1.6 古典概型与几何概型

古典概型

几何概型

1.7 概率的公理化定义及性质

定义

性质

1.8 条件概率及其性质

定义

性质

1.9 全概率公式

1.10 贝叶斯公式

基本思想及公式

推导

1.11 事件的独立性

两个事件的独立性定义

两事件独立的性质

三个事件的独立性

多个事件相互独立结论

1.12 n重伯努利概型及概率计算

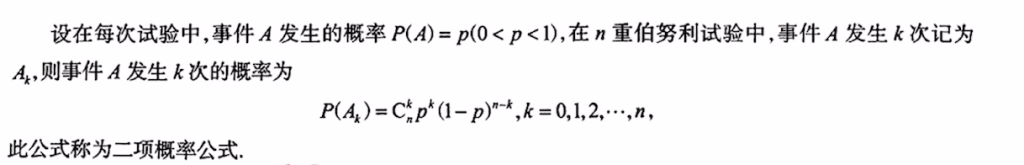
第二章 一维随机变量及其分布

2.1 随机变量的概念

随机变量的定义

随机变量的分类

2.2 随机变量分布函数

随机变量分布函数的定义

分布函数求各随机事件的概率

分布函数的性质

2.3 一维离散型随机变量

常见的离散分布

2.4 一维连续型随机变量及其概率分布

定义

概率密度函数的定义

2.5 常见的连续型分布（必考）

均匀分布

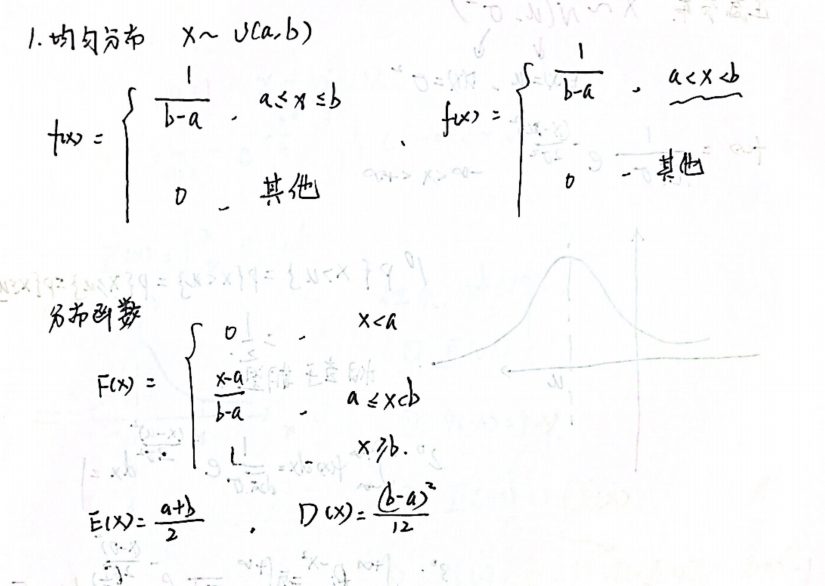
指数分布

正态分布（必考）

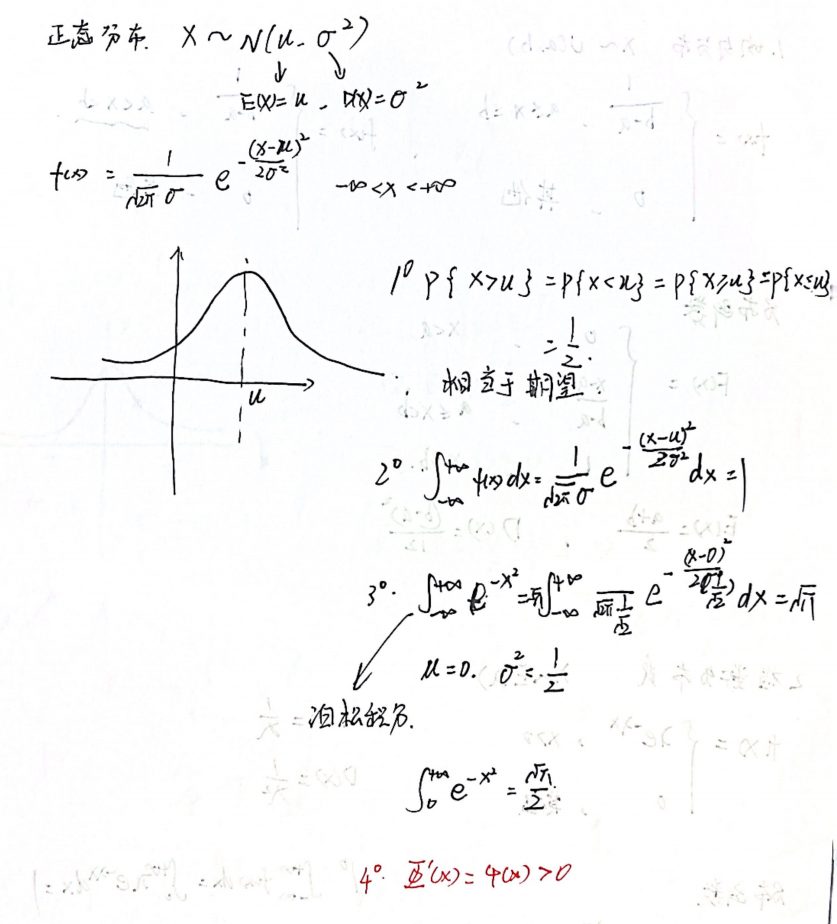
标准正态分布

正态分布标准化

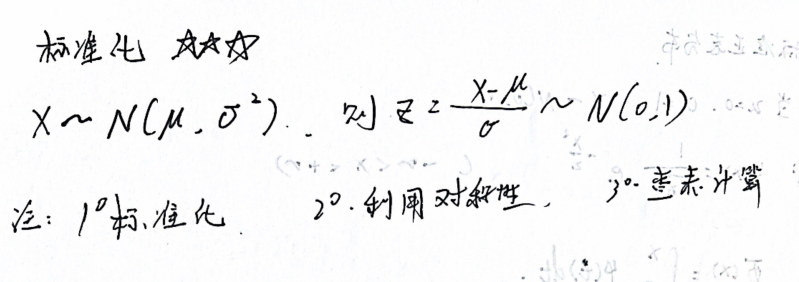
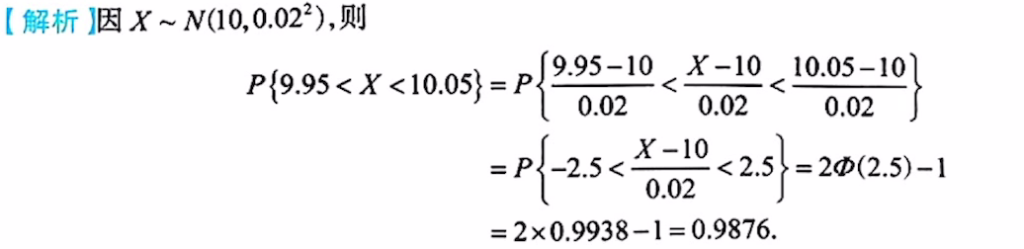
2.6 一维连续性随机变量函数的分布

一维离散型随机变量函数的分布

一维连续性随机变量的函数

第三章 多维随机变量及其分布

3.1 二维随机变量

二维随机变量联合分布函数的定义和性质

二维随机变量的边缘分布函数

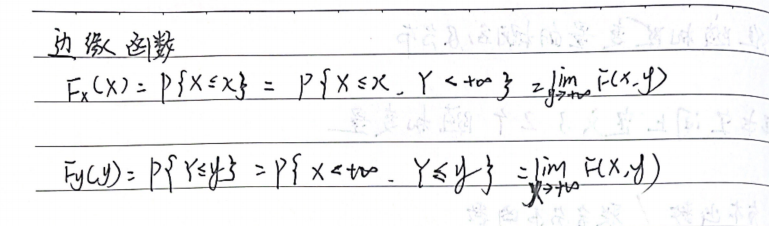
二维随机变量的边缘分布函数

3.2 二维离散型随机变量及其概率分布

二维离散型随机变量的定义

二维离散型随机变量的分布律

边缘分布律

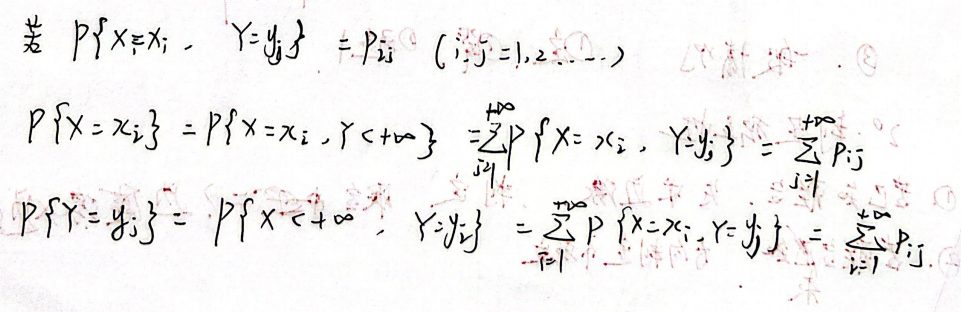
条件分布律

两个离散型随机变量函数的分布